Posterior contraction rate of sparse latent feature models with application to proteomics

Figures & data

Figure 1. An example of a tree structure $\mathcal{T}$, which is a directed graph with random variables at the nodes (marked as circles). Entries of the kth column of Z, $z_{jk}$'s, are at the leaves. The lengths of all edges of $\mathcal{T}$, $t_i$'s and ${\eta }_l$'s, are marked on the figure. In particular, ${\eta }_l$'s represent the lengths between each leaf ($z_{jk}$, shaded nodes) and its parent node (${\zeta }_l$, dotted nodes). The total edge lengths $S(\mathcal{T})$ is the summation of the lengths of all edges of $\mathcal{T}$. In this example, $S(\mathcal{T})=\sum _{1\le i\le 6}{t}_i+(2{\eta }_1+{\eta }_2+3{\eta }_3+{\eta }_4+4{\eta }_5+{\eta }_6)$. The condition in case (2) of Lemma 3.3 in Section 3 means $\underset{1\le l\le 6}{inf}{\eta }_l\ge {\eta }_0$ for some ${\eta }_0>0$.

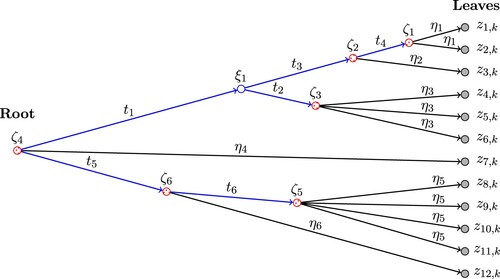
Table 1. Simulation results for different combinations of n and p.

$(n,p)$	p/n	$K_{sd}$	$\Vert Z{Z}^T-Z^{\ast }{Z}^{\ast T}{\Vert }_{sd}$	${ϵ}_{sd}$	$(\Vert Z{Z}^T-Z^{\ast }{Z}^{\ast T}\Vert /ϵ{)}_{sd}$
$(20,50)$	2.5	${13.550}_{2.385}$	${16.349}_{5.315}$	${125.191}_{6.627}$	${0.131}_{0.043}$
$(50,50)$	1	${10.700}_{0.791}$	$\phantom{1}{3.444}_{2.205}$	$\phantom{1}{79.178}_{4.191}$	${0.043}_{0.027}$
$(80,50)$	0.625	${10.300}_{0.564}$	$\phantom{1}{0.591}_{1.117}$	$\phantom{1}{62.596}_{3.313}$	${0.009}_{0.018}$
$(100,50)$	0.5	${10.275}_{0.506}$	$\phantom{1}{0.478}_{0.951}$	$\phantom{1}{55.987}_{2.964}$	${0.008}_{0.017}$
$(20,100)$	5	${12.650}_{1.718}$	${12.505}_{3.029}$	$\phantom{1}{92.532}_{7.750}$	${0.136}_{0.032}$
$(50,100)$	2	${10.750}_{0.776}$	$\phantom{1}{3.495}_{1.552}$	$\phantom{1}{58.522}_{4.901}$	${0.060}_{0.027}$
$(80,100)$	1.25	${10.275}_{0.506}$	$\phantom{1}{0.709}_{1.315}$	$\phantom{1}{46.266}_{3.875}$	${0.016}_{0.030}$
$(100,100)$	1	${10.250}_{0.494}$	$\phantom{1}{0.343}_{0.734}$	$\phantom{1}{41.382}_{3.466}$	${0.008}_{0.017}$
$(20,150)$	7.5	${12.600}_{2.073}$	$\phantom{1}{11.339}_{2.618}$	$\phantom{1}{84.131}_{5.881}$	${0.136}_{0.036}$
$(50,150)$	3	${10.675}_{0.797}$	$\phantom{1}{3.387}_{1.876}$	$\phantom{1}{53.209}_{3.719}$	${0.063}_{0.033}$
$(80,150)$	1.875	${10.282}_{0.456}$	$\phantom{1}{0.472}_{0.884}$	$\phantom{1}{42.065}_{2.940}$	${0.012}_{0.022}$
$(100,150)$	1.5	${10.250}_{0.439}$	$\phantom{1}{0.250}_{0.439}$	$\phantom{1}{37.624}_{2.630}$	${0.007}_{0.012}$

Note: The true $K^{\ast }=10$. Results are based on the sample values of K and Z from the 1000th MCMC iteration. The ϵ values are calculated based on the definition in Theorem 3.4. Entries in normal size and in the subscript (columns 3 and 4) are the averages and standard deviations over 40 independent simulation studies.

Figure 2. Simulation results for different combinations of n and p. Plot of $\Vert Z_n{Z}_n^T-Z_n^{\ast }{Z}_n^{\ast T}\Vert /{ϵ}_n$ versus n, where $\Vert Z_n{Z}_n^T-Z_n^{\ast }{Z}_n^{\ast T}\Vert$ is the spectral norm for the residual of the similarity matrix, and ${ϵ}_n$ is the posterior contraction rate defined in Theorem 3.4. The ratio converges to zero as n increases, demonstrating the theoretical results. The vertical error bars represent one standard error.

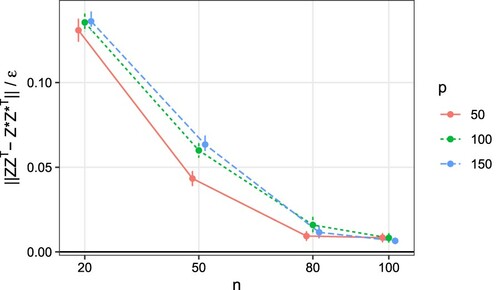
Table 2. Simulation results for different s.

s	s/p	$K_{sd}$	$\Vert Z{Z}^T-Z^{\ast }{Z}^{\ast T}{\Vert }_{sd}$
10	0.2	${10.225}_{0.480}$	${0.200}_{0.405}$
15	0.3	${10.100}_{0.304}$	${0.100}_{0.304}$
18	0.36	${10.225}_{0.423}$	${1.212}_{5.454}$
20	0.4	${10.275}_{0.554}$	${1.959}_{5.146}$
23	0.46	${10.850}_{0.802}$	${20.192}_{26.867}$
25	0.5	${11.150}_{0.736}$	${24.552}_{19.141}$

Note: The true $(n,p,K^{\ast })=(100,50,10)$. Results are based on the sample values of K and Z from the 1000th MCMC iteration. Entries in normal size and in the subscript (rows 3 and 4) are the averages and standard deviations over 40 independent simulation studies.

Figure 3. The inferred binary feature matrix $\hat{Z}$ for the TCGA RPPA dataset. The dataset consists of 100 patients, with 20 patients for each of the 5 cancer type, BRCA, DLBC, GBM, KIRC and LUAD. A shaded gray rectangle indicates the corresponding patient j possesses feature k, i.e., the corresponding matrix element ${\hat{Z}}_{jk}=1$. The columns are in descending order of the number of objects possessing each feature. The rows are reordered for better display.