Developing Students’ Intuition on the Impact of Correlated Outcomes

Figures & data

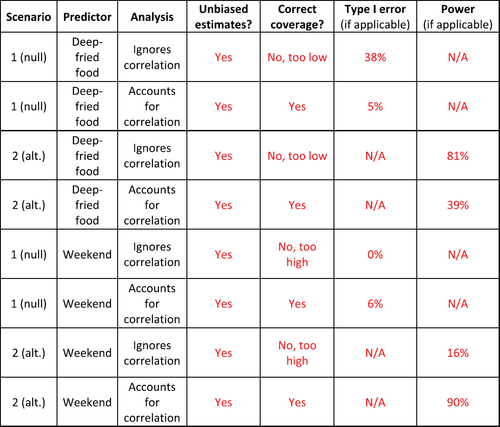
Fig. 1 An example to illustrate the impact of correlation on the variances of sums and differences. The pairs of heights from fathers and sons have a larger variance for their sums and a smaller variance for their differences than those from unrelated pairs.

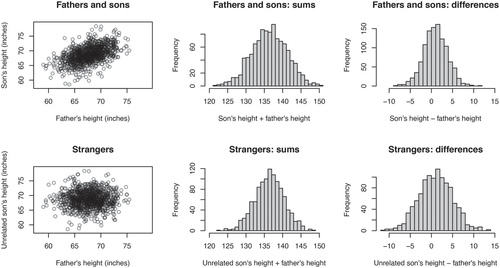
Fig. 2 A visual representation of the definition for sample covariance. Each data point (x_i , y_i ) has a corresponding shaded rectangle whose area is the deviation from the variables’ means, $(x_i-\overline{x})(y_i-\overline{y})$. Larger rectangles correspond to data points further from their means. Rectangles are shaded green when the variables “move together” (i.e., both values are larger or smaller than their respective means) and shaded red when they do not (e.g., one value is larger than its mean and the other is smaller). The sample covariance is the difference between the total area of the green rectangles and the red rectangles (divided by n – 1).

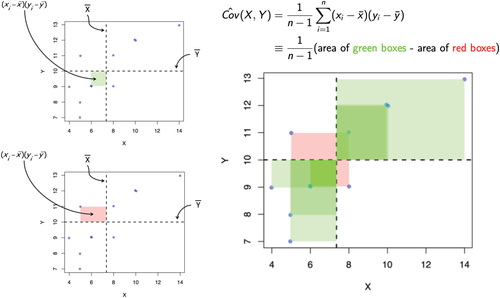
Fig. 3 A summary of how underestimating or overestimating the variance of the effect estimate $\widehat{\beta }$ due to ignoring correlated outcomes can lead to anti-conservative or conservative inference, respectively.

Fig. 4 Example results, corresponding to the results for the deep-fried food predictor under the null hypothesis when using an analysis approach that ignores correlation, for one of the eight settings that students investigate. The plots summarize the results from the analyses of the 1000 studies run for this setting. The left plot is a histogram of the 1000 point estimates ($\widehat{\beta }$’s), the middle plot shows 50 of the 1000 confidence intervals where the blue line indicates the truth, and the left plot shows a histogram of the 1000 p-values obtained.

Fig. 5 Results table for the activity with the solutions that students complete shown in red.

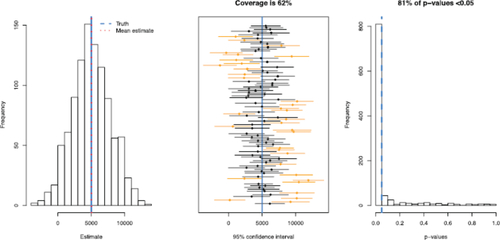
Fig. 6 Example dataset for a single replicate in “long” form with a single observation per row and the observations from a single cluster spanning multiple rows.

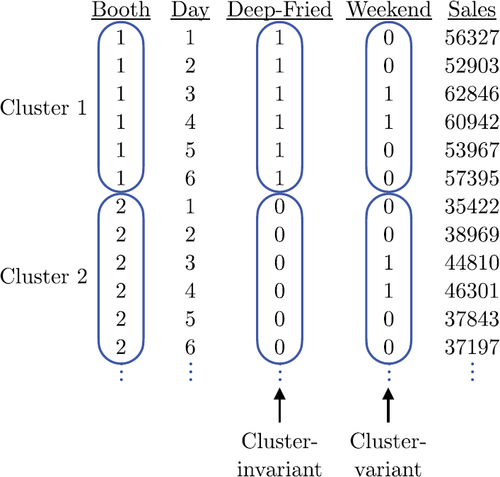
Fig. 7 A flowchart summarizing the implications of ignoring correlation between outcomes for predictors that vary or do not vary within cluster. For intuition about the second connection, have students recall the example about the variability of the sums and differences of father–son heights. For more detail about the third connection, see Figure 3.

Table 1 Comparison of the point estimates and standard errors (SEs) obtained for a correlated dataset using Gaussian generalized estimating equations (GEE) models with different working correlations and a naive linear regression model that assumes independent outcomes.

	${\widehat{\beta }}_0$ (SE)	${\widehat{\beta }}_1$ (SE)	${\widehat{\beta }}_2$ (SE)
GEE
(independence)	0.15328 (0.01323)	−0.00770 (0.00251)	−0.02980 (0.01300)
GEE
(exchangeable)	0.15328 (0.01323)	−0.00770 (0.00251)	−0.02980 (0.01300)
GEE (AR-1)	0.15628 (0.01364)	−0.00824 (0.00258)	−0.03083 (0.01289)
GEE
(unstructured)	0.15439 (0.01333)	−0.00754 (0.00252)	−0.03133 (0.01271)
Naive model	0.15328 (0.01123)	−0.00770 (0.00298)	−0.02980 (0.00867)

NOTE: The naive model overestimated the SE for ${\widehat{\beta }}_1$ since the corresponding covariate varied within clusters and underestimated the SE for ${\widehat{\beta }}_2$ since the corresponding covariate varied between clusters. Note that for this particular analysis, the data were balanced (i.e., the same number of observations per cluster) and complete (i.e., no missing data), thus, the results using an independence and exchangeable working correlation were exactly the same.

Table 2 Example questions and answers used in homework assignments, quizzes, and tests throughout the semester to reinforce students’ intuition about the impact of ignoring correlation between outcomes.

Sample questions	Sample answers
True or False: After analyzing longitudinal data using a GEE model, you find out that there are several pairs of siblings in your study, which examines an outcome thought to be impacted by genetic factors. Your original GEE results will still provide trustworthy inference since GEE uses sandwich variances that help when the variance structure is incorrectly specified.	False. GEE requires independent clusters (which would be violated by having siblings in your study) to obtain trustworthy inference.
Your collaborator fits a GLM model to this data and finds that the confidence interval for the intervention effect is narrower than the one you obtained using the GEE model. Seeing this, he insists that his analysis is preferable. In one to two sentences, provide a response to him.	The GLM model is inappropriate as it assumes independent outcomes. When our analysis ignores correlated outcomes, we will obtain too narrow of confidence intervals for cluster-invariant predictors (like intervention in this case), which results in an inflated Type I error rate.
How do the standard errors for the coefficients in your GLM model compare to the standard errors in the GEE models? Explain how this fits with what we have learned previously about the impact of ignoring correlated outcomes in analyses.	The standard errors for the variables that do not vary within cluster (i.e., intercept, treatment) are smaller in the GLM than the GEE models. In contrast, the standard errors for the variables that do vary within cluster (i.e., time, time by treatment interaction) are larger in the GLM than the GEE models. This fits with what we have learned: ignoring correlation will lead to overly narrow confidence intervals for between-cluster effects and overly wide confidence intervals for within-cluster effects.
Your collaborator performs a crossover study in which each subject receives the experimental treatment at one time point and the placebo at the other time point. He compares the outcomes between the experimental treatment and placebo using a two-sample t-test. The obtained p-value will be too _________ and the confidence interval will be too _________, which we call inference.	large / wide / conservative
True or False: Analyzing correlated outcomes as if they are independent always leads to obtaining too small of p-values.	False. Ignoring correlation can lead to too small or too large of p-values, depending on whether the covariate is cluster-invariant or cluster-variant.