Simulations and scaling of horizontal convection

Figures & data

Table 1. Experimental set-up for no-wind cases

	Ra	V (m^2 s^−1)	κ (m^2 s^−1)	A 0 (1 s^−1)	Number of grid points in y, z
NoWind1	10^6	1.2907×10^−2	1.2907×10^−8	0	256×128
NoWind2	10^7	4.082×10^−8	4.082×10^−4	0	256×128
NoWind3	10^8	1.2907×10^−8	1.2907×10^−4	0	512×256
NoWind4	10^9	4.082×10^−4	4.082×10^−5	0	512×256
NoWind5	10^10	1.2907×10^−4	1.2907×10^−5	0	800×512
NoWind6	10^11	4.082×10^−5	4.082×10^−6	0	1350×1350

Fig. 1.  Energetics at Ra = 10⁷ (top) and Ra = 10¹⁰ (bottom). Specifically, (a) evolution of the energy budget at Ra = 10⁷ with linear equation of state. At the later stages of the integration, the kinetic energy dissipation, ɛ, is equal to the conversion of potential energy to kinetic energy (C) which in turn is equal to the generation of potential energy by the thermodynamic forcing, P. (b) ɛ versus time for experiments with different equations of state at Ra = 10⁷, and the upper bounds established by Paparella and Young (2002) and Nycander (2010). (c) Same as (a) but at Ra = 10¹⁰. (d) Same as (b) but only for linear equation of state. In all panels, the time is scaled by the diffusion time, H ²/κ where H is the total depth of the domain and κ is the diffusivity used in the experiment.

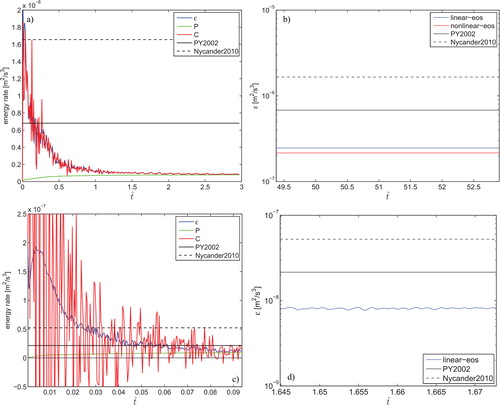
Fig. 2.  Time-averaged density field contours (left column) for and stream function (right column) for: (a) and (b) Ra = 10⁶; (c) and (d) Ra = 10⁷, (e) and (f) Ra = 10⁸. At these Rayleigh numbers, the flow is almost steady, and snapshots are very similar.

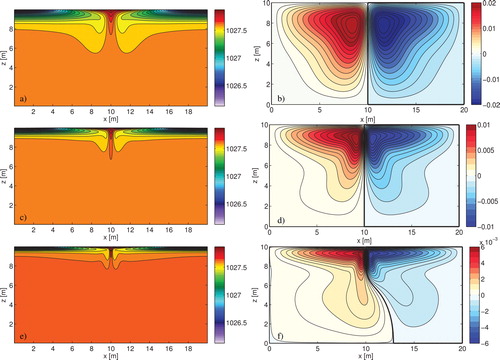
Fig. 3.  As for Fig. 2, but for Rayleigh numbers of, from the top: Ra = 10⁹, Ra = 10¹⁰, and Ra = 10¹¹. At Ra = 10¹⁰ and Ra = 10¹¹, the flow is unsteady.

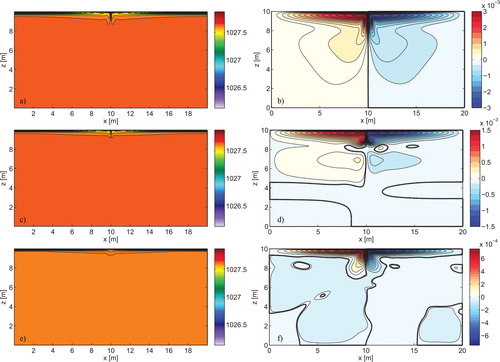
Fig. 4.  Snapshots of the density (left) and the stream function (right) fields of the Ra = 10¹⁰ experiment.

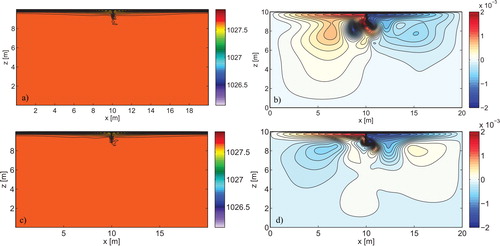
Fig. 5.  (a) Non-dimensional stream function () and dimensional stream function versus Rayleigh number, (b) Thermocline depth (h) versus Rayleigh number for no-wind experiments.

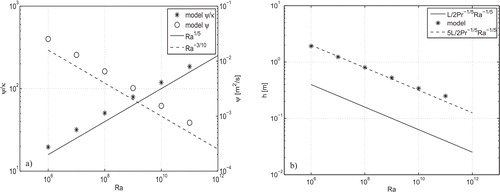
Fig. 6.  (a) The total kinetic energy of the flow for various values of the Rayleigh number is increased. Circles are the kinetic energy of the time-mean flow, and stars are the time-averaged kinetic energy of the total flow, including eddying terms. (b) Reynolds number, , as a function of Rayleigh number. (c) Total kinetic energy as a function of time for the Ra = 10⁹, 10¹⁰ and 10¹¹ cases. Time is scaled by the diffusion time, H ²/κ with κ the diffusivity at Ra = 10¹⁰.

Fig. 7.  (a) Mean dissipation rate (ɛ) and non-dimensional dissipation rate () versus Rayleigh number. (b) Buoyancy variance dissipation rate (χ) as a function of diffusivity, κ.

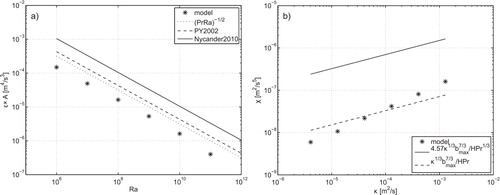
Fig. 8.  (a) Time-averaged density field contours (left column) for and stream function (right column) for: (a) and (b) at the top and at the bottom of the tank; (c) and (d) at the top and at the bottom of the tank.

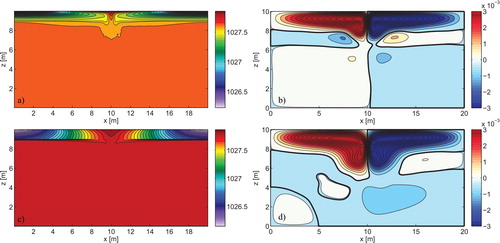
Fig. 9.  Time-averaged stream function fields at Ra = 10⁷ for (a) linear equation of state, (c) nonlinear equation of state. Time-averaged density fields at Ra = 10⁷ for (b) linear equation of state, (d) nonlinear equation of state.

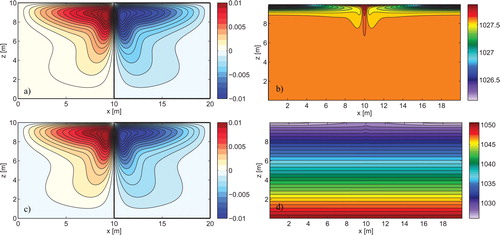
Table 2. Experimental set-up for wind cases

	Ra	A 0 (1 s^−1)	ω (1 s^−1)
Wind1	10^9	0.0256	N 0=0.04
Wind2	10^9	0.0256	5N 0=0.2
Wind3	10^9	0.0256	N 0/5 = 0.008
Wind4	10^9	0.16	N 0=0.04
Wind5	10^9	0.16	5N 0=0.2
Wind6	10^9	0.16	N 0/5 = 0.008
Wind7	10^9	0.432	N 0=0.04
Wind8	10^9	0.432	5N 0=0.2
Wind9	10^9	0.432	N 0/5 = 0.008
Wind10	10^9	1.0	N 0=0.04
Wind11	10^9	1.0	5N 0=0.2
Wind12	10^9	1.0	N 0/5 = 0.008

Fig. 10.  Time-averaged density field contours for (a) A ₀=0.16, ω=0.008; (c) A ₀=0.16, ω=0.04 and (e) A ₀=0.16, ω=0.2. Time-averaged stream function contours for (b) A ₀=0.16, ω=0.008; (d) A ₀=0.16, ω=0.04 and (f) A ₀=0.16, ω=0.2.

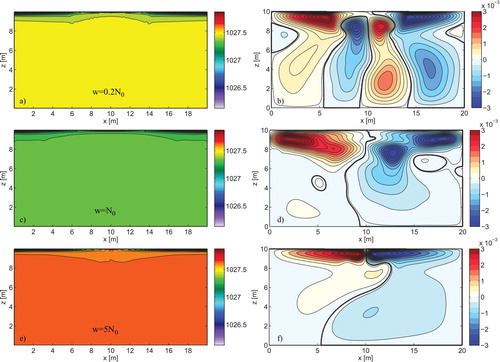
Fig. 11.  Time-averaged density field contours for (a) A ₀=0.4213, ω=0.008; (c) A ₀=0.4213, ω=0.04 and (e) A ₀=0.4213, ω=0.2. Time-averaged stream function contours for (b) A ₀=0.4213, ω=0.008; (d) A ₀=0.4213, ω=0.04 and (f) A ₀=0.4213, ω=0.2.

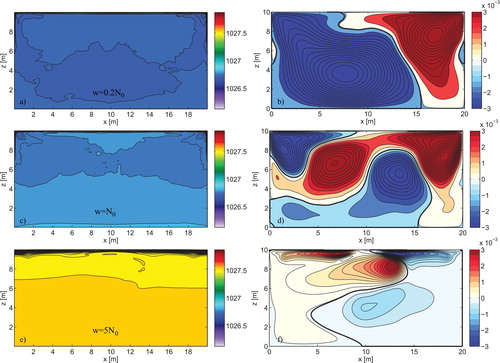
Fig. 12.  Spatial and time-averaged buoyancy profile for the no-wind case (solid line) and wind case (dashed line) with A ₀=0.16 and ω=N ₀, away from the sinking region. The straight vertical lines are the values at the bottom of the domain.

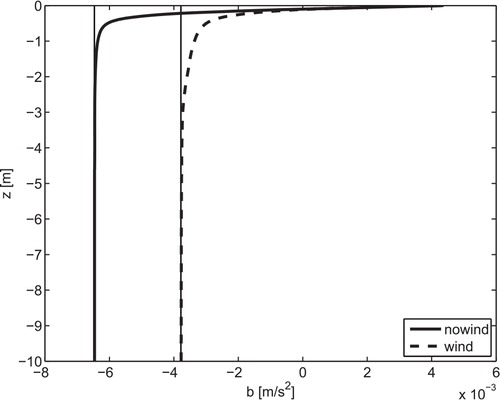
Fig. 13.  (a) Mean dissipation rate (ɛ) versus strength of the wind. (b) Buoyancy variance dissipation rate (χ) as a function of strength of the wind. (c) Maximum stream function versus strength of the wind.

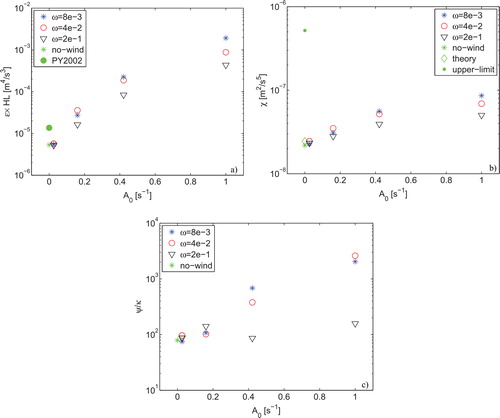
Fig. 14.  (a) Available potential energy as a function of diffusivity, κ. (b) Available potential energy versus strength of the wind.

Paparella F. Young W. R. Horizontal convection is non-turbulent. J. Fluid Mech. 2002; 466: 205–214. 10.3402/tellusa.v64i0.18377.

 Web of Science ®Google Scholar

Nycander J. Horizontal convection with a non-linear equation of state: generalization of a theorem of Paparella and Young. Tellus A. 2010; 62: 134–137. 10.3402/tellusa.v64i0.18377.

 Google Scholar