Abstract
A -ranking of a directed graph
is a labeling of the vertex set of
with
positive integers such that every directed path connecting two vertices with the same label includes a vertex with a larger label in between. The rank number of
is defined to be the smallest
such that
has a
-ranking. We find the largest possible directed graph that can be obtained from a directed path or a directed cycle by attaching new edges to the vertices such that the new graphs have the same rank number as the original graphs. The adjacency matrix of the resulting graph is embedded in the Sierpiński triangle.
We present a connection between the number of edges that can be added to paths and the Stirling numbers of the second kind. These results are generalized to create directed graphs which are unions of directed paths and directed cycles that maintain the rank number of a base graph of a directed path or a directed cycle.
1 Introduction
A vertex coloring of a directed graph is a labeling of its vertices so that no two adjacent vertices receive the same label. In a directed path, edges are oriented in the same direction. A -ranking of a directed graph is a labeling of the vertex set with
positive integers such that for every directed path connecting two vertices with the same label there is a vertex with a larger label in between. A ranking is minimal if the reduction of any label violates the ranking property. The rank number
of a directed graph
is the smallest
such that
has a minimal
-ranking.
Table
It is known that the rank number of a graph may increase just by adding a new edge, even if the new edge and
share vertices. This raises the question “what is the maximum size of a directed graph that satisfies the property that its rank number is equal to the rank number of its largest directed subpath?” Flórez and Narayan [Citation1,Citation2] found results related to this question; however, the problem is still open. We believe that studying particular cases will lead to a better understanding of the problem and potential solutions.
In this paper we study the necessary and sufficient conditions for the largest possible directed graph that can be obtained by attaching edges to either a directed path or directed cycle without changing the rank number and the number of vertices. In [Citation1] there is a solution for the undirected case. Here, we analyze cases for which the new directed graph keeps the rank number of the original graph. The maximum number of edges in such graphs is described as well as which edges are present in the graphs.
We build families of directed graphs by adding directed edges (called admissible) to a directed path (called the base). Those families satisfy the condition that the graphs are maximal graphs with the property that the rank number of each graph equals the rank number of the base directed path. The graphs of the first two families described were constructed recursively by adding all admissible edges (without increasing the number of vertices) to a base directed path. The same idea is extended to directed cycles.
We generalize the concept developed to build the first four families above to other maximal families of graphs preserving the rank number of the base directed path by adding admissible directed paths and directed cycles to a base directed path or directed cycle.
The number of edges and the number of admissible edges of the graphs in the first four families are counted using known numerical sequences. We prove, using the recursive construction, that the maximum number of edges in some of those families of graphs is given by a Stirling number of the second kind.
For those who are interested in computational matters, we provide algorithms, some of which are given in terms of adjacency matrices. We found an interesting connection between one of the adjacency matrices and the Sierpiński triangle. The adjacency matrix of the first graph found in this paper embeds naturally in the Sierpiński sieve triangle.
2 Preliminary concepts
In this section we review some known concepts and results, introduce new definitions, and give a proof for a lemma.
Let be a set of vertices of a directed graph. An edge (arc) with vertices
,
, with orientation
is denoted by
or by
, and the edge with orientation
is denoted by
or by
. A directed path with vertices
is denoted by
if its edges are of the form
. A directed cycle with vertices
is denoted by
if its edges are of the form
.
Let be a finite directed graph with vertex set
. A
-ranking of
is a labeling (or coloring) of
with
positive integers such that every directed path that connects two vertices of the same label (color) contains a vertex of a larger label (color). Thus, a labeling function
is a vertex
-ranking of
if for all
such that
and
, then every directed path connecting
and
contains a vertex
such that
. Like the chromatic number, the rank number of a graph
is defined to be the smallest
such that
has a minimal
-ranking; it is denoted by
.
Let and
be directed graphs with
and
. We say that a directed edge
is admissible for
if
, and
is forbidden for
if
.
We distinguish two types of admissible edges. A directed edge is admissible of type I for
if
and the edges in the edge set of
have the same direction. A directed edge
is admissible of type II if
and the edges in the edge set of
have opposite direction. Note that admissible edges of type II allow for edges with opposite directions between two vertices.
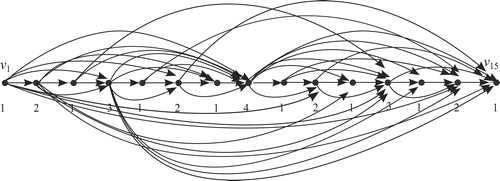
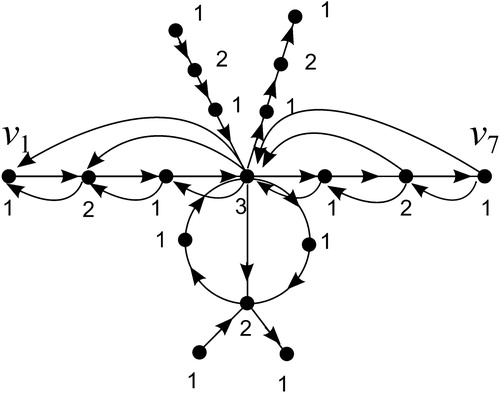
For example, shows the graph where
is the graph formed with all admissible edges of type I for
. In we show the graph
where
is the graph formed with all admissible edges of type II for
. Since
gives rise to both graphs
and
, they have the same set of vertices
, where
is leftmost vertex and
is the rightmost vertex. The numbers on the graphs represent the labelings. That is,
The largest label in is 4. So, 4 is the rank number of the graphs
,
, and
. Thus,
.
Bodlaender et al. [Citation3] determined the rank number of a path to be
. Bruoth and M. Horňák [Citation4] found a similar value,
, for
. It is easy to see that these two properties are true for both
and
, respectively. A minimal ranking for these two types of graphs can be obtained by labeling the vertices
with
where
is the highest power of 2 that divides
. If
, then the minimal ranking of
is unique. If
, then the minimal ranking of
is unique. These two rankings are called the standard minimal rankings. The following lemma summarizes these properties.
Lemma 1
[Citation3,Citation4]
If is any of the graphs
or
, then
has a unique minimal ranking and
We now give some definitions that are going to be used in the results that follow. Let be a directed graph with
as its
-ranking function. We define
and use
to denote the set of all components of
where
.
Let with
, and let
with
. We define the direct sum graph of type I recursively, denoted by
, as the graph with vertex set
where
and
is the graph obtained from a copy of
by relabeling the vertices of
as follows
for
. That is,
. The edge set of
is
where
(1) For example,
is depicted in .
We use to denote the graph with the set of vertices equal to the set of vertices of
and the set of edges defined by
(2)
3 Admissible edges of type I
This section proves several properties of the direct sum graph of type I. Assume that all admissible edges and direct sum graphs considered throughout this section are of type I. The path gives rise to the direct sum graph
, and they both preserve many properties, including the symmetry described below. We prove that
is the largest graph that shares with
the set of vertices, the orientation, the
-rank number, and the same vertex labeling when the labeling is minimum. Note that
is
. We prove that
is the set of admissible edges for
.
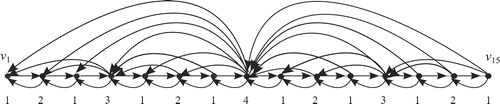
Consider the symmetry seen on the graph , (see ). This symmetry occurs in general in
(see Section 4). However, the symmetry in the graph
is not obvious but does exist (see ). In Section 5, we give a recursive algorithm to build the adjacency matrix that represents
. The adjacency matrix given by Algorithm 1 is symmetric with respect to the antidiagonal (for example, see the matrices in ). This symmetry can be predicted based on how the direct sum graph
is defined.
Table 1 The adjacency matrices for the direct sum graphs of type I with  and
and  vertices, respectively.
vertices, respectively.
Recall that the Stirling numbers of the second kind count the ways to divide a set of
objects into
nonempty subsets where
. We are interested in the following Stirling numbers,
and
. We prove that the number of edges of
and the number of admissible edges for
can be described by Stirling numbers of the second kind.
Proposition 2
If and
is the direct sum graph of type I, then
| 1. |
| ||||
| 2. | the total number of edges in | ||||
| 3. | an edge | ||||
| 4. | the total number of admissible edges of type I for | ||||
Proof
Part 1: The proof is inductive. Let be the statement:
for
and that
and
have the same minimal labeling. For this proof we assume that the labeling of
is minimal.
The proof of is straightforward from the definition of
. We now suppose that
is true for some fixed
with
. Thus,
is true for some fixed
with
. (We prove
is true.)
Consider the graphs and
, where
. From the inductive hypothesis and Lemma 1 we know that both graphs have
vertices with the same labeling and that this labeling is minimal and unique. From the definition of
we know that its vertices are
from left to right. To label
, we define
as follows: the function
keeps the same labels from
for
and from
for
and
since
needs a new label. The function
is a well defined labeling for
since
preserves a good labeling for the edges
Part 2: Let the total number of edges in be denoted by
. From the definition of edges of
it is easy to see that,
We prove by induction that the number of edges in is given by
. Let
be the statement:
for
.
We prove . From definition of
, we have
. We now suppose that
is true for some fixed
with
. Therefore,
is true for some fixed
with
. Thus,
is true. (We prove
is true.)
Since , we have that
which shows that
holds. Note that
is twice the Stirling number of second kind. That is,
has
edges.
Part 3: Suppose that . Then by the definition of
in (Equation2
(2) ) and part 1 of this proposition,
is an admissible edge for
.
Now suppose that is an admissible edge for
. We prove that
. Let
and
be the vertices of
with
.
Case 1. Suppose that and
are in the same component
of
. We prove the case in which
and since the proof of the case in which
is similar, we omit it. Recall that
has
vertices and that
is the largest label in
. Since
has the largest label in the component, it corresponds to the vertex in position
. Then by the definition of
, the edge
belongs to
as defined in (Equation1
(1) ). Thus,
.
Case 2. Suppose that and
where
and
are distinct components of
. Let
be a vertex in
with
, where
is the largest label in
.
Subcase 1. Suppose that . Note that if
or if
is located in
in a position to the left of
, then
gives rise to a path connecting
and
which does not contain a larger label in between
and
. That is a contradiction because
is an admissible edge for
. Thus,
must be located in
in a position to the right of
. This implies that
satisfies the condition described in the last set in the definition of
in (Equation1
(1) ).
Subcase 2. Suppose that . Note that if
or if
is located in
in a position to the right of
, then
gives rise to a path connecting
and
which does not contain a larger label in between
and
. That is a contradiction because
is an admissible edge for
. Thus,
must be located in
in a position to the left of
. This implies that
satisfies the condition described in the last set in the definition of
in (Equation1
(1) ).
Part 4: It is easy to see that has
edges, which can be rewritten as
. From part 3 of this proposition we know that the set of admissible edges for
is
. Therefore, the total number of admissible edges is the number of edges in
minus the number of edges in
which is
. □
4 Admissible edges of type II
This section discusses the admissible edges of type II for using the direct sum graph of type II defined below. Throughout this section, it can be assumed that all admissible edges and direct sum graphs are of type II. We prove that the direct sum graph is a maximum graph such that
and
have the same set of vertices,
-rank number, and vertex labeling when the labeling is minimum. The symmetry of
is straightforward, and an example can be seen in . Section 5 gives a recursive algorithm for the adjacency matrix for
. The symmetry found in
can be clearly seen in the adjacency matrix. It is also anti-diagonal symmetry.
We first discuss several necessary definitions. Let with vertices
and edges
, and let
with vertices
and edges
. We define the direct sum graph of type II recursively, denoted by
, as the graph with vertex set
where
and
is the graph obtained from a copy of
by relabeling the vertices of
as follows
for
. That is,
. The edge set of
is
where
(3) For example,
is depicted in .
We use to denote the graph with the set of vertices equal to the set of vertices of
and the set of edges defined by
(4)
Note that when the direction is removed from the edges in this construction, the resulting graph is the graph found in [Citation1] for the undirected case. Also note that this construction of is not unique. That is, there is more than one way to add admissible edges of type II to
to create a graph with the maximum number of these admissible edges as possible while maintaining the rank number.
The numerical sequences in Proposition 3 parts (2) and (4) are in Sloane [Citation5] at http://oeis.org/A058922 and http://oeis.org/A036799, respectively.
Proposition 3
If and
is the direct sum graph of type II, then
| 1. |
| ||||
| 2. | the total number of edges in | ||||
| 3. | an edge | ||||
| 4. | the total number of admissible edges of type II for | ||||
Proof
Part 1: We prove this part by induction. Let be the statement:
for
and that
and
have the same minimal labeling. For this proof suppose that the labeling of
is minimal.
The proof of is straightforward from the definition of
. Suppose that
is true for some fixed
with
. That is, suppose that
is true for some fixed
with
, and we prove
is also true.
Consider the graphs and
. From the inductive hypothesis and Lemma 1 we know that both graphs have
vertices with the same labeling and that it is minimal and unique. From the definition of
we know that its vertices are
from left to right. To label
, we define
as follows: the function
keeps the same labels from
for
and from
for
and
since
needs a new label. The function
is a well-defined labeling for
since
preserves a proper labeling for the edges
Part 2: Let the total number of edges in be denoted by
. From the definition of edges of
it is easy to see that,
We prove by induction that the number of edges in is given by
. Let
be the statement:
for
.
We prove . It is easy to see, from definition of
, that
. Suppose that
is true for some fix
with
. That is, suppose that
for some fix
with
and we prove
. Since
, we have that
Thus,
has
edges.
Part 3: Suppose that . Then by the definition of
and part 1 of this proposition,
is an admissible edge for
.
Now suppose that is an admissible edge for
. We prove that
by induction. Let
be the statement: if
is admissible in
, then
for
.
We prove . Let
be admissible in
. Then either
is in
or is
. The edge
leads to a contradiction since
violates a proper labeling. Therefore, if
is admissible in
, then
, and thus
.
Suppose that is true for some fixed
with
. Suppose that
is admissible in
with
and
as endpoints such that
.
Case 1. Suppose that and
are in the same component
of
. Then
has the largest label in
and is in position
. Thus,
as defined in (Equation3
(3) ) and
.
Case 2. Suppose that and
where
and
are distinct components of
. Let
such that
. The edge
gives rise to a path connecting
and
which does not contain a larger label in between
and
since each component contains all dual direction edges on the path. Such a path contradicts
being admissible in
. Therefore,
is admissible in
if and only if
.
Part 4: It is easy to see that has
edges. From part 3 of this proposition we know that set of admissible edges for
is
. Therefore, the total number of admissible edges is the number of edges in
minus the number of edges in
which is
. □
5 Adjacency matrices of  and
and 
In this section we give recursive algorithms that highlight the symmetric structure of the graphs and
. The algorithms are based on block-recursive adjacency matrices for direct sum graphs of type I and II. The matrices present symmetry with respect to the antidiagonal rather than the main diagonal (see for example and ).
Table 2 The adjacency matrices for the direct sum graphs of type II with  and
and  vertices, respectively.
vertices, respectively.
In we show the matrices and
that represent direct sum graphs of type I. We observe that
forms three blocks within
. Similarly,
will contain three blocks of
and so on. As mentioned previously, this symmetry is not obvious from looking at the corresponding graph, such as in . The component symmetry of direct sum graphs of type II is clear from a graph, such as in , but the fact that it is antidiagonal symmetry is obvious in the adjacency matrix found in . It should be clear that matrices for direct sum graphs of type I have the same block-recursive structure as matrices for direct sum graphs of type II, but the contents of the blocks are different.
In Algorithm 1, denotes a
matrix. We use
in this manner because it simplifies our description of the recursion. We denote by
the vector of length
where all entries are 1 and the transpose of this vector is denoted by
. We denote by
the
matrix where all its entries are zero. We divide matrix
into blocks with the layout shown in Algorithm 1. With this example in mind, our algorithm for constructing a matrix
follows. Note that
and 10 are not defined.
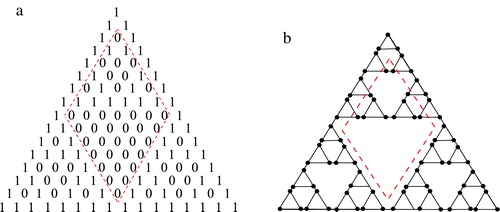
We observe, from the recursive definition of the graph , that the adjacency matrix of
embeds in the Sierpiński sieve triangle. For example, shows
embedded in the corresponding triangle. The entries of
are within the region bounded by the dashed diamond shape in part (a). Thus, the entries on the main diagonal of
correspond to the entries on line nine of the Sierpiński sieve triangle (which is row eight within the diamond). The entries on the super diagonal of
correspond to the entries on line eight of the Sierpiński sieve triangle (which is row seven within the diamond). The entries on the subdiagonal of
correspond to the entries on line 10 of the Sierpiński sieve triangle (which is row nine within the diamond) and so on. Thus, the entry
of
is given by
. Due to this embedding,
should be called the directed Sierpiński graph. In fact, because of this embedding, we can use any number of algorithms to construct
and the corresponding graphs. For related graphs, see for example the undirected Pascal graphs defined by Deo and Quinn [Citation6]. The undirected Sierpiński graph (or Hanoi graph) is represented in part (b) (see for example Romik [Citation7]).
One motivation for Deo and Quinn [Citation6] in describing undirected Pascal graphs was to define bidirectional computer network topologies with certain connectivity and cohesion constraints. It should be obvious how the incidence matrix of a type I graph embeds in an undirected Pascal graph—replacing by zero all nonzero entries that are below the main diagonal of the adjacency matrix of an undirected Pascal graph. Modern networks enable roles, communication, protocols, or permissions for which operations on distributed systems are asymmetric. Our directed graphs share some of the properties of Pascal graphs and may be useful in defining asymmetric computer networks with guaranteed properties.
In describing Algorithm 2, we use ,
and
to avoid confusion with Algorithm 1. We use
to denote a
matrix. As with
above, we use
in this manner because it simplifies our description of the recursion. We denote by
the vector of length
where all entries are 1. We denote by
the
matrix where all its entries are zero. We denote by
a single-entry column vector of length
where the last element is 1 and all others are 0 and by
a single-entry row vector where the first element is 1 and all others are 0. We divide matrix
into blocks with the layout shown in Algorithm 2. For example, in , we show the matrices
and
.
Our algorithm for constructing follows. As with
,
and 10 are not defined.
6 Admissible edges for a directed cycle
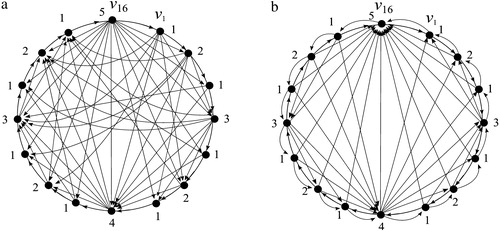
In this section we use the results from previous sections to find the admissible edges of type I and type II for and prove similar results. part (a) shows
with the admissible edges of type I. The number of edges in this graph is 65 and the number of admissible edges is 50. part (b) shows
with the admissible edges of type II. The number of edges in this graph is 65 and the number of admissible edges is 49. The number of admissible edges and the number of edges of the new graph are given by known numerical sequences. One of these sequences is the Stirling numbers. In both parts the rank number is equal to the rank number of
.
We recall that is the set of vertices of
, and that
is the set of vertices of
. We define
(5) where
is the set of admissible edges of type I for
(see (Equation2
(2) )). We now define
(6) where
is the set of admissible edges of type II for
(see (Equation4
(4) )).
We use and
to mean the graphs
and
, respectively. The numerical sequences in Proposition 4 parts (3), (4) and (6) are in Sloane [Citation5] at http://oeis.org/A001047, http://oeis.org/A002064 (called Cullen numbers), and http://oeis.org/A048495, respectively.
Proposition 4
If and
with
, then
| 1. | the set | ||||
| 2. | the set | ||||
| 3. | the total number of edges in | ||||
| 4. | the total number of edges in | ||||
| 5. | the total number of admissible edges of type I for | ||||
| 6. | the total number of admissible edges of type II for | ||||
Proof
We prove parts 1, 3, and 5. The proofs for part 2, 4, and 6 are similar, respectively, and we omit them. We assume all admissible edges are of type I throughout this proof.
Part 1: For the proof of necessity, it is easy to see that if is not a set of admissible edges, then this set contains a forbidden edge; therefore the rank number of
is different than the rank number of
. That is a contradiction.
We now prove sufficiency. From Lemma 1 we know that and that the minimal ranking is unique. Suppose that
is the ranking function of
. So,
.
Let and
be two edges of
and let
be subgraph of
formed by all edges of
that have vertices in
. That is,
and
is the set of vertices of
. Then by Proposition 4, we have
is a set of admissible edges for the graph
if and only if
. The vertices of
have the same labels as the vertices
.
We now prove that . Let
be an edge in
. That is,
Therefore, the vertices of
are
and
for some
. From definition of the labeling function
we know that
and
. We do not create any new paths in
connecting vertices with label
. This implies that the number of labels does not increase. This proves part 1.
Part 3: We consider the sets of edges and
defined as follows:
The cardinality of
is
. From Proposition 2 part 1 we know that all admissible edges for
are also admissible for
. Therefore, the maximum number of edges that can be added to
without changing its rank number is equal to maximum number of edges that can be added to
plus all edges in
. Thus, the total number of edges in
is equal to the number of admissible edges for
and the number of edges in
, plus the number of edges in
. Therefore, the number of edges in
is
.
Part 5: This proof is straightforward by counting the number of edges that are admissible for and adding the number of edges in
. □
Corollary 5
The graphs ,
,
,
have unique minimal rankings.
7 Admissible graphs for directed paths and cycles
In this section, we explore constructing new graphs by attaching directed paths and directed cycles to the direct sum graphs and the omega graphs built in the previous sections. We give algorithms for labeling the new resulting graphs. The algorithms keep the same rank number as the original graph. Thus, the rank number of the graphs constructed here is either the rank number of or of
.
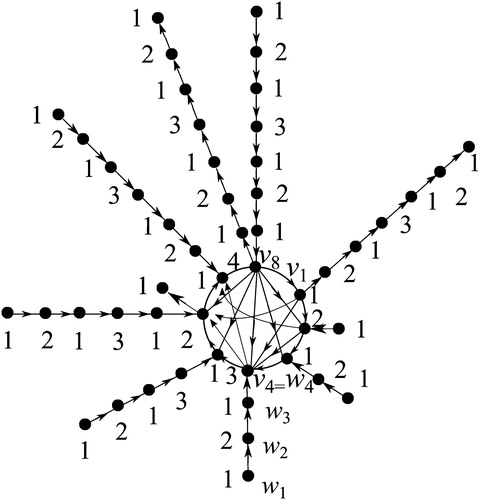
Finding the rank number of a given graph is a hard problem, even for simple graphs. In the previous sections, we took a known graph with known rank number, and we built a new graph that preserves the rank number and as well the set of vertices. In this section, we explore the same idea, but without preserving the set of vertices. Thus, we give some results on how to build new graphs from a base graph such that the new graph is larger than the original in terms of the number of vertices and preserves the rank number of the base graph.
Recall from Section 2 that or
have vertex sets
and
, respectively. We construct a new graph by attaching a directed path or a directed cycle to the vertex
for some
. Let
be the edges of a directed path of length
that is attached to
or
at the vertex
. The path is denoted by
if its edges are directed as
, and the path is denoted by
if its edges are directed as
. Notice that the edges of
and
are oriented as defined in Section 2.
From Sections 3 and 4 we know that and
with vertices
. We also know that
and
with vertices
where
is as in (Equation5
(5) ) and
is as in (Equation6
(6) ).
We say that a directed graph is admissible for a directed graph
if
, and
is forbidden for
if
. As an example of these admissible graphs and Lemma 6, see .
Lemma 6
If is either
or
, and
is either
or
, then
| 1. | the path | ||||
| 2. | the path | ||||
| 3. | the path | ||||
| 4. | the path | ||||
Proof
We prove parts 1 and 2. Parts 3 and 4 are similar, and we omit the proofs. For both parts 1 and 2, we prove the case . Since the case
is similar, it is omitted. We recall that
is the set of vertices of
and that the edges of
are directed as
for
.
Part 1. Suppose that is set of vertices of
for some fixed
where
is the path attached to the vertex
with edges directed as
.
Corollary 5 guarantees that has a unique minimal ranking. Let a minimal ranking function be
. Since
, we can label the vertices
with the labels given by the ranking function
without increasing the rank number of the new graph. Algorithm 3 allows us to do it. (See for example .)
Using Algorithm 3 we obtain Therefore, we have a ranking function
that labels all vertices of
without increasing the rank number. This proves that
.
Part 2. Suppose that is the set of vertices of
for some fixed
where
is the path attached to the vertex
with edges directed as
.
Corollary 5 guarantees that has a unique minimal ranking. Let a minimal ranking function be
. Since
, we can label the vertices of
with the labels given by the ranking function
. This labeling will not increase the rank number of the new graph. Algorithm 4 allows us to do it. (See for example .)
Using Algorithm 4 we obtain Therefore, we have a ranking function
that labels all vertices of
without increasing the rank number. That is,
. □
Proposition 7
If is either
or
, and
is either
or
, then
| 1. |
| ||||
| 2. |
| ||||
Proof
We prove part 1 for the case . The other case where
and part 2 are similar and thus omitted. From Lemma 6 part 1 we know that
. Let
be the minimal ranking of
. Using Algorithms 3 and 4 developed in the proof of Lemma 6, we define a ranking function
that labels all vertices of all paths of the form of
or of the form
attached to
. That is,
is the function defined by Algorithm 3 if the path is of the form
and
is the function defined by Algorithm 4 if the path is of the form
. From those algorithms it is easy to see that
.
Let be the function defined as
where
From the definition of
and
it is easy to see that
for
.
We now prove that is a ranking function of
. That is, we want to prove that given any two vertices in
with the same label, every directed path connecting those two vertices has a vertex with larger label. We prove it by contradiction. Suppose that there are two vertices
connected by a directed path
with
and for every other vertex
, we have
.
Let be the set of vertices of
, where
are vertices in
and
are vertices in
. Notice that
and
may be equal to one and that
and
may be equal. We suppose that the edges of
are of the form
,
, and
.
From Algorithm 3 in the proof of Lemma 6, we know that for
, and from Algorithm 4 we know that
for
. These imply that there exists a path
with vertices
in
satisfying that
and
for
. That is contradiction because
is a ranking function of
and
. This proves that
is a ranking function for
. The definition of
tells us that
for
. Thus,
. This proves part 1 with
. □
Recall that with
for
is the binary representation of a positive integer
if
. We define
as
if
is the rightmost nonzero entry of the binary representation of
. Flórez and Narayan [Citation1] proved that if
is a vertex of
in position
, then
where
is the ranking function of
. The same result extends naturally to directed paths.
Let be a subgraph of a graph
. A vertex of attachment of
in
is a vertex of
that is incident with some edge of
that is not an edge of
(for this definition see [Citation8] page 11 section I.4).
Let be either
or
with vertices
and let
be either
or
. We define
for some
.
Let Notice that
has exactly one vertex of attachment in
which is given by
. As an example of this graph and Proposition 8, see .
Let be the graph formed by
and the union of a set of graphs
for
, where
is an index set, such that the graphs
and
intersect exactly in the vertex
. That is,
has exactly one vertex of attachment
. Theorem 9 proves that
generalizes Lemma 6 and Propositions 7 and 8.
Proposition 8
If for each the set
is the maximum set of vertices of attachment of
in
, then
.
Proof
From Proposition 7, we know that where
for some
. From the definition of
we can see that
. Note that
and that every other vertex of
has label less than
. So, attaching
to
does not increase the rank number of
. Since this argument is true for every
, it proves that
. □
Theorem 9
Let be the vertex of attachment of
in
for
in an index set
and some
. Suppose that
. If there is a ranking function
of
such that
, then
.
Proof
Since the vertex has label
where
and
are the ranking functions of
and
, respectively, every other vertex of
has label less than
. So, attaching
to
does not increase the rank number of
. Since this argument is true for every
, it proves that
. □
Notes
Peer review under responsibility of Kalasalingam University.
References
- R.FlórezD.A.NarayanMaximizing the number of edges in optimal -rankingAKCE Int. J. Graphs Comb.121201518
- R.FlórezD.A.NarayanAn optimal -ranking characterization of oriented paths and cyclesBull. Inst. Combin. Appl.61201197108
- H.L.BodlaenderJ.S.DeogunK.JansenT.KloksD.KratschH.MüllerZ.TuzaRankings of graphsSiam J. Discrete Math.111998168181
- E.BruothM.HorňákOnline-ranking numbers for cycles and pathsDiscuss. Math. Graph Theory191999175197
- N.J.A. Sloane, The On-Line Encyclopedia of Integer Sequences, http://oeis.org/.
- N.DeoM.J.QuinnPascal graphs and their propertiesFibonacci Quart.2131983203214
- D.RomikShortest paths in the tower of Hanoi graph and finite automataSIAM J. Discrete Math.202006610622
- W.T.TutteGraph Theory2001Cambridge University PressNew York