A linear time algorithm to compute square of interval graphs and their colouring

Peer review under responsibility of Kalasalingam University.

Abstract

The square of a graph , denoted by , is a graph on the same vertex set such that two vertices and are adjacent in if and only if there is a path of length one or two between and in . In this article, a new linear time algorithm is presented to compute from when is an interval graph. Also a linear time algorithm is designed to find all the maximal cliques of from . Application of square of interval graphs in the field of -labelling problem is also discussed. Finally, it is shown that -labelling number of an interval graph can be computed in linear time.

Keywords:

• Interval graph
• Square of graph
• Clique
• -labelling

1 Introduction

The th power of a graph denoted by is a graph having the same vertex set as and the distance between two vertices in is one if and only if the distance between these two vertices in is at most . Obviously, . Due to their interesting properties and wide range of applications, power graph has been widely studied in the past. Power graph can be applied in different fields like routing in network, quantum random walk in physics, etc. The problem of colouring of power of graphs has also been considered in the past where the power of some specific classes of graphs like planar graph [1] and chordal graphs [2] has been studied. Vertex colouring of power of graphs has been used to solve different problems like interleaving [3], distributing data storage [4], sphere packing [5], etc. Square of graphs are also very useful in the study of radio communication networks. Vertex colouring of square of graphs are used to solve -labelling problem of graphs. Again -labelling problem has wide range of applications in the field of radio communication, mobile networking, frequency assignment [6], etc. -labelling problem is a particular case of -labelling problem for .

Table

Now,
i.e.
or,
this gives
finally	.

Table

Now,
i.e.
or,
this gives
finally	.

Table

Now,
i.e.
or,
this gives
finally	.

Table

		8.7

Table

		11.85.

Table

		34.6.

1.1 -labelling problem

The definition of -labelling is as follows.

Definition 1

-labelling of a graph is a function from to the set of non-negative integers such that if and if , where is the length of the shortest path (i.e. the number of edges) between the vertices and .

The span of -labelling is the difference between largest and smallest used labels. The minimum span over all possible labelling functions is denoted by .

For different values of and different problems have been addressed by the researchers. Roberts [7] investigated the problem for the case of , i.e. -labelling problem. Griggs and Yeh [8] studied the problem for the case of and . Bertossi and Bonuccelli [9] introduced a kind of integer control code assignment in packet radio networks to avoid hidden collisions. This problem is equivalent to the -labelling problem. Also, channel assignment in optical cluster-based networks can be modelled either as the - or -labelling problem. In general, channel assignment problems, with a channel defined as a frequency, a time slot, a control code, etc. can be modelled by an -labelling problem, for suitable values of and . In the literature, there are so many results related to -labelling problem [6] are available. In this paper, we focus our attention on -labelling of interval graphs.

1.2 Interval graph

An undirected graph is said to be an interval graph if the vertex set can be put into one-to-one correspondence with a set of intervals on the real line such that two vertices are adjacent in if and only if their corresponding intervals have non-empty intersection, i.e. there is a bijective mapping .

The set is called an interval representation of and is referred to as the interval graph of .

Interval graphs arise in the process of modelling many real life situations, specially involving time dependencies or other restrictions that are linear in nature. This graph and various subclass thereof arise in diverse areas such as archaeology, molecular biology, sociology, genetics, traffic planning, VLSI design, circuit routing, psychology, scheduling, transportation etc. Recently, interval graphs have found applications in protein sequencing, macro substitution, circuit routine, file organization, job scheduling, routing of two points nets and so on. In addition to these, interval graphs have been studied intensely from both the theoretical and algorithmic point of view. A brief discussion about interval representation of interval graphs and their properties are presented in Section 2.

1.3 Motivation of the work

Due to wide range of applications, -labelling problems has been widely studied over the lase two decades. In the algorithmic point of view the problem is NP-complete for general graphs. In case of interval graph, -labelling problem is polynomially solvable [10] and the complexity is still open for -labelling problem [11]. But, there is no such algorithm for -labelling of interval graph. Motivated from these we studied -labelling problem on interval graphs. To solve the problem we find the square of the given graph. Square of a graph play an important role in the field of graph theory. Note that the square of an interval graph is also an interval graph [12]. Thus designing a simple linear time algorithm to compute square of graphs is also the motivation of our work.

1.4 Our contribution

To the best of our knowledge there is no algorithm is available to compute the interval representation of from an interval representation of . In this paper, a linear time algorithm is designed to compute interval representation of . Also, a linear time algorithm is presented to compute all maximal cliques of . A good relationship is established between -labelling of a graph and colouring of square of graph. By using this relation we prove that -labelling of interval graphs can be computed in linear time.

2 Preliminaries

The graphs used in this work are connected, simple, i.e. without self loop or multiple edges. Let be a graph with vertex set and edge set . be denote the distance between and in a graph , which is the length of the shortest path joining and . denotes the set of one neighbours (or nbd) called the open neighbourhood of the vertex . The set denotes the closed neighbourhood of . Similarly, 2-nbd vertices of is denoted by and is defined as . represents the degree of the vertex . Number of edges and vertices of a graph is denoted by and respectively. A set is called a clique if for every pair of vertices of has an edge. The number of vertices of the clique represents its size. A clique of a graph is called maximal if there is no clique of which properly contains as a subset. Again, a clique with -vertices is called -clique. A clique is called maximum if there is no clique of of larger cardinality. The number of vertices of the maximum clique of is denoted by and is called the clique number of .

The definition of interval graph is given below.

Definition 2

Interval Graph

An undirected graph is an interval graph if the vertex set can be put into one-to-one correspondence with a set of intervals on the real line such that two vertices are adjacent in if and only if their corresponding intervals have non-empty intersection.

Here, we assume that the input graph is given by an interval representation which is the set of sorted intervals labelled by .

Let , where , ; be the interval representation of the given interval graph , , and are respectively the left and the right endpoints of the interval . Without any loss of generality, we assume that each interval contains both its endpoints and that no two intervals share a common endpoint. Also, we assume that the intervals in are indexed by increasing right endpoints, that is, . This indexing is known as IG ordering.

Let us define an array which contains the end points on intervals of an interval graph on real line in increasing order. That is, the array is the collection of all ’s and ’s for all . For example, for the graph of Fig. 1, , i.e. and so on. For each element of , three fields, , and are define as follows.

Fig. 1 An interval representation and the corresponding interval graph .

of the real line of the th endpoint ,

if is the endpoint of the interval ,

For the graph , we assume that the difference between any two consecutive is one unit on .

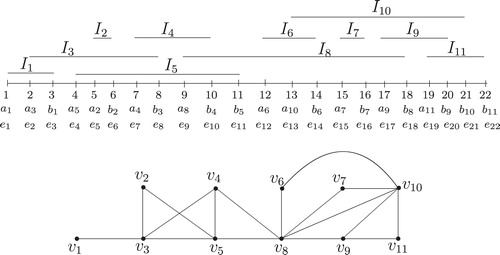
In Fig. 1, a set of intervals and their interval representation are given. In this figure, for ,

and .

For ,

and .

For ,

and .

For ,

and .

Interval graphs and many of its applications are discussed extensively in [13–^{[14][15][16][17][18][19]}20]. This graph satisfies lot of intersecting properties. We just point out some of them.

Lemma 1

[21]

The graph is an interval graph if and only if there exist an ordering of its vertices such that and then .

Lemma 2

[13]

The maximal clique of an interval graph can be linearly ordered such that for every vertex , the maximal clique containing occurs consecutively.

2.1 Notation

Here we present some notations which are necessary for the rest of the paper.

For each vertex , represents the highest number vertex of . That is, and , where is the number of vertices.

Let represent the set of vertices ,

i.e. .

The vertices are ordered according to the increasing values of right endpoints (’s) on real line. We can also say that the vertices are ordered according to the increasing value of where .

Let be the right endpoint of the interval corresponding to the vertex . Thus,

value of th endpoint on real line,

and

.

For each interval corresponding to the vertex , we define the followings:

: is the right endpoint of the interval corresponding to the vertex and

: is the nearest left endpoint from such that .

For some vertex (or interval ), may not be exist. In this case we consider .

For each and , let us define an array which contains the value of on real line. Thus,

value of endpoint on real line, and

.

Again, for each and , we define an array which contains the value of on real line. Thus,

value of endpoint on real line, and

.

If for some does not exist (i.e. ) then we call that the corresponding does not exist. In this case, we set a very large value (say ) for . Thus, if then (where tends to infinity on ).

For the graph of Fig. 1, for each , , and are shown in Table 1.

Table 1 The value of and .

		does not exist
		does not exist
		does not exist
		does not exist
		does not exist
		does not exist

Now, we define an array , where is the th endpoint of the graph . Like , also contain three fields, say , , and .

Lemma 3

If and then .

Proof

From the definition of , and the equality sign hold only when . Thus, and . Now, two cases arise.

Case 1. When .

From the definition of , it is clear that there is an edge between and . Thus, from Lemma 1, . Therefore the set must contain the vertex . So, . That is, . Therefore, in this case implies .

Case 2. When .

We have the result . So, . Therefore, in this case implies .

Thus, from both the cases, we conclude that implies .  □

3 Square of an interval graph

Definition of square of an interval graph is stated below.

Definition 3

Let , where be an interval graph. The square of denoted by of is a graph having the same vertex set as and having an edge connecting to if and only if to are at distance at most two in .

In [12], Raychaudhuri shown that interval graph classes are closed under power. Thus we conclude the following lemma.

Lemma 4

If is an interval graph then is also an interval graph.

Here we present a linear time algorithm to find of an interval graph .

3.1 Algorithm to compute

We assume that the distance between any two consecutive (for the input graph ) is one unit on . Our main aim is to compute the array from by adjusting the value of on real line. Since there are uncountable number of points between two consecutive ’s. Therefore, we can increase the value of (i.e. ) and set between two consecutive ’s with there proper position to compute the graph . We call the new value of as . Finally, we set for the th endpoints of the interval representation of .

Since is the right endpoint of the interval corresponding to , is the right endpoint of the interval corresponding to the vertex and is the nearest left endpoint of an interval (say , i.e. ) from such that . Thus, in , the interval (corresponding to the vertex ) not intersect the interval . Therefore, to compute we have to increased the value of on in such a way that the new value of is less than the value of on . Let is the new value of in the interval representation of and is the value of . Again, let and (where ) be the values of two consecutive endpoints of the interval representation of . Thus, unit. Now, we want to set in such a way that . So, we set . Therefore, if then the above condition hold. So, . Again, takes the value from 1 to . Thus, we set .

The algorithm is discussed below.

3.2 Analysis of the algorithm

Some results related to the algorithm is discussed below.

Lemma 5

maintain the same ordering of the vertices of .

Proof

Since the vertices of an interval graph are ordered by increasing right endpoints of the intervals. Thus, implies and vice-versa. Now we shown that algorithm IG2 maintain the same ordering of vertices of . That is, also hold for .

Since the array contain endpoints on the real line . Let and be two right endpoints of such that . Obviously, . That is, on . Now, from Lemma 3, if then . That is, implies and . Different cases arise.

Case 1. When for .

In this case, and we set as .

Case 2. When for .

In this case, and we set as .

Case 3. When and does not exist (i.e. ) for .

In this case, we set as .

Thus, from all the cases we conclude that if in then it also true for the graph . Hence the lemma. □

Proof of correctness of algorithm IG2 is given below.

Theorem 1

Algorithm IG2 correctly compute the graph from .

Proof

From the definition of , we have in if and only if and are at distance at most two in . Thus all the 2-nbd vertices of with index greater than must be adjacent to . Since is the right endpoint of the interval corresponding to , is the right endpoint of the interval corresponding to the vertex and is the nearest left endpoint of an interval (say , i.e. ) from such that . Thus, in , the interval (corresponding to the vertex ) not intersect the interval . Therefore, to compute we have to increased the value of on in such a way that the new value of is less than the value of on . Thus, in Step 2.2, we set , where is the value of on . Here we choose in such a way that lie between two consecutive ’s in . Now the distance between two consecutive ’s (for the graph ) is one unit on . Therefore, if we set (since ) then the above condition hold.

Now, let such that . That is, in , is adjacent to all the vertices with index greater than . Thus, we can say that there is no vertex () in such that in . Therefore, in this case we increase the right endpoint of , i.e. and set the new value of after (i.e. ). Thus, in Step 2.2, we set . Hence from the above discussion, we conclude that algorithm IG2 follow the definition of and in Lemma 5, we proved that algorithm IG2 follow the same vertex ordering of . Therefore, we conclude that algorithm IG2 correctly compute the graph from a given interval graph .  □

Theorem 2

Time complexity of the algorithm is .

Proof

In Step 1, for each , we have to check , and . Thus, for each , Step 1 take constant time. In Step 2, for each , we set , . So, this computation also takes constant time. In Step 2.1, we have to find the value of . To compute , first we have to compute , which is the value on . Now, can be computed by finding the vertex . So, can be computed in time. Now, to find , we have to scan the array from to right. Since the graph is connected, so there exist an interval (say ) which contains both the endpoints and . Therefore, to compute , it again take time. Now, is the value of on . So, to find , it take time. In Step 2.2, to set , it take constant time. Step 3. take time. Thus the overall time complexity is , i.e. as . Hence the result.  □

3.3 An example

We consider an interval graph () of 11 vertices (see Fig. 1) and compute the interval representation of (see Fig. 2) by Algorithm IG2. For the graph of Fig. 1, hold for .

Fig. 2 Interval representation of of the graph of Fig. 1 computed by Algorithm IG2.

In this case and .

Now, hold for .

In this case, and .

Now, we find for .

For ,

For ,

Similarly, .

Now, for

Similarly, and .

4 Algorithm to compute all maximal cliques of

In this section, we design a linear time algorithm to find all the maximal cliques of when an interval graph is given. There is an algorithm to compute all maximal cliques of an interval graph [22]. Thus, using the algorithm of [22], all maximal cliques can be computed in time for , as it is an interval graph, where is the sum of the size of all cliques. In the following algorithm we find all the maximal cliques of without computing the graph .

Lemma 6

For each vertex in , form a clique in .

Proof

From the definition of , it is the highest number adjacent vertex of . That is, is an adjacent vertex of with maximum right end point (’s). Thus all the 2-neighbourhood vertices of with index greater than must be adjacent to .

For some , let is of the form.

.

Since is a closed neighbourhood of , so it contains and both. Thus in , distance between any two vertices of is at most 2. Again, contains the same vertex set of having an edge connecting – if and only if and are at distance at most 2 in . So, obviously forms a clique in .  □

The algorithm is as follows.

In the next theorem a proof of correctness and the time complexity of Algorithm MCG2 is given.

Theorem 3

Algorithm MCG2 correctly computes all maximal cliques (’s) in time.

Proof

In Step 3.1 of Algorithm MCG2, we compute , where . Again, from Lemma 6, form a clique in . Now our aim is to show that the cliques are linearly ordered and the cliques are maximal.

The elements of the set are in increasing ordered and any two consecutive elements of are adjacent. Let and be two consecutive elements of . So, . Therefore, and . That is, . Therefore and there common intersection contain at least two elements. Therefore, the cliques are in linearly ordered. Now, in Step 3.2, mark the vertices of in the list and the process will continue until all the vertices of are marked. Within this computation, we now shown that all the cliques are maximal.

Suppose, for a vertex in , let . So, form a clique (by Lemma 6). If possible, let , where and also form a clique in . Thus the distance between and is at most 2 in . So, must be adjacent to as the right end point of is maximum among all the adjacent vertices if . But , which contradict our assumption that . Therefore, in . Hence does not form a clique and is a maximal clique.

In Step 1, computation of takes i.e. time. In Step 2, to compute the set , takes time. is the closed nbd of , where . Thus Step 3.1 take i.e. time. Similarly, Step 3.2 also take time. Therefore, the overall time complexity of Algorithm MCG2 is .  □

4.1 An example

We consider an interval graph of 11 vertices (see Fig. 1) and compute all maximal cliques of by Algorithm MCG2.

By Step 1, and .

Now, in Step 2, the set .

By Step 3.1, .

By Step 3.2, marked vertices of are and .

Again, .

Therefore the marked vertices are and .

Now, .

So, the marked vertices are and .

Again, .

Here, the marked vertices are and . So, all the vertices of are marked. Therefore, in this step the procedure is stopped. Hence the maximal cliques of are and .

5 -labelling of interval graphs

Graph colouring problem is one of the key topics in the field of graph theory. Graph colouring are motivated by problems like channel assignment in wireless communications, traffic phasing, task assignment, fleet maintenance, etc. In vertex colouring of graph there is only one restriction on the adjacent vertices. -labelling problem is the generalization of vertex colouring problem where the adjacent vertices and the vertices at distance two are to be labelled. This labelling is also known as distance two labelling. Specially , and -labelling of graphs have been studied for their wide range of applications. Paul et al. [10] have shown that -labelling problem is polynomially solvable for interval graphs. We [11] also investigated -labelling problem on interval graphs and find a good upper bound for these classes of graphs. In this article, we have shown that -labelling problem on interval graph can be solved in linear time. The definition of -labelling is as follows.

Definition 4

-labelling of a graph is a function from to the set of non-negative integers such that if and if , where is the length of the shortest path (i.e. the number of edges) between the vertices and .

The span of -labelling is the difference between largest and smallest used labels. The minimum span over all possible labelling functions is denoted by .

Some important results are discussed below.

Theorem 4

-labelling problem of an interval graph is equivalent to the vertex colouring problem of .

Proof

In -labelling, the label difference of two vertices is at least 1 if the vertices are adjacent and the label difference of two vertices is also at least one if the vertices are at distance two. Now in , if and only if and are at distance at most two in . Thus, for the graph there is no restriction for distance two vertices as in converted to in . Therefore, -labelling problem of converted to -labelling problem of . In -labelling problem there is no restriction for distance two vertices and if two vertices are adjacent then there label difference is at least one. Thus -labelling problem is nothing but a simple vertex colouring problem. Hence the result.  □

Since interval graphs are perfect [13]. Thus, the number colours needed to colour an interval graph is , where is the clique number of . Again, -labelling problem is equivalent to graph colouring problem. Thus, , where is the chromatic number of . Pal et al. [21] have designed a linear time algorithm to colour an interval graph. To do this, they use the interval representation of interval graph. Hence we conclude the following lemma.

Lemma 7

[21]

An interval graph can be labelled by -labelling (or colouring) in time and .

We recall that if is an interval graph then is also an interval graph as interval graph classes are closed under power [12]. Therefore, we conclude the following result.

Theorem 5

An interval graph can be labelled by -labelling in time and .

Proof

From Theorem 4, -labelling problem is equivalent to -labelling problem of . Again, to compute the graph , -time is required (from Theorem 2). Now, to label the graph , -time is required (from Lemma 7) as is an interval graph. It is well known that . Therefore, . Thus, the overall time complexity to label an interval graph by -labelling is , i.e. . Hence the theorem.  □

6 Conclusion

-labelling problem has been widely studied over last two decades. The problem is NP-complete for general graph. There are only few classes of graphs for which they have efficient algorithms. In this paper, we have shown that the problem is polynomially solvable for interval graph. Also a linear time algorithm is designed to compute the square of an interval graph. It would be interesting to design a linear time algorithm to compute the square of permutation and trapezoid graphs as they are the super classes of interval graphs.

Notes

Peer review under responsibility of Kalasalingam University.