The forcing vertex detour monophonic number of a graph

Peer review under responsibility of Kalasalingam University.

Research supported by DST Project No. SR/S4/MS: 570/09.

Abstract

For any two vertices and in a connected graph , an – path is a monophonic path if it contains no chord, and a longest – monophonic path is called an – detour monophonic path. For any vertex in , a set is an -detour monophonic set of if each vertex lies on an – detour monophonic path for some element in . The minimum cardinality of an -detour monophonic set of is the -detour monophonic number of , denoted by . A subset of a minimum -detour monophonic set of is an -forcing subset for if is the unique minimum -detour monophonic set containing . An -forcing subset for of minimum cardinality is a minimum -forcing subset of . The forcing -detour monophonic number of , denoted by , is the cardinality of a minimum -forcing subset for . The forcing -detour number of is , where the minimum is taken over all minimum -detour monophonic sets in . We determine bounds for it and find the same for some special classes of graphs. Also we show that for every pair of integers with , there exists a connected graph such that and for some vertex in .

Keywords:

• Detour monophonic path
• Vertex detour monophonic number
• Forcing vertex detour monophonic number

1 Introduction

By a graph we mean a non-trivial finite undirected connected graph without loops or multiple edges. The order and size of are denoted by and respectively. For basic graph theoretic terminology we refer to Harary [1]. For vertices and in a connected graph , the distance is the length of a shortest path in . An path of length is called an geodesic. The neighborhood of a vertex is the set consisting of all vertices which are adjacent with . The closed neighborhood of a vertex is the set . A vertex is an extreme vertex of if the subgraph induced by its neighbors is complete.

The closed interval consists of all vertices lying on some geodesic of , while for , . A set of vertices is a geodetic set if , and the minimum cardinality of a geodetic set is the geodetic number . A geodetic set of cardinality is called a -set of . The geodetic number of a graph was introduced in [2] and further studied in [3–^[4]5].

The concept of vertex geodomination in graphs was introduced in [6] and further studied in [7]. Let be a vertex of a connected graph . A set of vertices of is an -geodominating set of if each vertex of lies on an geodesic in for some element in . The minimum cardinality of an -geodominating set of is defined as the -geodomination number of and is denoted by .

A chord of a path is an edge joining any two non-adjacent vertices of . A path is called a monophonic path if it is a chordless path. A longest monophonic path is called an detour monophonic path. The monophonic distance from to is defined as the length of a longest monophonic path (or detour monophonic path) in . The monophonic eccentricity of a vertex in is . The monophonic radius, of is and the monophonic diameter, of is . The monophonic distance was introduced in [8] and further studied in [9].

The concept of vertex detour monophonic number was introduced in [10]. Let be a vertex of a connected graph . A set of vertices of is an -detour monophonic set of if each vertex of lies on an detour monophonic path in for some element in . The minimum cardinality of an -detour monophonic set of is defined as the -detour monophonic number of and is denoted by . An -detour monophonic set of cardinality is called a -set of .

2 Forcing vertex detour monophonic number

Let be any vertex of a connected graph . Although contains a minimum -detour monophonic set there are connected graphs which may contain more than one minimum -detour monophonic set. For example the graph given in Fig. 2.1 contains more than one minimum -detour monophonic set. For each minimum -detour monophonic set in a connected graph there is always some subset of that uniquely determines as the minimum -detour monophonic set containing . Such sets are called “vertex forcing subsets” and we discuss these sets in this section. Also, forcing concepts have been studied for such diverse parameters in graphs as the graph reconstruction number [11], the domination number [12], and the geodetic number [13].

Fig. 2.1 The graph in Example 2.2.

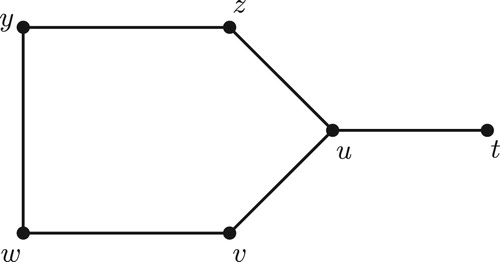
Definition 2.1

Let be a vertex of a connected graph and let be a minimum -detour monophonic set of . A subset of is called an -forcing subset for if is the unique minimum -detour monophonic set containing . An -forcing subset for of minimum cardinality is a minimum -forcing subset of . The forcing -detour monophonic number of , denoted by , is the cardinality of a minimum -forcing subset of . The forcing -detour monophonic number of is , where the minimum is taken over all minimum -detour monophonic sets in .

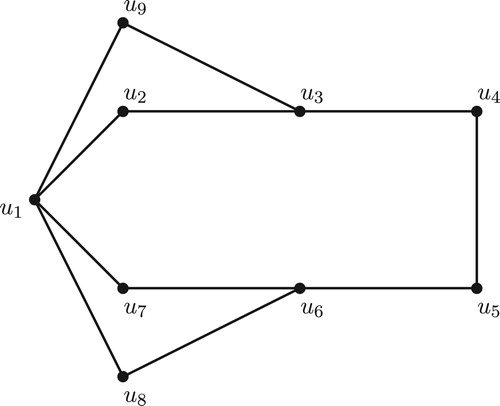
Example 2.2

For the graph given in Fig. 2.1, the minimum vertex detour monophonic sets, the vertex detour monophonic numbers, the minimum forcing vertex detour monophonic sets and the forcing vertex detour monophonic numbers are given in Table 2.1.

Table 2.1 The forcing vertex detour monophonic numbers of the graph given in Fig. 2.1.

Vertex	Minimum		Minimum forcing
	-detour		-detour
	monophonic sets		monophonic sets
		2		1
		3		1
		2		0
		2	,	1
		2		1
		2		0

The next theorem immediately follows from the definition of -detour monophonic number and forcing -detour monophonic number of a graph .

Theorem 2.3

For any vertex in a connected graph , .

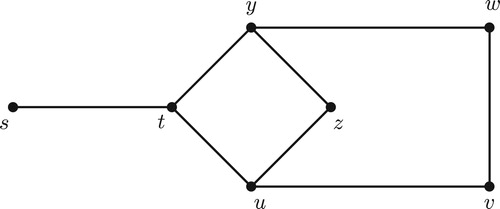
The bounds in Theorem 2.3 are sharp. For the graph given in Fig. 2.1, . Also, for the graph given in Fig. 2.2, and are the minimum -detour monophonic sets of and so . It is easily verified that no minimum -detour monophonic set is the unique minimum -detour monophonic set containing any of its proper subsets. It follows that and hence . The inequalities in Theorem 2.3 can be strict. For the graph given in Fig. 2.1, and . Thus .

Fig. 2.2 A graph with .

In the following theorem we characterize graphs for which the bounds in Theorem 2.3 are attained and also graphs for which .

Theorem 2.4

Let be a vertex of a connected graph . Then

(i) if and only if has a unique minimum -detour monophonic set.

(ii) if and only if has at least two minimum -detour monophonic sets and one of which is a unique minimum -detour monophonic set containing one of its elements.

(iii) if and only if no minimum -detour monophonic set of is the unique minimum -detour monophonic set containing any of its proper subsets.

Definition 2.5

A vertex of a connected graph is said to be an -detour monophonic vertex of if belongs to every minimum -detour monophonic set of .

For the graph in Fig. 2.3, and are the minimum -detour monophonic sets and so and are the -detour monophonic vertices of . In particular, every extreme vertex of other than is an -detour monophonic vertex of .

Fig. 2.3 A graph with vertex detour monophonic vertices.

The following theorem and corollary follows immediately from the definitions of an -detour monophonic vertex and forcing -detour monophonic subset of .

Theorem 2.6

Let be a vertex of a connected graph and let be the set of relative complements of the minimum -forcing subsets in their respective minimum -detour monophonic sets in . Then is the set of -detour monophonic vertices of .

Corollary 2.7

Let be a connected graph and a minimum -detour monophonic set of . Then no -detour monophonic vertex of belongs to any minimum -forcing subset of .

Theorem 2.8

Let be a vertex of a connected graph and let be the set of all -detour monophonic vertices of . Then .

Proof

Let be any minimum -detour monophonic set of . Then , and is the unique minimum -detour monophonic set containing and so .  □

Corollary 2.9

If is a complete graph or a tree or a complete bipartite graph, then for any vertex in .

Proof

It is easily seen that has unique minimum -detour monophonic set for any vertex in . Hence the result follows from Theorem 2.4(i).  □

Theorem 2.10

For any vertex in the cycle of order , or according as is even or odd.

Proof

Let be a cycle of order . Let be any vertex in , say . If is even, then is the unique minimum -detour monophonic set of and so by Theorem 2.4(i), . If is odd, then and are the minimum -detour monophonic sets of . Hence it follows from Theorem 2.4(i) that . Clearly, is a minimum -forcing subset of and so .  □

Theorem 2.11

Let be the wheel.

(i) If is odd, then for any vertex in .

(ii) If is even, then or according as is or is in .

Proof

Let be a cycle of order and the vertex of . If is odd, then has the unique minimum -detour monophonic set of for any vertex in and so by Theorem 2.4(i), . Now, assume that is even. If , then is the unique minimum -detour monophonic set of and so by Theorem 2.4(i), . If , say , then and are the minimum -detour monophonic sets of . Hence it follows from Theorem 2.4(i) that . Clearly, is a minimum -forcing subset of and so .  □

We proved in Theorem 2.3 that for any vertex in . Already we have seen that if is a complete graph , then and for any vertex in . Also for the graph given in Fig. 2.4, and for the vertex . The following theorem gives a realization for these parameters when .

Fig. 2.4 A graph with and .

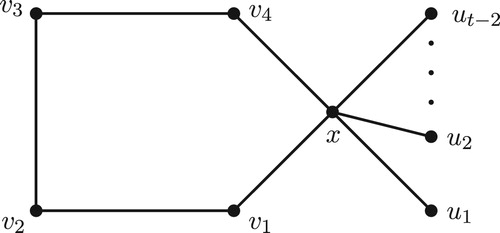
Theorem 2.12

For every pair of integers with , there exists a connected graph such that and for some vertex in .

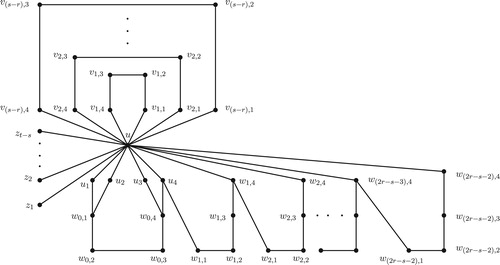
Proof

For each integer with , let be a path of order 4 and let be a star with . Let be the graph obtained from and by (i) join with and in (ii) join with and in (iii) join each with in (iv) join each with and (v) join with in . Now, let be the graph obtained from by adding new vertices and joining each with . The graph is shown in Fig. 2.5.

Let and let be the set of all extreme vertices of . Let , and . First we claim that . Now, we observe that a set of vertices of is a -set if and only if contains exactly one vertex from each set and contains so that . Since is an -detour monophonic set of with , it follows that .

Next, we prove that . Let be a -set of and let be any minimum -forcing subset of . Then, by Theorem 2.8, we get .

If , then there exists a vertex such that . It is clear that for some , say . Let . Then and is also a minimum -detour monophonic set of such that it contains , which is a contradiction to an -forcing subset of . Thus and so . □

Fig. 2.5 A graph with and .

3 Upper forcing vertex detour monophonic number

The cardinality of vertex forcing subsets depend on the corresponding minimum vertex detour monophonic set of . In this observation, we discuss these sets with minimum cardinality in the previous section. Now, we deal about vertex forcing subsets with maximum cardinality in this section.

Definition 3.1

Let be any vertex of a connected graph . The upper forcing -detour monophonic number, , of is the maximum forcing -detour monophonic number among all minimum -detour monophonic sets of .

Example 3.2

For the graph given in Fig. 2.1, the minimum vertex detour monophonic sets, the vertex detour monophonic numbers, the forcing vertex detour monophonic sets, the minimum forcing vertex detour monophonic numbers and upper forcing vertex detour monophonic numbers are given in Table 3.1.

Table 3.1 The upper forcing vertex detour monophonic numbers of the graph given in Fig. 2.1.

Vertex	-sets		-forcing subsets
		2		1	2
		3		1	2
		2		0	0
		2	,	1	1
		2		1	1
		2		0	0

From Table 3.1, the forcing vertex detour monophonic number and the upper forcing vertex detour monophonic number of a graph are different.

Next we present two theorems whose routine proof is omitted.

Theorem 3.3

For any vertex in a connected graph , .

Theorem 3.4

Let be a vertex of a connected graph . Then

(i) if and only if has a unique minimum -detour monophonic set.

(ii) if and only if has at least two minimum -detour monophonic sets and every -set is the unique -set containing one of its elements.

(iii) if and only if no minimum -detour monophonic set of is the unique minimum -detour monophonic set containing any of its proper subsets.

Theorem 3.5

For any vertex in the cycle of order , or according as is even or odd.

Proof

Let be a cycle of order . Let be any vertex in , say . If is even, then is the unique minimum -detour monophonic set of and so by Theorem 3.4(i), . If is odd, then and are the minimum -detour monophonic sets of . Hence it follows from Theorem 3.4(i) that . Also, is one of the minimum -detour monophonic set of . It is easily verified that any proper subset of is contained in some other minimum -detour monophonic set of and so .  □

Theorem 3.6

Let be the wheel.

(i) If is odd, then for any vertex in .

(ii) If is even, then or according as is or is in .

Proof

Let be a cycle of order and let be the vertex of . If is odd, then has the unique -set for any vertex in and so by Theorem 3.4(i), . Now, assume that is even. If , then -set is unique and so . If , say , then and are the minimum -detour monophonic sets of . Hence it follows that is the unique forcing -detour monophonic set of the minimum -detour monophonic set so that . Since is the -detour monophonic vertex of , by Corollary 2.7, we have .  □

Note that we have for every connected graph . The following theorem gives a realization result for the parameters and .

Theorem 3.7

For any three positive integers and with and , there exists a connected graph with and for some vertex in .

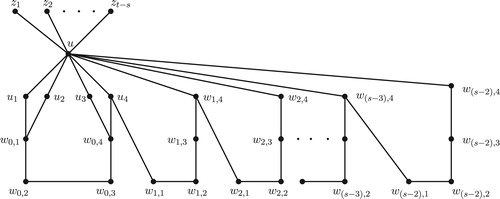
Proof

We prove this theorem by considering 3 cases.

Case 1. . For each integer with , let be a path of order 4, for each integer with , let be another path of order 4 and let be a star with . Let be the graph obtained from and by (i) join with and in (ii) join with and in (iii) join each with in (iv) join each with (v) join with in and (vi) join each with in . Now, let be the graph obtained from by adding new vertices and joining each with . The graph is shown in Fig. 3.1.

Let and let be the set of all extreme vertices of . Let and . Also, for , let and . Now, we observe that a set of vertices of is a -set if contains exactly one vertex from each set , contains and contains for each exactly one set from . Hence . Since is an -detour monophonic set of with , it follows that .

Next, we prove that and . Let be any minimum -forcing subset of . Then by Theorem 2.8, . Since any subset of a minimum -detour monophonic set with cardinality less than contained in more than one minimum -detour monophonic set of , we have . It is easily seen that is a minimum -forcing subset of a minimum -detour monophonic set and is a minimum -forcing subset of a minimum -detour monophonic set of . It follows that and .

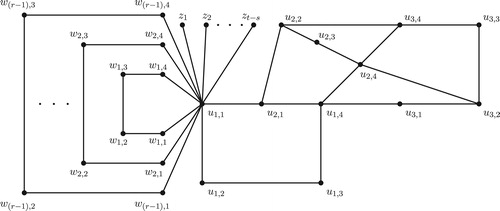
Case 2. . For each integer with , let be a path of order 4. Let be the graph obtained from by (i) join with and (ii) join with and (iii) join with and (iv) join with . For each integer with , let be a path of order 4. Let be the graph obtained from and by joining each and with in . The graph is obtained from by adding new vertices and joining each with in . The graph is shown in Fig. 3.2.

Let and let be the set of all extreme vertices of . Also, for , let and . Now, we observe that a set of vertices of is a -set if contains exactly one vertex from and contains , and for each exactly one set from . Hence . Since is an -detour monophonic set of with , it follows that .

Next, we prove that and . Let be any minimum -forcing subset of . Then by Theorem 2.8, . Since any subset of a minimum -detour monophonic set with cardinality less than contained in more than one minimum -detour monophonic set of , we have . It is easily seen that is a minimum -forcing subset of a minimum -detour monophonic set and is a minimum -forcing subset of a minimum -detour monophonic set of . It follows that and .

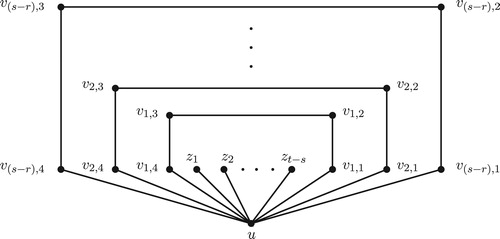
Case 3. . For each with , let be a path of order 4 and let be a star with . Let be the graph obtained from and by (i) join with in and (ii) join with in . The graph is shown in Fig. 3.3.

Let and let be the set of all extreme vertices of . For , let and . Now, we observe that a set of vertices of is a -set if contains and contains for each exactly one set from . Hence . Since is an -detour monophonic set of with , it follows that .

Next, we prove that and . Let be any minimum -forcing subset of . Then by Theorem 2.8, . Since any subset of a minimum -detour monophonic set with cardinality less than contained in more than one minimum -detour monophonic set of , we have . It is easily seen that is a minimum -forcing subset of minimum -detour monophonic set and is a minimum -forcing subset of a minimum -detour monophonic set of . It follows that and .  □

Fig. 3.1 The graph in Case 1 of Theorem 3.7 with and .

Fig. 3.2 The graph in Case 2 of Theorem 3.7 with and .

Fig. 3.3 The graph in Case 3 of Theorem 3.7 with and .

Problem 3.8

For any three positive integers and with and , does there exist a connected graph with and for some vertex in ?

Notes

Research supported by DST Project No. SR/S4/MS: 570/09.

Peer review under responsibility of Kalasalingam University.