Alpha labelings of full hexagonal caterpillars

Peer review under responsibility of Kalasalingam University.

Abstract

Barrientos and Minion (2015) introduced the notion of generalized snake polyomino graphs and proved that when the cells are either squares or hexagons, then they admit an alpha labeling. Froncek et al. (2014) generalized the notion by introducing straight simple polyominal caterpillars with square cells and proved that they also admit an alpha labeling.

We introduce a similar family of graphs called full hexagonal caterpillars and prove that they also admit an alpha labeling. This implies that every full hexagonal caterpillar with edges decomposes the complete graph for any positive integer .

Keywords:

• Alpha labeling
• Graceful labeling
• Graph decomposition

1 Introduction

At the Forty-Fifth Southeastern International Conference on Combinatorics, Graph Theory, and Computing in Boca Raton in March 2014, Minion presented her joint results with Barrientos on alpha labelings of snake polyominoes and other related graphs (they later published it in [1]). Froncek, Kingston, and Vezina [2] generalized the notion by introducing straight simple polyominal caterpillars with square cells and proved that they also admit an alpha labeling. In this paper, we introduce a similar class of graphs with hexagonal cells, called full hexagonal caterpillars and prove that they also admit an alpha labeling.

Barrientos and Minion [1] define a snake polyomino as a chain of edge-amalgamated cycles of the same length with the property that shares one edge with , shares one edge with , and for , each shares one edge with and another edge with . Note that no edge appears in more than two of those cycles. They proved that such a snake polyomino has an alpha labeling whenever the cycles are of length four or six.

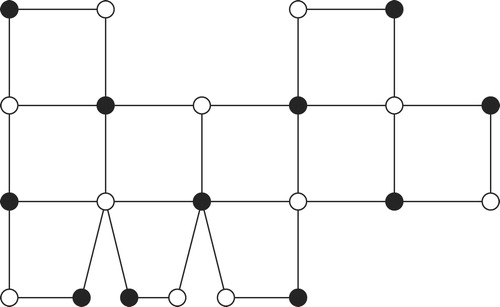
Froncek, Kingston, and Vezina [2] generalized this notion for square polyominoes and defined a straight simple polyominal caterpillar as follows. The spine of the caterpillar is a straight snake polyomino in which the edges of shared with and are non-adjacent, which means that every vertex is of degree at most three. The spine can be also viewed as the Cartesian product . We denote the vertices of the two paths as and , respectively. A straight simple polyominal caterpillar then can be constructed by amalgamating at most one four-cycle to each of the edges and for . Notice that we can amalgamate the four-cycles to none, one, or both of the two edges and for any admissible value of . The number of four-cycles in the spine is the length of the caterpillar. An example is shown in Fig. 1.

Fig. 1 Straight simple polyominal caterpillar.

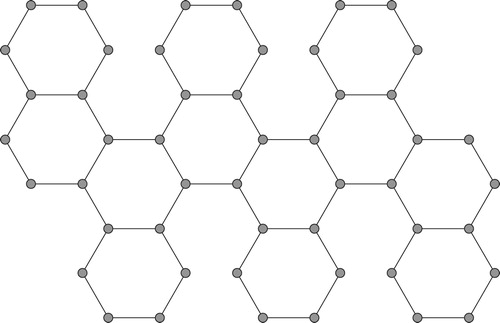
We generalize the notion for hexagonal polyominoes in a rather restricted form and define full hexagonal caterpillars of length as follows. The spine is a hexagonal chain (see [1]) consisting of six-cycles, , where consists of edges numbered consecutively clockwise. Cycle shares edge with , shares edge with and with , shares edge with and with , and so on. More precisely, we have when is even and when is odd.

The legs are six-cycles , where consists of edges numbered consecutively clockwise. For , cycle shares edge with , where when is odd, and when is even. An example of a full hexagonal caterpillar of length is shown in Fig. 2.

Fig. 2 Full hexagonal caterpillar .

2 Supporting results and tools

Rosa [3] introduced in 1967 certain types of vertex labelings as important tools for decompositions of complete graphs into graphs with edges.

A labeling of a graph with edges is an injection from , the vertex set of , into a subset of the set of elements of the additive group . Let be the injection. The length of an edge is defined as . The subtraction is performed in and hence . If the set of all lengths of the edges is equal to and , then is a rosy labeling (called originally -valuation by Rosa); if instead, then is a graceful labeling (called -valuation by Rosa). A graph admitting a graceful labeling is called a graceful graph. A graceful labeling is said to be an alpha labeling if there exists a number (called the boundary value) with the property that for every edge with it holds that . Obviously, must be bipartite to allow an alpha labeling. A graph admitting an alpha labeling is called an -graph. For an exhaustive survey of graph labelings, see [4] by Gallian.

Let be a graph with at most vertices. We say that the complete graph has a -decomposition if there are subgraphs of , all isomorphic to , such that each edge of belongs to exactly one . Such a decomposition is called cyclic if there exists a graph isomorphism such that for and .

Each graceful labeling is of course also a rosy labeling. The following theorem was proved by Rosa in [3].

Theorem 2.1

A cyclic -decomposition of for a graph with edges exists if and only if has a rosy labeling.

The main idea of the proof is the following. has exactly edges of length for every and each copy of contains exactly one edge of each length. The cyclic decomposition is constructed by taking a labeled copy of , say , and then adding an element to the label of each vertex of to obtain a copy for .

For graphs with an alpha labeling, even stronger result was proved by Rosa.

Theorem 2.2

If a graph with edges has an alpha labeling, then there exists a -decomposition of for any positive integer .

The proof is based on the observation that if we increase all labels in the partite set with labels exceeding by , then all edge lengths will also stretch by . Hence, we can take copies of and increase the labels in the upper partite set in the th copy by , where . This way we obtain edge lengths , each exactly once.

Barrientos and Minion [1] made the following observation.

Theorem 2.3

If of order with edges and of order with edges are two -graphs with boundary values and , respectively, then there exists their edge-amalgamation of order with edges that is also an -graph with boundary value .

For let be the partite sets with the lower labels, that is, at most , and the sets with the upper labels. Call the respective labelings and . Further, let be the longest edge of of length and the shortest edge of of length 1. Then indeed , and .

Barrientos and Minion observed that one can amalgamate with and with and increase the labels in and by and labels in by to obtain the desired graph . The amalgamated edge arising from and is called the link. Notice that the shortest edge of is in the subgraph arising from while the longest one is in the subgraph arising from . The edge-amalgamation of and as described above will be denoted as .

It is easy to observe that this concept can be used for consecutive amalgamation of any number of -graphs into a larger -graph. We will use that observation in the next section.

3 Construction

Using the above result, we now prove that every full hexagonal caterpillar is an -graph. The proof will be performed by strong induction. We first prove the result for full hexagonal caterpillars of even length. We start with the base case for .

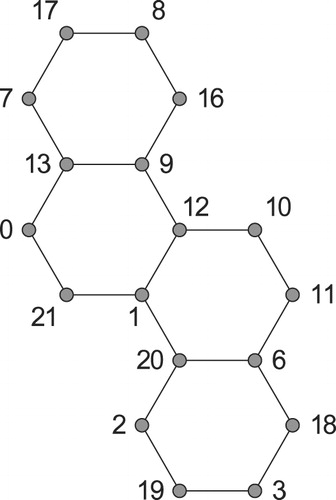
The assertion of the lemma below follows directly from the labelings in Fig. 3.

Fig. 3 Full hexagonal caterpillar .

Lemma 3.1

The full hexagonal caterpillar of length 2 has an alpha labeling such that the edge has length 21 and the edge has length 1.

Now we are ready to prove our result for even.

Theorem 3.2

The full hexagonal caterpillar of an even length has an alpha labeling such that the edge has length and the edge has length 1.

Proof

The base case has been established in Lemma 3.1. Now suppose we have a full hexagonal caterpillar of an even length . Obviously, it has edges. We remove the cycles except edge , which is equal to and belongs to as well. We obtain a full hexagonal caterpillar of even length . By our induction hypothesis, has an alpha labeling with of length and of length 1.

Now we apply Theorem 2.3, setting and . It should be clear that is the amalgamation of the two full hexagonal caterpillars and with the required alpha labeling.  □

An analogous result for odd is slightly weaker, as we do not require the shortest edge to be in any specific position.

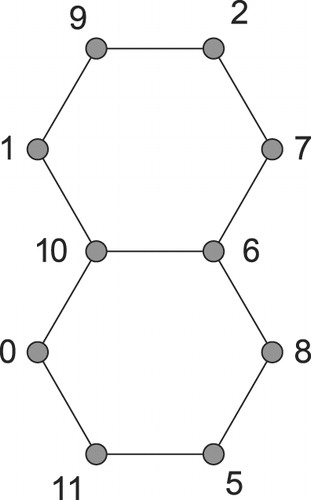
Lemma 3.3

The full hexagonal caterpillar of length 1 has an alpha labeling such that the edge has length 11.

The labeling is shown in Fig. 4.

Fig. 4 Full hexagonal caterpillar .

Theorem 3.4

The full hexagonal caterpillar of an odd length has an alpha labeling such that the edge has length .

Proof

The base case follows from Lemma 3.3. We start with a full hexagonal caterpillar of an odd length . Obviously, it has edges. We remove the cycles and except edge , which is equal to and belongs to as well. Now we have a full hexagonal caterpillar of even length . By Theorem 3.2, has an alpha labeling with of length and of length 1.

We again apply Theorem 2.3 with and . It should be clear that the amalgamation of the two full hexagonal caterpillars and is with the required alpha labeling.  □

Combining Theorems 3.2 and 3.4, we get our main result immediately.

Theorem 3.5

Every full hexagonal caterpillar admits an alpha labeling.

The result on decompositions of complete graphs into full hexagonal polyominal caterpillars follows directly from Theorems 3.5 and 2.2.

Corollary 3.6

Every full hexagonal polyominal caterpillar with edges decomposes the complete graph for any positive integer .

4 Conclusion

There are two obvious directions for further research. One is looking at hexagonal caterpillars that are not full. That in our notation means that only some of the leg hexagons would be present. Although it does not seem so hard at the first glance, one has to realize that because a hexagon itself does not admit an alpha labeling, and also an alpha labeling of with the proper placement of the edge of length one is not known (and although we are not going to present a proof here, we are reasonably sure that it does not exist), we would have to consider eight starting cases for caterpillars of length three. Studying only hexagonal caterpillars of even length is not much easier either, since we were not able to find a proper alpha labeling for a spine segment of length two with no legs attached (again, we are reasonably sure that it does not exist).

Another possibility would be to look at the case where more than one leg hexagon would be attached to the same spine edge. This seems to be even more complex problem than the above one. Finally, while Barrientos and Minion proved that all hexagonal snakes (they called them chains) admit alpha labelings, one could ask under what conditions there would exist alpha labelings of hexagonal rings.

Notes

Peer review under responsibility of Kalasalingam University.