Rainbow connection number of amalgamation of some graphs

Peer review under responsibility of Kalasalingam University.

Abstract

Let be a nontrivial connected graph. For , we define a coloring of the edges of such that adjacent edges can be colored the same. A path in is a rainbow path if no two edges of are colored the same. A rainbow path connecting two vertices and in is called rainbow – path. A graph is said rainbow-connected if for every two vertices and of , there exists a rainbow – path. In this case, the coloring is called a rainbow -coloring of . The minimum such that has a rainbow -coloring is called the rainbow connection number of .

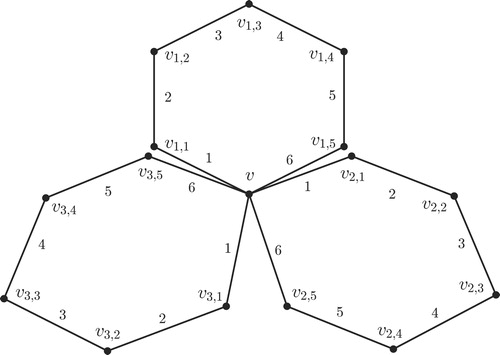
For and , let be a finite collection of graphs and each has a fixed vertex called a terminal. The amalgamation is a graph formed by taking all the ’s and identifying their terminals.

We give lower and upper bounds for the rainbow connection number of for any connected graph . Additionally, we determine the rainbow connection number of amalgamation of either complete graphs, or wheels, or fans.

Keywords:

• Amalgamation
• Complete graph
• Fan
• Rainbow connection number
• Wheel

1 Introduction

All graphs in this paper are simple, finite, and undirected. The concept of rainbow coloring was introduced by Chartrand et al. [1]. Let be a nontrivial connected graph. For , we define a coloring of the edges of such that adjacent edges can be colored the same. A path in is a rainbow path if no two edges of are colored the same. A rainbow path connecting two vertices and in is called rainbow path. A graph is said rainbow-connected if for every two vertices and of , there exists a rainbow path. In this case, the coloring is called a rainbow k-coloring of . The minimum such that has a rainbow -coloring is called the rainbow connection number of . Clearly where denotes the diameter of .

Fig. 1 A rainbow 6-coloring of where and .

Fig. 2 A rainbow 14-coloring of amalgamation of tree.

Fig. 3 A rainbow 3-coloring of where and .

Fig. 4 A rainbow 3-coloring of where and .

Fig. 5 A rainbow 3-coloring of where and .

Chartrand et al. [1] determined the rainbow connection number for some classes of graphs. They showed that if and only if is a complete graph, and if and only if is a tree. They also determined the rainbow connection number of cycles and wheels. In [2], Syafrizal Sy et al. determined the rainbow connection number of fans. The rainbow connection numbers of some other graph classes, namely flower graphs, origami graphs, pizza graphs, crossed prism graphs, pencil graphs, rocket graphs, and stellar graphs can be seen in [3–^[4][5][6]7], and [8]. Chakraborty et al. [9] showed that computing the rainbow connection number of a graph is NP-Hard.

There are some results about rainbow connection number of graphs resulted from graph operations. Li and Sun [10] obtained some results on bounds for rainbow connection number of product of graphs, including Cartesian product, composition (lexicographic product), and join of graphs. Basavaraju et al. [11] determined bounds for rainbow connection number of graphs that are obtained by Cartesian product, lexicographic product, strong product, and the operation of taking the power of graph according to the radius of graphs. Gologranc et al. [12] investigated bounds for rainbow connection number on direct, strong, and lexicographic product of graphs. An overview about rainbow connection number can be found in a survey by Li et al. [13] and a book of Li and Sun [14].

2 Main results

The following definition of an amalgamation of graph is taken from [15]. For and , let be a simple connected graph and for some . For , let be a finite collection of graphs and each , has a fixed vertex called a terminal. The amalgamation is a graph formed by taking all the ’s and identifying their terminals.

Let . We denote the identified vertex as and define .

The following theorem provides a sharp lower and upper bound for the rainbow connection number of amalgamation of arbitrary graphs.

Theorem 2.1

For , let be a finite collection of graphs and each has a fixed vertex called a terminal. If is the amalgamation of , , then

Proof

We obtain the lower bound by the fact that . Let be a rainbow -coloring of . We define a coloring as follows. We consider any two vertices .

Case 1.	=	for . There exists a rainbow path by coloring corresponding to coloring .
Case 2.	=	and for some and in with . There exists a rainbow path and a rainbow path by coloring corresponding to coloring and , respectively, where is the identified vertex in corresponding to the terminal in each . We can find a rainbow path by identifying vertex in a rainbow path and a rainbow path since we use different colors in and by coloring .

So, is a rainbow coloring. Thus, . □

In the next two theorems, we prove the existence of an amalgamation graph whose rainbow connection number satisfies either the lower or upper bound in Theorem 2.1.

Theorem 2.2

Let and be two positive integers with and . Let where for each , is a cycle . For even and , or odd and , .

Proof

By Theorem 2.1, we only need to show that . We define

Let be the subgraph of induced by . We consider two cases.

Case 1.

=

is even and We can check that . We define a coloring as follows. where and . We consider any two vertices . If or , and for some , and for some and in , then there exists a rainbow path between and since every edge in has different color. Let and for some and with , and for some and in . Subcase 1. = There exists a rainbow path from to , namely . Subcase 2. = There exists a rainbow path from to , namely . So, is a rainbow coloring. Thus, for even and .

Case 2.

=

is odd and We can check that . We define a coloring as follows. If or , and for some , and for some and in , then there exists a rainbow path from to since and there are different colors used in by coloring above. Let and for some and in with , and for some and in . Subcase 1. = for in and for in There exists two rainbow paths from to , namely and . Subcase 2. = for in and for in There exists two rainbow paths from to , namely and . For another two vertices, we can find a unique rainbow path between and by identifying vertex in a rainbow path whose length is equal to and a rainbow path whose length is equal to where is the identified vertex. So, is a rainbow coloring. Thus, for odd and .

Hence, and so for even and , or odd and . □

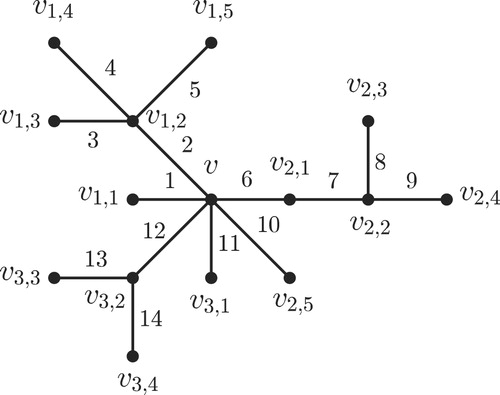
Theorem 2.3

Let be a positive integer with and where for each , is an arbitrary tree . Then .

Proof

We obtain that is also a tree and . By [9], we get . □

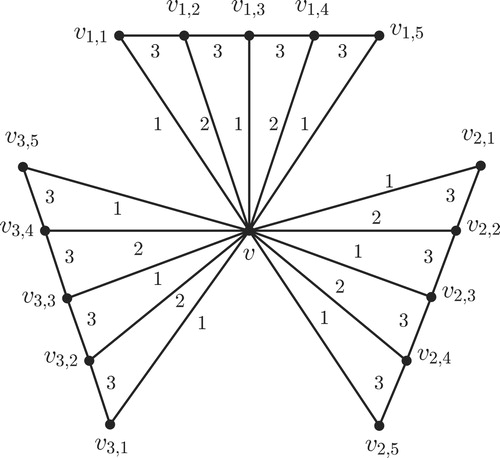
For illustration of Theorems 2.2 and 2.3, see Figs. 1 and 2, respectively.

Next, we consider amalgamation of cycles for any odd and . We show that its rainbow connection number is between lower and upper bounds in Theorem 2.1.

Theorem 2.4

Let and be two positive integers with and . Let where for each , is a cycle . For odd and , .

Proof

We can check that . By similar coloring in Case 1 of Theorem 2.2, we obtain that . Assume to the contrary that . Let

be two sets of colors. We consider three vertices , , and . Since path whose length is connecting each other is unique, the edges of this path must be colored differently. Without loss of generality, let colors that are assigned to edges of sub path are from and edges of sub path are from B. In order we can find a rainbow path, then we must assign colors from B to edges of sub path . So, we need different colors for the edges of path whose length is from to or from to . However, there are only remaining possible colors, producing a contradiction. Thus, and so for odd and . □

Next, we determine the rainbow connection number of amalgamation of either complete graphs, or wheels, or fans respectively in Theorems 2.6^{Theorem 2.7}–2.8. Let be a vertex in a wheel or a fan where the degree of is . Vertex is called the center vertex. We can check that the amalgamation of either wheels or fans has diameter 2 where vertex be the identified vertex of amalgamation of either wheels or fans. Meanwhile, we can also check that the amalgamation of any complete graphs has diameter 2.

The following definitions are taken from [16]. A maximal connected subgraph of is called a component of . Let be a subset of . separates in if subgraph of induced by is disconnected. A vertex which separates two other vertices of the same component is a cut vertex, and an edge separating it ends is a bridge.

The amalgamation of either complete graphs, or wheels, or fans also has a cut vertex, namely the identified vertex . Li et al. [17] obtained upper bounds for rainbow connection number of bridgeless graphs with diameter 2 in the following lemma.

Lemma 2.5

[17]

Let be a bridgeless graph with diameter 2. If has a cut vertex, then .

Now, we provide the rainbow connection number of amalgamation of complete graphs.

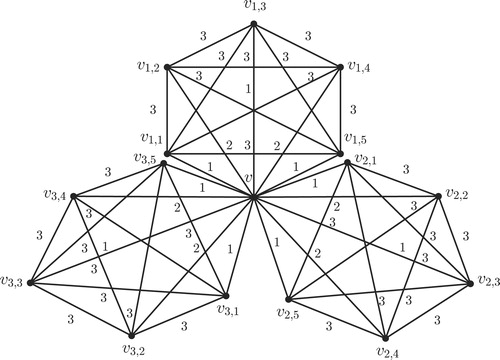
Theorem 2.6

Let and be two positive integers with and . Let where for each is a complete graph . Then

Proof

We define

Proof of upper bound consists of two cases.

Case 1.

=

We define a coloring as follows. where , , and are in with . We can check that there exists a rainbow path between any two vertices in . So, is a rainbow coloring. Thus, for .

Case 2.

=

We define a coloring as follows. where , and are in with . We consider any two vertices . Note that . If , then there exists a rainbow path, namely the edge . Let and for some and in with , and for some and in . Subcase 1. = and have different parity There exists a rainbow path, namely . Subcase 2. = and have same parity There exists a rainbow path, namely for and for . So, is a rainbow coloring. Thus, for .

Hence,

Proof of lower bound consists of two cases.

Case 1.	=	Since , it follows that .
Case 2.	=	Assume to the contrary that . Since , it follows that . Let be a rainbow 2-coloring of . We consider three vertices , , and . Since path whose length is 2 connecting each other is unique, the edges of this path must be colored differently. Without loss of generality, let . In order we can find a rainbow path, then . So, there is no rainbow path between and , a contradiction. Thus, where .

Hence,  □

Next, we provide the rainbow connection number of amalgamation of wheels in the following theorem.

Theorem 2.7

Let and be two positive integers with and . Let where for each , is a wheel with vertices. If for is the center vertex of , then

Proof

We define

Proof of upper bound consists of two cases.

Case 1.

=

and . We define a coloring as follows. where and . We can check that there exists a rainbow path between any two vertices in . So, is a rainbow coloring. Thus, for and .

Case 2.

=

and , or and We define a coloring as follows. where , , and . We can find a rainbow path between any two vertices with the same argument in the proof of upper bound in Case 2 of Theorem 2.6 except for and in the same copies in . If and , then there exists a rainbow path, namely the edge . Let and for some and in with . Subcase 1. = and have different parity There exists a rainbow path, namely . Subcase 2. = and have same parity There exists a rainbow path, namely for and for . So, is rainbow coloring. Thus, for and , or and .

Hence,

Proof of lower bound consists of three cases.

Case 1.	=	and Since ( be the center vertex of ), it follows that .
Case 2.	=	and Assume to the contrary that . By using the same argument in the proof of lower bound of Theorem 2.6 where , we obtain a contradiction. Thus, where .
Case 3.	=	and Assume to the contrary that . Since ( be the center vertex of ), it follows that . Let be a rainbow 2-coloring of . We consider any two vertices and in for some and in with , and for some and in . Since there exists exactly one path whose length is 2 between and , the edges of this path must be colored differently. Without loss of generality, let and . This forces where , and where . Since there is no rainbow path between any two vertices in the same copies of through vertex , it should be through the cycle that is contained in . Subcase 1. = Without loss of generality, let . This forces . It follows that there is no rainbow path connecting and , a contradiction. Subcase 2. = We have . It follows that there is no rainbow path between any two vertices and where , producing a contradiction. Thus, where and .

Hence,  □

The following theorem shows the rainbow connection number of amalgamation of fans.

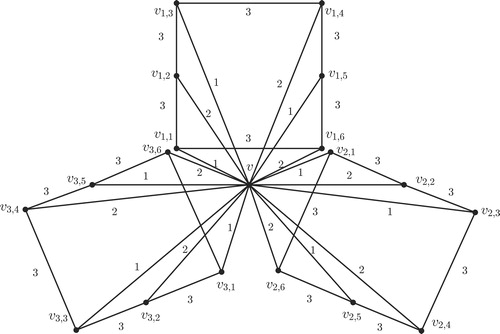
Theorem 2.8

Let and be two positive integers with and . Let where for each , is a fan with vertices. If for is the center vertex of , then

Proof

We define

Proof of upper bound consists of two cases.

Case 1.	=	and . We define a coloring as follows. where . We can check that there exists a rainbow path between any two vertices in . So, is a rainbow coloring. Thus, for and .
Case 2.	=	and , or and We define a coloring as follows. where , , and . We can find a rainbow path between any two vertices with the same argument in the proof of upper bound in Case 2 of Theorem 2.7. So, is a rainbow coloring. Thus, for and , or and .

Hence,

Proof of lower bound consists of three cases.

Case 1.	=	and Since ( be the center vertex of ), it follows that .
Case 2.	=	and Assume to the contrary, that . By using the same argument in the proof of lower bound of Theorem 2.6 where , we obtain a contradiction. Thus, where .
Case 3.	=	and Assume to the contrary that . Since ( be the center vertex of ), it follows that . Let be a rainbow 2-coloring of . We consider any two vertices and in for some and in with , and for some and in . Since there exists exactly one path whose length is 2 between and , the edges of this path must be colored differently. Without loss of generality, let and . This forces where , and where . Since , we obtain that there is no rainbow path connecting any two vertices and where , a contradiction. Thus, where and .

Hence,  □

For illustration of Theorems 2.6^{Theorem 2.7}–2.8, see Figs. 3^{Fig. 4}–5, respectively.

Notes

Peer review under responsibility of Kalasalingam University.