On super edge-magic deficiency of volvox and dumbbell graphs

Peer review under responsibility of Kalasalingam University.

Abstract

Let be a finite, simple and undirected graph of order and size . A super edge-magic total labeling of a graph is a bijection , where the vertices are labeled with the numbers and there exists a constant such that , for every edge . The super edge-magic deficiency of a graph , denoted by , is the minimum nonnegative integer such that has a super edge-magic total labeling, or it is if there exists no such .

In this paper, we are dealing with the super edge-magic deficiency of volvox and dumbbell type graphs.

Keywords:

• Super edge-magic total
• Deficiency
• Cycle
• Volvox
• Dumbbell

1 Introduction

In this paper, we consider finite, simple and undirected graphs. We denote the vertex set and edge set of a graph by and respectively, where and . An edge-magic total labeling of a graph is a bijection , where there exists a constant such that , for every edge . The constant is called the magic constant and a graph that admits an edge magic total labeling is called an edge-magic total graph. An edge-magic total labeling is called super edge-magic total if the vertices are labeled with the smallest possible numbers, i.e. .

Fig. 1 An illustration of graph for and both odd.

Fig. 2 An illustration of graph for even and odd.

Fig. 3 Dumbbell graphs , even cycle.

Fig. 4 Dumbbell graphs , even cycle.

The graph labeling has caught the attention of many authors and many new labeling results appear every year. This popularity is not only due to the mathematical challenges of graph labeling, but also for the wide range of its application, for instance X-ray, crystallography, coding theory, radar, astronomy, circuit design, network design and communication design. In fact Bloom and Golomb studied applications of graph labelings to other branches of science and it is possible to find part of this work in [1] and [2].

The concept of edge-magic total labeling was given by Kotzig and Rosa [3] in 1970. They proved that for any graph there exists an edge-magic total graph such that for some nonnegative integer . This fact leads to the concept of edge-magic total deficiency of a graph [3], which is the minimum nonnegative integer such that is edge-magic total. The edge-magic deficiency of is denoted by . In particular, In the same paper, Kotzig and Rosa gave the upper bound of the edge-magic deficiency of a graph with vertices, where is the th Fibonacci number.

Motivated by Kotzig and Rosa’s concept of edge-magic deficiency, Figueroa-Centeno et al. [4] defined a similar concept for the super edge-magic total labelings. The super edge-magic deficiency of a graph , denoted by , is the minimum nonnegative integer such that has a super edge-magic total labeling, or if there exists no such . More precisely, if then It is easy to see that for every graph , .

In [5,4] Figueroa-Centeno et al. showed the exact values of the super edge-magic deficiencies of several classes of graphs, such as cycles, complete graphs, 2-regular graphs and complete bipartite graphs . They also proved that all forests have finite deficiency. In particular, they proved that

In [6] Ngurah, Simanjuntak and Baskoro proved some upper bound for the super edge-magic deficiency of fans, double fans and wheels. In [7] Figueroa-Centeno et al. proved In the same paper, they proved that They also conjectured that every forest with two components has the super edge-magic deficiency less or equal to 1.

For a positive integer , let be a star with leaves. Lee and Kong [8] use to denote the disjoint union of the stars , . They proved that the following graphs are super edge-magic: where , , , , , , for , , and . They conjectured that is super edge-magic when is odd.

It is known that if a graph with vertices and edges is super edge-magic, then , see [9].

In proving the results in this paper, we frequently use the following proposition.

Lemma 1

[10]

A graph with vertices and edges is super edge-magic total if and only if there exists a bijective function such that the set consists of consecutive integers. In such a case, extends to a super edge-magic total labeling of .

In this paper we are dealing with super edge-magic deficiency of volvox and dumbbell type graphs.

2 Main results

Volvox graphs

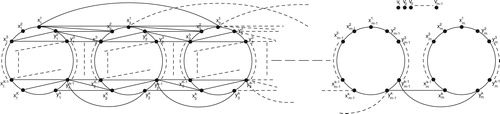
In this section we are dealing with super edge-magic deficiency of volvox graphs. Volvox is one of the best known chlorophytes and is the most developed in a series of genera that forms spherical colonies. Each mature volvox colony is composed of numerous flagellate cells similar to chlamydomonas and embedded in the surface of a hollow sphere or cenobium containing an extracellular matrix made of a gelatinous glycoprotien [11].

For and both are odd, we define the volvox graph as follows, where is the arbitrary number of edges and denotes an isolated vertex. and We have the following theorem.

Theorem 1

For and odd, we have the super edge-magic deficiency of is

Proof

If and then and . Now, define a labeling as follows:

and The set of all edge-sums generated by the above formula forms a consecutive integer sequence . Therefore by Lemma 1, extends to a super edge-magic total labeling with magic constant .  ■

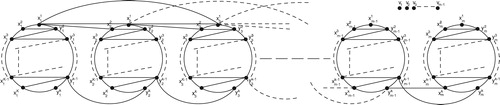
In the next theorem, we are dealing the graph when even and odd. For our convenience, we define the volvox graph as follows: and We have also the following theorem.

Theorem 2

For even and odd, we have

Proof

If and then and . Now, define a labeling as follows:

and The set of all edge-sums generated by the above formula forms a consecutive integer sequence . Therefore by Lemma 1, extends to a super edge-magic total labeling with magic constant .  ■

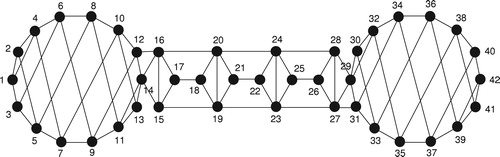
Dumbbell type graphs

In this section we are dealing with super edge magic deficiency of dumbbell type graphs.

Theorem 3

For even, a positive integer, the dumbbell type graph defined as below admits a super edge-magic total labeling. i.e. .

Proof

Let us define the vertex and edge sets of as follows: and

If and then and . Now, define a labeling as follows:

The set of all edge-sums generated by the above formula forms a consecutive integer sequence . Therefore by Lemma 1, extends to a super edge-magic total labeling with magic constant . ■

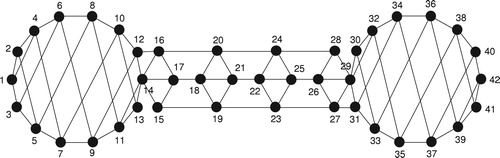
Theorem 4

For even, a positive integer, the dumbbell type graph defined as below has a super edge-magic total labeling. i.e. .

Proof

Let us define the vertex and edge sets of as follows: and  ■

Labeling scheme is same as designed in Theorem 1 (see Figs. 1^{Fig. 2Fig. 3}–4).

Theorem 5

For odd, a positive integer, the dumbbell type graph defined as below admits a super edge-magic total labeling. i.e. .

Proof

Let us define the vertex and edge sets of as follows: and If and then and . Now, define a labeling as follows:

The set of all edge-sums generated by the above formula forms a consecutive integer sequence . Therefore by Lemma 1, extends to a super edge-magic total labeling with magic constant . ■

Theorem 6

For odd, a positive integer, the dumbbell type graph defined as below admits a super edge-magic total labeling. i.e. .

Proof

Let us define the vertex and edge sets of as follows: and Labeling scheme is same as designed in Theorem 3.  ■

3 Concluding remarks

In this paper, we have determined an upper bound for super edge-magic deficiency of volvox graphs. We have also determined the exact value of super magic deficiency of some dumbbell type graphs. We encourage the researchers to try to determine the super edge-magic deficiency of other graphs for further research. In fact, it seems to be a very challenging problem to find the exact value for the super edge-magic deficiency of families of graphs.

Notes

Peer review under responsibility of Kalasalingam University.