Abstract
A graph on vertices is said to admit a prime labeling if we can label its vertices with the first
natural numbers such that any two adjacent vertices have relatively prime labels. Here we extend the idea of prime labeling to the Gaussian integers, which are the complex numbers whose real and imaginary parts are both integers. We begin by defining an order on the Gaussian integers that lie in the first quadrant. Using this ordering, we show that several families of trees admit a prime labeling with the Gaussian integers.
1 Introduction
A graph on vertices admits a prime labeling if its vertices can be labeled with the first
natural numbers in such a way that any two adjacent vertices have relatively prime labels. Many families of graphs are known to admit prime labelings — such as paths, stars, caterpillars, complete binary trees, spiders, palm trees, fans, flowers, and many more [Citation1,Citation2]. Entringer conjectured that any tree admits a prime labeling, however this conjecture is still open in general. In this paper we extend the study of prime labelings to the Gaussian integers.
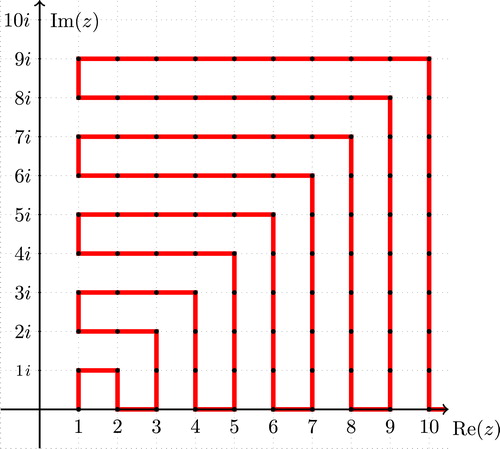
In order to extend the notion of a prime labeling to Gaussian integers, we must first define what we mean by “the first Gaussian integers”. In Section 2, we define a spiral ordering on the Gaussian integers that allows us to linearly order the Gaussian integers. This spiral ordering preserves many familiar properties of the natural ordering on
. For example, the spiral ordering alternates parity, and consecutive odd integers in the spiral ordering are relatively prime. We discuss further properties of the spiral ordering in Section 2. In Section 3, we apply the properties of the spiral ordering to prove that several families of trees admit a prime labeling with the Gaussian integers under the spiral ordering.
2 Background and definitions
2.1 Background on the Gaussian integers
We begin with some relevant background on Gaussian integers to provide a foundation for our work.
The Gaussian integers, denoted , are the complex numbers of the form
, where
and
. A unit in the Gaussian integers is one of
. An associate of a Gaussian integer
is
where
is a Gaussian unit. The norm of a Gaussian integer
, denoted by
, is given by
. A Gaussian integer is even if it is divisible by
and odd otherwise. This is because Gaussian integers with even norms are divisible by
.
Definition 2.1
A Gaussian integer is prime if its only divisors are
,
,
, or
.
Besides this definition of Gaussian primes, we have the following characterization theorem for Gaussian primes. Further information on the Gaussian integers can be found in Rosen’s Elementary Number Theory [Citation3].
Theorem 2.2
A Gaussian integer is prime if and only if either
| • |
| ||||
| • |
| ||||
| • |
| ||||
Definition 2.3
Let and
be Gaussian integers. We say
and
are relatively prime or coprime if their only common divisors are the units in
.
2.2 Prime labelings of graphs with the Gaussian integers
Throughout this paper we consider finite graphs without loops or multiple edges, and in particular we will study trees. We write to denote an edge in a graph connecting vertex
to vertex
. For trees, we say that a vertex is a leaf or endvertex if it has degree 1 and that it is an internal node otherwise.
Our goal is to extend the study of the prime labeling of trees to the Gaussian integers. Because the Gaussian integers are not totally ordered, we must first give an appropriate definition of “the first Gaussian integers”. We propose the following ordering:
Definition 2.4
The spiral ordering of the Gaussian integers is a recursively defined ordering of the Gaussian integers. We denote the th Gaussian integer in the spiral ordering by
. The ordering is defined beginning with
and continuing as:
This is illustrated in .
Under this ordering, the first 10 Gaussian integers are and we write
to denote the set of the first
Gaussian integers in the spiral ordering.
We exclude the imaginary axis to ensure that the spiral ordering excludes associates. Consecutive Gaussian integers in this ordering are separated by a unit and therefore alternate parity, as in the usual ordering of . However, several properties of the ordinary integers do not hold. In the set of the first
numbers, (
), it is not guaranteed that there are exactly
multiples of
(or any other residue class mod
). Furthermore, odd integers with indices separated by a power of two are not guaranteed to be relatively prime to each other.
This definition of the spiral ordering for the Gaussian integers leads to the following definition of prime labeling of trees with Gaussian integers.
Definition 2.5
Let be a graph on
vertices. A Gaussian prime labeling of
is a bijection
such that if
, then
and
are relatively prime; that is, neighboring vertices have relatively prime labels.
2.3 Properties of the spiral ordering
We define several pieces of the Gaussian spiral ordering. Corners of the spiral ordering occur when the spiral turns from north to east or east to north, from south to east or east to south, or from north to west or west to north. Branches of the spiral occur when the spiral travels along a straight path going north, south, east, or west. Steps along the real axis and the line are not counted as branches.
Our first goal is to determine the index of an arbitrary Gaussian integer, , in the spiral order based on which type of branch or corner it lies on. We use
to denote the index of
in the spiral ordering. First note that there are three types of corners:
| • | real corners at Gaussian integers on the real axis, | ||||
| • |
| ||||
| • | interior corners at Gaussian integers on the line | ||||
Similarly the branches come in four types:
| • | up-oriented branches, which contain Gaussian integers between odd corners on the real axis and interior corners, | ||||
| • | down-oriented branches, which contain Gaussian integers between interior corners and even corners on the real axis, | ||||
| • | right-oriented branches, which contain Gaussian integers between even corners on the | ||||
| • | left-oriented branches, which contain Gaussian integers between interior corners and odd corners on the | ||||
Lemma 2.6
Corners in the spiral ordering lie on either the real axis, the line, or the line
. Their indices are found as follows:
Proof
Observe that Gaussian integers of the form , with
even, or
, with
even, are the corner nodes in squares composed of
or
nodes respectively. The spiral-ordering path will pass through each of these nodes once and will end on an even corner on the real axis if the number of nodes is even, and an odd corner on the
line if the number of nodes is odd. Therefore, the index of an even corner on the real or an odd corner on the
line will be the number of nodes in that square.
Odd corners on the real axis and even corners on the line will always have the index following the corresponding even corners of the real axis and odd corners on the
line.
The interior corners are of the form . If
is even, then the corner is
nodes before an odd corner on the
line. If
is odd, the corner is
nodes before an even corner on the
line. In either case, since
, the index of the corner will be
. ■
Theorem 2.7
Let be a Gaussian integer with
and
. Then its index in the spiral ordering,
, is given by the following formula:
Proof
Each branch references the corners of the spiral ordering. If lies on an up-oriented branch, then
is odd. Consider the odd corner on the real axis at
. By Lemma 2.6, the index of this corner is
. Therefore the index of
is
.
If lies on a left-oriented branch, then
is even. Consider the odd corner on the
line at
. By Lemma 2.6, the index of this corner is
. Therefore the index of
is
.
If lies on a right-oriented branch, then
is odd. Consider the even corner on the
line at
. By Lemma 2.6, the index of this corner is
. Therefore the index of
is
.
If lies on a down-oriented branch, then
is even. Consider the even corner on the real axis at
. By Lemma 2.6, the index of this corner is
. Therefore the index of
is
. ■
Now that we have a formula for the index of a Gaussian integer in the spiral ordering, we prove several lemmas about Gaussian integers that will be useful in proving that various families of trees have Gaussian prime labelings.
Lemma 2.8
Let be a Gaussian integer and
be a unit. Then
and
are relatively prime.
Proof
Suppose that there exists a Gaussian integer such that
and
. This means that
must also divide
. But the only Gaussian integers that divide
are the units, so
must be a unit. Thus
and
are relatively prime. ■
The following corollary is immediate because consecutive Gaussian integers in the spiral ordering have a difference of one unit.
Corollary 2.9
Consecutive Gaussian integers in the spiral ordering are relatively prime.
Lemma 2.10
Let be an odd Gaussian integer, let
be a positive integer, and let
be a unit. Then
and
are relatively prime.
Proof
Suppose that and
share a common divisor
. It follows that
divides
. However, the only divisors of
in
are all powers of
and its associates and the units in
. Since
is odd, it is not divisible
or its associates because those numbers are all even. Therefore,
must be a unit. Hence
and
are relatively prime. ■
Corollary 2.11
Consecutive odd Gaussian integers in the spiral ordering are relatively prime.
Proof
Consecutive odd Gaussian integers in the spiral ordering differ by two units. The only possible differences between them are therefore , 2, or one of their associates. Since
, all of these differences are of the form
so the result follows from Lemma 2.10. ■
Lemma 2.12
Let be a Gaussian integer and let
be a prime Gaussian integer. Then
and
are relatively prime if and only if
.
Proof
Assume that there exists a Gaussian integer such that
and
. Then
must also divide
. But
is prime, so either
or
for some unit
. If
, then
and
have a common factor of
and are not relatively prime. If
is a unit, then
and
have only a common factor of a unit and are relatively prime. Therefore
and
are relatively prime if and only if
. ■
Lemma 2.13
Let be a prime integer congruent to
and let
be a Gaussian integer such that
. Then the index of
in the spiral ordering is congruent to 0 or
.
Proof
By Theorem 2.2, is prime in
, so if
, then
and
. So
. From Theorem 2.7, we can calculate the index
of
and examine it modulo
. There are four cases to consider. In Case 1,
. In Case 2,
. In Case 3,
. In Case 4,
. Therefore
or
for any
such that
. ■
3 Results for families of trees
We can now use the properties of the spiral ordering from the previous section to construct a Gaussian prime labeling for several classes of trees. For each class of tree considered, we will give a definition, an example figure, and then provide our proof of the existence of a Gaussian prime labeling. We consider stars, paths, spiders, -centipedes,
-double stars,
-centipedes, and
-firecrackers.
3.1 Results on stars, paths, spiders,  -centipedes, and
-centipedes, and  -double stars
-double stars
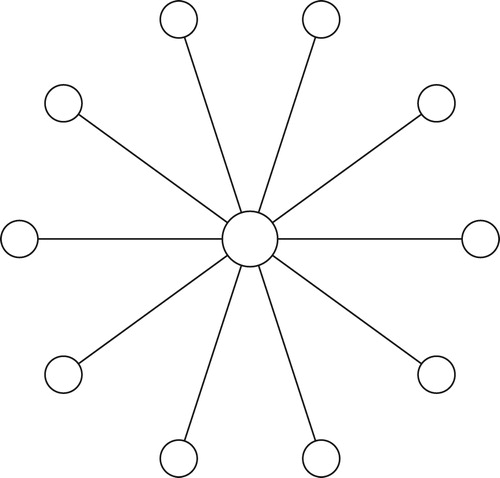
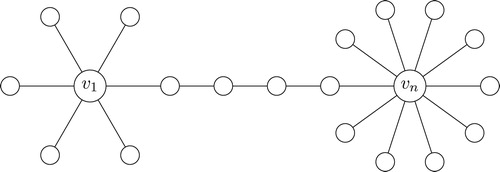
Definition 3.1
The star graph, , on
vertices is the graph with (see )
Theorem 3.2
Any star graph admits a Gaussian prime labeling.
Proof
Label vertex with
. The center vertex
is then labeled with
, which is relatively prime to all Gaussian integers. Therefore this is a Gaussian prime labeling. ■
Definition 3.3
The path graph, , on
vertices is the graph with (see )
Theorem 3.4
Any path admits a Gaussian prime labeling.
Proof
Label vertex with
. By Corollary 2.9 consecutive Gaussian integers in the spiral ordering are relatively prime, so this is a prime labeling of the path. ■
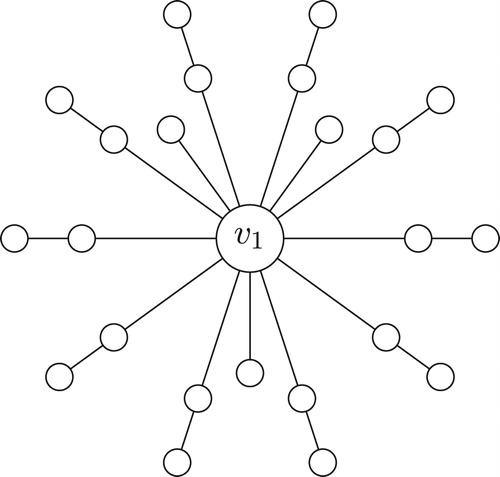
Definition 3.5
A spider graph is a tree with one vertex of degree at least 3 and all other vertices having degree 1 or 2 (see ).
Theorem 3.6
Any spider tree admits a Gaussian prime labeling.
Proof
Let be a spider tree and suppose the center vertex
has degree
. Then if we remove
from
we are left with paths
with lengths
respectively. So label
with 1 and label
with the next
consecutive Gaussian integers
, then label
with the next
consecutive Gaussian integers, and so on. By Corollary 2.9 this is a Gaussian prime labeling. ■
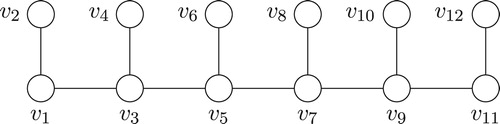
Definition 3.7
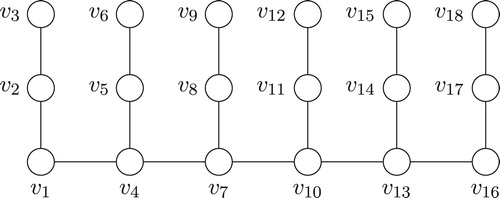
The -centipede tree,
, is the graph with (see )
and
Theorem 3.8
Any -centipede tree admits a Gaussian prime labeling.
Proof
Label vertex with
. This is a Gaussian prime labeling because consecutive Gaussian integers in the spiral ordering are relatively prime by Corollary 2.9 and consecutive odd Gaussian integers in the spiral ordering are relatively prime by Corollary 2.11. ■
Definition 3.9
Let be integers with
. The
-double star tree,
, is the graph with
and
In the -double star tree we have a path of length
whose endvertices
and
are the central vertices for stars on
and
vertices respectively (not including the other vertices on the path) (see ).
Theorem 3.10
Any -double star tree has a Gaussian prime labeling.
Proof
Label with
,
with
, and
with the consecutive Gaussian integers
. We now label the
remaining vertices adjacent to
with odd Gaussian integers. If
is odd, label
with
. If
is even, label
with
. Label the remaining vertices adjacent to
arbitrarily with the remaining Gaussian integers in
. This is a Gaussian prime labeling because
is relatively prime to all odd Gaussian integers, 1 is relatively prime to all Gaussian integers, and the path is labeled with consecutive Gaussian integers. ■
Note that when , this is a star graph and when
it is a path. When
and
, it is a firecracker graph.
3.2 Results on  -centipede trees
-centipede trees
Definition 3.11
The -centipede tree,
, is the graph with
and
Before we prove a result about -centipede trees, we will prove a lemma about Gaussian integers whose indices are three places apart in the spiral ordering.
Lemma 3.12
Let with
, and consider the Gaussian integers
and
. Then
, and each of these values of
does arise for some
.
Proof
In the spiral ordering, Gaussian integers whose indices differ by 3 are three units apart. The possible combinations of three units are , and their associates. First, we know that the orientation of the spiral ordering will rule out
, and
. If
and
lie on the same branch, then they differ by
or
. Otherwise there is a corner between them and we consider three possibilities:
and
are separated by a corner on the real axis,
and
are separated by a corner on the line
, or
and
are separated by an interior corner.
Around corners on the real axis, we know is of the form
,
, or
for some even integer
. If
, by Theorem 2.7, we know its index is
which is not congruent to
. Therefore
. If
, then by Theorem 2.7 we know that
which is possible when
. In this case
, so
. If
, by Theorem 2.7, we know that
which is possible when
. In this case
, so
. The possible values of
for corners on the real axis are thus 1 and
.
Around corners on the line , we know that
is of the form
, or
for some even integer
or else
and
would lie on the same branch. If
, by Theorem 2.7 its index would be
, which is not congruent to
. Therefore
. If
, then Theorem 2.7 says that
, which is possible when
. In this case
and so
. If
, then Theorem 2.7 says that
, which is possible when
. In this case
and so
. The possible values of
for corners on the line
are thus
and
.
Around interior corners there are two possible orientations. Either the spiral is moving from an up-oriented branch to a left-oriented branch or the spiral is moving from a right-oriented branch to a down-oriented branch. First, consider the up-left interior corner. We know has the form
or
as
and
would lie on the same branch otherwise.
If , Theorem 2.7 says that
which is possible when
. In this case
and so
.
If , Theorem 2.7 says that
; or, equivalently, that
. This is possible when
or
. In this case
and so
.
By symmetry, the possible values for a right-down interior corner are
and
. ■
Lemma 3.13
Let with
and consider the Gaussian integers
and
. Let
. If
, then
must be odd.
Proof
First suppose . This happens only when
and
; i.e., the spiral turns at the line
. By Theorem 2.7,
is even and
is even. Thus
must be odd.
Next, suppose . There are two scenarios in which this can happen. First, as the spiral makes a right-to-down turn around an interior corner; and second, as the spiral makes a down-to-right turn at the real axis. In the former case,
. By Theorem 2.7,
is even. Therefore
is odd. In the latter case,
for some even
. By Theorem 2.7,
is even. Once again,
must be odd. ■
Theorem 3.14
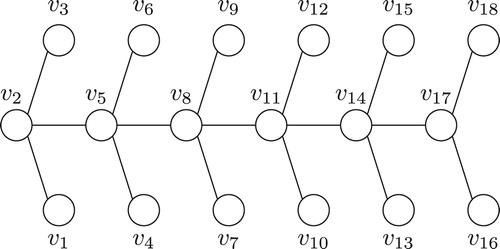
Any -centipede tree admits a Gaussian prime labeling.
Proof
Begin by labeling vertex with
. We call the set of nodes
which have degree greater than one the spine of the tree, and the other nodes the leaves. Each spine–leaf pair in the same segment will be relatively prime because they are labeled by consecutive Gaussian integers, but there will be adjacent nodes down the spine that are not relatively prime.
Consider the possible separations of pairs of nodes on the spine. Let . By Lemma 3.12,
. This presents a problem whenever
is not a unit, but it divides both
and
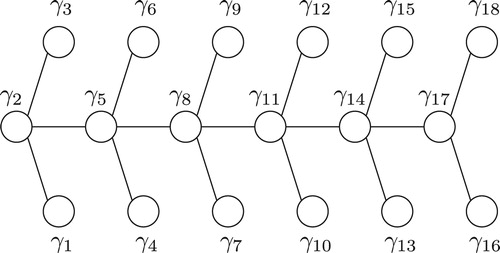
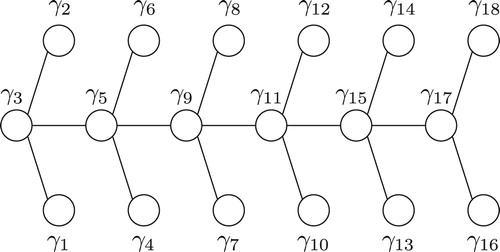
. To solve this problem, we will swap the labels of some spine nodes with the labels of one of their leaf neighbors (see ).
Specifically, we swap each even on the spine with its neighboring leaf
and consider the new labeling. In each segment of the caterpillar where a swap occurred, the node on the spine is consecutive to one of its leaves and a consecutive odd to the other one. Thus, by Corollaries 2.9 and 2.11, the node on the spine is relatively prime to its adjacent leaves (see ).
Now we verify that the labels of the nodes along the spine are relatively prime. Along the spine, we will have a sequence of odd Gaussian integers with indices . Every pair of adjacent vertices along the spine are either consecutive odd Gaussian integers or odd Gaussian integers whose indices differ by four. In the former case, the labels are relatively prime by Corollary 2.11. We claim that the labels in the latter case are also relatively prime.
Let and
be a pair of neighboring vertices on the spine whose indices differ by four. We assume
is the vertex that was originally unswapped, while
is the vertex that was swapped onto the spine. Therefore, the index
is odd, which means
is even.
As before, consider the difference and
. By Lemmas 3.12 and 3.13,
. We examine each of these possibilities separately.
If , then it follows from Theorem 2.7 that
. For example, when
,
and
are situated on a right-oriented branch. So
equals either 4 or
. If
, then
for some odd
. Therefore, by Theorem 2.7,
. On the one hand,
is even so
is even. On the other hand,
is odd, so
is odd, a contradiction. Therefore,
. The proofs of the remaining cases follow similarly.
If , then
because
only when the spiral turns as it meets the real axis. If
, then
because
when the spiral makes a right-to-down turn at an interior corner.
If , then either
(as the spiral turns at the
line) or
(as the spiral makes an up-to-left turn at an interior corner). However, the latter case is impossible. In that case
, so by Theorem 2.7,
, which is even. But
is even so
is odd, a contradiction. Therefore, when
, we have
.
Finally, if , the spiral makes an up-to-left turn at an interior corner and hence
.
In summary, we have concluded that . Up to multiplication by a unit, each of these values
is a power of
. Thus by Lemma 2.10, the odd labels along the spine are all relatively prime. Therefore, we have achieved a prime labeling of the
-centipede. ■
3.3 Results on  -firecracker trees
-firecracker trees
The proof that -caterpillar trees admit a Gaussian prime labeling relied on an initial natural labeling that was slightly modified to give a prime labeling. In this section we use a similar technique to show that certain firecracker trees also admit prime labelings.
Definition 3.15
The -firecracker tree,
is the graph with (see )
and
We call the vertices
the spine of the tree. The set of vertices
for some
is called the
th level of the tree.
Lemma 3.16
Let be a Gaussian integer. Then
if and only if
and
if and only if
.
Proof
Suppose . Then
. Hence
. Conversely, suppose
such that
. It follows that
so
, and
. Therefore
, so
, and
. Hence
.
The argument for is similar. ■
This lemma is illustrated in , which shows the mod 5 residues of a multiple of or
.
Table 1 Components of multiples of  and
and  reduced modulo 5.
reduced modulo 5.
Lemma 3.17
For , let
and assume that
is not a unit. If
and
then one of the following six conditions holds:
| (1) |
| ||||
| (2) |
| ||||
| (3) |
| ||||
| (4) |
| ||||
| (5) |
| ||||
| (6) |
| ||||
Proof
First, by Lemma 2.13 is not equal to 3 or one of its associates. Because
and
are three indices apart in the spiral ordering and
is not
, or any of their associates,
must be
,
, or one of their associates. We also know that
by the orientation of the spiral ordering. Now we consider the remaining associates according to the location of
in the spiral ordering.
Case 1: Interior corners on up-left branches. This case corresponds to or
. If
, then
for some odd
because it is one step below the interior corner
. Then Theorem 2.7 says that its index is
, which is always congruent to 0 or 2 mod 3. This contradicts that the index is
. Therefore this
does not occur.
If , then by Theorem 2.7
for some odd
because it is two steps below the interior corner
. Using we see that we must have
for this to occur.
Case 2: Interior corners on right-down branches. This case corresponds to or
. If
, then
for some
because it is one step left of the interior corner
. Theorem 2.7 says that its index is
, which is always congruent to 0 or
. Again this contradicts that the index is
. So this
does not occur.
If , then by Theorem 2.7
for some even
because it is two steps left of the interior corner
. Using we see that we must have
for this to occur.
Case 3: Corners on the real axis. This case corresponds to or
. If
then
and
for some odd
(by Theorem 2.7) with
(by ).
If , then
and
for some even
(by Theorem 2.7) with
(by ).
Case 4: Corners on the line . This case corresponds to
or
. If
, then by Theorem 2.7
for some even
because it is 2 away from the corner on the
line at
. Using we see that we must have
for this to occur.
If , then by Theorem 2.7
for some even
because it is a corner on the
line. Using we see that we must have
for this to occur. ■
Theorem 3.18
Any -firecracker tree has a Gaussian prime labeling.
Proof
A natural first attempt at labeling the -firecracker is to label it consecutively by labeling
with
for all
. This is a nearly prime labeling, so we make a handful of swaps of labels to resolve the issues that appear and give a fully prime labeling. The full labeling procedure is as follows.
We define an initial labeling of the
-firecracker so that
. Now we define a new labeling
in the following way. Let
. Consider each
where
is not a unit,
, and
. By Lemma 3.17 we know that
. If
, or
, then we set
and
. If
, then we set
and
. If
, then we set
,
,
, and
. For all other
, keep
.
Because the effect of each above change is to swap the labels of vertices at the ends of a particular level, adjacent vertices on the same level are still labeled with consecutive Gaussian integers in the spiral ordering, which are relatively prime. Therefore, we only need to show that this new labeling has created a prime labeling on the spine. To show the vertices along the spine are now relatively prime, we examine each edge along the spine. If neither vertex incident to a given edge is affected by the relabeling, then the labels are relatively prime. Otherwise we must inspect each relabeled vertex to make sure its new label is relatively prime to its neighbors on the spine. To do this, we consider each in turn. Note that the conditions from Lemma 3.17 force
to be large enough that if
and
then
and
are on the same branch and
and
are on the same branch and so neither
or
was relabeled.
If , then
. By Lemma 3.17
lies at an interior corner
with
. Since
and
are relatively prime, we need only check whether
and
are relatively prime. Then
, so their only possible common factors are unit multiples of
and
. Consulting , we see that because
and
neither
or
divides
and so
and
are relatively prime.
If , then
. Note that
lies at an interior corner
for some
by Lemma 3.17. Here
, so the only possible common factors are again unit multiples of
and
. Consulting , we see that because
and
neither
nor
divides
and thus
and
are relatively prime.
If then
for some odd
and
. Since
and
are consecutive, they are relatively prime and we need only consider the new
. So
and
are also relatively prime.
If , then
for some even
and
. Since
and
are consecutive, they are relatively prime and we only consider the new
. Because
is a multiple of both
and
, it follows that
is not divisible by
or
. So
and
are relatively prime.
If , then
for some
. Since
and
are consecutive, they are relatively prime and we need only look at
. Consulting , we see that because
and
neither
or
divides
. So
and
are relatively prime.
If , then
for some
. We also have
, and
. We now have the sequence of labels on the spine of
. First,
and
are consecutive and thus relatively prime. Also,
and
have a difference of
and are thus relatively prime. Finally,
. Consulting we see that because
and
neither
or
divides
, so
and
are also relatively prime.
Thus is a prime labeling of the
-firecracker tree. ■
4 Future work and open problems
We conclude with a few open problems and directions for future research.
| (1) | A binary tree is a rooted tree in which each node has at most two children. There are many special classes of binary trees, such as full binary trees, perfect binary trees, or complete binary trees. Investigate Gaussian prime labelings of these families of trees. | ||||
| (2) | Investigate Gaussian prime labelings of general | ||||
| (3) | Investigate Gaussian prime labelings of families of non-tree graphs. | ||||
| (4) | In a recent paper [Citation4], the second and third authors showed that trees on at most 73 vertices admit Gaussian prime labelings. The approach outlined in that paper pushed the limits of what one could possibly hope to do by hand. Is it possible to computationally verify the conjecture for trees on more vertices? | ||||
| (5) | Investigate other inherent properties of the spiral ordering on the Gaussian integers. In what ways is it similar to the properties of the order on the natural numbers and in what ways is it different? | ||||
Notes
Peer review under responsibility of Kalasalingam University.
References
- Joseph A.GallianA dynamic survey of graph labelingElectron. J. Combin.21201443 Dynamic Survey 6 (electronic)
- LeanneRobertsonBenSmallOn Newman’s conjecture and prime treesIntegers9A102009117128
- K.H.RosenElementary Number Theory and Its Applications2011Addison-Wesley
- HunterLehmannAndrewParkPrime labeling of small trees with the Gaussian integersRose-Hulman Undergrad. Math J.2015 Preprint available: http://fac-staff.seattleu.edu/klees/web/SmallTrees.pdf, in press