Abstract
In Bagga et al. (1995) a generalization of the line graph concept was introduced. Given a graph with at least
edges, the super line graph of index
,
, has as its vertices the sets of
edges of
, with two adjacent if there is an edge in one set adjacent to an edge in the other set. The line completion number
of a graph
is the least index
for which
is complete. In this paper we investigate the line completion number of
. This turns out to be an interesting optimization problem in number theory, with results depending on the parities of
and
. If
and
is a fixed even number, then
has been found for all even values of
and for all but finitely many odd values. However, when
is odd, the exact value of
has been found in relatively few cases, and the main results concern lower bounds for the parameter. Thus, the general problem is still open, with about half of the cases unsettled.
1 Introduction
The line graph of a graph is arguably the most important and best loved of graph operations, and so not surprisingly mathematicians have taken pleasure in generalizing it in many ways. In forming the line graph of a graph , one takes the individual edges of
as the vertices of the new graph
, with two joined if they have a common vertex, as illustrated in .
In most generalizations of line graphs, the vertices of the new graph are taken to be another family of subgraphs of , and adjacency is defined in terms of an appropriate intersection. For example, in the
-path graph
, the vertices are the paths in
of length
, with adjacency being defined as overlapping in a path of length
. shows the 2-path graph operation.
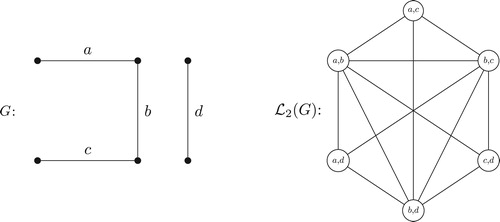
In Bagga, Beineke, and Varma [Citation1], a different choice was made, one that has turned out to yield many interesting results. Given a graph with at least
edges, the super line graph (of index
)
has as its vertices the sets of
edges of
, with two adjacent if there is an edge in one set adjacent to an edge in the other set. An example of a super line graph of index 2 is shown in .
For convenience, in the remainder of this article we adopt the convention that when we speak of a super line graph of index
, the base graph
has at least
edges. Other notation conventions that we adopt are the following:
denotes the edge-order of
(the number of edges in the graph
);
denotes the subgraph induced by a nonempty subset
of the vertices of
; and
denotes the union of disjoint graphs
and
, with
denoting the graph consisting of
copies of
.
1.1 Index 2
Not surprisingly, the super line graphs of index 2 have attracted the greatest interest, and in this subsection, we give a brief survey of some of the results on this family, beginning with a couple of observations [Citation2] about two pairs of edges and
in a graph
that are not adjacent in
:
| (a) | In the graph of the union of the two pairs, the intersection is either empty or an isolated edge. | ||||
| (b) | If neither | ||||
Consequently, we have the following result.
Theorem 1.1
If has at most one isolated edge, then the diameter of
is 1 or 2.
Some other interesting results on this family of graphs involve Hamiltonian properties; for example, it has been shown that (see Bagga, Beineke, and Varma [Citation3] and Li, Li, and Zhang [Citation4]) if is connected, then
is vertex-pancyclic and path-comprehensive (that is, every pair of vertices are joined by paths of all lengths greater than 1).
One area of investigation in the study of line graphs themselves is to find all those graphs whose line graph has a specified property. For example, in considering the property of completeness, the only connected graphs whose line graphs are complete are the stars and the complete graph
. The following result [Citation2] tells when the super line graph of index 2 is complete.
Theorem 1.2
The super line graph of index 2 of a connected graph with at least two edges is complete if and only if it does not contain either or
as a subgraph.
Of course, most graphs contain such a subgraph; for instance, any graph having a path of length 5 does. However, as we shall see, for any graph there are indices for which the super line graph is complete, the topic we turn to next.
1.2 The line completion number
This subsection is devoted to the topic that gave rise to our consideration of the subject of the paper: the line completion number of a graph. Before getting to that, we provide some general results on subgraphs of super line graphs (see [Citation1] and [Citation5]).
Theorem 1.3
For all graphs and all
,
has at most one nontrivial component.
Theorem 1.4
If is a subgraph of
with at least
edges, then
is an induced subgraph of
.
Theorem 1.5
If is a graph with
edges, then for
,
is isomorphic to a subgraph of
.
We noted earlier that unless two components of a graph are single edges, then
has diameter 1 or 2, and so, loosely speaking, it does not “spread out” much. A similar statement holds for higher indices: If no more than
components of
are single edges, then
has diameter 1 or 2.
Theorem 1.6
For any graph , if
is complete, then so is
.
It follows from this result that there is a least index for which the super line graph of a graph is complete, and thus all those of greater index are also complete. Formally, we have this definition: The line completion number of a graph
is the least index
for which
is complete.
The first of the next two results (see [Citation5]) gives those graphs whose line completion number is small, while the second gives those for which it is as large as possible.
Theorem 1.7
Let be a graph.
| • |
| ||||
| • |
| ||||
| • |
| ||||
Theorem 1.8
Let be a graph with
edges.
| • |
| ||||
| • |
| ||||
The following theorem gives a sharp upper bound for the line completion number in terms of the order and number of components.
Theorem 1.9
If is a graph with
edges and
components, then
Furthermore, this bound is sharp for all
and
.
In the remainder of the paper, we are interested only in connected graphs, and for these we have this result:
Corollary 1
If is a connected graph with
edges, then
This bound is sharp for all
.
Turning to lower bounds, as we noted earlier, if and
are two sets of
edges having no vertices in common, then the corresponding vertices are not adjacent in
. Consequently, we have the next result.
Lemma 1
For any graph ,
where the maximum is over all sets
for which
.
These two bounds have been very useful in establishing other results. For example, we have the following theorem on trees.
Theorem 1.10
If is a tree of order
, then
. Furthermore, for any integer
satisfying
, there exists a tree of order
and line completion number
.
The bounds have also been useful in determining the line completion number of the graphs in several common families of graphs. Here, as usual, and
denote the path and cycle of order
, respectively. Also, the fan
, the wheel
, and the windmill
are the graphs resulting from adding one vertex adjacent to all of the vertices in the path
, the cycle
, and the graph
, respectively.
Theorem 1.11
| • | Complete graphs: | ||||
| • | Paths and cycles: | ||||
| • | Fans and wheels: | ||||
| • | Windmills: | ||||
Notably absent from these results is the family of complete bipartite graphs , — and that problem is the subject of this paper. Because of the structure of complete bipartite graphs, it turns out the lower bound of Lemma 1 is important. Since every induced subgraph of a complete bipartite graph is also complete bipartite, this observation can be restated as follows:
It is therefore useful to have this notation:
where the maximum is taken over all
and
with
and
.
Thus, since , the line completion number of complete bipartite graphs boils down to a purely combinatorial problem, and that is the approach we take here. Hence, in the remainder of the paper, the problem that we concentrate on is simply this:
Find for positive integers
and
.
We first considered this problem some years ago, and realized then that it was unlikely to have a simple solution. Gutiérrez and Lladó [Citation6] showed that for all and
,
(which we had also observed) and conjectured that
and that
when
. As we show, when one of
and
is odd and the other even, their conjecture does not always hold. However, for a given even value of
, this is the case for only a finite number of odd values of
. On the other hand, when
and
are both odd, their conjecture almost never holds, and in fact can be off by an arbitrarily large amount.
2 Results
It is not surprising that the answer to our question depends on the parities of and
, and we consider separately the four possible combinations of odd and even values of
and
with
:
| • | Type I: Both | ||||
| • | Type II: Both | ||||
| • | Type III: | ||||
| • | Type IV: | ||||
While the first case is simple (we show that ), the other three are more complicated, and therefore more interesting, and in fact we have been unable to find a complete solution in any of those cases. One noteworthy difference between them is what happens in the long run. If
is even and
is odd, then (as we shall show) for fixed
,
holds for all but finitely many values of
. However, if both are odd, then there is no comparable formula.
Before considering the four types individually, we introduce a bit more notation and terminology. Given and
, we let
and
(thus,
or
and
or
, depending on their parity). We define the base case for each of the four types:
| • | Type I: For | ||||
| • | Type II: For | ||||
| • | Type III: For | ||||
| • | Type IV: For A pair | ||||
It is easily seen that within each of the four types the product of the two numbers in the base case gives a lower bound for . One question that we consider is when does equality hold; that is, when is the base case optimal.
2.1 Type I
The solution for this type is straightforward: we simply split each number in half.
Theorem 2.1
If and
, then
.
Proof
If , then there must exist
for which both
and
, and this is easily seen to be impossible. ■
2.2 Type II
We now turn to the situation with both and
odd,
and
with
, and the base case is the pair
with product
. Most of our results in this section concern the question of whether the base case holds or not. In general, when the base case does not hold, finding the exact value seems difficult. Therefore, our results usually involve either finding a split of
and
that does better than the base case or showing that no better split exists.
We observe that when the base case does not hold, that is, when , there exist non-negative integers
and
for which both
and
exceed
:
(1) and
(2) It follows from (Equation1
(1) ) that
(3) and similarly from (Equation2
(2) ) that
(4)
We note that if , then, taken together, (Equation3
(3) Equation4
(4) ) imply that
, so
. It is convenient to split this type into two sub-types along these lines; that is,
Type II(a): ,
Type II(b): .
In terms of and
, in Type II(a),
, and in Type II(b),
.
2.2.1 Type II(a)
shows that sometimes the base case holds and sometimes it does not. The values for in were determined with a computer program that we developed. The values in bold are those where the base case does not hold. Our computer program verified that the smallest pair
of Type II(a) for which the base case is not optimal has
and
, for which
. For the remainder of Section 2.2.1 we assume that
. (In Section 2.2.2 we will prove that the base case does not hold for Type II(b).)
Table 1 Several values for Type II(a): Both  and
and  odd,
odd,  .
.
We first show that for given there are five values of
at the upper end of the range for which the base case is optimal.
Theorem 2.2
If and
and
, then for
, the base case holds, that is,
. Furthermore, these bounds on
are sharp.
Proof
Suppose not. For convenience, we let (so
). Then it follows from (Equation3
(3) ) that
and since the last fraction is positive for
and
must be an integer,
Likewise, (Equation4
(4) ) implies that
and so, by similar reasoning, since
,
Since the two bounds on
are inconsistent, the result follows.
Now consider the case . It is straightforward to check that both of the products
and
exceed
(in the above notation,
and
). Thus, the base case does not hold. Similarly, for
, the products
and
exceed
(here
and
). Thus, both bounds are sharp. ■
We note that the base case also holds when is relatively close to
.
Theorem 2.3
With and
, if
, then the base case holds.
Proof
Suppose not. Then there exist and
satisfying (Equation3
(3) Equation4
(4) ). Since
, it follows from our remark above that
. From (Equation3
(3) Equation4
(4) ) it follows that
Letting , we get, upon simplification,
It follows that since ,
which contradicts the bound on
in the hypothesis. ■
We now look a bit further at what this theorem tells us about the greatest value of
for which the base case holds for
. Our data show that
for
. However,
, and, as noted earlier, the smallest pair
of Type II(a) for which the base case is not optimal has
and
, for which
. In fact, as a special case of the next theorem, we see that the base case is not optimal for
and
.
Based on small values (up to ), we thought it reasonable to conjecture that the least value of
for which the base case does not hold has
and
, whence
. However, this is not the case, with the least counterexample being for
and
, with
and
. (It is interesting that there is no similar value for
.)
lists several values for . This leads us to believe that the situation is not simple:
Table 2 Several values for Type II(a) for  .
.
Our data also show that, for a fixed value of , with
, the base case does not hold for several ranges of values of
, with
. Our next theorem shows this to be indeed the case in general.
Theorem 2.4
For a fixed , let
be the largest integer that satisfies
. Then, for
, and for
the base case does not hold; that is,
.
Proof
Since the inequalities in the statement of the theorem are well-defined.
We show that the split of into
and
and that of
into
and
(correspondingly) gives both of the relevant products exceeding that of the base case.
First, suppose this is not so for the first product; that is, It follows that
which violates the upper bound on
in the hypothesis, and so the first inequality is satisfied.
Similarly, suppose that Then
which violates the lower bound on
.
Consequently, the base case does not hold for the given values of and
. ■
With the notation as in Theorem 2.4, when, for example, , we have
. Then, for
, we have
; for
, we get
; and for
, we have
. Our data show that, for
, these are the only values of
for which the base case does not hold. We have verified similar results for other values of
up to 250. This leads us to make the following conjecture.
Conjecture 1
For Type II(a) and for fixed , the base case holds except for the ranges of values of
given by Theorem 2.4.
This still leaves some open problems for not only Type II(a), but for others that follow:
Problem 1
For the pairs for which the base case is known not to hold, determine the value of
.
Problem 2
For the pairs for which the base case is known not to hold, determine the value of
.
We have some partial results, but they shed little light on the general problem.
2.2.2 Type II(b)
Having shown that the base case sometimes holds, we next show that in Type II(b), when , the base case never holds. To this end, we introduce further notation that will also be used later. Let
, where
is the quotient and
the remainder when
is divided by
(
). Note that
, and if
then
. We also let
denote the minimum of the two products that result when there is a shift of
from the base case in the partition of
; that is,
Theorem 2.5
If and
with
, then the base case does not hold; that is,
.
Proof
Let with
. We observe that the difference of the products of the pairs
and
is
. Thus,
for
and
for
. It is easily checked that in both cases this number is better than the base case. ■
In effect, what the proof of Theorem 2.5 establishes is that, for the values of and
under consideration,
. We next show that equality holds here in some cases.
Theorem 2.6
Let and
with
and
. If
, then
.
Proof
When , we have
. Suppose there exist positive
and
such that
and
. Adding, and simplifying, we get,
Further simplification gives
so that
. ■
We conjecture that this result can be extended to higher values of :
Conjecture 2
If ,
,
, and
, then
.
We have verified our conjecture for . Furthermore, if the conjecture is true, then it is sharp in that there are values of
for which the result does not hold. For example, if
and
(so
and
), then
, while
with
and
as optimal pairs. Of course this is still greater than the base case value of 624.
2.3 Type III
Here things are not even this straightforward. As the bold-faced values of for
and 12 in show, the base case does not always hold. We note that for
and
, there are two optimal pairs
and
.
Table 3 Some values for Type III with  even and
even and  odd.
odd.
However, we show below that for a given value of , the base case is optimal for all but a finite number of values of
.
Theorem 2.7
Let and
.
(a) If is odd and
, then
.
(b) If is even and
, then
.
Furthermore, both bounds are sharp.
Proof
We first show that if the base case does not hold (that is, if ), then
.
Let and
be the quotient and remainder when
is divided by
, so
, with
and
. Suppose there is such a pair
for which the base case in not optimal. Then there exist
such that
(5) and
(6)
It follows from (Equation5(5) ) that
and
, and from (Equation6
(6) ) that
and
. We next simplify and solve (Equation5
(5) Equation6
(6) ) for
to get
(7) Substituting
and simplifying, we have
(8)
The first inequality of (Equation8(8) ) implies that
(9) while the second yields
(10) From (Equation7
(7) ) it follows that
, which reduces to
(11) Consequently,
.
Now assume that is odd. It follows that the base case holds if
, that is, if
. But since
is odd, this inequality is equivalent to
, which establishes (a).
Next, let be an even number for which the base case does not hold, and suppose that
. Then, as before, (Equation5
(5) ) through (Equation11
(11) ) hold. From (Equation11
(11) ) it follows that
, so
. Furthermore, from (Equation8
(8) ) it follows that
, so that
.
The inequalities (Equation8(8) ) now become
(8′) The inequality on the left yields
, which, together with (Equation10
(10) ), implies that
. Since
is even, it follows from the bound on
that
. Now (Equation5
(5) ) implies that
, so that
, which contradicts our hypothesis on
and establishes (b).
We now show that the bounds on are sharp. First, let
be odd and let
. It can be easily checked that each of the products in the split with pairs
and
is equal to
. Hence
, so the base case does not hold.
Now, let be even and let
. Then
and
. Consider the split with pairs
and
. It is straightforward to show that the product of the first is
and that of the second is
. Hence, once again,
, and the base case does not hold. ■
For a given value of and the finite numbers of values of
that do not satisfy the bounds in Theorem 3.1, we have data that show that
either equals the base case or is a value that follows certain formulas. Our data lead us to the conjecture below. As a reminder, the notation and restrictions are as follows:
,
with
and
if
is odd and
if
is even;
and
are such that
with
and
.
Conjecture 3
| 1. | If | ||||
| 2. | If | ||||
We note that in the case of odd, of the
values of
, the base case is conjectured to hold for
values and not to hold for
. Similarly, for
even, there are
values of
covered by the conjecture, with the base case believed to hold for
values of
and not to hold for
.
2.4 Type IV
As we will show, one reason why this case is interesting is because exact values have been hard to come by. Some examples are shown in . Following the format of earlier cases, we begin by fixing and varying
, but then we see that there are times to do the opposite.
Table 4 Some values for Type IV with  odd and
odd and  even.
even.
In the next two results we show that the only time that the base case holds (that is, where ) is when
.
Theorem 2.8
.
Proof
Suppose that there exist and
for which the products
and
both exceed
. It follows from the first inequality that
Since the second fraction is positive and
must be an integer, it follows that
. On the other hand, the second implies that
and from this we deduce, again since the fraction is positive, that
. Therefore, there cannot exist such
and
. ■
Theorem 2.9
Let and
. If
, then the base case does not hold; that is,
.
Proof
All that needs to be done is to find one pair of numbers and
for which both of the products
and
exceed
. Taking both
and
to be 1 suffices. With these values, we have
since
. We also have
which completes the proof. ■
It turns out that equality does not hold in general. We look next at some small values of .
Theorem 2.10
Let and
with
. Then for
,
| (a) |
| ||||
| (b) | |||||
| (c) | |||||
Proof
(a) Let with
. Then the split with pairs
and
shows that
. Suppose that equality does not hold. Then there exist
and
for which
and
. It is easily shown that
must then be 1. It follows from the first inequality that
and from the second that
, a contradiction.
(b) Let with
. For
, the split with pairs
and
shows that
. Now suppose that equality does not hold. Then there exist
and
for which
and
. If
, then the second inequality gives
or
, a contradiction. Hence
. It follows from the first inequality that
and from the second that
, another contradiction. Hence, equality for
holds. For
, we use the split with pairs
and
, and then the rest of the proof follows as before.
(c) The proof is similar to those of (a) and (b), and is therefore omitted. ■
We now go back to the other extreme, where is close to (but less than)
.
Theorem 2.11
Let , and let
and
. Further, let
and
. If
, then
.
Proof
It is easily seen that for ,
. Now assume that there exist
and
which give a better split of
and
, whence
and
. Then algebra yields
Since
or
, it follows that both fractions are positive, which yields
and
. This contradiction completes the proof. ■
We look next at values of close to about
. Our data indicate that here
.
Theorem 2.12
Let ,
and
. If
, then
except that
, and
.
Proof
Note that when ,
. Therefore, we assume that there exist
and
which give a better split of
and
; that is,
and
. Simplifying these, we get (a)
and (b)
. From (a) we deduce that since
,
, and hence
. From (b) we get
, and so
also. Moreover, from a combination of (a) and (b) we deduce that
, from which it follows that
since
by hypothesis.
Next let , and let
. It follows that
, or 6, and (a) and (b) reduce to
, so that
. Therefore there are just six possible pairs (r, s), and the values of
for these pairs follow by direct calculation. ■
We observe that not only does the conjecture of Gutiérrez and Lladó [Citation6] not hold, but there are values of and
for which it is off by an arbitrarily large amount. In fact, we have the following result that shows that
can exceed the base case by nearly
.
Theorem 2.13
Let and
. If
(that is,
), then
.
Proof
The split and
clearly gives the two equal products of
.
Suppose this is not optimal. Then there exist non-negative integers and
such that
It follows that
Simplification leads to , which is a contradiction, thus proving the theorem. ■
3 Summary
The main question considered in this paper is this: for two positive integers and
, maximize the minimum of the two numbers
and
over all integers
and
for which
and
. That is, determine
The problem is divided into four cases, depending on the parities of and
, with
: Types I and II: Both have the same parity; and Types III and IV: One is even and the other is odd. In each case, there is a natural lower bound, resulting from splitting
and
into two nearly equal parts. This is called the base case, and sometimes, even when the exact value of
has not been found, we are able to show that it exceeds the base case.
Type I: and
, and the base case is the pair
with value
.
Here, the base case always holds: .
Type II: and
with
, and the base case is the pair
with value
.
(a) . The base case holds for all
and
. Most of the other cases remain undetermined except for values found by computer.
(b) . The base case never holds. The exact value is known in some instances.
Type III: and
, the base case is again the pair
with value
.
The base case holds if is odd and
or if
is even and
, and these bounds are sharp.
Type IV: and
, the base case is again the pair
with value
.
The base case holds only when .
As to the question of which pairs and
does the base case hold, we have the following results for the four possible kinds of pairs.
Let and
be positive integers with
.
| • | If | ||||
| • | If | ||||
| • | If | ||||
| • | If | ||||
Thus, for any fixed , the answer to the base case question is known for all but finitely many values of
. In loose terms, we can say that the base case holds about half the time, depending on the parity of the smaller of the two numbers.
Since we began the paper with a discussion of line graphs and the line completion number of a graph, it seems appropriate to conclude with the following theorem on the line completion number of complete bipartite graphs, focusing on what eventually happens when the size of the smaller partite set is fixed. (Recall that .)
Theorem 3.1
The line completion number of the complete
-by-
bipartite graph with
fixed and
satisfies the following:
| (a) | For
| ||||||||||||||||
| (b) | For
| ||||||||||||||||
Notes
Peer review under responsibility of Kalasalingam University.
References
- K.S.BaggaL.W.BeinekeB.N.VarmaSuper line graphsY.AlaviA.SchwenkGraph Theory, Combinatorics, and Applications: Proceedings of the Seventh Quadrennial International Conference on the Theory and Applications of Graphs, vol. 11995Wiley3546
- J.S.BaggaL.W.BeinekeB.N.VarmaThe super line graph Discrete Math.20619995161
- J.S.BaggaL.W.BeinekeB.N.VarmaIndependence and cycles in super line graphsAustralas. J. Combin.191999171178
- X.LiH.LiH.ZhangPath-comprehensive and vertex-pancyclic properties of super line graph Discrete Math.308200863086315
- K.S.BaggaL.W.BeinekeB.N.VarmaThe line completion number of a graphY.AlaviA.SchwenkGraph Theory, Combinatorics, and Applications: Proceedings of the Seventh Quadrennial International Conference on the Theory and Applications of Graphs, vol. 21995Wiley11971201
- A.GutiérrezA.S.LladóOn the edge-residual number and the line completion number of a graphArs Combin.6320026574