Further results on super graceful labeling of graphs

Peer review under responsibility of Kalasalingam University.

Abstract

Let be a simple, finite and undirected graph of order and size . A bijection such that for every edge is said to be a -super graceful labeling of . We say is -super graceful if it admits a -super graceful labeling. For , the function is called a super graceful labeling and a graph is super graceful if it admits a super graceful labeling. In this paper, we study the super gracefulness of complete graph, the disjoint union of certain star graphs, the complete tripartite graphs , and certain families of trees. We also present four methods of constructing new super graceful graphs. In particular, all trees of order at most 7 are super graceful. We conjecture that all trees are super graceful.

Keywords:

• Graceful labeling
• Super graceful labeling
• Tree

1 Introduction

Let be a simple, finite and undirected graph of order and size . All notations not defined in this paper can be found in [1]. An injective function is called a graceful labeling of if all the edge labels of given by for every are distinct. This concept was first introduced by Rosa in 1967 [2]. Since then, there have been more than 1500 research papers published on graph labelings (see the dynamic survey by Gallian [3]).

Fig. 2 Super graceful labeling of .

Fig. 3 Super graceful labeling of .

In [4], the authors defined a -sequentially additive labeling of a graph as a bijection from to such that for each edge , . A graph admitting a -sequentially additive labeling is called a -sequentially additive graph. If , then is called a simply sequentially additive graph or an SSA-graph. They conjectured that all trees are SSA-graphs. More results on -sequentially additive labeling can be found in [5,6].

Definition 1.1

A bijection is called a -super graceful labeling if for every edge in . For , the function is called a super graceful labeling. We say is super graceful if it admits a super graceful labeling.

This is a generalization of super graceful labeling defined in [7,8]. Among others, the authors proved that paths, cycles, complete bipartite graphs and several families of trees are super graceful. In this paper, we continue with the search for super graceful graphs. We study the super gracefulness of complete graph, the disjoint union of certain star graphs, the complete tripartite graphs , and certain families of trees. We also present four methods of constructing new super graceful graphs. In particular, all trees of order at most 7 are super graceful. We conjecture that all trees are super graceful. Note that we only give the vertex labels of all the given examples.

2 New super graceful graphs

In [4], the authors showed that the complete graph is an SSA-graph if and only if .

Theorem 2.1

The complete graph is super graceful if and only if .

Proof

It is easy to verify that the sufficiency holds. To prove the necessity, we show that is not super graceful for . Assume that admits a super graceful labeling. Let , which is the largest label. Thus, cannot be a difference of other labels, must be a vertex label.

Case (1). 1 is a vertex label. This means is an edge label and 2 is not a vertex label. Hence cannot be a difference of two vertex labels. So 1 and are vertex labels. Then the difference is an edge label. Note that . Since , 2 and are edge labels, cannot be an edge label. Thus, is a vertex label. This yields a contradiction since , and are vertex labels creating 2 as an edge label twice.

Case (2). 1 is an edge label. The only way to have as an edge label would be an edge joining the vertices labeled 1 and , which is impossible in this case. Thus is a vertex label. Hence the edge labeled by 1 is incident with the vertices labeled by and . It follows that cannot be a vertex label. Thus is an edge label. The edge labeled by must be incident with the vertices labeled by and 2. Since and 2 are vertex labels, an edge which is incident with vertices labeled by and 2 is labeled by . By means of this fact and together with and 2 that served as vertex labels, 3 and 4 must be edge labels, respectively. 1, 3, 4, and are edge labels implies that and cannot be edge labels.

Finally, the edge joining the vertices labeled and , and the edge joining the vertices labeled and both have label 1, a contradiction.  ■

Theorem 2.2

The complete tripartite graph is super graceful for .

Proof

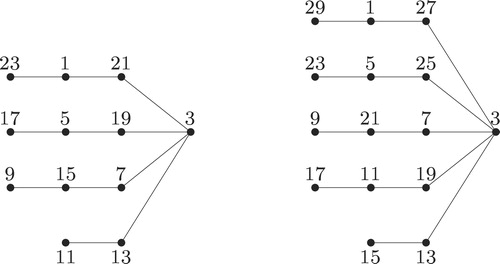
Let and . Now, and . Define a labeling as follows:

, for ; and

, for .

It is easy to verify that is a bijection with for every edge . Hence, is super graceful.  ■

Example 2.1

In Fig. 1, we give the super graceful labeling of according to the function defined above.

Fig. 1 Super graceful labeling of .

Problem 2.1

Study the super gracefulness of complete tripartite graph .

Definition 2.1

Let be the disjoint union of copies of star graphs for and .

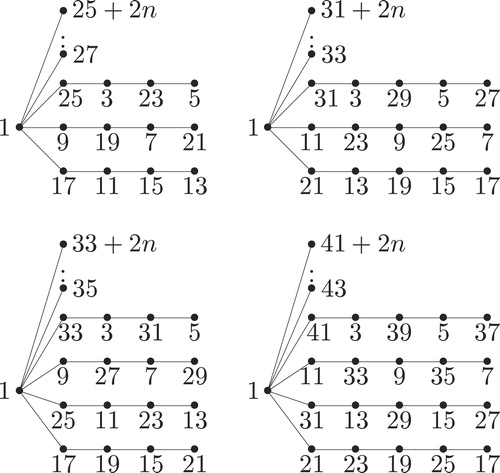
Theorem 2.3

The graph is super graceful if

(a)

.

(b)	for , the largest vertex label in is implies that .

Proof

Let with and . Clearly, and . Define a labeling as follows:

(a) Begin with the central vertex of each star subgraph .

(1)	Label the vertices by for .

(2)	For , label the edge and the vertex by and respectively for . Clearly, the set of used labels in is .

(3)	For , assume that the largest vertex label of is . Actually, . Define and , . Consider , where and . Then and . Hence the set of used labels for this subcase is . Combining all subcases, we can see that the set of used labels is .

(b) Begin with .

(1)	Label vertex by 1, edge by and vertex by for . Clearly, the set of used labels in is .

(2)	For , assume that the largest vertex label of is . Actually, . Define , and , . Observe that the set of used labels in is .

Thus, in both (a) and (b) above, is a bijection with for every edge in . Hence, is super graceful.  ■

Example 2.2

In Figs. 2 and 3, we give the super graceful labeling of (a) and (b) according to the function defined in (a) and (b) above, respectively.

3 Construction of super graceful graphs

In this section, we give four methods of constructing new super graceful graphs.

Construction C1. Let be a graph with a super graceful labeling having vertices that satisfy the following conditions:

(a)

;

(b)	is not a neighbor of .

By deleting the edge and adding a new edge , we obtained a new super graceful graph.

Example 3.1

Refer to the graph in Example 4.1. We let be the edge with label 8 such that and have labels 23 and 15 respectively. Let be the vertex with label 7. We can now delete edge and add a new edge with label 8. The obtained new graph is super graceful.

Construction C2. Let be a graph of order and size with a super graceful labeling . Let be a vertex of with .

(a)	Attached pendant edges to such that the newly added vertices are .

(b)	For , label vertex by and the corresponding pendant edge by .

Clear, the newly obtained graph is super graceful.

Example 3.2

We refer to the super graceful labeling of in Fig. 1 and add 4 pendant edges to the vertex with label 4. Label the newly added vertices by 23, 24, 25, 26 respectively and the corresponding pendant edges will have labels 19, 20, 21, 22. The new graph obtained is super graceful.

Construction C3. Let be a graph with a super graceful labeling .

(a)	Let and be two adjacent edges such that .

(b)	Suppose there exists a vertex such that .

(c)	Delete edges and and add edges and .

(d)	Label by and by .

It is clear that the new graph obtained is also super graceful.

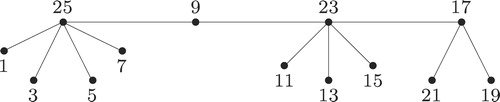
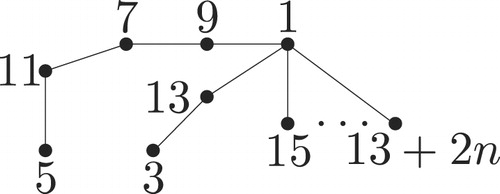
Example 3.3

Refer to the caterpillar in Example 4.1. We let be the vertices with labels respectively. Delete the edges and with labels respectively. Add 2 new edges and . Label and with . We have a new super graceful caterpillar.

Construction C4. Begin with vertices .

(a)	Label by for .

(b)	For , add a vertex and join it to each of .

(c)	Label edge by and vertex by .

(d)	Delete edge if its label is also one of the vertex labels.

(e)	For , introduce new vertices with labels , . Join each of them to . The induced edge labels are .

(f)	Delete each new edge in (e) if its label is one of the new vertex labels.

It is easy to verify that the bipartite graph we get now is super graceful.

Note: We can choose not to perform Steps (e) and (f). If we do perform Steps (e) and (f), the common new vertex labels and new edge labels introduced in part (e) are those of the new vertices except the last one. Thus edges with these labels are to be deleted.

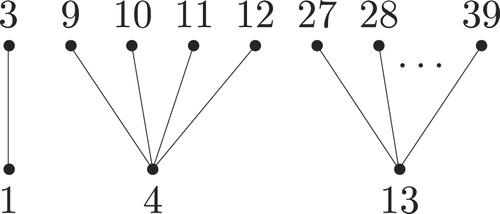
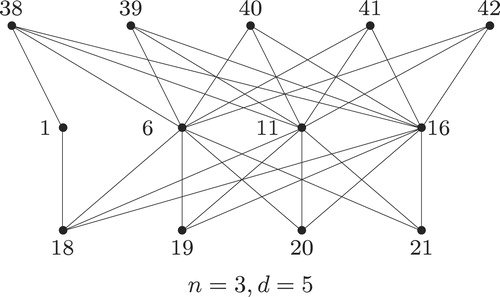
Example 3.4

In Fig. 4, we give an example for . In Step (a), vertices to are labeled respectively. In Steps (b) and (c), we add vertices to that are labeled 18 to 21 consecutively. In Step (d), we delete the edge joining vertices to . We then perform Steps (e) and (f) by taking . Thus, we add 5 more vertices that are labeled 38 to 42 consecutively.

Fig. 4 A super graceful graph under Construction C4.

Since this construction method will give us infinitely many connected super graceful bipartite graphs, we then have

Problem 3.1

Study the super gracefulness of connected bipartite graphs.

4 Super graceful trees

We now investigate the super gracefulness of some families of trees.

A caterpillar graph is a tree in which all the vertices are within distance 1 of a central path for . A caterpillar graph of order greater than 1 is a star graph when , which is for some . When , a caterpillar graph is obtained from a path by attaching pendant vertices () to each . We shall denote this caterpillar graph by . In [7,8], the authors showed that , and for are super graceful. We now show that is super graceful for , and , i.e., all caterpillar graphs are super graceful.

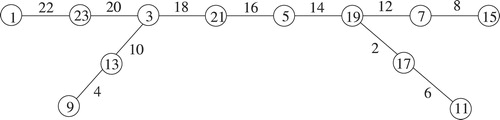
Theorem 4.1

The graph is super graceful for .

Proof

Define a labeling as follows:

for , and

for and .

For odd :

,

, ,

for ,

for , .

For even :

for ,

, for ,

for , .

It can be verified that is a bijection with for every edge . Hence, is super graceful. ■

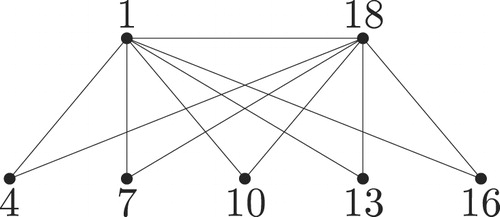
Example 4.1

In Fig. 5, we give the super graceful labeling of according to the function defined above.

Fig. 5 Super graceful labeling of .

Note that if or 2, we get that both the star graph and double star graph are super graceful.

Definition 4.1

Given paths of length with an end vertex . A spider graph is the one-point union of the paths at vertex .

In [7], the authors showed that , is super graceful. We now show that many other families of spider graphs are also super graceful. For simplicity, we shall use to denote a sequence of length in which all items are , where .

Theorem 4.2

The following spider graphs are super graceful.

(a)

, , ;

(b)

, ;

(c)

, ;

(d)

, ;

(e)

, , .

Proof

(a) Let and . Note that . Define a labeling as follows:

Case (1) is odd.

, for ,

for odd and even ,

for odd ,

for even and odd ,

for even .

Case (2) is even.

, for ,

for odd and even ,

for odd ,

for even and odd ,

for even .

It can be verified that is a bijection with all the vertex labels being odd and the edge labels being even such that for each edge , . Hence, is super graceful.

In Fig. 6, we give the super graceful labeling of , , , as defined above.

(b) Let and . Note that . Define a labeling as follows:

,

for odd , and for even ,

for odd , and for even .

It can be verified that is a bijection with all the vertex labels being odd and the edge labels being even such that for each edge , .

In Fig. 7, we give the super graceful labeling of and as defined above.

(c) Let and . Note is a super graceful path. For , we note that . Define a labeling as follows:

Case (1). is odd. We have

,

for even , for odd ,

for even , for odd ,

for even , for odd .

Case (2). is even. We have

,

for even , for odd ,

for even , for odd ,

for even , for odd .

It can be verified that is a bijection with all the vertex labels being odd and the edge labels being even such that for each edge , .

In Fig. 8, we give the super graceful labeling of and as defined above.

(d) We have . It is easy to verify that the labeling of the graph as shown in Fig. 9 is super graceful.

(e) We provide the proof for . In a similar way, it is easy to verify that the result holds for . We let and . Note that . Define a labeling as follows:

Case (1). is odd. We have

,

for odd , and for even .

Case (2). is even. We have

,

for odd , and for even .

We now let and . Note that . Define a labeling as follows:

Case (1). is odd. We have

,

for odd , and for even .

Case (2). is even. We have

,

for odd , and for even .

It can be verified that is a bijection with all the vertex labels being odd and the edge labels being even such that for each edge , . ■

Additionally, it is not difficult to see that is super graceful if we can prove the following:

Fig. 6 , , , are super graceful.

Fig. 7 and are super graceful.

Fig. 8 and are super graceful.

Fig. 9 is super graceful.

Problem 4.1

Let be any real number.

(1) Given the sequence , , we can always arrange the numbers as a sequence so that the difference of the pairs of consecutive numbers is even from 2 to .

(2) Given the sequence , , we can always arrange the numbers as a sequence so that the difference of the pairs of consecutive numbers is even from 2 to .

Note that the spider in Case (e) is also known as lobsters. Observe that we always label the end-vertex, , of the longest path with 1. If we identify the central vertex of a star , to , then the new graph is also super graceful by labeling the end-vertices of with for . Hence, we have obtained new families of super graceful lobsters.

Consider another lobster tree, , having a longest path and two subpaths and . For , we obtained that the tree is super graceful. The labelings of the vertices in the order of are given below:

.

The case is shown in Fig. 10.

Fig. 10 is super graceful.

Problem 4.2

Show that the lobster tree is super graceful for all .

Moreover, we may consider case (a) of Theorem 4.2 for . That means we may ignore all the vertices ’s. By using the same labeling and combining with Theorem 2.3 for the case , we get the result of Perumal et al. [7].

Corollary 4.3

The spider graphs are super graceful, where and .

Combining with Theorems 2.3, 4.1 and 4.2 and Corollary 4.3, we can conclude that all trees of order at most 7 are super graceful.

Note that the Construction C2 can be used repeatedly to any super graceful tree to create infinitely many super graceful trees. Hence, we end this paper with the following conjecture.

Conjecture 4.1

All trees are super graceful.

Notes

Peer review under responsibility of Kalasalingam University.