Abstract
Let be a digraph possibly with loops and
a finite digraph without loops whose arcs are colored with the vertices of
(
is an
-colored digraph). V(
) and A(
) will denote the sets of vertices and arcs of
respectively. For an arc (
) of
we will denote by
(
) its color. A directed walk (respectively directed path) (
,
) in
is an
-walk (respectively
-path) if and only if (
(
),
) is a directed walk in
. A set
is an
-kernel by walks (respectively
-kernel) if for every pair of different vertices in
there is no
-walk (respectively
-path) between them, and for every vertex
there exists
such that there exists an
-walk (respectively
-path) from
to
in
.
Let be an arc-colored digraph. The color-class digraph of
, denoted by
(
), is defined as follows: the vertices of the color-class digraph are the colors represented in the arcs of
and (
)
A(
(
)) if and only if there exist two arcs namely (
)
A(
) colored
and (
)
A(
) colored
. In this paper we relate the concepts discussed above, the color-class digraph and the
-coloration of
, in order to prove the existence of an
-kernel by walks (respectively
-kernel).
1 Introduction
For general concepts we refer the reader to [Citation1] and [Citation2]. A directed walk is a sequence () such that (
)
A(
) for each
. Moreover if
for
, then it is called directed path. A directed cycle is a directed walk (
,
) such that
for
,
. If
is an infinite digraph, an infinite outward path is an infinite sequence (
) of distinct vertices of
such that (
)
A(
) for each
. In this paper we are going to write walk, path, cycle instead of directed walk, directed path, directed cycle, respectively.
A digraph is said to be arc-colored if its arcs are colored. A digraph
is said to be
-colored if the arcs of
are colored with
colors. Let
be an arc-colored digraph. A path is called monochromatic if all of its arcs are colored alike. For an arc (
) of
we will denote by
(
) its color.
In [Citation3] Sands et al. proved that if the arcs of a finite tournament are colored with two colors, then there is always a single vertex reachable from any other by a monochromatic path. In [Citation4] Linek and Sands gave an extension of the result of Sands et al. in which the arcs of a tournament are colored with the elements of a partially ordered set
. They called a path (
) in
monotone if
in
for each
. In [Citation4] Linek and Sands considered a further extension as follows: if
is a reflexive digraph and
is a tournament whose arcs are colored by the vertices of
, an
-path
in
is a path in
for which
for any two consecutive arcs (
) and (
) in
.
In [Citation5] Arpin and Linek reconsidered the last extension suggested in [Citation4] in order to assign a color to the arcs of a multidigraph with the vertices of a digraph
(possibly irreflexive). They called a walk or a path (
,
) in
an
-walk or an
-path, respectively, iff (
(
),
(
)) is a walk in
. Notice that an arc is an
-path, that is to say, a singleton vertex is a walk in
. They also called a set of vertices
-absorbent by walks if for every
there is an
-walk from
to some point of
and a set
was called
-independent by walks if there is no
-walk between any two distinct vertices of
. Since the existence of an
-walk between two vertices does not guarantee the existence of an
-path between those vertices (although for some
this is true) and the concatenation of two
-paths is not always an
-path, in [Citation5] Arpin and Linek prefer to work with
-walks instead of
-paths. In [Citation5] they classify
(the class of all
such that any multidigraph
arc-colored with the vertices of
has an independent set of vertices that is
-absorbent by walks) and they make inroads in the classification of
(the class of all
such that any multidigraph
arc-colored with the vertices of
has a set of vertices
that is both
-independent by walks and
-absorbent by walks) and
(the class of all
such that any tournament arc-colored with the vertices of
has a single vertex
-absorbent by walks).
In [Citation6] Galeana-Sánchez and Delgado-Escalante used the work of Arpin and Linek [Citation5] in order to introduce the following concepts:
Definition 1.1
A subset of V(
) is said to be an
-kernel by walks if it satisfies the following two conditions:
| 1. | For every pair of different vertices in | ||||
| 2. | For every vertex | ||||
Definition 1.2
A subset of V(
) is said to be an
-kernel if it satisfies the following two conditions:
| 1. | For every pair of different vertices in | ||||
| 2. | For every vertex | ||||
Since the existence of an -walk between two vertices does not guarantee the existence of an
-path between those vertices and the concatenation of two
-paths is not always an
-path, we can claim that if
has an
-kernel by walks, then
not necessarily has an
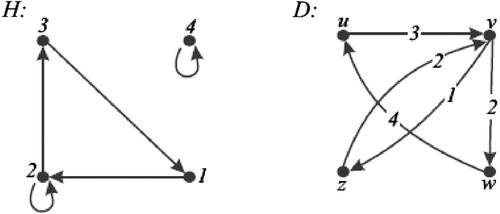
-kernel as the example in shows. In we have that
is an
-kernel by walks of
, because (
,
,
,
,
) is an
-walk in
that finishes in
and it contains every vertex of
. It is easy to check that
has no
-kernel (notice that every
-independent set of
has cardinality one).
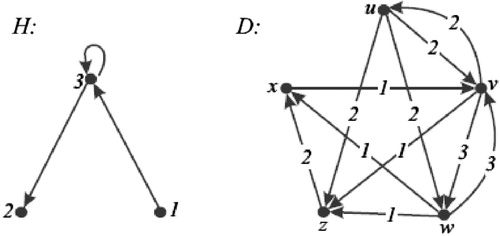
We also claim that if has an
-kernel, then
not necessarily has an
-kernel by walks as the example in shows. In we have that
is an
-kernel in
. It is easy to see that
has no
-kernel by walks (notice that every
-independent set by walks in
has cardinality one because (
,
,
,
,
) is an
-walk between
and
in
).
In [Citation6] Galeana-Sánchez and Delgado-Escalante proved the existence of -kernels in possibly infinite
-colored digraphs. In [Citation7] Galeana-Sánchez and Sánchez-López showed necessary and sufficient conditions for the existence of
-kernels in the
-join of digraphs. Finally in [Citation8] Galeana-Sánchez and Sánchez-López showed more conditions for the existence of
-kernels in infinite digraphs.
1.1 Kernels and kernels by monochromatic paths
A subset of V(
) is said to be a kernel if it is both independent (a vertex in
has no successor in
) and absorbing (a vertex not in
has a successor in
). This concept was first introduced in [Citation9] by von Neumann and Morgenstern in the context of Game Theory as a solution for cooperative
-player games. If every induced subdigraph of
has a kernel,
is said to be a kernel perfect digraph. The concept of kernel is important to the theory of digraphs because it arises naturally in applications such as Nim-type games, logic, and facility location, to name a few. Several authors have investigated sufficient conditions for the existence of kernels in digraphs. For comprehensive surveys see, for example, [Citation10] and [Citation11].
Let be an arc-colored digraph. A subset
of V(
) is said to be a kernel by monochromatic paths if it satisfies the following two conditions: (1) No two vertices of
are connected by a monochromatic path (
is independent by monochromatic paths) and (2) For every vertex
of V(
) not in
there is a monochromatic path from
to a vertex in
(
is absorbent by monochromatic paths).
The concept of kernel by monochromatic paths generalizes that of kernel, since a digraph has a kernel if and only if the
-colored digraph
, in which every two different arcs have different colors, has a kernel by monochromatic paths. And the concept of
-kernel is also indeed a generalization of the concept of kernel by monochromatic paths when A(
) consists only of loops.
In 1982, Sands et al. [Citation3] proved the following.
Theorem 1.3
Sands, Sauer and Woodrow [Citation3]
Every 2-colored multidigraph without monochromatic infinite outward path has a kernel by monochromatic paths.
Due to the difficulty that it represents to find kernels by monochromatic paths in arc-colored digraphs, sufficient conditions for the existence of kernels by monochromatic paths in arc-colored digraphs have been obtained mainly by adding a condition on the monochromaticity or quasi-monochromaticity of small subdigraphs like cycles, paths, small sized subtournaments, vertex neighborhoods, and so on, see for example [Citation12–Citation[13]Citation14,Citation3].
Let be an arc-colored digraph. The color-class digraph of
, denoted by
(
), is the digraph defined as follows: the vertices of the color-class digraph are the colors represented in the arcs of
and (
)
A(
(
)) iff there exist two arcs namely
colored
and (
)
A(
) colored
.
In [Citation15] Galeana-Sánchez introduced the concept of color-class digraph of mainly to prove that if
is a finite arc-colored digraph such that
(
) is a bipartite digraph, then
has a kernel by monochromatic paths. With this result she obtained a generalization of the result given by Sands et al. [Citation3] when
is finite and strong.
Since V((
))
V(
), our main question is: What structural properties of
(
), with respect to
, imply that
has either an
-kernel by walks or an
-kernel?
Let be a partition of V(
(
)) and
. An
-walk
of
will be called a
-colored
-walk if
for every (
)
A(
), for some fixed
.
In [Citation8] Galeana-Sánchez and Sánchez-López proved for infinite digraphs the following:
Theorem 1.4
[Citation8]
Let be a digraph,
an
-colored digraph (possibly infinite) and
(
) the color-class digraph of
. Suppose that there exists a partition
of V(
(
)) such that:
| 1. |
| ||||
| 2. | if ( | ||||
| 3. |
| ||||
In order to prove Theorem 1.4 they applied Theorem 1.3 to another 2-coloring of the arcs of which was defined quite naturally from the partition given in the conditions of Theorem 1.4.
In this paper we are going to activate the idea of the proof of Theorem 1.4 in order to prove the following theorem.
Theorem 1.5
Let be a digraph,
an
-colored digraph and
(
) the color-class digraph of
. Suppose there exist
, with
, and
a partition of V(
(
)) such that:
| 1. |
| ||||||||||||||||
| 2. | For | ||||||||||||||||
In [Citation5] Arpin and Linek defined what is the reachability digraph of an -colored digraph
, denoted by
(
), as follows:
and
.
We will also prove the following:
Theorem 1.6
Let be a digraph,
an
-colored digraph and
(
) the color-class digraph of
. If there exists a partition
of V(
(
)) such that:
| (1) | There are no | ||||
| (2) | If ( | ||||
| (3) | Let | ||||
| (4) | Let | ||||
2 Preliminaries
An arc of the form () is a loop.
is a looped digraph if and only if (
)
A(
) for all
. For
the subdigraph of
induced by
, denoted by
[
], has
and
. In a digraph (possibly with loops) we shall say that a subset
of V(
) is independent if the only arcs in
[
] are loops. For
and
two subsets of V(
) an arc (
)
A(
) is called an
-arc whenever
and
. For
a
-walk(path) is a walk(path) from
to
in
. Let
be a walk, if
then the
-walk(path) contained in
will be denoted by (
,
,
). If
and
then a walk(path) from
to
, denoted by
-walk(path), is a
-walk(path) for some
. If
and
are two subsets of V(
) then a walk(path) from the set
to the set
, denoted by
-walk(path), is a
-walk(path) for some
and for some
. A digraph
is a bipartite digraph if there is a partition
of V(
) such that
[
] is an independent set for each
.
For the rest of the work is a digraph possibly with loops and
is a finite digraph without loops.
3 Main results
The following lemma, which was proved in [Citation5], will be useful in order to prove Theorems 1.5 and 1.6.
Lemma 3.1
If , then
for each
.
Theorem 3.2
Let be a digraph,
an
-colored digraph and
(
) the color-class digraph of
. Suppose there exist
, with
, and
a partition of V(
(
)) such that:
| (1) |
| ||||||||||||||||
| (2) | For | ||||||||||||||||
Proof
Let be a digraph,
an
-colored digraph and
as in the hypothesis of Theorem 3.2.
In order to prove that has an
-kernel by walks, consider the
-colored digraph
obtained from
as follows:
The following claim will be useful in order to prove Theorem 3.2.
Claim 1. There exists a -
-walk in
if and only if there exists a
-
-walk in
.
(necessity) Let be a
-
-walk in
. Suppose that
for each
. Since (
) is a walk in
(by construction of
), it remains to prove that
for each
.
Let .
If , then
. So (
(
) =
(
) =
)
A(
), because
.
Suppose that . From the definition of
-walk and the definition of
(
) we get that
. So from condition (2) of Theorem 3.2 we get that every
-arc in
(
) is an arc of
for each
. Then, it follows from condition (1) of Theorem 3.2 that
.
Therefore (,
) is a
-
-walk in
.
(sufficiency) Let be a
-
-walk in
. Suppose that
(
) =
for each
. Then, from the construction of
we have that
for each
.
Since (,
) is a walk in
(by construction of
), it remains to prove that
A(
) for each
.
Let .
If , then (
(
),
(
))
A(
) (
,
and
).
Suppose that . Since (
)
A(
) (because
is an
-walk in
), from condition (1) of Theorem 3.2 we get that every
-arc in
(
) is an arc of
. On the other hand, since
,
and
, it follows that
.
Therefore (,
) is a
-
-walk in
.
Since is an
-colored digraph and
, it follows that
has an
-kernel by walks, say
. So by Claim 1 we get that
is an
-kernel by walks in
. ■
Note 3.1
Theorem 3.3 shows that if in Theorem 3.2 is a transitive digraph then the
-kernel by walks
is an
-kernel.
Theorem 3.3
[Citation7]
Let H be a transitive digraph and an
-colored digraph.
V(
) is an
-kernel by walks in
if and only if
is an
-kernel in
.
Theorem 3.2 allows us to establish the following results. Before we need a definition.
Let be a digraph with
,
, and
a sequence of vertex disjoint digraphs with
and
for each
. The
-join of the digraph
and the sequence
is the digraph
(
) such that:
Notice that from the definition of (
) we have that
(
) contains an isomorphic digraph to
for each
. Denote by
the copy of
in
(
).
Observe that .
The following theorem shows how to produce more digraphs in from a digraph in
. It is necessary to mention that the following result was proved in [Citation5] by Arpin and Linek. Here we are going to prove that Theorem 3.4 is also a direct consequence of Theorem 3.2.
Theorem 3.4
Let , with
,
, and
a sequence of vertex disjoint complete digraphs. Then
.
Proof
Let be a
(
)-colored digraph.
We are going to prove that has a
(
)-kernel by walks.
Claim 1. is a looped complete digraph for each
.
Let . Since
is a complete digraph and
, from the definition of
(
) we have that
is a looped complete digraph.
Let for each
.
Consider the partition of V(
(
)).
The following claims on the partition will be useful in order to prove Theorem 3.4.
Let .
Claim 2. For , suppose that there exists a
-arc in
(
). Then (
)
A(
) if and only if every
-arc in
(
) is an arc of
(
).
(necessity) Since ()
A(
), from the definition of
(
) we get that ((
),(
))
A(
(
)) for each (
)
V(
) and for each (
)
V(
). Thus if there exists a
-arc in
(
), say
, it holds that
(because
and
).
(sufficiency) Since there exists a -arc in
(
), say (
), it follows from hypothesis of Claim 2 that
. On the other hand, since
, it follows from the definition of
(
) that
(recall
).
Claim 3. .
Since is a looped complete digraph (Claim 1) for each
and
(because
), it follows that
(
)[
] is a looped complete digraph. So
for each
.
Claim 4. For , if there exists a
-arc in
, then every
-arc in
(
) is an arc of
(
).
Suppose that there exists a -arc in
, say (
).
Since , from the definition of
(
) we have that
for each
and for each
. So if there exists a
-arc in
(
), say
, it holds that
(because
and
).
Hence, it follows from Theorem 3.2 that has a
(
)-kernel by walks. So
. ■
Theorem 3.5
Let be a looped digraph,
an
-colored digraph and
(
) the color-class digraph of
. Suppose there exists a partition
of V(
(
)) such that:
| 1. |
| ||||
| 2. |
| ||||
| 3. | There are no arcs between ( | ||||
Proof
Let be the digraph with vertices
and arcs
.
In order to prove Theorem 3.5, consider the following claims.
Claim 1. For , suppose there exists a
-arc in
(
). Then (
)
A(
) if and only if every
-arc in
(
) is an arc of
.
(necessity) From condition (2) of Theorem 3.5 we have that every -arc in
(
) is an arc of
for each
. So it holds that if (
)
A(
) then every
-arc in
(
) is an arc of
for each
.
(sufficiency) Since there exists a -arc in
(
) and there are no arcs between (
) and
in
(by condition (3) of Theorem 3.5), it follows that
.
If and
, it holds that if every
-arc in
(
) is an arc of
, then (1,2)
A(
) (recall that (1,2)
A(
)). On the other hand, if
and
, it holds that if every
-arc in
(
) is an arc of
, then (2,1)
A(
) (recall that (2,1)
A(
)).
Claim 2. .
Since is an independent set in
(
) and
[
] is a looped digraph for each
(because
is a looped digraph), it follows that
.
Claim 3. For , if there exists a
-arc in
, then every
-arc in
(
) is an arc of
.
Since there are no arcs between () and
in
, it follows that
.
If and
, let
be a
-arc in
. Since
for each
and for each
(condition (2) of Theorem 3.5), we have that
.
If and
, let
be a
-arc in
. Since
for each
and for each
(condition (2) of Theorem 3.5), we have that
.
Therefore, from Theorem 3.2 we have that has an
-kernel by walks, which is an
-kernel by Note 3.1. ■
Theorem 3.6
Let be a looped digraph,
an
-colored digraph and
(
) the color-class digraph of
. Suppose there exists an independent set
in V(
(
)) such that:
| (1) |
| ||||
| (2) |
| ||||
| (3) | There are no arcs between | ||||
Proof
Let be the digraph with vertices
and arcs
.
Let be a partition of V(
(
)).
In order to prove Theorem 3.6, consider the following claims.
Claim 1. For , suppose there exists a
-arc in
(
). Then
if and only if every
-arc in
(
) is an arc of
.
(necessity) If and
, suppose there exists a
-arc in
(
), say
, such that
. We are going to see that
. Since
, we have that
.
If and
, suppose there exists a
-arc in
(
), say
, such that
. We are going to see that
. Since
, we have that
.
(sufficiency) If and
, suppose that
. We are going to see that there exists a
-arc in
(
), say
, such that
. From the hypothesis of Claim 1, it follows that there exists a
-arc in
(
), say
. On the other hand, from condition (3) of Theorem 3.6 we have that
.
If and
, suppose that
. We are going to see that there exists a
-arc in
(
), say
, such that
A(
). From the hypothesis of Claim 1, it follows that there exists a
-arc in
(
), say
. On the other hand, from condition (3) of Theorem 3.6 we have that
.
Claim 2. .
Since is an independent set in
(
) and
[
] is a looped digraph, then
. On the other hand, since
[
] is a looped complete digraph in
, it holds that
.
Claim 3. For , if there exists a
-arc in
, then every
-arc in
(
) is an arc of
.
If and
, suppose there exists a
-arc in
(
), say
, such that
. We are going to see that there are no
-arcs in
.
From condition (3) of Theorem 3.6 we have that there are no -arcs in
. So there are no
-arcs in
.
If and
, suppose there exists a
-arc in
(
), say
, such that
. We are going to see that there are no
-arcs in
.
From condition (3) of Theorem 3.6 we have that there are no -arcs in
. So there are no
-arcs in
.
Therefore, it follows from Theorem 3.2 that has an
-kernel by walks, which is an
-kernel by Note 3.1. ■
The following result shows another sufficient condition for the existence of an -kernel by walks.
Theorem 3.7
Let be a digraph,
an
-colored digraph and
(
) the color-class digraph of
. If there exists a partition
of V(
(
)) such that:
| (1) | There are no | ||||
| (2) | If ( | ||||
| (3) | Let | ||||
| (4) | Let | ||||
Proof
We will use the following notation.
Let V(
) and
. We will write:
if there exists a
-colored
-walk from
to
in
;
if there exists a
-colored
-walk from
to
in
;
if there exists a
-colored
-walk from
to
in
;
is the denial of
, and so on. In the same way we define
if there exists an
-walk from
to
in
, and so on.
Consider the following claims.
Claim 1. Every -walk in
is either a
-colored
-walk or a
-colored
-walk.
Proceeding by contradiction, suppose that there exists an -walk in
, say
, which is neither
-colored nor
-colored. Then there exist two consecutive arcs (
) and (
) in
for some
such that either (
and
) or (
and
). Since
(by definition of
(
)) and there are no
-arcs in
(
) we get that
and
. On the other hand, since
is an
-walk in
we have that
, contradicting condition (2) of Theorem 3.7.
On the other hand, let be an
-kernel by walks of
. If
is an
-independent set by walks in
, then
is an
-kernel by walks of
(recall that V(
) = V(
)). Therefore suppose that
is not an
-independent set by walks in
.
Claim 2. If for some
and for some
, with
, then
.
Since is an
-independent set by walks in
, from both the construction of
and Claim 1 it follows that
.
Claim 3. If , with
and
, then
for each
.
Proceeding by contradiction, suppose that there exist , with
, and
such that
and
.
Since , it follows that there exists
such that
. On the other hand, since
, we have that there exists
such that
. Therefore from the definition of color-class digraph we get that
. So, there exists a
-arc in
(
), contradicting condition (1) of Theorem 3.7.
Claim 4. .
Since , it follows from the construction of
that V(
) is not an
-independent set by walks in
. So,
.
Let .
Notice that , because
is not an
-independent set by walks in
.
Let .
Claim 5. .
Proceeding by contradiction, suppose that . Since
(by Claim 4) and
is an
-kernel by walks of
, it follows that there exist
and
such that
. On the other hand, since
, it follows from the definition of
that for
there exists
such that
, contradicting Claim 3.
Claim 6. is an
-independent set by walks in
.
Since and
is an
-independent set by walks in
, it follows from the construction of
that
for each
, with
. On the other hand, from the definition of
we have that
for each
, with
.
Therefore is an
-independent set by walks in
.
Claim 7. For each there exists
such that
.
Let . Since
is an
-kernel by walks of
, it follows that there exists
such that
. On the other hand, from both Claim 3 and the definition of
we have that
. So
.
If for each
, then it follows from Claims 6 and 7 that
is an
-kernel by walks of
(recall that V(
) = V(
)). Therefore suppose that there exists
such that
.
Let .
Since (
) is a kernel perfect digraph, we have that
(
)[
] (the subdigraph of
(
) induced by the set
) contains a kernel, say
.
Claim 8. is an
-independent set by walks in
.
Proceeding by contradiction, suppose that is not an
-independent set by walks in
. Then there exist
and
in
, with
, such that
. Since
and
is an
-kernel by walks of
, it follows that
, which implies that there exists an
-walk from
to
in
(by the definition of
). So from the definition of reachability digraph we get that (
)
A(
(
)). Therefore
, which contradicts that
is an
-independent set in
(
)[
].
Claim 9. For each there exists
such that
.
Let . Since
and
is a kernel of
(
)[
], it follows that there exists
such that
. Since
(
), we have that (
)
A(
(
)). So from the definition of reachability digraph we have that there exists an
-walk from
to
in
. Therefore there exists an
-walk from
to
in
(because
is a subdigraph of
).
Claim 10. is an
-kernel by walks of
.
(a) is an
-independent set by walks in
.
Since and
are
-independent sets in
(by Claims 6 and 8, respectively), it remains to prove that there exist no
-
-walks in
and there exist no
-
-walks in
.
Since , from the definition of
we have that there exist no
-colored
-
-walks in
. Since
is an
-independent set by walks in
, we get that there exist no
-colored
-
-walks in
. On the other hand from the definition of
there exist no
-
-walks in
(because
).
Therefore, is an
-independent set by walks in
.
(b) is an
-absorbent set by walks in
.
It follows from Claims 7 and 9 and the definition of .
Therefore has an
-kernel by walks. ■
Note 3.2
The example of shows that there exist -colored digraphs which holds the hypotheses of Theorem 3.2 and it does not hold the hypotheses of Theorem 3.7.
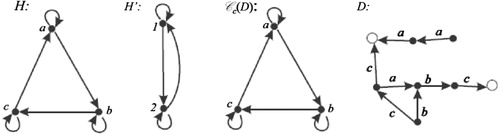
Note 3.3
The example of shows that there exist -colored digraphs which hold the hypotheses of Theorem 3.7 and it does not hold the hypotheses of Theorem 3.2.
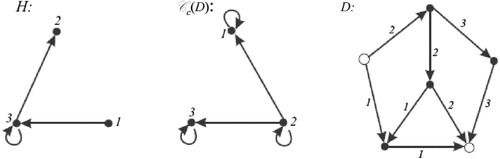
Notes
Peer review under responsibility of Kalasalingam University.
References
- J.Bang-JensenG.GutinDigraphs: Theory, Algorithms and Applications2000Springer-VerlagLondon
- C.BergeGraphs1989North-HollandAmsterdan
- B.SandsN.SauerR.WoodrowOn monochromatic paths in edge colored digraphsJ. Combin. Theory Ser. B331982271275
- V.LinekB.SandsA note on paths in edge-colored tournamentsArs Combin.441996225228
- P.ArpinV.LinekReachability problems in edge-colored digraphsDiscrete Math.307200722762289
- P.Delgado-EscalanteH.Galeana-SánchezRestricted domination in arc-colored digraphsAKCE Int. J. Comb.1201495104
- H.Galeana-SánchezR.Sánchez-LópezH-kernels in the D-joinArs Combin.982011353377
- H.Galeana-SánchezR.Sánchez-LópezH-kernels in infinite digraphsGraphs Combin.292013913920
- J.V.NeumannO.MorgensternTheory of Games and Economic Behavior1944Princeton University PressPrinceton, NJ
- E.BorosV.GurvichPerfect Graphs, Kernels and Cores of Cooperative Games, RUTCOR Research Report 122003Rutgers University April
- A.S.FraenkelCombinatorial games: Selected bibliography with a succinct gourmet introductionElectron. J. Combin.14Dynamic Survey DS22009http://www.combinatorics.org/ojs/index.php/eljc/article/view/DS2/pdf
- H.Galeana-SánchezOn monochromatic paths and monochromatic cycles in edge colored tournamentsDiscrete Math.1561996103112
- H.Galeana-SánchezKernels in edge colored digraphsDiscrete Math.18419988799
- S.MinggangOn monochromatic paths in m-colored tournamentsJ. Combin. Theory Ser. B451988108111
- H.Galeana-SánchezKernels by monochromatic paths and the color-class digraphDiscuss. Math. Graph Theory312011273281