Crosscap of the non-cyclic graph of groups

Peer review under responsibility of Kalasalingam University.

Abstract

The non-cyclic graph to a non locally cyclic group is as follows: take as vertex set, where is called the cyclicizer of , and join two vertices if they do not generate a cyclic subgroup. In this paper, we classify the finite groups whose non-cyclic graphs are outerplanar. Also all finite groups whose non-cyclic graphs can be embedded on the torus or projective plane are classified.

Keywords:

• Non-cyclic group
• Non-cyclic graph
• Planar graph
• Genus
• Crosscap

1 Introduction

In order to get a better understanding of a given algebraic structure , one can associate to it a graph and study an interplay of algebraic properties of and combinatorial properties of . In particular there are many ways to associate a graph to a group. For example commuting graph of groups, non-commuting graph of groups, non-cyclic graph of groups and generating graph of group have attracted many researchers towards this dimension. One can refer [1–6^{[1][2][3][4][5][6]}] for such studies.

Fig. 1a .

Fig. 1b Embedding of in .

Fig. 2a .

Fig. 2b .

Let be a non locally cyclic group. In [1], Abdollahi and Hassanabadi introduced the graph of defined as follows: take as vertex set, where is called the cyclicizer of , and join two vertices if they do not generate a cyclic subgroup. Especially, the embeddings of non-cyclic graph help us to explore some interesting results related to algebraic structures of groups. In this paper, we try to classify all finite groups whose non-cyclic graphs are outerplanar and it can be embedded on the torus or projective plane.

By a graph , we mean an undirected simple graph with vertex set and edge set . A graph in which each pair of distinct vertices is joined by the edge is called a complete graph. We use to denote the complete graph with vertices. An -partite graph is one whose vertex set can be partitioned into subsets so that no edge has both ends in any one subset. A complete -partite graph is one in which each vertex is joined to every vertex that is not in the same subset. The complete bipartite graph (2-partite graph) with part sizes and is denoted by . A graph is said to be planar if it can be drawn in the plane so that its edges intersect only at their ends. A subdivision of a graph is a graph obtained from it by replacing edges with pairwise internally-disjoint paths. A remarkably simple characterization of planar graphs was given by Kuratowski in 1930. Kuratowski’s Theorem says that a graph is planar if and only if it contains no subdivision of or (see [7, p. 153]).

By a surface, we mean a connected two-dimensional real manifold, i.e., a connected topological space such that each point has a neighborhood homeomorphic to an open disk. It is well known that any compact surface is either homeomorphic to a sphere, or to a connected sum of tori, or to a connected sum of projective planes (see [8, Theorem 5.1]). We denote for the surface formed by a connected sum of tori, and for the one formed by a connected sum of projective planes. The number is called the genus of the surface and is called the crosscap of . When considering the orientability, the surfaces and sphere are among the orientable class and the surfaces are among the non-orientable one. In this paper, we mainly focus on the non-orientable cases.

A simple graph which can be embedded in but not in is called a graph of genus . Similarly, if it can be embedded in but not in , then we call it a graph of crosscap . The notations and are denoted for the genus and crosscap of a graph , respectively. It is easy to see that and for all subgraphs of . For details on the notion of embedding of graphs in surface, one can refer to A.T. White [9].

The following results are useful in the following subsequent section.

Theorem 1.1

[10]

For positive integers and , we have the following:

(i) if ;

(ii) if .

Theorem 1.2

[10]

Let be integers and for a real number is the least integer that is greater than or equal to . Then

(i)

(ii) , where .

Theorem 1.3

[10]

Let be a simple graph with vertices and edges. Then .

Theorem 1.4

[10]

Let be a connected graph with vertices and edges. Then .

2 Crosscap of non-cyclic graph

In this paper, we try to classify all finite groups whose non-cyclic graphs are outerplanar and it can be embedded on the torus or projective plane. The following are useful in the sequel of this section and hence given below:

Theorem 2.1

[2]

Let be a group of size and exponent , where is a prime number and is an integer. Then .

Theorem 2.2

[2]

Let be a non locally cyclic group. Then is planar if and only if is isomorphic to .

An undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. There is a characterization for outerplanar graphs that says that a graph is outerplanar if and only if it does not contain a subdivision of or .

Theorem 2.3

Let be a finite non-cyclic group. Then is outerplanar if and only if .

Proof

Assume that is outerplanar. Then we have . Suppose . Since is connected, there exist such that is non-cyclic. Therefore make a subgraph, which is a contradiction. Suppose that contains an element such that . Then where is non-cyclic, make a subgraph isomorphic to , which is again a contradiction. Thus with exponent 2, where . By Theorem 2.1, and so . □

Theorem 2.4

Let be a finite non locally cyclic group. Then if and only if is isomorphic to one of the following groups: , , , , .

Proof

Assume that . Since and we have, . Using this, Since for all , we get, which implies that 2. Suppose that . Then the subgraph induced by is isomorphic to and so is a subgraph of . Hence and so and by Theorem 2.2, . Since is not cyclic, .

If , then by using Theorem 2.2, is isomorphic to , , or .

If , then is isomorphic to . If , then and so the vertex sets and make a subgraph, which is a contradiction.

If , then , or . Suppose . Since has 3 elements of order 2 and 8 elements of order 3, these elements make a subgraph of , which is a contradiction. If , then is a subgraph of and hence . If , then we can find a suitable set of vertices such that they make a subgraph, a contradiction. Hence .

If , then . Since is a subgraph of , . If , then is isomorphic to one of the following groups:

Then we can find a suitable set of vertices such that they make either or as a subgraph and so , a contradiction.

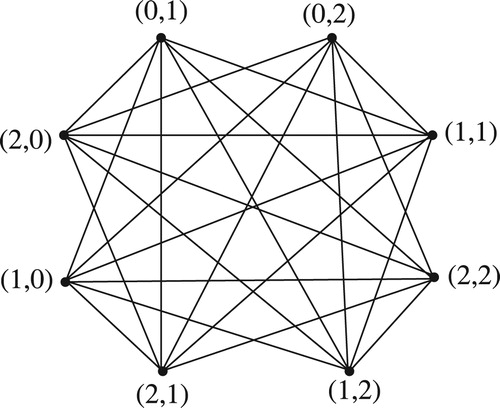
Conversely, suppose or . Then is a subgraph of and by Theorem 1.1, . If , then and so . By Figs. 1a and 1b, . Since is isomorphic and .  □

The following theorems are used in Theorem 2.7.

Theorem 2.5

[2]

Let be a finite non-cyclic group. Then . Moreover , where is the number of maximal cyclic subgroups of .

Theorem 2.6

See [11]

Let be a finite -group for some prime . Then if and only if is either a cyclic group or a generalized quaternion group.

A covering for a group is a collection of proper subgroups of whose union is . For , an -cover for a group is a cover with members. A cover is irredundant if no proper subcollection is also a cover. We write for the largest index over all groups G having an irredundant -cover with intersection . Abdollahi et al. obtained (see [12]). We use these results to prove the following theorem.

Theorem 2.7

Let be a finite non-cyclic group. Then if and only if is isomorphic to one of the following groups: or .

Proof

Assume that . Suppose that . Let such that is non-cyclic. Since is non-locally cyclic finite group, there exists and so is a subgraph of the graph induced by the elements of in . Hence .

Suppose that . Suppose is not a -group, where is prime. Then there exists an element such that . Since is non-empty, there exists such that is non-cyclic. Therefore , makes a subgraph isomorphic to , which is a contradiction. Thus for all . Since , is a 2-group and so by Theorem 2.3, for some . By Theorem 2.6 and by hypothesis, is a generalized quaternion group and contains an element of order . If , then there exist and in such that is non-cyclic and so , makes a subgraph isomorphic to , which is a contradiction. Therefore and so , a contradiction. Hence .

If contains an element such that , then where is a suitable power of such that and , makes a subgraph isomorphic to , which is a contradiction. Therefore , that is . Since and by Theorem 2.5, contains at most 6 maximal cyclic subgroups. But . Thus . Since , . Since where .

Now we consider the following cases.

(i) If , then or 3. Then is isomorphic to , , . If , then contains 8 vertices and 24 edges. Then by Theorem 1.4, , which contradicts to our hypothesis. If , then by Theorem 2.1, is a clique of , which is not possible. Since is a subgraph of , .

(ii) If , then or 2. If , then and is isomorphic to , which is a contradiction. Suppose , then is isomorphic to and by (i), .

(iii) If , then or 2. If , then is isomorphic to . Since every element of order 2 is adjacent to every element of order 3, is a subgraph of and hence . Suppose , then there is no group that satisfies the required conditions.

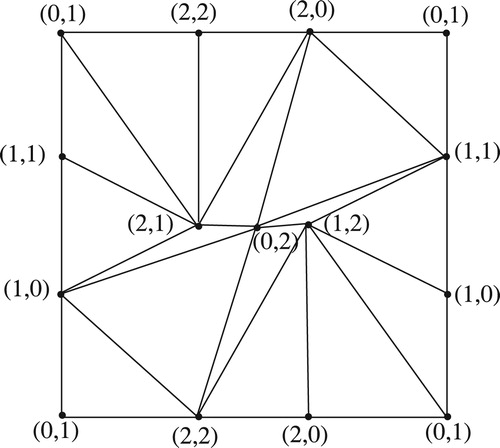
(iv) If , then . If , then is isomorphic to or . Since is a subgraph of (see Figs. 2a and 2b) and by Fig. 3, or . By Theorem 2.1, is isomorphic to and hence , which is not possible. If , then is isomorphic to . Since is a subgraph of , .

(v) If , then must be 0 and so or 2⁵. If , then is isomorphic to the following groups.

If is isomorphic to , then by Theorem 2.1, and so , which is a contradiction. If is isomorphic to the remaining groups, we can find a suitable set of vertices such that they make as a subgraph and so .

If , then is isomorphic to the following groups (see [13]). But it is easily seen that contains either or as a subgraph, which completes the proof. □

Fig. 3 Embedding of in .

Notes

Peer review under responsibility of Kalasalingam University.