Hybrid methods for a finite family of G-nonexpansive mappings in Hilbert spaces endowed with graphs

Peer review under responsibility of Kalasalingam University.

Abstract

In this paper, we prove a strong convergence theorem for two different hybrid methods by using CQ method for a finite family of G-nonexpansive mappings in a Hilbert space. We give an example and numerical results for supporting our main results and compare the rate of convergence of the two iterative methods.

Keywords:

• Hybrid method
• Fixed point
• G-nonexpansive mapping
• Directed graph

1 Introduction

Let $H$ be a Hilbert space with the inner product $〈.,.〉$, norm $\Vert .\Vert$ and $C$ be a nonempty subset of $H$. A nonlinear mapping $T:C\to C$ is said to be

1. contraction if there exists $\alpha \in (0,1)$ such that $\Vert Tx-Ty\Vert \le \alpha \Vert x-y\Vert$ for all $x,y\in C$;

2. nonexpansive if $\Vert Tx-Ty\Vert \le \Vert x-y\Vert$ for all $x,y\in C$.

The fixed point set of $T$ is denoted by $F\left(T\right)$, that is, $F\left(T\right)=\{x\in C:x=Tx\}$.

Since 1922, fixed point theorems and the existence of fixed points of a single-valued nonlinear mapping have been intensively studied and considered by many authors (see, for examples [1–7^{[1][2][3][4][5][6][7]}]).

In 1953, Mann [8] introduced the famous iteration procedure as follows: $x_1\in C,x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)T{x}_n,\forall n\in \mathbb{N}$where $\left\{{\alpha }_n\right\}\subset [0,1]$ and $\mathbb{N}$ the set of all positive integers. Many researchers have used Mann’s iteration for obtaining weak convergence theorem (see for example [9–11]).

In 2003, Nakajo and Takahashi [12] introduced a modification of the Mann iteration and called it CQ method. They generated the sequence $\left\{x_n\right\}$ by (1.1) $\left\{\begin{array}{cc}\hfill x_0& =x\in C,\hfill \\ \hfill y_n& ={\alpha }_n{x}_n+(1-{\alpha }_n)T{x}_n,\hfill \\ \hfill C_n& =\{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n& =\{z\in C:〈x_n-z,x_0-x_n〉\le 0\},\hfill \\ \hfill x_{n+1}& =P_{C_n\cap Q_n}{x}_0,n\ge 1,\hfill \end{array}\right.$(1.1) for $n\in \mathbb{N}\cup \left\{0\right\}$, where $\left\{{\alpha }_n\right\}\subset [0,a]$ for some $a\in [0,1)$. They showed that $\left\{x_n\right\}$ converges strongly to $P_{F\left(T\right)}{x}_0$.

In 2015, Khan et al. [13] used the following definition defined by Berinde [14] to compare the convergence rate:

Let $\left\{a_n\right\}$ and $\left\{b_n\right\}$ be two sequences of real numbers with limits $a$ and $b$, respectively. Assume that there exists ${lim}_{n\to \infty }\frac{|a_n-a|}{|b_n-b|}=\ell$. If $\ell =0$, then we say that $\left\{a_n\right\}$converges faster to $a$ than $\left\{b_n\right\}$ to $b$.

Let $C$ be a nonempty subset of a real Banach space $X$. Let $△$ denote the diagonal of the cartesian product $C\times C$. Consider a directed graph $G$ such that the set $V\left(G\right)$ of its vertices coincides with $C$, and the set $E\left(G\right)$ of its edges with $△\subseteq E\left(G\right)$. We assume $G$ has no parallel edge. So we can identify the graph $G$ with the pair $(V\left(G\right),E\left(G\right))$. A mapping $T:C\to C$ is said to be

1. G-contraction if $T$ satisfies the conditions:

(i) $T$ preserves edges of $G$, i.e., $(x,y)\in E\left(G\right)\Rightarrow (Tx,Ty)\in E\left(G\right),\forall (x,y)\in E\left(G\right);$

(ii) $T$ decreases weights of edges of $G$ in the following way: there exists $\alpha \in (0,1)$ such that $(x,y)\in E\left(G\right)\Rightarrow \Vert Tx-Ty\Vert \le \alpha \Vert x-y\Vert ,\forall (x,y)\in E\left(G\right);$

2. G-nonexpansive if $T$ satisfies the conditions:

(i) $T$ preserves edges of $G$, i.e., $(x,y)\in E\left(G\right)\Rightarrow (Tx,Ty)\in E\left(G\right),\forall (x,y)\in E\left(G\right);$

(ii) $T$ non-increases weights of edges of $G$ in the following way: $(x,y)\in E\left(G\right)\Rightarrow \Vert Tx-Ty\Vert \le \Vert x-y\Vert ,\forall (x,y)\in E\left(G\right).$

In 2008, Jachymski [15] proved some generalizations of the Banach’s contraction principle in complete metric spaces endowed with a graph. To be more precise, Jachymski proved the following result.

Theorem 1.1

[15]

Let $(X,d)$ be a complete metric space, and a triple $(X,d,G)$ has the following property:

for any sequence $\left\{x_n\right\}$ if $x_n\to x$ and $(x_n,x_{n+1})\in E\left(G\right)$ for $n\in \mathbb{N}$ and there is the subsequence $\left\{x_{n_k}\right\}$of $\left\{x_n\right\}$ with $(x_{n_k},x)\in E\left(G\right)$ for $n\in \mathbb{N}$.

Let $T:X\to X$ be a G-contraction, and $X_T=\{x\in X:(x,Tx)\in E\left(G\right)\}$. Then $F\left(T\right)\ne \varnothing$ if and only if $X_T\ne \varnothing$.

When $\left\{x_n\right\}$ is a sequence in $X$, we denote the strong convergence of $\left\{x_n\right\}$ to $x\in X$ by $x_n\to x$ and the weak convergence by $x_n\rightharpoonup x$.

In 2015, Tiammee et al. [16] and Alfuraidan [17] employed the above theorem to establish the existence and the convergence results for G-nonexpansive mappings with graphs.

Motivated by Nakajo and Takahashi [12] and Tiammee et al. [16], we introduce the modified CQ method for proving a strong convergence theorem for G-nonexpansive mappings in a Hilbert space endowed with a directed graph. Moreover, we provide some numerical examples to support our main theorem.

2 Preliminaries and lemmas

Let $C$ be a nonempty, closed and convex subset of a Hilbert space $H$. The nearest point projection of $H$ onto $C$ is denoted by $P_C$, that is, $\Vert x-P_{C}x\Vert \le \Vert x-y\Vert$ for all $x\in H$ and $y\in C$. Such $P_C$ is called the metric projection of $H$ onto $C$. We know that the metric projection $P_C$ is firmly nonexpansive, i.e., $\Vert P_{C}x-P_{C}y{\Vert }^2\le 〈P_{C}x-P_{C}y,x-y〉$for all $x,y\in H$. Furthermore, $〈x-P_{C}x,y-P_{C}x〉\le 0$ holds for all $x\in H$ and $y\in C$; see [18].

A mapping $A:C\to H$ is called $\alpha$-inverse strongly monotone if there exists a positive real number $\alpha$ such that $〈Ax-Ay,x-y〉\ge \alpha \Vert Ax-Ay{\Vert }^2,\forall x,y\in C.$We know that if $T:C\to C$ is nonexpansive, then $A=I-T$ is $\frac{1}{2}$-inverse strongly monotone; see [19] for more details. We consider the following variational inequality problem: find a $\hat{x}\in C$ such that $〈A\hat{x},\hat{x}-y〉\ge 0,\forall y\in C.$The set of solutions of the variational inequality (2.1) is denoted by $VI(C,A)$.

We need the following known results.

Lemma 2.1

[18]

Let $H$ be a real Hilbert space. Then $\Vert tx+(1-t)y{\Vert }^2=t\Vert x{\Vert }^2+(1-t)\Vert y{\Vert }^2-t(1-t)\Vert x-y{\Vert }^2,$ for all $t\in [0,1]$ and $x,y\in H$.

Lemma 2.2

[20]

Let $C$ be a nonempty, closed and convex subset of a real Hilbert space $H$. Given that $x,y,z\in H$ and $a\in \mathbb{R}$, the set $\{v\in C:\Vert y-v{\Vert }^2\le \Vert x-v{\Vert }^2+〈z,v〉+a\}$ is convex and closed.

Lemma 2.3

[12]

Let $C$ be a nonempty, closed and convex subset of a real Hilbert space $H$ and $P_C:H\to C$ be the metric projection from $H$ onto $C$. Then the following inequality holds: $\Vert y-P_{C}x{\Vert }^2+\Vert x-P_{C}x{\Vert }^2\le \Vert x-y{\Vert }^2,\forall x\in H,\forall y\in C.$

Lemma 2.4

[21]

Let $H$ be a real Hilbert space and let ${\left\{x_i\right\}}_{i=1}^m\subseteq H$. For ${\alpha }_i\in (0,1),i=1,2,\dots ,m$ such that ${\sum }_{i=1}^m{\alpha }_i=1$, the following identity holds: ${\Vert \sum _{i=1}^m{\alpha }_i{x}_i\Vert }^2=\sum _{i=1}^m{\alpha }_i\Vert x_i{\Vert }^2-\sum _{1\le i<j\le m}{\alpha }_i{\alpha }_j\Vert x_i-x_j{\Vert }^2.$

Lemma 2.5

Let $C$ be a nonempty subset of a Hilbert space $H$ and $G=(V\left(G\right),E\left(G\right))$ a directed graph such that $V\left(G\right)=C$. Let $T:C\to C$ be a G-nonexpansive mapping. Then, for any $\epsilon >0$, there exists a positive number $\xi \left(\epsilon \right)>0$ such that $\Vert x-Tx\Vert <\epsilon$ for all $x\in co\left(\{x_0,x_1\}\right)$, whenever $x_0,x_1\in C$ with $(x_0,x),(x_1,x)\in E\left(G\right)$, $\Vert x_0-T{x}_0\Vert \le \xi \left(\epsilon \right)$ and $\Vert x_1-T{x}_1\Vert \le \xi \left(\epsilon \right)$.

Proof

Let $x=(1-\lambda )x_0+\lambda x_1$, for some $\lambda \in [0,1]$ and $\epsilon >0$.

We consider the following two cases.

Case I. If $\Vert x_0-x_1\Vert <\frac{\epsilon }{3}$, then $\Vert x-x_0\Vert =\lambda \Vert x_0-x_1\Vert <\frac{\epsilon }{3}.$If $\xi \left(\epsilon \right)<\frac{\epsilon }{3}$, then we have

$\Vert Tx-x\Vert \le \Vert Tx-T{x}_0\Vert +\Vert T{x}_0-x_0\Vert +\Vert x_0-x\Vert \le 2\Vert x-x_0\Vert +\Vert T{x}_0-x_0\Vert <2\left(\frac{\epsilon }{3}\right)+\xi \left(\epsilon \right)<\epsilon .$

Case II. If $\Vert x_0-x_1\Vert \ge \frac{\epsilon }{3}$, then for any nonnegative number $\lambda <\frac{\epsilon }{3\Vert x_0-x_1\Vert }$, we have $\Vert x-x_0\Vert =\lambda \Vert x_0-x_1\Vert <\frac{\epsilon }{3}.$If $\xi \left(\epsilon \right)<\frac{\epsilon }{3}$ and $\lambda <\frac{\epsilon }{3\Vert x_0-x_1\Vert }$, then we have

$\Vert Tx-x\Vert \le \Vert Tx-T{x}_0\Vert +\Vert T{x}_0-x_0\Vert +\Vert x_0-x\Vert \le 2\Vert x-x_0\Vert +\Vert T{x}_0-x_0\Vert <2\left(\frac{\epsilon }{3}\right)+\xi \left(\epsilon \right)<\epsilon .$

We may assume that $\lambda \in [\frac{\epsilon }{3\Vert x_0-x_1\Vert },1]$ and $\Vert x_0-x_1\Vert \ge \frac{\epsilon }{3}$. Then we obtain

(2.1) $\Vert Tx-x_0\Vert \le \Vert Tx-T{x}_0\Vert +\Vert T{x}_0-x_0\Vert \le \Vert x-x_0\Vert +\xi \left(\epsilon \right)=\lambda \Vert x_1-x_0\Vert +\xi \left(\epsilon \right)$(2.1)

and

(2.2) $\Vert Tx-x_1\Vert \le \Vert Tx-T{x}_1\Vert +\Vert T{x}_1-x_1\Vert \le \Vert x-x_1\Vert +\xi \left(\epsilon \right)=(1-\lambda )\Vert x_1-x_0\Vert +\xi \left(\epsilon \right).$(2.2)

From (2.1), (2.2) and $\lambda \in [\frac{\epsilon }{3\Vert x_0-x_1\Vert },1]$, we get that

$\Vert Tx-x\Vert \le (1-\lambda )\Vert Tx-x_0\Vert +\lambda \Vert Tx-x_1\Vert \le 2(1-\lambda )\lambda \Vert x_1-x_0\Vert +\xi \left(\epsilon \right)<\epsilon .\square$

We next prove the demiclosedness principle of a G-nonexpansive mapping.

Lemma 2.6

Let $C$ be a nonempty, closed and convex subset of a Hilbert space $H$ and $G=(V\left(G\right),E\left(G\right))$ a directed graph such that $V\left(G\right)=C$. Let $T:C\to C$ be a G-nonexpansive mapping and $\left\{x_n\right\}$ be a sequence in $C$ such that $x_n\rightharpoonup x$ for some $x\in C$. If, there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$such that $(x_{n_k},x)\in E\left(G\right)$ for all $k\in \mathbb{N}$ and $\{x_n-T{x}_n\}\to y$ for some $y\in H$, then $(I-T)x=y$.

Proof

Let $\left\{x_n\right\}$ be a sequence in $C$ such that $x_n\rightharpoonup x$ and ${lim}_{n\to \infty }\Vert x_n-T{x}_n-y\Vert =0$ for some $y\in H$. Set $T_{y}x=Tx+y$, $x\in C$. Then $(I-T_y)x_n=(I-T)x_n-y$. We may assume, without loss of generality, that $y=0$. By the assumption, there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $(x_{n_k},x)\in E\left(G\right)$. We set ${\epsilon }_{n_k}=\Vert x_{n_k}-T{x}_{n_k}\Vert$. Let $\epsilon >0$. Since ${\epsilon }_{n_k}\to 0$ as $k\to \infty$, there exists $N\in \mathbb{N}$ such that ${\epsilon }_{n_k}<\epsilon ,\forall k\ge N.$Lemma 2.5 gives that, for each $z\in \overline{co}\left(\{x_{n_k}:k\ge N\}\right)$, $\Vert z-Tz\Vert <\epsilon$. By the weak compactness of $\overline{co}\left(\{x_{n_k}:k\ge N\}\right)$, it contains the weak limit $x$ of $\left\{x_{n_k}\right\}$. This shows that $\Vert x-Tx\Vert <\epsilon$. Hence $\Vert x-Tx\Vert =0$, that is, $x=Tx$, since $\epsilon$ is arbitrary.  □

3 Main results

In this section, by using the CQ method, we obtain two different strong convergence theorems for finding the same common fixed point of a finite family of G-nonexpansive mappings in real Hilbert spaces.

Theorem 3.1

Let $C$ be a nonempty closed and convex subset of a real Hilbert space $H$ and let $G=(V\left(G\right),E\left(G\right))$ be a directed graph such that $V\left(G\right)=C$ and $E\left(G\right)$ is convex. Let $\{T_i:i=1,2,\dots ,N\}$ be a finite family of G-nonexpansive mappings of $C$ into itself. Assume that $F≔{\bigcap }_{i=1}^{N}F\left(T_i\right)\ne \varnothing$, $F$ is closed and $F\left(T_i\right)\times F\left(T_i\right)\subseteq E\left(G\right)$ for all $i\in \{1,2,\dots ,N\}$. For an initial point $x_1\in H$ with $Q_1=C$, let $\left\{x_n\right\}$ be a sequence generated by (3.1) $\left\{\begin{array}{cc}\hfill y_{i,n}=& {\alpha }_{i,n}{x}_n+(1-{\alpha }_{i,n})T_i{x}_n,\hfill \\ \hfill C_{i,n}=& \{z\in C:\Vert y_{i,n}-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill C_n=& \bigcap _{i=1}^N{C}_{i,n},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.1) where $\left\{{\alpha }_{i,n}\right\}\subset [0,1)$ for all $i\in \{1,2,\dots ,N\}$such that ${lim\; sup}_{n\to \infty }{\alpha }_{i,n}<1$ for all $i\in \{1,2,\dots ,N\}$. Assume that $\left\{x_n\right\}$ dominates $z$ for all $z\in F$ and if there exists a subsequence $\left\{x_{n_k}\right\}$of $\left\{x_n\right\}$ such that $x_{n_k}\rightharpoonup w\in C$, then $(x_{n_k},w)\in E\left(G\right)$. Then the sequence $\left\{x_n\right\}$ converges strongly to $P_F{x}_1.$

Proof

We split the proof into six steps.

Step 1. Show that $P_F{x}_1$ is well-defined for each $x_1\in H.$

As shown in Theorem 3.2 of Tiammee et al. [16], $F\left(T_i\right)$ is convex for all $i=1,2,\dots ,N$. It follows now from the assumption that $F={\bigcap }_{i=1}^{N}F\left(T_i\right)$ is closed and convex. Hence, $P_F{x}_1$ is well-defined.

Step 2. Show that $P_{C_n\cap Q_n}{x}_1$ is well-defined for each $x_1\in H.$

From the definition of $C_n$ and $Q_n$, it is obvious that $Q_n$ is closed and convex for all $n\in \mathbb{N}$. It follows from Lemma 2.2 that for each $i\in \{1,2,\dots ,N\}$, $C_{i,n}$ is closed and convex for all $n\in \mathbb{N}$. This implies that $C_n$ is also closed and convex for all $n\in \mathbb{N}$. Let $p\in F$ and $i\in \{1,2,\dots ,N\}$. Since $\left\{x_n\right\}$ dominates $p$, we have

(3.2) $\Vert y_{i,n}-p\Vert \le {\alpha }_{i,n}\Vert x_n-p\Vert +(1-{\alpha }_{i,n})\Vert T_i{x}_n-p\Vert \le \Vert x_n-p\Vert .$(3.2)

So, we have $p\in C_{i,n}$ for all $i=1,2,\dots ,N$ and $n\in \mathbb{N}$. We can conclude that $p\in {\bigcap }_{i=1}^N{C}_{i,n}=C_n$ for all $n\in \mathbb{N}$. Thus $F\subset C_n$ for all $n\in \mathbb{N}$. Using induction, it can be shown as in [22] that $F\subset Q_n$ for all $i=1,2,\dots ,N$. Hence $F\subset C_n\cap Q_n$. This implies that $P_{C_n\cap Q_n}{x}_1$ is well-defined.

Step 3. Show that ${lim}_{n\to \infty }\Vert x_n-x_1\Vert$ exists.

Since $F$ is a nonempty, closed and convex subset of $H$, there exists a unique $v\in F$ such that $v=P_F{x}_1.$ From $x_n=P_{Q_n}{x}_1$ and $x_{n+1}\in Q_n$, $\forall n\in \mathbb{N}$, we get (3.3) $\Vert x_n-x_1\Vert \le \Vert x_{n+1}-x_1\Vert ,\forall n\in \mathbb{N}.$(3.3) On the other hand, as $F\subset Q_n$, we obtain (3.4) $\Vert x_n-x_1\Vert \le \Vert v-x_1\Vert ,\forall n\in \mathbb{N}.$(3.4) It follows from (3.3)(3.3) $\Vert x_n-x_1\Vert \le \Vert x_{n+1}-x_1\Vert ,\forall n\in \mathbb{N}.$(3.3) and (3.4(3.4) $\Vert x_n-x_1\Vert \le \Vert v-x_1\Vert ,\forall n\in \mathbb{N}.$(3.4) ) that the sequence $\left\{x_n\right\}$ is bounded and nondecreasing. Therefore ${lim}_{n\to \infty }\Vert x_n-x_1\Vert$ exists.

Step 4. Show that $x_n\to w\in C$ as $n\to \infty$.

For $m>n$, by the definition of $Q_n$, we see that $Q_m\subset Q_n$. Noting that $x_m=P_{Q_m}{x}_1$ and $x_n=P_{Q_n}{x}_1$, by Lemma 2.3, we get $\Vert x_m-x_n{\Vert }^2\le \Vert x_m-x_1{\Vert }^2-\Vert x_n-x_1{\Vert }^2.$From Step 3, we obtain that $\left\{x_n\right\}$ is a Cauchy sequence. Hence, there exists $w\in C$ such that $x_n\to w$ as $n\to \infty$. In particular, we have (3.5) $\underset{n\to \infty }{lim}\Vert x_{n+1}-x_n\Vert =0.$(3.5) Step 5. Show that $w\in F$.

Since $x_{n+1}\in Q_n$, it follows from (3.5(3.5) $\underset{n\to \infty }{lim}\Vert x_{n+1}-x_n\Vert =0.$(3.5) ) that (3.6) $\Vert y_{i,n}-x_n\Vert \le \Vert y_{i,n}-x_{n+1}\Vert +\Vert x_{n+1}-x_n\Vert \le 2\Vert x_{n+1}-x_n\Vert \to 0$(3.6) as $n\to \infty$ for all $i=1,2,\dots ,N$. Since $y_{i,n}={\alpha }_{i,n}{x}_n+(1-{\alpha }_{i,n})T_i{x}_n$, we have $\Vert x_n-T_i{x}_n\Vert =\frac{1}{(1-{\alpha }_{i,n})}\Vert y_{i,n}-x_n\Vert .$It follows from ${lim\; sup}_{n\to \infty }{\alpha }_{i,n}<1$ for all $i=1,2,\dots ,N$ and (3.6(3.6) $\Vert y_{i,n}-x_n\Vert \le \Vert y_{i,n}-x_{n+1}\Vert +\Vert x_{n+1}-x_n\Vert \le 2\Vert x_{n+1}-x_n\Vert \to 0$(3.6) ) that (3.7) $\Vert x_n-T_i{x}_n\Vert \to 0$(3.7) as $n\to \infty$ for all $i\in \{1,2,\dots ,N\}$. From $(x_n,w)\in E\left(G\right)$ and Lemma 2.6, we have $w\in F$.

Step 6. Show that $w=v=P_F{x}_1$.

Since $x_n=P_{Q_n}{x}_1$, we have (3.8) $〈x_1-x_n,x_n-p〉\ge 0,\forall p\in Q_n.$(3.8) By taking the limit in (3.8(3.8) $〈x_1-x_n,x_n-p〉\ge 0,\forall p\in Q_n.$(3.8) ), we obtain (3.9) $〈x_1-w,w-p〉\ge 0,\forall p\in Q_n.$(3.9) Since $F\subset Q_n$, so $w=v=P_F{x}_1$. This completes the proof.  □

Theorem 3.2

Let $C$ be a nonempty closed and convex subset of a real Hilbert space $H$ and let $G=(V\left(G\right),E\left(G\right))$ be a directed graph such that $V\left(G\right)=C$ and $E\left(G\right)$ is convex. Let $\{T_i:i=1,2,\dots ,N\}$ be a finite family of G-nonexpansive mappings of $C$ into itself. Assume that $F={\bigcap }_{i=1}^{N}F\left(T_i\right)\ne \varnothing$, $F$ is closed and $F\left(T_i\right)\times F\left(T_i\right)\subseteq E\left(G\right)$ for all $i\in \{1,2,\dots ,N\}$. For an initial point $x_1\in H$ with $Q_1=C$, let $\left\{x_n\right\}$ be a sequence generated by (3.10) $\left\{\begin{array}{cc}\hfill y_n=& {\alpha }_{0,n}{x}_n+\sum _{i=1}^N{\alpha }_{i,n}{T}_i{x}_n,\hfill \\ \hfill C_n=& \{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.10) where $\left\{{\alpha }_{i,n}\right\}\subset (0,1]$ for all $i\in \{0,1,2,\dots ,N\}$such that ${\sum }_{i=0}^N{\alpha }_{i,n}=1$ and ${lim\; inf}_{n\to \infty }{\alpha }_{0,n}{\alpha }_{i,n}>0$ for all $i\in \{1,2,\dots ,N\}$. Assume that $\left\{x_n\right\}$ dominates $z$ for all $z\in F$ and if there exists a subsequence $\left\{x_{n_k}\right\}$of $\left\{x_n\right\}$ such that $x_{n_k}\rightharpoonup w\in C$, then $(x_{n_k},w)\in E\left(G\right)$. Then the sequence $\left\{x_n\right\}$ converges strongly to $P_F{x}_1.$

Proof

From Step 1 in the proof of Theorem 3.1, we have that $P_F{x}_1$ is well-defined for each $x_1\in H$. We know from Step 2 in the proof of Theorem 3.1 that $C_n\cap Q_n$ is closed and convex for all $n\in \mathbb{N}$. Let $p\in F$. Since $\left\{x_n\right\}$ dominates $p$, we have

$\Vert y_n-p\Vert =∥{\alpha }_{0,n}{x}_n+\sum _{i=1}^N{\alpha }_{i,n}{T}_i{x}_n∥\le {\alpha }_{0,n}\Vert x_n-p\Vert +\sum _{i=1}^N{\alpha }_{i,n}\Vert T_i{x}_n-p\Vert \le \Vert x_n-p\Vert .$

So, we have $p\in C_n$ for all $n\in \mathbb{N}$. Thus $F\subset C_n$ for all $n\in \mathbb{N}$. It is clear that $F\subset Q_n$ for all $n\in \mathbb{N}$ (see Marino and Xu [22]). Hence, $F\subset C_n\cap Q_n$ for all $n\in \mathbb{N}$. This implies that $P_{C_n\cap Q_n}{x}_1$ is well-defined. As in Steps 3–4 of the proof of Theorem 3.1, we have that the sequence $\left\{x_n\right\}$ is Cauchy. By the completeness of the space $H$, $x_n\to w\in C$ as $n\to \infty$. We next show that $w\in F$. Since $x_{n+1}\in Q_n$ and $\left\{x_n\right\}$ is Cauchy, it follows that (3.11) $\Vert y_n-x_n\Vert \le \Vert y_n-x_{n+1}\Vert +\Vert x_{n+1}-x_n\Vert \le 2\Vert x_{n+1}-x_n\Vert \to 0$(3.11) as $n\to \infty$. For $p\in F$, it follows from Lemma 2.4 and $\left\{x_n\right\}$ dominates $p$ that

$\Vert y_n-p{\Vert }^2={∥{\alpha }_{0,n}{x}_n+\sum _{i=1}^N{\alpha }_{i,n}{T}_i{x}_n∥}^2={\alpha }_{0,n}\Vert x_n-p{\Vert }^2+\sum _{i=1}^N{\alpha }_{i,n}\Vert T_i{x}_n-p{\Vert }^2-\sum _{i=1}^N{\alpha }_{0,n}{\alpha }_{i,n}\Vert T_i{x}_n-x_n{\Vert }^2\le \Vert x_n-p{\Vert }^2-\sum _{i=1}^N{\alpha }_{0,n}{\alpha }_{i,n}\Vert T_i{x}_n-x_n{\Vert }^2.$

This implies that $\sum _{i=1}^N{\alpha }_{0,n}{\alpha }_{i,n}\Vert T_i{x}_n-x_n{\Vert }^2\le \Vert x_n-p{\Vert }^2-\Vert y_n-p{\Vert }^2.$It follows from the assumption and (3.11(3.11) $\Vert y_n-x_n\Vert \le \Vert y_n-x_{n+1}\Vert +\Vert x_{n+1}-x_n\Vert \le 2\Vert x_{n+1}-x_n\Vert \to 0$(3.11) ), we obtain $\underset{n\to \infty }{lim}\Vert T_i{x}_n-x_n\Vert =0$for all $i=1,2,\dots ,N$. From $(x_n,w)\in E\left(G\right)$ and Lemma 2.6, we have $w\in F$. As in Step 6 of the proof of Theorem 3.1, we obtain $w=P_F{x}_1$. This completes the proof.  □

Remark 3.3

The sequences $\left\{x_n\right\}$ generated in Theorem 3.1 and 3.2 converge to $P_F{x}_1$ under the different conditions on the sequence ${\alpha }_{i,n}$.

We know that every G-nonexpansive mapping is nonexpansive [16], then we obtain the following results.

Corollary 3.4

Let $C$ be a nonempty closed and convex subset of a real Hilbert space $H$. Let $\{T_i:i=1,2,\dots ,N\}$be a finite family of nonexpansive mappings of $C$ into itself. Assume that $F≔{\bigcap }_{i=1}^{N}F\left(T_i\right)\ne \varnothing$. For an initial point $x_1\in H$ with $Q_1=C$, let $\left\{x_n\right\}$ be a sequence generated by (3.12) $\left\{\begin{array}{cc}\hfill y_{i,n}=& {\alpha }_{i,n}{x}_n+(1-{\alpha }_{i,n})T_i{x}_n,\hfill \\ \hfill C_{i,n}=& \{z\in C:\Vert y_{i,n}-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill C_n=& \bigcap _{i=1}^N{C}_{i,n},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.12) where $\left\{{\alpha }_{i,n}\right\}\subset [0,1)$ for all $i\in \{1,2,\dots ,N\}$. Assume that ${lim\; sup}_{n\to \infty }{\alpha }_{i,n}<1$ for all $i\in \{1,2,\dots ,N\}.$ Then the sequence $\left\{x_n\right\}$ converges strongly to $P_F{x}_1.$

Corollary 3.5

Let $C$ be a nonempty closed and convex subset of a real Hilbert space $H$. Let $\{T_i:i=1,2,\dots ,N\}$be a finite family of nonexpansive mappings of $C$ into itself. Assume that $F={\bigcap }_{i=1}^{N}F\left(T_i\right)\ne \varnothing$. For an initial point $x_1\in H$ with $Q_1=C$, let $\left\{x_n\right\}$ be a sequence generated by (3.13) $\left\{\begin{array}{cc}\hfill y_n=& {\alpha }_{0,n}{x}_n+\sum _{i=1}^N{\alpha }_{i,n}{T}_i{x}_n,\hfill \\ \hfill C_n=& \{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.13) where $\left\{{\alpha }_{i,n}\right\}\subset (0,1]$ for all $i\in \{0,1,2,\dots ,N\}$such that ${\sum }_{i=0}^N{\alpha }_{i,n}=1$. Assume that ${lim\; inf}_{n\to \infty }{\alpha }_{0,n}{\alpha }_{i,n}>0$ for all $i\in \{1,2,\dots ,N\}.$ Then the sequence $\left\{x_n\right\}$ converges strongly to $P_F{x}_1.$

Putting $T_i=I(i=2,3,\dots ,N)$ where $I$ is an identity mapping in Theorem 3.1 –3.2, we obtain the following result.

Corollary 3.6

Let $C$ be a nonempty closed and convex subset of a real Hilbert space $H$ and let $G=(V\left(G\right),E\left(G\right))$ be a directed graph such that $V\left(G\right)=C$ and $E\left(G\right)$ is convex. Let $T$ be a G-nonexpansive mapping of $C$ into itself. Assume that $F\left(T\right)\ne \varnothing$, $F\left(T\right)$ is closed and $F\left(T\right)\times F\left(T\right)\subseteq E\left(G\right)$. For an initial point $x_1\in H$ with $Q_1=C$, let $\left\{x_n\right\}$ be a sequence generated by (3.14) $\left\{\begin{array}{cc}\hfill y_n=& {\alpha }_n{x}_n+(1-{\alpha }_n)T{x}_n,\hfill \\ \hfill C_n=& \{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.14) where $\left\{{\alpha }_n\right\}\subset (0,1]$ such that ${lim\; sup}_{n\to \infty }{\alpha }_n<1$. Assume that $\left\{x_n\right\}$ dominates $z$ for all $z\in F\left(T\right)$ and if there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$such that $x_{n_k}\rightharpoonup w\in C$, then $(x_{n_k},w)\in E\left(G\right)$. Then the sequence $\left\{x_n\right\}$ converges strongly to $P_{F\left(T\right)}{x}_1.$

Remark 3.7

The iterative scheme (3.14(3.14) $\left\{\begin{array}{cc}\hfill y_n=& {\alpha }_n{x}_n+(1-{\alpha }_n)T{x}_n,\hfill \\ \hfill C_n=& \{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.14) ) extends the CQ method (1.1(1.1) $\left\{\begin{array}{cc}\hfill x_0& =x\in C,\hfill \\ \hfill y_n& ={\alpha }_n{x}_n+(1-{\alpha }_n)T{x}_n,\hfill \\ \hfill C_n& =\{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n& =\{z\in C:〈x_n-z,x_0-x_n〉\le 0\},\hfill \\ \hfill x_{n+1}& =P_{C_n\cap Q_n}{x}_0,n\ge 1,\hfill \end{array}\right.$(1.1) ) from a nonexpansive mapping to a G-nonexpansive mapping.

If $\lambda \in [0,2\alpha ]$, we know that $I-\lambda A$ is nonexpansive; see [19]. Then, we obtain the following results.

Corollary 3.8

Let $C$ be a nonempty closed and convex subset of a real Hilbert space $H$. Let $\{A_i:C\to H,i=1,2,\dots ,N\}$be a finite family of $\alpha$-inverse strongly monotone with ${\bigcap }_{i=1}^{N}V(C,A_i)\ne \varnothing$. For an initial point $x_1\in H$ with $Q_1=C$, let $\left\{x_n\right\}$ be a sequence generated by (3.15) $\left\{\begin{array}{cc}\hfill y_{i,n}=& {\alpha }_{i,n}{x}_n+(1-{\alpha }_{i,n})P_C(x_n-{\lambda }_n{A}_i{x}_n),\hfill \\ \hfill C_{i,n}=& \{z\in C:\Vert y_{i,n}-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill C_n=& \bigcap _{i=1}^N{C}_{i,n},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.15) where $\left\{{\alpha }_{i,n}\right\}\subset [0,1)$ for all $i\in \{1,2,\dots ,N\}$and $\left\{{\lambda }_n\right\}\subset [0,2\alpha ]$. Assume that ${lim\; sup}_{n\to \infty }{\alpha }_{i,n}<1$ for all $i\in \{1,2,\dots ,N\}.$ Then the sequence $\left\{x_n\right\}$ converges strongly to $P_{{\bigcap }_{i=1}^{N}V(C,A_i)}{x}_1.$

Corollary 3.9

Let $C$ be a nonempty closed and convex subset of a real Hilbert space $H$. Let $\{A_i:C\to H,i=1,2,\dots ,N\}$be a finite family of $\alpha$-inverse strongly monotone with ${\bigcap }_{i=1}^{N}V(C,A_i)\ne \varnothing$. For an initial point $x_1\in H$ with $Q_1=C$, let $\left\{x_n\right\}$ be a sequence generated by (3.16) $\left\{\begin{array}{cc}\hfill y_n=& {\alpha }_{0,n}{x}_n+\sum _{i=1}^N{\alpha }_{i,n}{P}_C(x_n-{\lambda }_n{A}_i{x}_n),\hfill \\ \hfill C_n=& \{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.16) where $\left\{{\alpha }_{i,n}\right\}\subset (0,1]$ for all $i\in \{0,1,2,\dots ,N\}$such that ${\sum }_{i=0}^N{\alpha }_{i,n}=1$ and $\left\{{\lambda }_n\right\}\subset [0,2\alpha ]$. Assume that ${lim\; inf}_{n\to \infty }{\alpha }_{0,n}{\alpha }_{i,n}>0$ for all $i\in \{1,2,\dots ,N\}.$ Then the sequence $\left\{x_n\right\}$ converges strongly to $P_{{\bigcap }_{i=1}^{N}V(C,A_i)}{x}_1.$

4 Examples and numerical results

In this section, we give examples and numerical results for supporting our main theorem.

Example 4.1

Let $H=\mathbb{R}$ and $C=[0,3]$. Assume that $(x,y)\in E\left(G\right)$ if and only if $0\le x,y\le 2$ or $x=y$. Define two mappings $T_1,T_2:C\to C$ by $T_{1}x=\frac{1}{4}tan(x-1)+1\text{and}{T}_{2}x=2^{\frac{3}{4}(x-1)},$for any $x\in C$. Let ${\alpha }_{1,n}=\frac{n}{3n+2}$ and ${\alpha }_{2,n}=\frac{n}{4n+3}$. It is easy to check that $T_1,T_2$ are G-nonexpansive. On the other hand, $T_1,T_2$ are not nonexpansive for $x=\frac{14}{5}$ and $y=2$. This implies that $|T_{1}x-T_{1}y|>\frac{4}{5}=|x-y|$ and $|T_{2}x-T_{2}y|>\frac{4}{5}=|x-y|$.

For $\left\{x_n\right\}$ generated by (3.1(3.1) $\left\{\begin{array}{cc}\hfill y_{i,n}=& {\alpha }_{i,n}{x}_n+(1-{\alpha }_{i,n})T_i{x}_n,\hfill \\ \hfill C_{i,n}=& \{z\in C:\Vert y_{i,n}-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill C_n=& \bigcap _{i=1}^N{C}_{i,n},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.1) ), we divide the process of our iteration into 3 Steps as follows:

Step 1. Find $C_n={\bigcap }_{i=1}^2{C}_{i,n}$. Since $C_{1,n}=\{z\in C:\Vert y_{1,n}-z\Vert \le \Vert x_n-z\Vert \}$ and $C_{2,n}=\{z\in C:\Vert y_{2,n}-z\Vert \le \Vert x_n-z\Vert \}$, we obtain that $(2z-(y_{1,n}+x_n))(x_n-y_{1,n})\le 0$ and $(2z-(y_{2,n}+x_n))(x_n-y_{2,n})\le 0.$ We observe the following cases:

Case 1 : If $x_n-y_{1,n}=0$, then $C_{1,n}=C$, $\forall n\ge 1.$

Case 2 : If $x_n-y_{1,n}>0$, then $z\le \frac{y_{1,n}+x_n}{2}$. Thus, $C_{1,n}=[0,\frac{y_{1,n}+x_n}{2}]$, $\forall n\ge 1.$

Case 3 : If $x_n-y_{1,n}<0$, then $z\ge \frac{y_{1,n}+x_n}{2}$. Thus, $C_{1,n}=[\frac{y_{1,n}+x_n}{2},3]$, $\forall n\ge 1.$

Similarly, we have $C_{2,n}=C$; where $x_n-y_{2,n}=0$, $C_{2,n}=[0,\frac{y_{2,n}+x_n}{2}]$; where $x_n-y_{2,n}>0$ and $C_{2,n}=[\frac{y_{2,n}+x_n}{2},3]$; where $x_n-y_{2,n}<0$, $\forall n\ge 1.$

Step 2. Find $Q_n=\{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\}=\{z\in Q_{n-1}:(x_1-x_n)(z-x_n)\le 0\}$. We observe the following cases:

Case 1 : If $x_1-x_n=0$, then $Q_n=C$, $\forall n\ge 2.$

Case 2 : If $x_1-x_n>0$, then $z\le x_n$. Thus, $Q_n=Q_{n-1}\cap [0,x_n]$ , $\forall n\ge 2.$

Case 3 : If $x_1-x_n<0$, then $z\ge x_n$. Thus, $Q_n=Q_{n-1}\cap [x_n,3]$ , $\forall n\ge 2$.

Step 3. Compute the numerical results of $x_{n+1}=P_{C_n\cap Q_n}{x}_1$. Choose $x_1=0$, we have

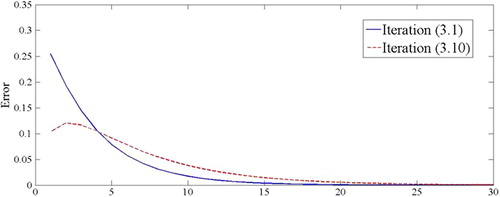
From Table 1, we see that $1$ is the solution of iteration (3.1(3.1) $\left\{\begin{array}{cc}\hfill y_{i,n}=& {\alpha }_{i,n}{x}_n+(1-{\alpha }_{i,n})T_i{x}_n,\hfill \\ \hfill C_{i,n}=& \{z\in C:\Vert y_{i,n}-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill C_n=& \bigcap _{i=1}^N{C}_{i,n},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.1) ).

We next show that our iteration generated by (3.10(3.10) $\left\{\begin{array}{cc}\hfill y_n=& {\alpha }_{0,n}{x}_n+\sum _{i=1}^N{\alpha }_{i,n}{T}_i{x}_n,\hfill \\ \hfill C_n=& \{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.10) ) also converges to 1. As the same above process, choose $x_1=0$. (See Table 2.)

From Table 2, we see that the iteration (3.10(3.10) $\left\{\begin{array}{cc}\hfill y_n=& {\alpha }_{0,n}{x}_n+\sum _{i=1}^N{\alpha }_{i,n}{T}_i{x}_n,\hfill \\ \hfill C_n=& \{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.10) ) converges to $1$. (See Fig. 1.)

Fig. 1 Error plots for sequences $\left\{x_n\right\}$ in Tables 1 and 2.

Table 1 Numerical results of iteration (3.1(3.1) $\left\{\begin{array}{cc}\hfill y_{i,n}=& {\alpha }_{i,n}{x}_n+(1-{\alpha }_{i,n})T_i{x}_n,\hfill \\ \hfill C_{i,n}=& \{z\in C:\Vert y_{i,n}-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill C_n=& \bigcap _{i=1}^N{C}_{i,n},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.1) ).

$n$	$y_{1,n}$	$y_{2,n}$	$C_n\cap Q_n$	$x_n$
1	0.48852	0.50966	[0.25483, 3.00000]	0.00000
2	0.64072	0.60174	[0.44777, 3.00000]	0.25483
3	0.73736	0.68992	[0.59257, 3.00000]	0.44777
4	0.80652	0.76353	[0.69955, 3.00000]	0.59257
5	0.85695	0.82151	[0.77825, 3.00000]	0.69955
6	0.89402	0.86604	[0.83613, 3.00000]	0.77825
7	0.92137	0.89978	[0.87875, 3.00000]	0.83613
8	0.94160	0.92516	[0.91018, 3.00000]	0.87875
9	0.95660	0.94418	[0.93339, 3.00000]	0.91018
10	0.96772	0.95839	[0.95055, 3.00000]	0.93339
⋮	⋮	⋮	⋮	⋮
30	0.99991	0.99988	[0.99986, 3.00000]	0.99981

Table 2 Numerical results of iteration (3.10(3.10) $\left\{\begin{array}{cc}\hfill y_n=& {\alpha }_{0,n}{x}_n+\sum _{i=1}^N{\alpha }_{i,n}{T}_i{x}_n,\hfill \\ \hfill C_n=& \{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.10) ).

$n$	$y_n$	$C_n\cap Q_n$	$x_n$
1	0.20707	[0.10354, 3.00000]	0.00000
2	0.34473	[0.22413, 3.00000]	0.10354
3	0.45763	[0.34088, 3.00000]	0.22413
4	0.55155	[0.44621, 3.00000]	0.34088
5	0.62963	[0.53792, 3.00000]	0.44621
6	0.69442	[0.61617, 3.00000]	0.53792
7	0.74809	[0.68213, 3.00000]	0.61617
8	0.79247	[0.73730, 3.00000]	0.68213
9	0.82913	[0.78321, 3.00000]	0.73730
10	0.85938	[0.82130, 3.00000]	0.78321
⋮	⋮	⋮	⋮
30	0.99731	[0.99655, 3.00000]	0.99579

In the same way of Khan ([13], Example 3), we can conclude the following remark.

Remark 4.2

We see that the iteration (3.1(3.1) $\left\{\begin{array}{cc}\hfill y_{i,n}=& {\alpha }_{i,n}{x}_n+(1-{\alpha }_{i,n})T_i{x}_n,\hfill \\ \hfill C_{i,n}=& \{z\in C:\Vert y_{i,n}-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill C_n=& \bigcap _{i=1}^N{C}_{i,n},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.1) ) converges faster than the iteration (3.10(3.10) $\left\{\begin{array}{cc}\hfill y_n=& {\alpha }_{0,n}{x}_n+\sum _{i=1}^N{\alpha }_{i,n}{T}_i{x}_n,\hfill \\ \hfill C_n=& \{z\in C:\Vert y_n-z\Vert \le \Vert x_n-z\Vert \},\hfill \\ \hfill Q_n=& \{z\in Q_{n-1}:〈x_1-x_n,z-x_n〉\le 0\},n\ge 2,\hfill \\ \hfill x_{n+1}=& P_{C_n\cap Q_n}{x}_1,n\ge 1,\hfill \end{array}\right.$(3.10) ) under the same conditions.

Notes

Peer review under responsibility of Kalasalingam University.