Edge odd graceful labeling of some path and cycle related graphs

Peer review under responsibility of Kalasalingam University.

Abstract

Solairaju and Chithra introduced a new type of labeling of a graph $G$ with $p$ vertices and $q$ edges called an edge odd graceful labeling if there is a bijection $f$ from the edges of the graph to the set $\{1,3,\dots ,2q-1\}$ such that, when each vertex is assigned the sum of all edges incident to it $mod2k$, where $k=max(p,q)$, the resulting vertex labels are distinct. In this paper we proved necessary and sufficient conditions for some path and cycle related graphs to be edge odd graceful such as: Friendship graphs, Wheel graph, Helm graph, Web graph, Double wheel graph, Gear graph, Fan graph, Double fan graph and Polar grid graph.

Keywords:

• Edge odd graceful labeling
• Friendship graph
• Wheel graph
• Double fan graph
• Polar grid graph

1 Introduction

The field of Graph Theory plays an important role in various areas of pure and applied sciences. Graph Labeling of a graph $G$ is an assignment of integers either to the vertices or edges or both subject to certain conditions. Graph labeling is a very powerful tool that eventually makes things in different fields very ease to be handled in mathematical way. Nowadays graph labeling has much attention from different brilliant researches in graph theory which has rigorous applications in many disciplines, e.g., communication networks, coding theory, optimal circuits layouts, astronomy, radar and graph decomposition problems. See [1–^[2]3].

We begin with simple, connected, finite, undirected graph $G=(V\left(G\right),E\left(G\right))$ with $p=\left|V\left(G\right)\right|$ and $q=\left|E\left(G\right)\right|$.

In 1967, Rosa [4] introduced a labeling of $G$ called $\beta$-valuation, later on Solomon W. Golomb [5] called as “graceful labeling” which is an injection $f$ from the set of vertices $V\left(G\right)$ to the set $\{0,1,2,\dots ,q\}$ such that when each edge $e=uv$ is assigned the label $|f\left(u\right)-f\left(v\right)|$, the resulting edge labels are distinct. A graph which admits a graceful labeling is called a graceful graph.

In 1991, Gnanajothi [6] introduced a labeling of $G$ called odd graceful labeling which is an injection $f$ from the set of vertices $V\left(G\right)$ to the set $\{0,1,2,\dots ,2q-1\}$ such that when each edge $e=uv$ is assigned the label $|f\left(u\right)-f\left(v\right)|$, the resulting edge labels are $\{1,3,\dots ,2q-1\}$. A graph which admits an odd graceful labeling is called an odd graceful graph.

In 1985, Lo [7] introduced a labeling of $G$ called edge graceful labeling, which is a bijection $f$ from the set of edges $E\left(G\right)$ to the set $\{1,2,\dots ,q\}$ such that the induced map $f^{\ast }$ from the set of vertices $V\left(G\right)$ to $\{0,1,2,\dots ,p-1\}$ given by $f^{\ast }\left(u\right)={\sum }_{uv\in E\left(G\right)}f\left(uv\right)\left(modp\right)$ is a bijection. A graph which admits edge graceful labeling is called an edge graceful graph.

In 2009, Solairaju and Chithra [8] introduced a labeling of $G$ called edge odd graceful labeling, which is a bijection $f$ from the set of edges $E\left(G\right)$ to the set $\{1,3,\dots ,2q-1\}$ such that the induced map $f^{\ast }$ from the set of vertices $V\left(G\right)$ to $\{0,1,2,\dots ,2q-1\}$ given by $f^{\ast }\left(u\right)={\sum }_{uv\in E\left(G\right)}f\left(uv\right)\left(mod2q\right)$ is a bijection. A graph which admits edge odd graceful labeling is called an edge odd graceful graph.

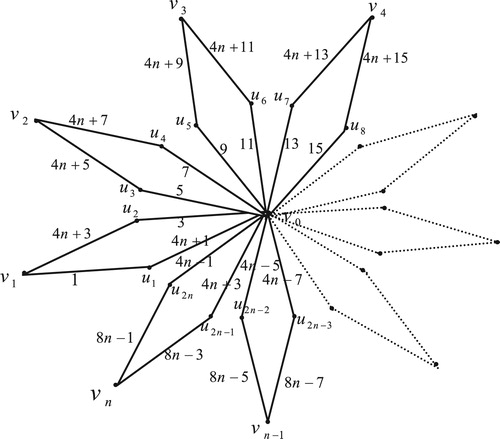
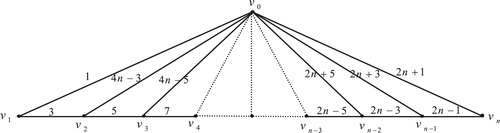
2 Edge odd graceful labeling of friendship graph $F{r}_n^{\left(3\right)}$

The friendship graph $F{r}_n^{\left(3\right)}$, is a planar undirected graph with $2n+1$ vertices and $3n$ edges constructed by joining $n$ copies of the cycle graph $C_3$ with a common vertex.

Theorem 1

The friendship graph $F_{r_n}^{\left(3\right)}$, is an edge odd graceful graph.

Proof

Using standard notation $p=\left|V\left(G\right)\right|=2n+1$, $q=\left|E\left(G\right)\right|=3n$ and $k=max(p,q)=3n$. There are three cases:

Case (1)$:n\equiv 0\left(mod3\right)$. Let the friendship graph $F_{r_n}^{\left(3\right)}$, be as in Fig. 1 and the triangles in it are $T_1,T_2,\dots ,T_n$. Name the center by $v_0$ and name the other two vertices of $T_i$ by $v_{2i-1},v_{2i},i=1,2,\dots ,n$. First label the outer edges, beginning from the base of triangle $T_1$ to the triangle $T_n$ by $1,3,\dots ,2n-1$, then label the inner edges incident to the center (hub) by $2n+1,2n+3,\dots ,6n-1$. Then we obtain the labels of vertices $v_i,i=1,2,\dots ,n$ as follows $:2n+2,2n+4;2n+8,2n+10;\dots ;2n-4,2n-2\left(mod6n\right).$

By rearranging this sequence, the pattern is clear. Now the label assigned to the vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [(2n+1)+(2n+3)+\cdots +(6n-1)]\equiv 4n^2\left(mod6n\right),$ since $n\equiv 0\left(mod3\right)$, we have $f^{\ast }\left(v_0\right)\equiv 0\left(mod6n\right)$. Therefore the friendship graph admits an edge odd graceful labeling in this case.

Case (2)$:n\equiv 1\left(mod3\right)$. Let the friendship graph $F_{r_n}^{\left(3\right)}$, be as in Fig. 2. First label the inner edges of the triangles $T_1,T_2,\dots ,T_n$ by $1,3,\dots ,4n-1$. Second label the outer edges beginning from the base of the triangle $T_1$ by $4n+1,4n+3,\dots ,6n-1$. The induced labels of vertices are as follows: $4n+2,4n+4;4n+8,4n+10;\dots ;10n-4\equiv 4n-4,10n-2\equiv 4n-2\left(mod6n\right)$. By rearranging this sequence, the pattern is clear . Now the label assigned to the vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv \frac{2n}{2}[1+(4n-1)]\equiv 4n^2\left(mod6n\right),$ since $n\equiv 1\left(mod3\right)$, we get $f^{\ast }\left(v_0\right)\equiv 4n\left(mod6n\right).$

Case (3)$:n\equiv 2\left(mod3\right)$. Let the friendship graph $F_{r_n}^{\left(3\right)}$, be as in Fig. 3. First label the inner edges of the triangles $T_1,T_2,\dots ,T_n$ by $3,5,\dots ,4n-1,4n+1$. Second label the outer edges beginning from the base of the triangle $T_1$ to the base of the triangle $T_{n-1}$ by $4n+3,4n+5,\dots ,6n-1$ and then label the base of the triangle $T_n$ by 1. Hence we have the labels of $v_i,i=1,2,\dots ,n$ are as follows: $4n,4n+2;4n+6,4n+8;\dots ;10n-6\equiv 4n-6,10n-4\equiv 4n-4\left(mod6n\right)$. By rearranging this sequence, the pattern is clear. Now the label assigned $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv \frac{2n}{2}[3+(4n+1)]\equiv (4n^2+4n)\left(mod6n\right),$ since $n\equiv 2\left(mod3\right)$, we get $f^{\ast }\left(v_0\right)\equiv 0\left(mod6n\right).$

Fig. 1 Friendship graph $F{r}_n^{\left(3\right)}$, $n\equiv 0\left(mod3\right)$.

Fig. 2 Friendship graph $F{r}_n^{\left(3\right)}$, $n\equiv 1\left(mod3\right)$.

Fig. 3 Friendship graph $F{r}_n^{\left(3\right)}$, $n\equiv 2\left(mod3\right)$.

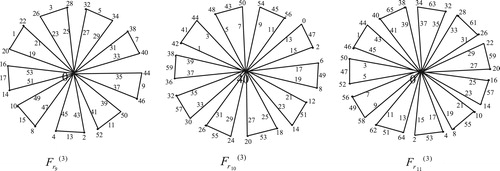
Illustration: The edge odd graceful labeling of the graphs $F_{r_9}^{\left(3\right)}$, $F_{r_{10}}^{\left(3\right)}$ and $F_{r_{11}}^{\left(3\right)}$ are shown in Fig. 4.

Fig. 4 The graphs $F{r}_9^{\left(3\right)}$, $F{r}_{10}^{\left(3\right)}$ and $F{r}_{11}^{\left(3\right)}$ are edge odd graceful graphs.

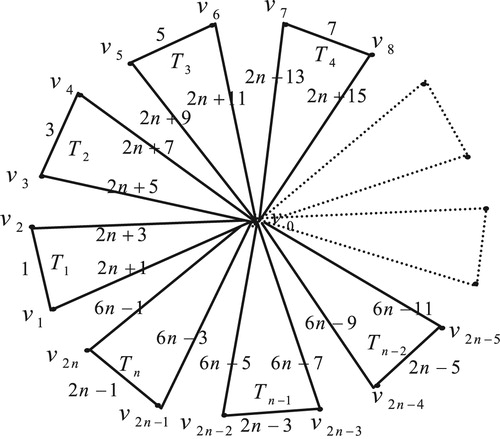
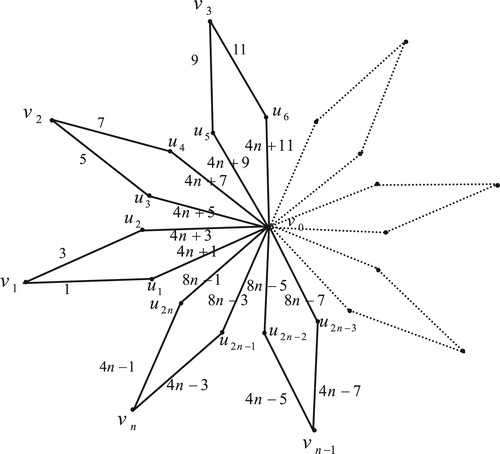
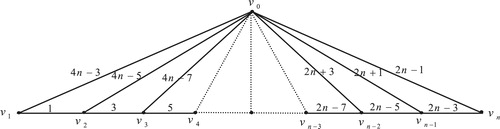
3 Edge odd graceful labeling of friendship graph $F{r}_n^{\left(4\right)}$

The friendship graph $F{r}_n^{\left(4\right)}$ is a planar undirected graph with $3n+1$ vertices and $4n$ edges constructed by joining $n$ copies of the cycle graph $C_4$ with a common vertex.

Theorem 2

The friendship graph $F_{r_n}^{\left(4\right)}$, is an edge odd graceful graph.

Proof

Here $p=\left|V\left(G\right)\right|=3n+1$, $q=\left|E\left(G\right)\right|=4n$ and $k=max(p,q)=4n$, there are two cases:

Case (1): When $n$ is odd. Let the friendship graph $F_{r_n}^{\left(4\right)}$, be as in Fig. 5. Label the inner edges $v_0{u}_2,v_0{u}_3,\dots ,v_0{u}_{2n},v_0{u}_1$ by $3,5,\dots ,4n+1$ and the outer edges $v_1{u}_1,v_1{u}_2;v_2{u}_3,v_2{u}_4;\dots ;v_n{u}_{2n-1},v_n{u}_{2n}$ by $1,4n+3;4n+5,4n+7;\dots ;8n-3,8n-1$. Thus we have the labels of vertices $v_i,i=1,2,\dots ,n$ are as follows: $4n+4,12,20,\dots ,8n-12,8n-4\left(mod8n\right)$, and the label of vertices $u_i,i=1,2,\dots ,2n$ are as follows $4n+2,4n+6,4n+10,\dots ,12n-2\equiv 4n-2\left(mod8n\right)$. Now the label assigned to the vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [3+5+\cdots +(4n+1)]\equiv (4n^2+4n)\left(mod8n\right)$, since $n$ is odd, we get $f^{\ast }\left(v_0\right)\equiv 0\left(mod8n\right)$.

Case (2): When $n$ is even. Let the friendship graph $F_{r_n}^{\left(4\right)}$, be as in Fig. 6. Label the outer edges $v_1{u}_1,v_1{u}_2;v_2{u}_3,v_2{u}_4;\dots ;v_n{u}_{2n-1},v_n{u}_{2n}$ by $1,3,5,\dots ,4n-1$ and the inner edges $v_0{u}_1,v_0{u}_2,\dots ,v_0{u}_{2n}$ by $4n+1,4n+3,\dots ,8n-1$. Thus we have the labels of vertices $v_i,i=1,2,\dots ,n$ are as follows $:4,12,20,\dots ,8n-12,8n-4\left(mod8n\right)$, and the labels of vertices $u_i,i=1,2,\dots ,2n$ are as follows $4n+2,4n+6,4n+10,\dots ,12n-2\equiv 4n-2\left(mod8n\right).$ Now the label assigned to the vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [(4n+1)+(4n+3)+\cdots +(8n-1)]\equiv 12n^2\left(mod8n\right),$ since $n$ is even, we have $f^{\ast }\left(v_0\right)\equiv 0\left(mod8n\right).$

Fig. 5 Friendship graph $F{r}_n^{\left(4\right)}$, $n$ is odd.

Fig. 6 Friendship graph $F{r}_n^{\left(4\right)}$, $n$ is even.

Illustration: The edge odd graceful labeling of graphs $F_{r_9}^{\left(4\right)}$ and $F_{r_{10}}^{\left(4\right)}$ are shown in Fig. 7.

Fig. 7 The graphs $F{r}_9^{\left(4\right)}$ and $F{r}_{10}^{\left(4\right)}$ are edge odd graceful graphs.

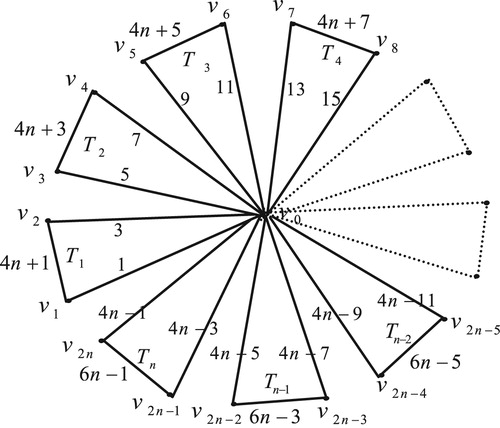
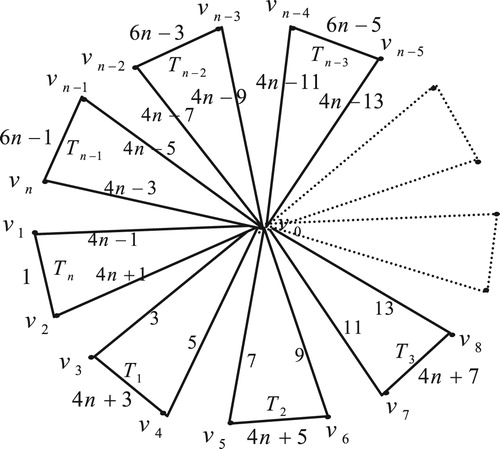
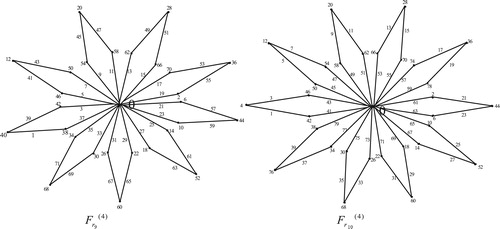
4 Edge odd graceful labeling of friendship graph $\bar{F}{r}_n^{\left(3\right)}$

The friendship graph $\bar{F}{r}_n^{\left(3\right)}$ is a planar undirected graph with $3n+1$ vertices and $5n$ edges constructed by joining $n$ copies of the fan graph $F_3$ with a common vertex.

Theorem 3

The friendship graph $\bar{F}{r}_n^{\left(3\right)}$, is an edge odd graceful graph.

Proof

Using standard notation $p=\left|V\left(G\right)\right|=3n+1$, $q=\left|E\left(G\right)\right|=5n$ and $k=max(p,q)=5n$.

Case (1): When $n\ne 30l-19$ or $n\ne 30l-5$ for $l=1,2,\dots ,n$. Let the friendship graph $\bar{F}{r}_n^{\left(3\right)}$, be as in Fig. 8.

Label the outer edges $u_1{v}_1,u_1{v}_2;u_2{v}_3,u_2{v}_4;\dots ;u_n{v}_{2n-1},u_n{v}_{2n}$ by $1,3,5,\dots ,4n-1$ and the inner edges $v_0{v}_i,i=1,2,\dots ,2n$ by $4n+1,4n+3,\dots ,8n-3,8n-1$, then label middle edges $v_0{u}_i,i=1,2,\dots ,n$ by $8n+1,8n+3,\dots ,10n-3,10n-1$. Thus we have the labels of vertices $v_i,i=1,2,\dots ,n$ are as follows $:4n+2,4n+6,4n+10,\dots ,12n-6\equiv 2n-6,12n-2\equiv 2n-2\left(mod10n\right)$ and the labels of vertices $u_i,i=1,2,\dots ,n$ are as follows $8n+5,11,17,\dots ,6n-7,6n-1\left(mod10n\right)$. Now the label assigned to central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [(4n+1)+(4n+3)+\cdots +(8n-1)+(8n+1)+\cdots +(10n-1)]\equiv 21n^2\equiv n^2\left(mod10n\right).$

Case (2): When $n=30l-19$ or $n=30l-5$ for $l=1,2,\dots ,n$. The proof is very similar as in case (1), only we interchange the labels of two middle edges $v_0{u}_{5l-3}$ and $v_0{u}_{5l-2}$ in case $n=30l-19$ and hence $f^{\ast }\left(v_0{u}_{5l-3}\right)\equiv 30l-21,f^{\ast }\left(v_0{u}_{5l-2}\right)\equiv 30l-11$, and in case $n=30l-5$, we interchange the labels of two middle edges $v_0{u}_{25l-4}$ and $v_0{u}_{25l-3}$ and hence $f^{\ast }\left(v_0{u}_{25l-4}\right)\equiv 150l-27,f^{\ast }\left(v_0{u}_{25l-3}\right)\equiv 150l-17$ to avoid repeated labels of vertices.

Fig. 8 Friendship graph $\bar{F}{r}_n^{\left(3\right)}$.

Illustration: The edge odd graceful labeling of the graphs $\bar{F}{r}_9^{\left(3\right)},\bar{F}{r}_{10}^{\left(3\right)},\bar{F}{r}_{11}^{\left(3\right)}$ and $\bar{F}{r}_{25}^{\left(3\right)}$ are shown in Fig. 9.

Fig. 9 The graphs $\bar{F}{r}_9^{\left(3\right)}$, $\bar{F}{r}_{10}^{\left(3\right)}$, $\bar{F}{r}_{11}^{\left(3\right)}$ and $\bar{F}{r}_{25}^{\left(3\right)}$ are edge odd graceful graphs.

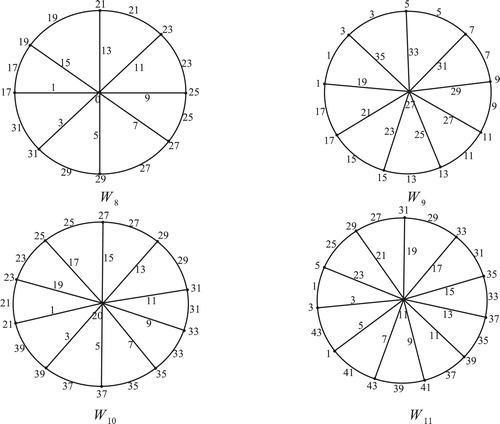
5 Edge odd graceful labeling of wheel graph $W_n$

Theorem 4

For $n>3$, the wheel graph $W_n=K_1+C_n$ is an edge odd graceful graph.

Proof

Using standard notation $p=\left|V\left(G\right)\right|=n+1$, $q=\left|E\left(G\right)\right|=2n$ and $k=max(p,q)=2n$, there are three cases:

Case (1): $n$ is even. Let the wheel graph be as in Fig. 10 with central vertex $v_0$. Move anticlockwise to label the interior edges $v_0{v}_1,v_0{v}_n,v_0{v}_{n-1},\dots ,v_0{v}_2$ by $1,3,5,\dots ,2n-1$, then move clockwise to label the cycle edges $v_1{v}_2,v_2{v}_3,v_3{v}_4,\dots ,v_{n-1}{v}_n,v_n{v}_1$ by $2n+1,2n+3,\dots ,4n-3,4n-1$.

Therefore the corresponding labels of vertices will be: $f^{\ast }\left(v_1\right)\equiv 2n+1,f^{\ast }\left(v_2\right)\equiv 2n+3,f^{\ast }\left(v_3\right)\equiv 2n+5,\dots ,f^{\ast }\left(v_{n-2}\right)\equiv 4n-5,f^{\ast }\left(v_{n-1}\right)\equiv 4n-3,f^{\ast }\left(v_n\right)\equiv 4n-1\left(mod4n\right).$The label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [1+3+\cdots +(2n-1)]\equiv n^2\left(mod4n\right)$. When $n\equiv 0\left(mod4\right)$, we have $f^{\ast }\left(v_0\right)\equiv 0\left(mod4n\right)$ and when $n\equiv 2\left(mod4\right)$, we have $f^{\ast }\left(v_0\right)\equiv 2n\left(mod4n\right)$.

Case (2)$:n\equiv 1\left(mod4\right)$. Let the wheel graph $W_n$ be as in Fig. 11. Move clockwise to label the cycle edges $v_1{v}_2,v_2{v}_3,v_3{v}_4,\dots ,v_{n-1}{v}_n,v_n{v}_1$ by $1,3,5,\dots ,2n-1$, then move anticlockwise to label the interior edges $v_0{v}_1,v_0{v}_n,v_0{v}_{n-1},\dots ,v_0{v}_2$ by $2n+1,2n+3,\dots ,4n-3,4n-1$. Therefore the corresponding labels of vertices will be $f^{\ast }\left(v_1\right)\equiv 1,f^{\ast }\left(v_2\right)\equiv 3,f^{\ast }\left(v_3\right)\equiv 5,\dots ,f^{\ast }\left(v_{n-2}\right)\equiv 2n-5,f^{\ast }\left(v_{n-1}\right)\equiv 2n-3,f^{\ast }\left(v_n\right)\equiv 2n-1\left(mod4n\right).$

Now the label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [(2n+1)+(2n+3)+\cdots +(4n-1)]\equiv 3n^{2}mod\left(4n\right)$, since $n\equiv 1\left(mod4\right)$, we have $f^{\ast }\left(v_0\right)\equiv 3n\left(mod4n\right)$.

Case (3): $n\equiv 3\left(mod4\right)$. Let the wheel graph $W_n$ be as in Fig. 12. Move anticlockwise to label the interior edges $v_0{v}_1,v_0{v}_n,v_0{v}_{n-1},\dots ,v_0{v}_2$ by $3,5,\dots ,2n+1$, then move clockwise to label the cycle edges $v_1{v}_2,v_2{v}_3,v_3{v}_4,\dots ,v_{n-1}{v}_n,v_n{v}_1$ by $1,2n+3,2n+5,\dots ,4n-3,4n-1$.

Therefore the corresponding labels of vertices will be : $f^{\ast }\left(v_1\right)\equiv 3,f^{\ast }\left(v_2\right)\equiv 5,f^{\ast }\left(v_3\right)\equiv 2n+7,f^{\ast }\left(v_4\right)\equiv 2n+9,\dots ,f^{\ast }\left(v_{n-2}\right)\equiv 4n-3,f^{\ast }\left(v_{n-1}\right)\equiv 4n-1,f^{\ast }\left(v_n\right)\equiv 1\left(mod4n\right).$Now the label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [3+5+\cdots +(2n+1)]\equiv (n^2+2n)\left(mod4n\right),$ since $n\equiv 3\left(mod4\right)$, we have $f^{\ast }\left(v_0\right)\equiv n\left(mod4n\right)$.

Fig. 10 Wheel graph $W_n$, $n$ is even.

Fig. 11 Wheel graph $W_n$, $n\equiv 1\left(mod4\right)$.

Fig. 12 Wheel graph $W_n$, $n\equiv 3\left(mod4\right)$.

Illustration: The edge odd graceful labeling of the wheel graphs $W_8,W_9,W_{10}$ and $W_{11}$ are shown in Fig. 13.

Fig. 13 The graphs $W_8$, $W_9$, $W_{10}$ and $W_{11}$ are edge odd graceful graphs.

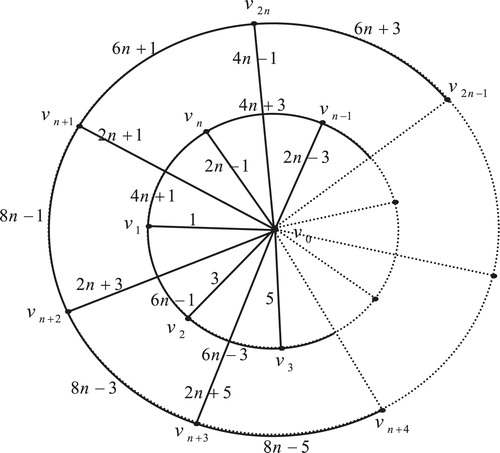
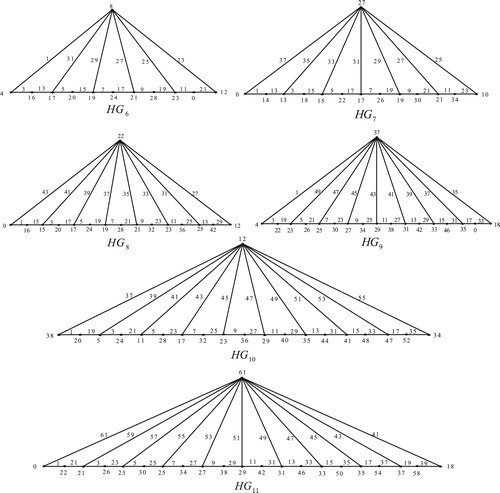
6 Edge odd graceful labeling of helm graph $H_n$

Theorem 5

The helm $H_n$ is an edge odd graceful graph.

Proof

Using standard notation $p=\left|V\left(G\right)\right|=2n+1$, $q=\left|E\left(G\right)\right|=3n$ and $k=max(p,q)=3n.$

Case (1): When $n$ is odd. Let the helm graph $H_n$ be as in Fig. 14 with central vertex $v_0$. First label the pendant edges $v_i{v}_{n+i},i=1,2,\dots ,n$ by $1,3,5,\dots ,2n-1$. Second label the interior edges $v_0{v}_{n+i},i=1,2,\dots ,n$ by $2n+1,2n+3,\dots ,4n-3,4n-1$, then label the cycle edges $v_1{v}_2,v_2{v}_3,v_3{v}_4,\dots ,v_{n-1}{v}_n,v_n{v}_1$ by $4n+1,4n+3,\dots ,6n-3,6n-1$. Therefore the corresponding labels of vertices will be $f^{\ast }\left(v_1\right)\equiv 2,f^{\ast }\left(v_2\right)\equiv 4n+10,f^{\ast }\left(v_3\right)\equiv 4n+18,\dots ,f^{\ast }\left(v_{n-2}\right)\equiv 6n-22,f^{\ast }\left(v_{n-1}\right)\equiv 6n-14,f^{\ast }\left(v_n\right)\equiv 6n-6\left(mod6n\right),f^{\ast }\left(v_{n+1}\right)\equiv 1,f^{\ast }\left(v_{n+2}\right)\equiv 3,f^{\ast }\left(v_{n+3}\right)\equiv 5,\dots ,f^{\ast }\left(v_{2n-1}\right)\equiv 2n-3,f^{\ast }\left(v_{2n}\right)\equiv (2n-1)\left(mod6n\right).$

Now the label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [(2n+1)+(2n+3)+\cdots +(4n-1)]\equiv 3n^2\left(mod6n\right)$, since $n$ is odd, we have $f^{\ast }\left(v_0\right)\equiv 3n\left(mod6n\right)$.

Case (2): When $n$ is even. Let the helm graph $H_n$ be as in Fig. 15 with central vertex $v_0$. First label the pendant edges $v_i{v}_{n+i},i=1,2,\dots ,n$ by $1,3,5,\dots ,2n-1$. Second move anticlockwise to label the interior edges $v_0{v}_{n+i},i=1,2,\dots ,n$ by $2n+1,2n+3,\dots ,4n-3,4n-1$, then label the cycle edges $v_1{v}_n,v_n{v}_{n-1},v_{n-1}{v}_{n-2},\dots ,v_3{v}_2,v_2{v}_1$ by $4n+1,4n+3,\dots ,6n-3,6n-1$.

Therefore the corresponding labels of vertices will be $f^{\ast }\left(v_1\right)\equiv 2,f^{\ast }\left(v_2\right)\equiv 4n-2,f^{\ast }\left(v_3\right)\equiv 4n-6,\dots ,$

$f^{\ast }\left(v_{n-2}\right)\equiv 14,f^{\ast }\left(v_{n-1}\right)\equiv 10,f^{\ast }\left(v_n\right)\equiv 6\left(mod6n\right)$. Rearranging this sequence, the pattern is clear.

The labels of the pendant vertices will be $f^{\ast }\left(v_{n+1}\right)\equiv 1,f^{\ast }\left(v_{n+2}\right)\equiv 3,f^{\ast }\left(v_{n+3}\right)\equiv 5,\dots ,f^{\ast }\left(v_{2n-1}\right)\equiv 2n-3$.

$f^{\ast }\left(v_{2n}\right)\equiv 2n-1\left(mod6n\right)$. The label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [(2n+1)+(2n+3)+\cdots .+(4n-1)]\equiv 3n^2\left(mod6n\right)$, since $n$ is even, we get$f^{\ast }\left(v_0\right)\equiv 0\left(mod6n\right)$.

Fig. 14 Helm graph $H_n$, $n$ is odd.

Fig. 15 Helm graph $H_n$, $n$ is even.

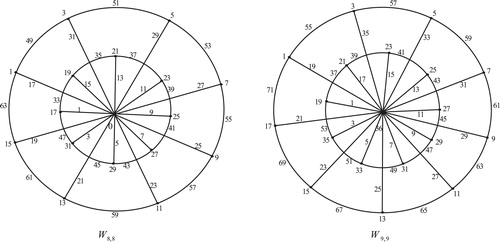
Illustration: The edge odd graceful labeling of the helm graphs $H_9$ and $H_{10}$ are shown in Fig. 16.

Fig. 16 The graphs $H_9$, and $H_{10}$ are edge odd graceful graphs.

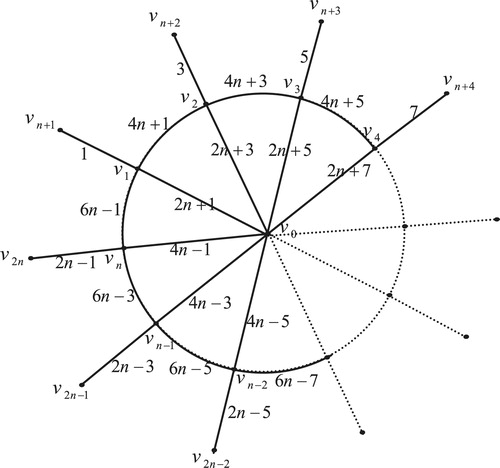
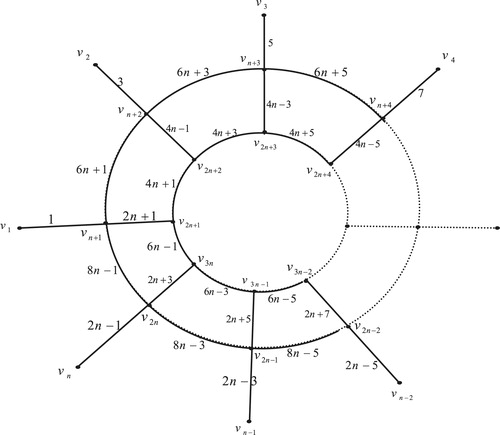
7 Edge odd graceful labeling of web graph $W{b}_n$

Theorem 6

The web graph $W{b}_n$, is an edge odd graceful graph.

Proof

Here $p=\left|V\left(G\right)\right|=3n$, $q=\left|E\left(G\right)\right|=4n$ and $k=max(p,q)=4n$. Let the web graph $W{b}_n$, be as in Fig. 17. First move clockwise to label the pendent edges $v_1{v}_{n+1},v_2{v}_{n+2},\dots ,v_{n-1}{v}_{2n-1},v_n{v}_{2n}$ by $1,3,\dots ,2n-3,2n-1$, then move anticlockwise to label the radial edges $v_{n+1}{v}_{2n+1},v_{2n}{v}_{3n},\dots ,v_{n+3}{v}_{2n+3},v_{n+2}{v}_{2n+2}$ by $2n+1,2n+3,\dots ,4n-3,4n-1$, then move clockwise to label the edges of inner cycle $v_{2n+1}{v}_{2n+2},v_{2n+2}{v}_{2n+3},\dots ,v_{3n-1}{v}_{3n},v_{3n}{v}_{2n+1}$ by $4n+1,4n+3,\dots ,6n-3,6n-1$. Finally label the edges of the external cycle $v_{n+1}{v}_{n+2},v_{n+2}{v}_{n+3},\dots ,v_{2n-1}{v}_{2n},v_{2n}{v}_{n+1}$ by $6n+1,6n+3,\dots ,8n-3,8n-1$.

Thus we have the labels of vertices are as follows: $f^{\ast }\left(v_i\right)\equiv 2i-1,f^{\ast }\left(v_{n+i}\right)\equiv 4i-2,f^{\ast }\left(v_{n+i}\right)\equiv 4n+2i-1\left(mod6n\right),i=1,2,\dots ,n.$

Fig. 17 Web graph $W{b}_n$.

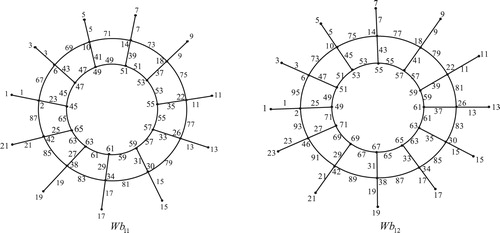
Illustration: The edge odd graceful labeling of the web graphs $W{b}_{11}$ and $W{b}_{12}$ are shown in Fig. 18.

Fig. 18 The graphs $W{b}_{11}$, and $W{b}_{12}$ are edge odd graceful labeling graphs.

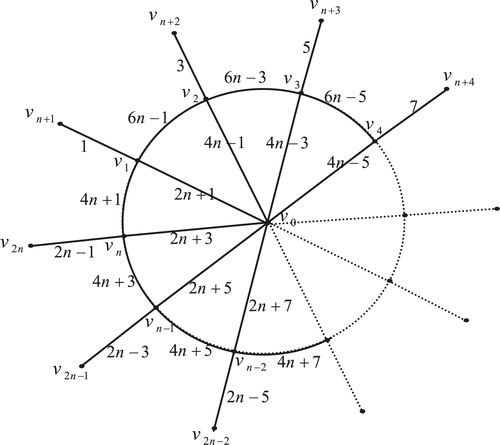
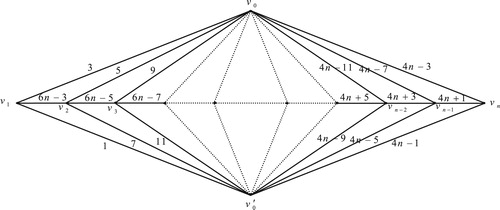
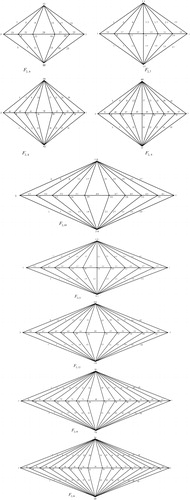
8 Edge odd graceful labeling of double wheel graph $W_{n,n}$

The double wheel graph $W_{n,n}$, consists of two cycles of $n$ vertices connected to a common hub.

Theorem 7

The double wheel graph $W_{n,n}$ is an edge odd graceful graph.

Proof

Using standard notation $p=\left|V\left(G\right)\right|=2n+1,q=\left|E\left(G\right)\right|=4n$ and $k=max(p,q)=4n$. Let the double wheel graph $W_{n,n}$ be as in Fig. 19 with central vertex $v_0$. First move anticlockwise to label the inner radial edges $v_0{v}_1,v_0{v}_2,\dots ,v_0{v}_n$ by $1,3,5,\dots ,2n-1$ and the outer radial edges $v_0{v}_{n+1},v_0{v}_{n+2},\dots ,v_0{v}_{2}n$ by $2n+1,2n+3,\dots ,4n-1$, then move clockwise to label the inner cycle edges $v_1{v}_n,v_n{v}_{n-1},\dots ,v_3{v}_2,v_2{v}_1$ by $4n+1,4n+3,\dots ,6n-3,6n-1$, and the outer cycle edges $v_{n+1}{v}_{2}n,v_{2}n{v}_{2n-1},\dots ,v_{n+3}{v}_{n+2},v_{n+2}{v}_{n+1}$ by $6n+1,6n+3,\dots ,8n-3,8n-1$.

Therefore the labels of vertices of the inner cycle will be $f^{\ast }\left(v_1\right)\equiv 2n+1,f^{\ast }\left(v_2\right)\equiv 4n-1,f^{\ast }\left(v_3\right)\equiv 4n-3,\dots ,f^{\ast }\left(v_{n-1}\right)\equiv 2n+5,f^{\ast }\left(v_n\right)\equiv 2n+3\left(mod8n\right),$ and the labels of vertices of the outer cycle will be $f^{\ast }\left(v_{n+1}\right)\equiv 1,f^{\ast }\left(v_{n+2}\right)\equiv 2n-1,f^{\ast }\left(v_{n+3}\right)\equiv 2n-3,\dots ,f^{\ast }\left(v_{2n-1}\right)\equiv 5,f^{\ast }\left(v_{2n}\right)\equiv 3\left(mod8n\right).$Rearranging these sequences, the pattern is clear.

Lastly the label assigned to the central vertex $V_0$ is given by $f^{\ast }\left(v_0\right)\equiv [1+3+\cdots +(2n-1)+((2n+1)+(2n+3)+\cdots +(4n-1))]\equiv 4n^2\left(mod8n\right),$therefore when is odd, we have $f^{\ast }\left(v_0\right)\equiv 4n\left(mod8n\right)$ and when is even, we get $f^{\ast }\left(v_0\right)\equiv 0\left(mod8n\right).$

Fig. 19 Double wheel graph $W_{n,n}$.

Illustration: The edge odd graceful labeling of the double wheel graphs $W_{8,8}$ and $W_{9,9}$ are shown in Fig. 20.

Fig. 20 The graphs $W_{8,8}$, and $W_{9,9}$ are edge odd graceful labeling graphs.

9 Edge odd graceful labeling of fan graph $F_n=K_1+P_n$

Theorem 8

The fan graph $F_n=K_1+P_n$ is an edge odd graceful graph.

Proof

Using standard notation $p=\left|V\left(G\right)\right|=n+1,q=\left|E\left(G\right)\right|=2n-1$ and $k=max(p,q)=2n-1$.

Case (1): $n\equiv 0\left(mod4\right)$ or $n\equiv 3\left(mod4\right)$. Let $v_0$ be the central vertex and $v_1,v_2,\dots ,v_n$ be the vertices of $P_n$ as in Fig. 21. Let $f:E\to \{1,3,\dots ,4n-3\}$ be defined by $f\left(v_{r-1}{v}_r\right)=2r-1,2\le r\le n$ and $f\left(v_0{v}_1\right)=1$, $f\left(v_0{v}_n\right)=2n+1$,$f\left(v_0{v}_{n-1}\right)=2n+3,\dots ,f\left(v_0{v}_2\right)=4n-3$. Therefore labels of vertices are as follows:$f^{\ast }\left(v_1\right)\equiv 4$, $f^{\ast }\left(v_2\right)\equiv 7$,$f^{\ast }\left(v_3\right)\equiv 9,\dots ,f^{\ast }\left(v_{n-1}\right)\equiv 2n+1$,$f^{\ast }\left(v_n\right)\equiv 2mod(4n-2)$.

The label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv 1+[(2n+1)+(2n+3)+\cdots +(4n-3)]\equiv 3n^2-4n+2\mathrm{mod}(4n-2).$When $n\equiv 0\left(\mathrm{mod}4\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{3}{2}n(mod4n-2)$ and when $n\equiv 3\left(mod4\right)$, we have thus$f^{\ast }\left(v_0\right)\equiv \frac{1}{2}(5n-1)(mod4n-2)$.

Case (2): $n\equiv 1\left(\mathrm{mod}4\right)$ or $n\equiv 2\left(\mathrm{mod}4\right)$. Let $f:E\to \{1,3,\dots ,4n-3\}$ be defined as in Fig. 22 by $f\left(v_{r-1}{v}_r\right)=2r-3,2\le r\le n$ and $f\left(v_0{v}_n\right)=2n-1$, $f\left(v_0{v}_{n-1}\right)=2n+1,\dots ,f\left(v_0{v}_3\right)=4n-7,f\left(v_0{v}_2\right)=4n-5,f\left(v_0{v}_1\right)=4n-3$.

Therefore labels of vertices are as follows: $f^{\ast }\left(v_1\right)\equiv 0$, $f^{\ast }\left(v_2\right)\equiv 1$,$f^{\ast }\left(v_3\right)\equiv 3,\dots ,f^{\ast }\left(v_{n-1}\right)\equiv 2n-5$,$f^{\ast }\left(v_n\right)\equiv (4n-4)mod(4n-2)$. The label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [(2n-1)+(2n+1)+\cdots +(4n-3)]\equiv (3n^2-2n)\mathrm{mod}(4n-2)$. When $n\equiv 1\left(mod4\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{2}(5n-3)(mod4n-2)$ and when $n\equiv 2\left(mod4\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{2}(3n-2)(mod4n-2)$.

Fig. 21 Fan graph $F_n$, $n\equiv 0\left(mod4\right)$ or $n\equiv 3\left(mod4\right)$.

Fig. 22 Fan graph $F_n$, $n\equiv 1\left(mod4\right)$ or $n\equiv 2\left(mod4\right)$.

Illustration: The edge odd graceful labeling of the fan graphs$F_8$, $F_9$, $F_{10}$ and $F_{11}$ are shown in Fig. 23.

Fig. 23 The graphs $F_8$, $F_9$, $F_{10}$ and $F_{11}$ are edge odd graceful graphs.

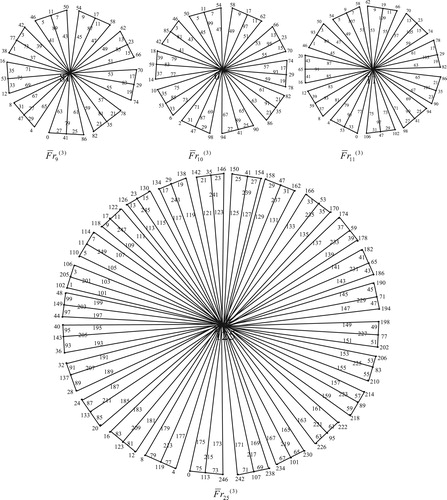
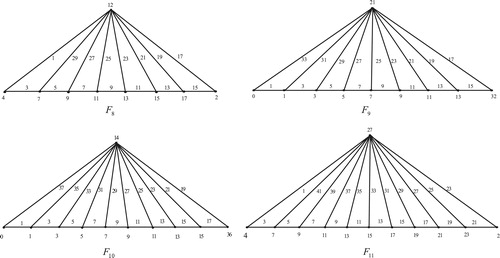
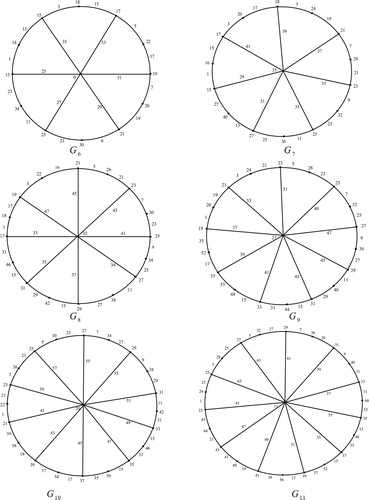
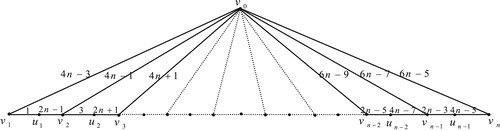
10 Edge odd graceful labeling of gear graph $G_n$

The Gear graph $G_n$, is the graph obtained from the wheel $W_n$ by inserting a vertex between any two adjacent vertices in its cycle $C_n$.

Theorem 9

The gear graph $G_n$ is an edge odd graceful graph.

Proof

Using standard notation $p=\left|V\left(G\right)\right|=2n+1,q=\left|E\left(G\right)\right|=3n$ and $k=max(p,q)=3n$. Let $f:E\to \{1,3,\dots ,6n-1\}$ be defined as in Fig. 24 by $f\left(v_r{u}_r\right)=2r-1$, $f\left(u_r{v}_{r+1}\right)=2n+2r-1,1\le r\le n$, and $f\left(v_0{v}_1\right)=4n+1$,$f\left(v_0{v}_n\right)=4n+3$, $f\left(v_0{v}_{n-1}\right)=4n+5,\dots ,f\left(v_0{v}_3\right)=6n-3,f\left(v_0{v}_2\right)=6n-1$.

Therefore labels of vertices are as follows: $f^{\ast }\left(v_1\right)\equiv 2n+1,f^{\ast }\left(v_2\right)\equiv 2n+3,f^{\ast }\left(v_3\right)\equiv 2n+5,\dots ,f^{\ast }\left(v_{n-1}\right)\equiv 4n-3,f^{\ast }\left(v_n\right)\equiv 4n-1\left(mod6n\right),f^{\ast }\left(u_1\right)\equiv 2n+2,f^{\ast }\left(u_2\right)\equiv 2n+6,f^{\ast }\left(u_3\right)\equiv 2n+10,\dots ,f^{\ast }\left(u_{n-1}\right)\equiv 6n-6,f^{\ast }\left(u_n\right)\equiv 6n-2\left(mod6n\right).$The label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [(4n+1)+(4n+3)+\cdots +(6n-1)]\equiv 5n^2\left(mod6n\right).$

(i)	When $n\equiv 0\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv 0\left(mod6n\right)$.

(ii)	When $n\equiv 1\left(mod6\right)$, we have$f^{\ast }\left(v_0\right)\equiv 5n\left(mod6n\right)$.

(iii)

When $n\equiv 2\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv 4n\left(mod6n\right)$.

(iv)	When $n\equiv 3\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv 3n\left(mod6n\right)$.

(v)	When $n\equiv 4\left(mod6\right)$, we have$f^{\ast }\left(v_0\right)\equiv 2n\left(mod6n\right)$.

(vi)	When $n\equiv 5\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv n\left(mod6n\right)$.

Fig. 24 Gear graph $G_n$.

Illustration: The edge odd graceful labeling of the gear graphs $G_6$, $G_7$, $G_8$, $G_9$, $G_{10}$ and $G_{11}$ are shown in Fig. 25.

Fig. 25 The graphs $G_6$, $G_7$, $G_8$, $G_9$, $G_{10}$ and $G_{11}$ are edge odd graceful graphs.

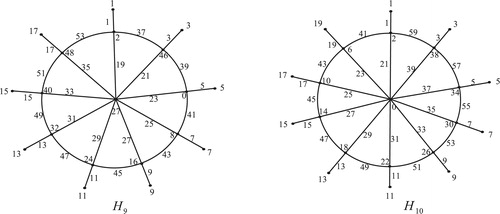
11 Edge odd graceful labeling of half gear graph $H{G}_n$

The half gear graph $H{G}_n$, is the graph obtained from the fan graph $F_n$ by inserting a vertex between any two adjacent vertices in its path $P_n$.

Theorem 10

The half gear graph $H{G}_n$ is an edge odd graceful graph.

Proof

Using standard notation $p=\left|V\left(G\right)\right|=2n,q=\left|E\left(G\right)\right|=3n-2$ and $k=max(p,q)=3n-2$.

Case (1): $n\equiv 0\left(\mathrm{mod}6\right)$ or $n\equiv 3\left(\mathrm{mod}6\right)$. Let $f:E\to \{1,3,\dots ,6n-5\}$ be defined as in Fig. 26. By $f\left(v_r{u}_r\right)=2r+1,f\left(u_r{v}_{r+1}\right)=2n+2r-1,1\le r\le n-1$, and $f\left(v_0{v}_n\right)=4n-1$, $f\left(v_0{v}_{n-1}\right)=4n+1$, $f\left(v_0{v}_{n-2}\right)=4n+3,\dots ,f\left(v_0{v}_3\right)=6n-7,f\left(v_0{v}_2\right)=6n-5,f\left(v_0{v}_1\right)=1$.

Therefore labels of vertices are as follows: $f^{\ast }\left(v_1\right)\equiv 4,f^{\ast }\left(v_2\right)\equiv 2n+5,f^{\ast }\left(v_3\right)\equiv 2n+7,\dots ,f^{\ast }\left(v_{n-1}\right)\equiv 4n-1$, $f^{\ast }\left(v_n\right)\equiv 2nmod(6n-4),f^{\ast }\left(u_1\right)\equiv 2n+4,f^{\ast }\left(u_2\right)\equiv 2n+8,f^{\ast }\left(u_3\right)\equiv 2n+12,\dots ,f^{\ast }\left(u_{n-2}\right)\equiv 6n-8,f^{\ast }\left(u_{n-1}\right)\equiv 6n-4\equiv 0mod(6n-4)$. The label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [1+(4n-1)+(4n+1)+\dots +(6n-5)]\equiv (5n^2-8n+4)mod(6n-4).$

(i)	When $n\equiv 0\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{4}{3}(mod6n-4)$.

(ii)	When $n\equiv 3\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(13n-6)(mod6n-4)$.

Case (2): $n\equiv 1\left(mod6\right)$ or $n\equiv 5\left(mod6\right)$. Let $f:E\to \{1,3,\dots ,6n-5\}$ be defined as in Fig. 27. By $f\left(v_r{u}_r\right)=2r-1,f\left(u_r{v}_{r+1}\right)=2n+2r-1,1\le r\le n-1$, and $f\left(v_0{v}_n\right)=4n-3$, $f\left(v_0{v}_{n-1}\right)=4n-1$, $f\left(v_0{v}_{n-2}\right)=4n+1,\dots ,f\left(v_0{v}_3\right)=6n-9,f\left(v_0{v}_2\right)=6n-7,f\left(v_0{v}_1\right)=6n-5$.

Therefore labels of vertices are as follows: $f^{\ast }\left(v_1\right)\equiv 0,f^{\ast }\left(v_2\right)\equiv 2n-1,f^{\ast }\left(v_3\right)\equiv 2n+1,\dots ,f^{\ast }\left(v_{n-1}\right)\equiv 4n-7,f^{\ast }\left(v_n\right)\equiv 2n-4mod(6n-4),f^{\ast }\left(u_1\right)\equiv 2n,f^{\ast }\left(u_2\right)\equiv 2n+4,f^{\ast }\left(u_3\right)\equiv 2n+8,\dots ,f^{\ast }\left(u_{n-2}\right)\equiv 6n-12,f^{\ast }\left(u_{n-1}\right)\equiv 6n-8mod(6n-4).$The label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [(4n-3)+(4n-1)+\cdots +(6n-5)]\equiv 5n^2-4nmod(6n-4).$

(i)	When $n\equiv 1\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(13n-10)(mod6n-4)$.

(ii)	When $n\equiv 5\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(n-2)(mod6n-4)$.

Case (3): $n\equiv 2\left(mod6\right)$. Let $f:E\to \{1,3,\dots ,6n-5\}$ be defined as in Fig. 28. By $f\left(v_r{u}_r\right)=2r-1,1\le r\le n-1$, $f\left(u_r{v}_{r+1}\right)=2n+2r-3,1\le r\le n-2$ and $f\left(u_{n-1}{v}_n\right)=4n-3$, $f\left(v_0{v}_n\right)=4n-5$, $f\left(v_0{v}_{n-1}\right)=4n-1$, $f\left(v_0{v}_{n-2}\right)=4n+1$, $f\left(v_0{v}_{n-3}\right)=4n+3,\dots ,f\left(v_0{v}_3\right)=6n-9$, $f\left(v_0{v}_2\right)=6n-7$, $f\left(v_0{v}_1\right)=6n-5$.

Therefore labels of vertices are as follows $f^{\ast }\left(v_1\right)\equiv 0,f^{\ast }\left(v_2\right)\equiv 2n-1,f^{\ast }\left(v_3\right)\equiv 2n+1,\dots ,f^{\ast }\left(v_{n-1}\right)\equiv 4n-7,f^{\ast }\left(v_n\right)\equiv 2n-4mod(6n-4),f^{\ast }\left(u_1\right)\equiv 2n,f^{\ast }\left(u_2\right)\equiv 2n+4,f^{\ast }\left(u_3\right)\equiv 2n+8,\dots ,f^{\ast }\left(u_{n-2}\right)\equiv 6n-12,f^{\ast }\left(u_{n-1}\right)\equiv 6n-6mod(6n-4).$The label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv (4n-5)+[(4n-1)+(4n+1)+\dots +(6n-5)]\equiv 5n^2-4n-2mod(6n-4).$

Since $n\equiv 2\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{2}{3}(5n-7)(mod6n-4)$.

Case (4): $n\equiv 4\left(mod6\right)$. Let $f:E\to \{1,3,\dots ,6n-5\}$ be defined as in Fig. 29 by $f\left(v_r{u}_r\right)=2r-1$, $f\left(u_r{v}_{r+1}\right)=2n+2r-3,1\le r\le n-1$ and $f\left(v_0{v}_1\right)=4n-3$, $f\left(v_0{v}_2\right)=4n-3$, $f\left(v_0{v}_2\right)=4n-1,\dots ,f\left(v_0{v}_{n-2}\right)=6n-9$, $f\left(v_0{v}_{n-1}\right)=6n-7$, $f\left(v_0{v}_n\right)=6n-5$.

Therefore labels of vertices are as follows: $f^{\ast }\left(v_1\right)\equiv 4n-2,f^{\ast }\left(v_2\right)\equiv 5,f^{\ast }\left(v_3\right)\equiv 11,\dots ,f^{\ast }\left(v_{n-1}\right)\equiv 6n-13,f^{\ast }\left(v_n\right)\equiv 4n-6mod(6n-4),f^{\ast }\left(u_1\right)\equiv 2n,f^{\ast }\left(u_2\right)\equiv 2n+4,f^{\ast }\left(u_3\right)\equiv 2n+8,\dots ,f^{\ast }\left(u_{n-2}\right)\equiv 6n-12,f^{\ast }\left(u_{n-1}\right)\equiv 6n-8mod(6n-4).$The label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [(4n-3)+(4n-1)+\cdots +(6n-5)]\equiv 5n^2-4nmod(6n-4)$. Since $n\equiv 4\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{4}{3}(n-1)(mod6n-4)$.

Fig. 26 Half gear graph $H{G}_n$, $n\equiv 0\left(mod6\right)$ or $n\equiv 3\left(mod6\right)$.

Fig. 27 Half gear graph $H{G}_n$, $n\equiv 1\left(mod6\right)$ or $n\equiv 5\left(mod6\right)$.

Fig. 28 Half gear graph $H{G}_n$, $n\equiv 2\left(mod6\right)$.

Fig. 29 Half gear graph $H{G}_n$, $n\equiv 9\left(mod6\right)$.

Illustration: The edge odd graceful labeling of the half gear graphs $H{G}_6$, $H{G}_7$, $H{G}_8$, $H{G}_9$, $H{G}_{10}$ and $H{G}_{11}$ are shown in Fig. 30.

Fig. 30 $H{G}_6$, $H{G}_7$, $H{G}_8$, $H{G}_9$, $H{G}_{10}$ and $H{G}_{11}$ are edge odd graceful labeling graphs.

12 Edge odd graceful labeling of double fan graph

Theorem 11

The double fan graph $F_{2,n}={\bar{K}}_2+p_n$, is an edge odd graceful graph.

Proof

Using standard notation $p=\left|V\left(G\right)\right|=n+2,q=\left|E\left(G\right)\right|=3n-1$ and $k=max(p,q)=3n-1$.

Case (1): $n$ is odd or $n\equiv 2\left(mod12\right)$ or $n\equiv 4\left(mod12\right)$ or $n\equiv 6\left(mod12\right)$. Let $f:E\to \{1,3,\dots 6n-3\}$ be defined as in Fig. 31. By $f\left(v_0{v}_r\right)=4r-3,f\left(v_0^{\prime }{v}_r\right)=4r-1,1\le r\le n,f\left(v_r{v}_{r+1}\right)=6n-2r-1,1\le r\le n-1.$

Therefore labels of vertices are as follows $f^{\ast }\left(v_1\right)\equiv 3,f^{\ast }\left(v_2\right)\equiv 8,f^{\ast }\left(v_3\right)\equiv 12,\dots f^{\ast }\left(v_{n-1}\right)\equiv 4n-4,f^{\ast }\left(v_n\right)\equiv 1mod(6n-2)$. The label assigned to the central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv [1+5+\cdots +(4n-3)]\equiv 2n^2-nmod(6n-2).$

(i)	When $n\equiv 1\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(5n-2)(mod6n-2).$

(ii)	When $n\equiv 3\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(17n-6)(mod6n-2).$

(iii)

When $n\equiv 5\left(mod6\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(11n-4)(mod6n-2).$

(iv)	When $n\equiv 2\left(mod12\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(11n-4)(mod6n-2).$

(v)	When $n\equiv 4\left(mod12\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(5n-2)(mod6n-2).$

(vi)	When $n\equiv 6\left(mod12\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(17n-6)(mod6n-2).$

The label assigned to the central vertex $v_0^{\prime }$ is given by $f^{\ast }\left(v_0^{\prime }\right)\equiv [3+5+\dots +(4n-1)]\equiv 2n^2+nmod(6n-2).$

(i)	When $n\equiv 1\left(mod6\right)$, we have $f^{\ast }\left(v_0^{\prime }\right)\equiv \frac{1}{3}(11n-2)(mod6n-2).$

(ii)	When $n\equiv 3\left(mod6\right)$, we have $f^{\ast }\left(v_0^{\prime }\right)\equiv \frac{5}{3}n(mod6n-2).$

(iii)

When $n\equiv 5\left(mod6\right)$, we have $f^{\ast }\left(v_0^{\prime }\right)\equiv \frac{1}{3}(17n-4)(mod6n-2).$

(iv)	When $n\equiv 2\left(mod12\right)$, we have $f^{\ast }\left(v_0^{\prime }\right)\equiv \frac{1}{3}(17n-4)(mod6n-2).$

(v)	When $n\equiv 4\left(mod12\right)$, we have $f^{\ast }\left(v_0^{\prime }\right)\equiv \frac{1}{3}(11n-2)(mod6n-2).$

(vi)	When $n\equiv 6\left(mod12\right)$, we have $f^{\ast }\left(v_0^{\prime }\right)\equiv \frac{5}{3}n(mod6n-2).$

Case (2): $n\equiv 0\left(mod12\right)$ or $n\equiv 8\left(mod12\right)$ or $n\equiv 10\left(mod12\right)$. Let $f:E\to \{1,3,\dots 6n-3\}$ be defined as in Fig. 32 by $f\left(v_0{v}_1\right)=3,f\left(v_0^{\prime }{v}_1\right)=1,f\left(v_0{v}_2\right)=4r-3,f\left(v_0^{\prime }{v}_r\right)=4r-1,1\le r\le n,f\left(v_r{v}_{r+1}\right)=6n-2r-1,1\le r\le n-1$. Therefore labels of vertices are as follows: $f^{\ast }\left(v_1\right)\equiv 3,f^{\ast }\left(v_2\right)\equiv 8,f^{\ast }\left(v_3\right)\equiv 12,\dots f^{\ast }\left(v_{n-1}\right)\equiv 4n-4,f^{\ast }\left(v_n\right)\equiv 1mod(6n-2).$

The label assigned to the central vertex is given by $f^{\ast }\left(v_0\right)\equiv 3+[5+\dots +(4n-3)]\equiv 2n^2-n+2mod(6n-2).$

(i)	When $n\equiv 0\left(mod12\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{17}{3}n(mod6n-2).$

(ii)	When $n\equiv 8\left(mod12\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(11n+2)(mod6n-2).$

(iii)

When $n\equiv 10\left(mod12\right)$, we have $f^{\ast }\left(v_0\right)\equiv \frac{1}{3}(5n+4)(mod6n-2).$

The label assigned to the central vertex is given by $f^{\ast }\left(v_0^{\prime }\right)\equiv [1+(7+11+\dots +(4n-1))]\equiv 2n^2-n+2mod(6n-2).$

(i)	When $n\equiv 0\left(mod12\right)$, we have $f^{\ast }\left(v_0^{\prime }\right)\equiv \frac{1}{3}(5n-2)(mod6n-2).$

(ii)	When $n\equiv 8\left(mod12\right)$, we have $f^{\ast }\left(v_0^{\prime }\right)\equiv \frac{1}{3}(17n-10)(mod6n-2).$

(iii)

When $n\equiv 10\left(mod12\right)$, we have $f^{\ast }\left(v_0^{\prime }\right)\equiv \frac{1}{3}(11n-8)(mod6n-2).$

Fig. 31 Double fan graph $F_{2,n}$, $n$ is odd or $n\equiv 2\left(mod12\right)$ or $n\equiv 4\left(mod12\right)$ or $n\equiv 6\left(mod12\right)$.

Fig. 32 Double fan graph $F_{2,n}$, $n\equiv 0\left(mod12\right)$ or $n\equiv 8\left(mod12\right)$ or $n\equiv 10\left(mod12\right)$.

Illustration: The edge odd graceful labeling of the double fan graphs $F_{2,6},F_{2,7},F_{2,8},F_{2,9},F_{2,10},F_{2,11},F_{2,12},F_{2,14},$ and $F_{2,16}$ and are shown in Fig. 33.

Fig. 33 The graphs $F_{2,6}$, $F_{2,7}$, $F_{2,8}$, $F_{2,9}$, $F_{2,10}$, $F_{2,11}$, $F_{2,12}$, $F_{2,14}$ and $F_{2,16}$ are edge odd graceful graphs.

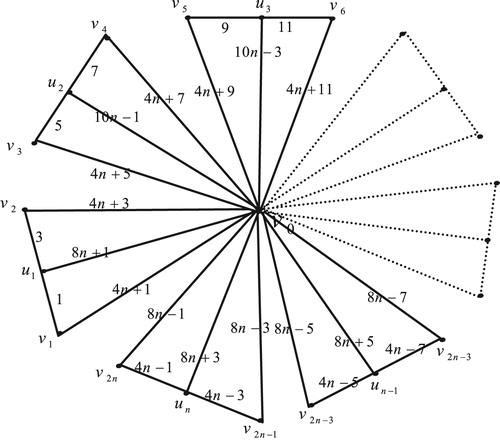
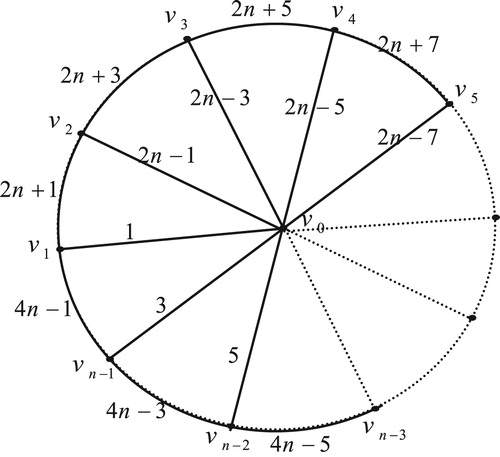
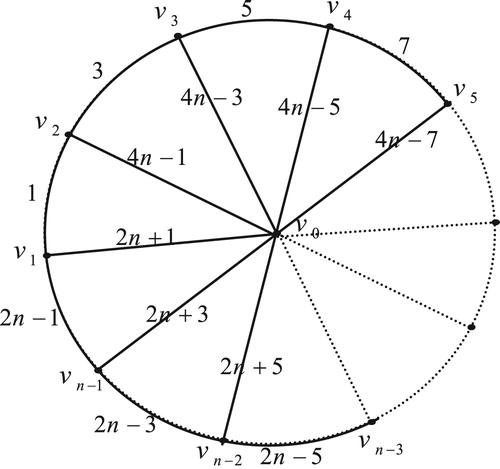
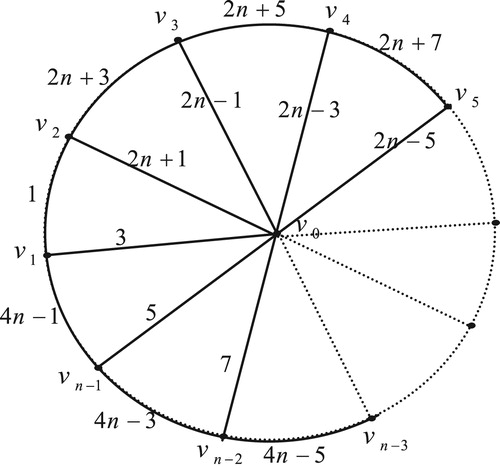
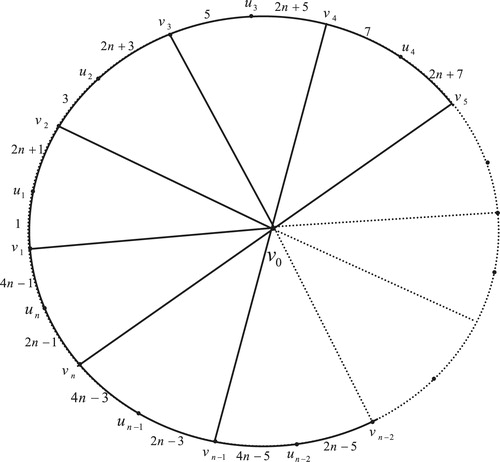
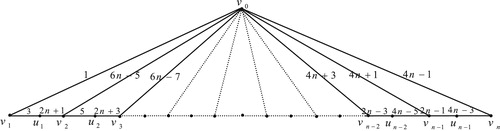
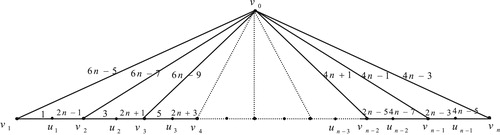
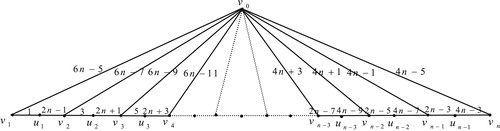
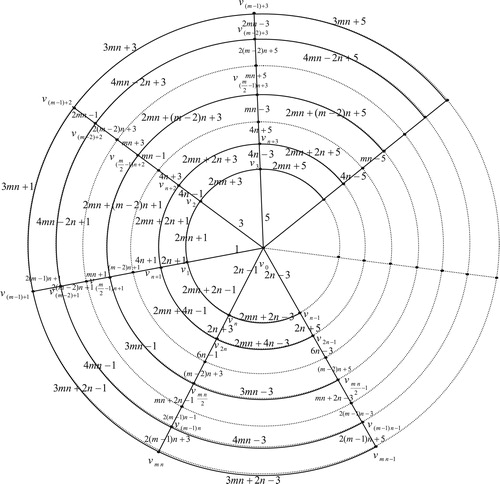
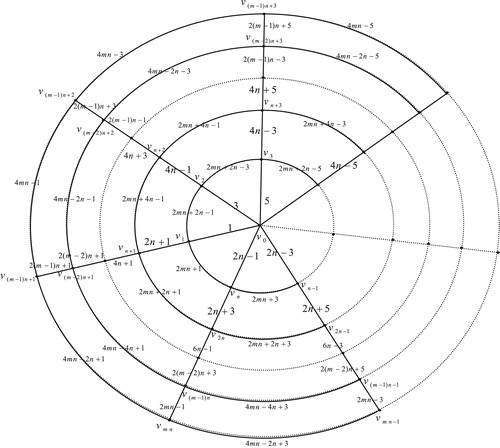
13 Edge odd graceful labeling of polar grid graph $P_{m,n}$

Theorem 12

The polar grid graph $P_{m,n}$, with radius $m$ and radii $n$ is an edge odd graceful graph.

Proof

Here $p=\left|V\left(G\right)\right|=mn+1,q=\left|E\left(G\right)\right|=2mn$, and $k=max(p,q)=2mn$, there are two cases:

Case (1): When $m$ is even. Let the polar grid graph $P_{m,n}$, be as in Fig. 34. First move clockwise to label the radii edges $v_0{v}_1,v_0{v}_2,v_0{v}_3\dots v_0{v}_n$ by $1,3,5,\dots ,2n-1$, then move anticlockwise to label the radii edges $v_1{v}_{n+1},v_n{v}_{2n},\dots ,v_3{v}_{n+3},v_2{v}_{n+2}$ by $2n+1,2n+3,\dots ,4n-3,4n-1$, then move clockwise to label the edges $v_{n+1}{v}_{2n+1},v_{n+2}{v}_{2n+2},\dots ,v_{2n-1}{v}_{3n-1},v_{2n}{v}_{3n}$ by $4n+1,4n+3\dots ,6n-3,6n-1$, and so on. Finally move anticlockwise to label the edges: $v_{(m-2)n+1}{v}_{(m-1)n+1},v_{(m-1)n}{v}_{mn},\dots ,v_{(m-2)n+2}{v}_{(m-1)n+1}$ by $2(m-1)n+1,2(m-1)n+3,\dots ,2mn-1$.

Now move clockwise to label the edge cycles as follows: First label the edges of inner cycle $v_1{v}_2,v_2{v}_3,\dots ,v_{n-1}{v}_n,v_n{v}_1$ by $2mn+1,2mn+3,\dots ,2mn+2n-3,2mn+2n-1$ and label the edges of second cycle $v_{n+1},v_{n+2},v_{n+3},\dots ,v_{2n+1}{v}_{2n},v_{2n}{v}_{n+1}$ by $2mn+2n+1,2mn+2n+3,\dots ,2mn+4n-3,2mn+4n_1$ and so on.

Then label the edges of the cycle of order $\frac{m}{2}$, $v_{(\frac{m}{2}-1)n+1}{v}_{(\frac{m}{2}-1)n+2},v_{(\frac{m}{2}-1)n+2}{v}_{(\frac{m}{2}-1)n+3},\dots ,v_{\frac{mn}{2}-2}{v}_{\frac{mn}{2}-1},v_{\frac{mn}{2}}{v}_{(\frac{m}{2}-1)n+1}$ by $2mn+(m-2)n+1,2mn+(m-2)n+3,\dots ,3mn-3,3mn-1$ , then label the edges of the cycle of order $m$, $v_{mn-n+1}{v}_{mn-n+2},v_{mn-n+2}{v}_{mn-n+3},\dots ,v_{mn-1}{v}_{mn},v_{mn}{v}_{mn-n+1}$ by $3mn+1,3mn+3,\dots ,3mn+2n-3,3mn+2n-1$. Then label the edges of order $\frac{m}{2}+1$, $v_{(\frac{m}{2}+1)n+1}{v}_{(\frac{m}{2}+1)n+2},v_{(\frac{m}{2}+1)n+2}{v}_{(\frac{m}{2}+1)n+3},\dots ,v_{\frac{mn}{2}+1}{v}_{(\frac{m}{2}+1)n+1}$. By $3mn+2n+1,3mn+2n+3,\dots ,3mn+4n-1$. Finally label the edges of the cycle of order $m-1,v_{mn-2n+1}{v}_{mn-2n+2},v_{mn-2n+2}{v}_{mn-2n+3},\dots ,v_{mn-n}{v}_{mn-2n+1}$, by $4mn-2n+1,4mn-2n+3,\dots ,4mn-3,4mn-1.$ Thus we have the labels of vertices $v_i,i=1,2,\dots ,mn$ are as follows: $f^{\ast }\left(v_1\right)\equiv 4n+2,f^{\ast }\left(v_2\right)\equiv 4n+6,f^{\ast }\left(v_3\right)\equiv 4n+10,\dots ,f^{\ast }\left(v_{n-1}\right)\equiv 8n-6,f^{\ast }\left(v_n\right)\equiv 8n-2\left(mod4mn\right);f^{\ast }\left(v_{n+1}\right)\equiv 12n+2,f^{\ast }\left(v_{n+2}\right)\equiv 12n+6,f^{\ast }\left(v_{n+3}\right)\equiv 12n+10,\dots ,f^{\ast }\left(v_{2n-1}\right)\equiv 16n-6,f^{\ast }\left(v_{2n}\right)\equiv 16n-2\left(mod4mn\right),\dots ,f^{\ast }\left(v_{(\frac{m}{2}-1)n+1}\right)\equiv 4mn-4n+2,f^{\ast }\left(v_{(\frac{m}{2}-1)n+2}\right)\equiv 4mn-4n+6,f^{\ast }\left(v_{(\frac{m}{2}-1)n+3}\right)\equiv 4mn-4n+10,\dots ,f^{\ast }\left(v_{(\frac{m}{2}-1)n}\right)\equiv 4mn-6,f^{\ast }\left(v_{\frac{mn}{2}}\right)\equiv 4mn-2\left(mod4mn\right);\dots ;f^{\ast }(v_{\frac{mn}{2}}+1)\equiv 8n+2,f^{\ast }(v_{\frac{mn}{2}}+2)\equiv 8n+6,f^{\ast }(v_{\frac{mn}{2}}+3)\equiv 8n+10,\dots ,f^{\ast }(v_{\frac{mn}{2}}+n)\equiv 12n-2;f^{\ast }\left(v_{(m-2)n+1}\right)\equiv 4mn-8n+2,f^{\ast }\left(v_{(m-2)n-1}\right)\equiv 4mn-8n+6,\dots ,f^{\ast }\left(v_{(m-1)n-1}\right)\equiv 4mn-4n-6,f^{\ast }\left(v_{(m-1)n}\right)\equiv 4mn-4n-2$. Now the label assigned to central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv \frac{n}{2}[1+2n-1]\equiv n^2\left(mod4mn\right).$

Case (2): When $m$ is odd. There are two subcases

(i)

When $n\equiv 3\left(mod4\right)$. Let the polar grid graph $P_{m,n}$, be as in Fig. 35. The label of radial edges is the same as when $n$ is even. Move anticlockwise to label the edges of inner cycle $v_1{v}_n,v_n{v}_{n-1},v_{n-1}{v}_{n-2},\dots ,v_3{v}_2,v_2{v}_1$, by, $2mn+1,2mn+3,2mn+5,\dots ,2mn+2n-3,2mn+2n-1$ the move the edges of second cycle $v_{n+1}{v}_{2n},v_{2n}{v}_{2n-1},\dots ,v_{n+3}{v}_{n+2},v_{n+2}{v}_{n+1}$ by $2mn+2n+1,2mn+2n+3,\dots ,2mn+4n-3,2mn+4n-1$ and so on.

Finally label the edges of the cycle of order $m,v_{mn-n+1}{v}_{mn},v_{mn}{v}_{mn-1},\dots ,v_{mn-n+3}{v}_{mn-n+2},v_{mn-n+2}{v}_{mn-n+1}$ by $4mn-2n+1,4mn-2n+3,\dots ,4mn-3,4mn-1$. Thus we have the labels of vertices $v_i,i=1,2,\dots ,mn$ are as follows: $f^{\ast }\left(v_1\right)\equiv 4n+2,f^{\ast }\left(v_n\right)\equiv 4n+6,f^{\ast }\left(v_{n-1}\right)\equiv 4n+10,\dots ,f^{\ast }\left(v_3\right)\equiv 8n-2\left(mod4mn\right),f^{\ast }\left(v_{n+1}\right)\equiv 12n+2,f^{\ast }\left(v_{2n}\right)\equiv 12n+6,f^{\ast }\left(v_{2n-1}\right)\equiv 12n+10,\dots ,f^{\ast }\left(v_{n+3}\right)\equiv 16n-6,f^{\ast }\left(v_{n+2}\right)\equiv 16n-2\left(mod4mn\right),\dots ,f^{\ast }\left(v_{(m-2n)+1}\right)\equiv 4mn-12n+2,f^{\ast }\left(v_{(m-1)n}\right)\equiv 4mn-12n+6,f^{\ast }\left(v_{(m-1)n-1}\right)\equiv 4mn-12n+10,\dots ,f^{\ast }\left(v_{(m-2)n+3}\right)\equiv 4mn-8n-6,f^{\ast }\left(v_{(m-2)n+2}\right)\equiv 4mn-8n-2;f^{\ast }\left(v_{(m-1)n+1}\right)\equiv 4mn-4n+1,f^{\ast }\left(v_{mn}\right)\equiv 2mn-4n+3,f^{\ast }\left(v_{(mn-1)}\right)\equiv 2mn-4n+5,\dots ,f^{\ast }\left(v_{(m-1_n+3)}\right)\equiv 2mn-2n-3,f^{\ast }\left(v_{(m-1)n+2}\right)\equiv 2mn-2n-1$.

Now the label assigned to central vertex $v_0$ is given by $f^{\ast }\left(v_0\right)\equiv \frac{n}{2}[1+2n-1]\equiv n^2\left(mod4mn\right).$

(ii)

When $n\equiv 3\left(mod4\right)$ and $m=n-2i,i\in N$. The proof is very similar as in subcase (i), only we interchange the labels of two radii edges $v_0{v}_1$ and $v_1{v}_{n+1}$ to avoid repeated labels of vertices. In this case $f^{\ast }\left(v_0\right)\equiv n(n+2),f^{\ast }\left(v_{n+1}\right)\equiv (10n+2)\left(mod4mn\right)$.

Fig. 34 Polar grid graph $P_{m,n}$, $m$ is even.

Fig. 35 Polar grid graph $P_{m,n}$, $m$ is odd.

Illustration : The edge odd graceful labelings of the polar grid graphs $P_{4,15},P_{5,13},P_{5,16},P_{6,12},$ and $P_{7,11}$ are shown in Fig. 36.

Fig. 36 The graphs $P_{4,15}$, $P_{5,13}$, $P_{5,16}$, $P_{6,12}$ and $P_{7,11}$ are edge odd graceful graphs.

Notes

Peer review under responsibility of Kalasalingam University.