?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
For any (finite simple) graph the secure domination number of
satisfies
. Here we find a secure-dominating set
in
such that
in all cases when
is a grid, and in the majority of cases when
is a cylindrical or toroidal grid. In all such cases,
satisfies the additional requirement that
is connected. We make note that the concept of secure-dominating sets considered in this paper is quite different from the other secure domination currently of interest.Footnote1
1 Introduction
All graphs will be finite and simple. The vertex and edge sets of a graph are denoted
and
, respectively. An edge joining vertices
and
may be denoted
or
. If
, the open neighbor set of
in
is
. If
is the only graph in the discussion, the subscript
may be omitted, in this notation. For instance, we define the closed neighborhood of
to be
. If
,
and
. A set
is
in
if and only if
. A dominating set
is called a perfect dominating set if every vertex in
has exactly one neighbor in
.
In an on
, in
, each vertex in
may expend its one unit of aggression by attacking one vertex of
to which it is adjacent (joined to by an edge of
). In a defense of
, each vertex of
may expend its one unit of defense by defending either itself or one of its neighbors in
. A defense of
thwarts or overcomes an attack on
if and only if each vertex of
has at least as many defenders as attackers.
is
in
if and only if for every attack on
there is a defense which thwarts that attack.
Suppose and
; that is,
has more potential attackers than potential defenders. If every vertex in
attacks one of its neighbors in
, then no matter how the defensive capabilities of
are allocated, at least one vertex of
will have more attackers than defenders. These observations disclose a necessary condition for security that turns out to be, in the fundamental theorem of security, sufficient.
Theorem 1.1
Brigham, Dutton, and Hedetniemi 2007; see also [Citation1]
Suppose is a graph. A set
is secure in
if and only if for any
,
.
A set is secure-dominating if it is both secure and dominating. As observed in [Citation2], if
is secure-dominating in
, then
; otherwise, if
, then
, and so
has more potential attackers than defenders. Therefore, if we define the secure-domination number of
,
, to be the minimum cardinality of a secure-dominating set in
, then
The interesting evidence from [Citation2] is that for a great many common graphs such as paths, most cycles, complete multipartite graphs, n-cubes, the Petersen graph, and many more, . The only exceptions to this statement on the list above are the cycles
on
vertices (
), for which
.
A is a Cartesian product
of non-trivial
paths; a cylindrical grid is a Cartesian product
of a non-trivial path with a cycle
; and a toroidal grid is a Cartesian product
of cycles
. We will show that if
is any of the first two types of grid, then
, and more: a secure-dominating set
can be found such that
and, in addition, the subgraph induced by
in
, usually denoted
, is connected.
In such a case we say that is a connected secure-dominating set. For arbitrary connected graphs
the minimum cardinality of a connected secure-dominating set is denoted
. Clearly,
. Our aim here is to show that equality holds throughout, in this last string of inequalities, when
is one of these blankety-blank grids. We have not achieved this aim for the toroidal grids, and perhaps it is not achievable. But
does hold for better than
of the toroidal grids, in a sense that will be clear.
For those interested in applications, we note that a connected secure-dominating set is a connected dominating set, which is also a connected hub set [Citation3], and all of these are of interest in street design, transportation, and network communication problems, which often involve grid graphs with mutations (holes, loops, other deformities). Surely, in this day and age, security is a desirable property for connected dominating and connected hub sets. It is shown in [Citation3] that every minimum connected dominating set has at most one vertex more than a minimum connected hub set. The study of connected secure hub sets is wide open, at present. Our results for connected secure dominating sets in grids may be compared with the results in [Citation4], on connected dominating sets in grids.
2 Results
Throughout, the vertices of or
will be
, along the path or around the cycle; the vertices of
or
will be
; the ordered pair
, a vertex of
or
or
, will be denoted
.
Theorem 2.1
If are integers, then
.
Proof
Since for all graphs
, it suffices in each case to find a connected secure dominating set
such that
.
Case 1: . Take
.
Case 2: . Take
.
In these first two cases, each vertex of has exactly one neighbor in
, so
is a perfect dominating set in
. A defensive strategy is easy: each
defends itself. This opens an interesting question that we will leave for others. Which graphs admit connected secure-dominating sets, which are also perfect dominating sets? In the cases to follow, and in the proofs of Theorems 2.2 and 2.3, it will be self-evident that the proposed connected secure-dominating sets are connected and dominating, but verifying security will be more difficult. Airtight proofs based on appeals to Theorem 1.1 can be provided, but these would be lengthy and unintuitive. We prefer an informal approach, in which a defense thwarting the various possible attacks is indicated informally, and it is left to the reader to verify that no clever attack can be found. The task will be simplified by the circumstance that most of the vertices of
will have a unique neighbor in
; we may as well assume that, in any attack, each of those vertices will attack its unique neighbor in
. Then the question is, What will the vertices in
that have a choice do, and can their attack be thwarted? To illustrate, consider
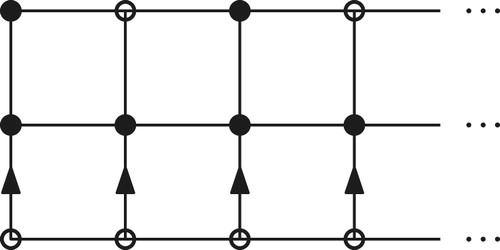
Case 3: . Take
. (See .)
The bottom row are all in
; each
will attack
. Each
,
even, has a choice of 3 vertices of
to attack, unless
is even and
, in which case the choice is two vertices.
To see that is secure, let us consider the first doubtful case,
, and some of 6 possible attacks. First, suppose that
attacks
. If
does not attack
then let
,
, and
defend themselves; we leave it to the reader to verify that
can then defend itself whether
attacks
or
. If, on the other hand
does attack
, so that
has 2 attackers,
and
, then obviously the only possible successful defense will start with
defending itself, and
and
defending
. This leads to
defending
defending
, and
defending
, and this defense defeats the attack.
In another attack, suppose that attacks
, which then has 2 attackers. The only possible way to save the day is for
to defend
, which is, of course, defending itself. Then if
is not attacking
, we simply let if
defend
, and we are back to a case in which the rest of the attack can be thwarted, regardless of what
does. On the other hand, if
attacks
then
must defend itself, and, as before,
defends
defends
, and
defends
.
We hope the reader, after working through these cases when , will agree that, not only is
secure for all values of
(the argument is less delicate when
is odd), but also that there is a relatively simple set of military-style, battlefield instructions for each vertex in
, telling the vertex
who to defend in each of a small number
of cases, defined by how many attackers each vertex in
has and also, for
, when
has only one attacker, whether or not
is defending itself, or being defended by
, or neither. It would be tedious to prove that such explicit battlefield instructions produce a successful defense, and we are not going to try, but we mention this because clearly such instructions bear on applications: a successful defense can be constructed by the troops by transmission of local intelligence (right-to-left along the columns of the grid, so that
can be apprised of what
has been instructed to do), without each soldier in
having to know anything about the attack around vertices of
a distance
in the grid from the soldiers.
By Cases 1–3, we may now assume that both and
are greater than 4.
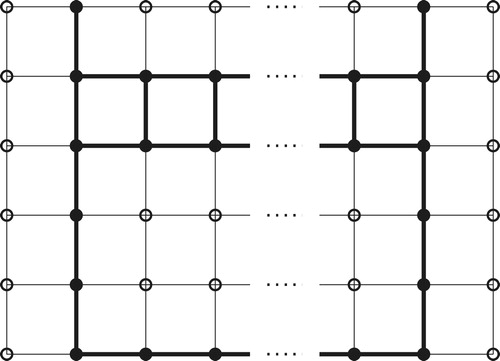
Case 4: and
: Take
.
We illustrate in , with and
, and
indicated by darkening
.
It is helpful to realize that for any values of ,
, the set
is obtainable by repeating the pattern in the first 4 rows of the
grid in each of the
blocks of 4 rows each into which the grid can be partitioned.
With this aid to understanding, it is clear that is connected and dominating, with
vertices. The security of
is much easier to see than the corresponding claim in Case 3; in the battlefield instructions to the vertices of
for defending against an attack, many (must, if
is large) vertices will be instructed to defend themselves, in all circumstances, and the others will have to defend a neighbor under only one local attack variation. For instance,
will each defend themselves unless and only unless
attacks
, giving
two attackers. When this happens,
will defend
and
(which has no attacker if
is attacking
) defends
.
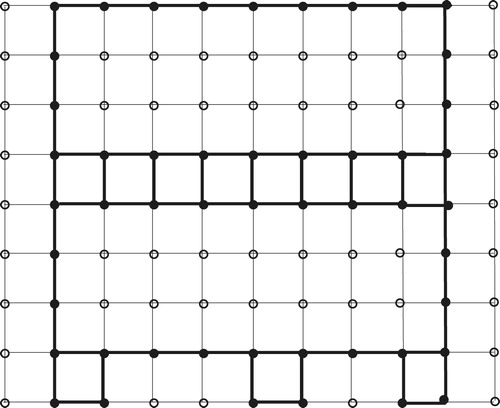
Case 5: : Take
.
This amounts to adding two rows to the pattern for that look like (with elements of
darkened):
We illustrate with , and
unspecified. (See .)
From Cases 1–5 we are left with the cases , both odd.
Case 6: ,
, odd: Take
, where
if
, and
if
. See .
Case 7: ,
, odd: Take
, where
is as in Case 6. See . □
Theorem 2.2
If and
are integers, then
except, possibly, in the cases
,
, when
, and
,
, when
.
Proof
Suppose that is secure and dominating in
and that, for each
if and only if
. It then follows that
is secure and dominating in
, which is obtained from
by adding the edges
; obviously
is dominating in the larger graph, and it is secure because each
has the same set of potential attackers in
as in
, and its neighbor set in
, in
, contains its neighbor set in
in
; that is, it has the same set of potential attackers and has lost no potential defenders in the transition from
to
.
Therefore the claim of Theorem 2.2 follows from the proof of Theorem 2.1 in all cases except, possibly, in the cases
| (i) |
| ||||
| (ii) |
| ||||
| (iii) |
| ||||
The reduction to these cases from the proof of Theorem 2.1 uses, of course, the obvious isomorphism of and
.
Since we are giving up on the cases under (iii), and
,
,
, we need only verify the claim of the theorem in cases (i), (ii), and
:
and
, (
), or
and
. For practical purposes it is worth noting that in case
the secure-dominating sets to be given are also secure-dominating in
, adding to the supply of minimum secure-dominating sets in plain grids. The new secure-dominating sets in case (ii), for
, are not dominating for
.
In the cases ,
even
, it turns out that the secure dominating set in
given in the proof Theorem 1, Case 3, is also secure and dominating in
, even though the variety of attacks to be thwarted has increased with the addition of the edges
. As in the proof of Theorem 2.1, we leave it to the reader to verify this claim, most usefully by providing battlefield instructions to the vertices of
for reacting to any attack. Anyone who found such instructions for the
case (n even) will find that they have not much changed, in fact, they will become simpler, in that instructions to the vertices
odd, will be pretty much the same, for different
.
For ,
, let
be as follows.
| (1) | If | ||||
| (2) | If | ||||
| (3) | If | ||||
| (4) | If | ||||
The cases ,
,
if
, divide into 2 subcases.
| (1) |
| ||||
| (2) |
| ||||
(See –.)
Theorem 2.3
Suppose that are integers. Let
. Then
except, possibly, in the following cases:
| (1) |
| ||||
| (2) |
| ||||
| (3) |
| ||||
| (4) |
| ||||
Proof
Let us say that a pair is
if and only if
. Obviously
is good if and only if
is good.
As at the beginning of the proof of Theorem 2.2, we observe that if is a secure-dominating set of vertices in
such that
if and only if
then
is also secure-dominating in
. Applying this observation to the secure-dominating sets in the proof of Theorem 2.2, some of which were imported from the proof of Theorem 2.1, we find that
is good in the following cases,
| (i) |
| ||||
| (ii) |
| ||||
| (iii) |
| ||||
Therefore, to finish the proof, it will suffice to show that the following pairs are
:
| (a) |
| ||||
| (b) |
| ||||
| (c) |
| ||||
| (d) |
| ||||
Here are the secure-dominating sets that show that is a good pair, in these cases.
| (a) |
| ||||
| (b) |
| ||||
| (c) |
| ||||
| (d) |
| ||||
Determining in the cases left open by Theorem 2.3 is a worthy problem. We remark that it is easy to see that
, for all
. In the other cases we can show that
, but feel that some clever person will soon surpass this estimate. □
Notes
Peer review under responsibility of Kalasalingam University.
1 The other sort of secure domination: A dominating set is secure dominating (in G) if and only if for every
there is some
such that
is dominating, in G.
References
- GarthIsaacPeterJohnsonCalebPetrieInteger and fractional security in graphsDiscrete Appl. Math.160201220602062
- PeterJohnsonCadaviousJonesSecure dominating sets in graphsV.R.KulliAdvances in Domination Theory II2013Vishwa International Publications19 ISBN 81-900205-6-0
- PeterJohnsonPeterSlaterMatthewWalshThe connected hub number and the connected domination numberNetworks582011171180
- EgbertMujuniConnected dominating set problem for hypercubes and grid graphiCASTOR J. Math. Sci.7220138189