Minimal 2-point set dominating sets of a graph

Peer review under responsibility of Kalasalingam University.

Abstract

A set $D\subseteq V\left(G\right)$ is a 2-point set dominating set (2-psd set) of a graph $G$ if for any subset $S\subseteq V-D$, there exists a non-empty subset $T\subseteq D$ containing at most two vertices such that the induced subgraph $〈S\cup T〉$ is connected. In this paper we characterize minimal 2-psd sets for a general graph. Based on the structure we examine 2-psd sets in a separable graph and discuss the criterion for a 2-psd set to be minimal.

Keywords:

• 2-Point set domination
• Point set domination
• Domination

1 Introduction

By a graph $G$ we mean a finite, undirected, connected and non-trivial graph with neither loops nor multiple edges. The order $\left|V\left(G\right)\right|$ and the size $\left|E\left(G\right)\right|$ of $G$ are denoted by $n$ and $m$ respectively. For graph theoretic terminology we refer to Harary [1] and West [2]. The open neighborhood $N\left(v\right)$ of any vertex $v$ in $G$ is $\{x:xv\in E\left(G\right)\}$ and closed neighborhood $N\left[v\right]$ of $v$ in $G$ is $N\left(v\right)\cup \left\{v\right\}$. For a set $S\subseteq V\left(G\right)$ the open (closed) neighborhood of $S$ in $G$ is $N\left(S\right)\left(N\left[S\right]\right)$ and is defined as $N\left(S\right)={\cup }_{v\in S}N\left(v\right)(N\left[S\right]={\cup }_{v\in S}N\left[v\right])$.

Definition 1.1

[3]

A set $D\subseteq V\left(G\right)$ is a dominating set of a graph $G$ if for every vertex $v$ in $V-D$, there exists a vertex $u\in D$ such that $v$ is adjacent to $u$. The domination number of $G$ is the minimum cardinality of a dominating set of $G$.

Definition 1.2

[4]

A set $D\subseteq V\left(G\right)$ is a set dominating set of a graph $G$ if for every set $S\subseteq V-D$, there exists a non-empty set $T\subseteq D$ such that the induced subgraph $〈S\cup T〉$ is connected. The set domination number of $G$ is the minimum cardinality of a set dominating set of $G$.

In [5], Sampathkumar and Pushpa Latha introduced the concept of point set domination which is a special case of set domination.

Definition 1.3

[5]

A set $D\subseteq V\left(G\right)$ is a point set dominating set (or in short, psd-set) of a graph $G$ if for every subset $S\subseteq V-D$ there exists a vertex $v\in D$ such that the induced subgraph $〈S\cup \left\{v\right\}〉$ is connected. The point set domination number of $G$ is the minimum cardinality of a point set dominating set of $G$.

Point-set domination has been studied further by Acharya and Gupta [6,7]. In this paper we consider another special case of Set-domination, namely, 2-point set domination which is defined as follows.

Definition 1.4

[8]

A set $D\subseteq V\left(G\right)$ is a 2-point set dominating set (or in short, 2-psd set) of a graph $G$ if for every subset $S\subseteq V-D$ there exists a non-empty set $T\subseteq D$ containing at most two vertices such that the induced subgraph $〈S\cup T〉$ is connected.

The set of all 2-psd sets of $G$ is denoted by ${\mathcal{D}}_{2ps}\left(G\right)$.

The following theorem is immediate from the definition of 2-point set dominating set and we will be using this result frequently throughout the paper.

Theorem 1.5

A subset $D\subseteq V\left(G\right)$ is a $2$-psd set of a graph $G$ if and only if for every independent set $S\subseteq V-D$ there exists a set $T\subseteq D$ such that $〈S\cup T〉$ is connected.

Proof

The condition is necessary by definition. Conversely, let $S$ be any subset of $V-D$ and let $S^{\prime }$ be a maximal independent subset of $S$. Then there exists a set $T\subseteq D$ such that $\left|T\right|\le 2$ and $〈S^{\prime }\cup T〉$ is connected, which in turn implies that $〈S\cup T〉$ is connected.  □

Clearly, every point set dominating set of $G$ is a 2-point set dominating set and every 2-point set dominating set is a dominating set of $G$. However, the converse of the above implications is not true.

We observe that point-set domination and 2-point set domination are superhereditary properties. Hence a 2-psd set (psd-set) $D$ is minimal if and only if $D-\left\{d\right\}$ is not a 2-psd set (psd-set) for all $d\in D$. The main focus of this paper is the characterization of minimal 2-psd sets.

2 Minimal 2-psd sets in a graph

We first give a characterization of minimal 2-psd sets of a general graph.

Theorem 2.1

A $2$-psd set $D$ of a graph $G$ is minimal if and only if for every $d\in D$ one of the following holds:

(a)	$N\left(d\right)\cap D=\varphi$.

(b)

There exists an independent subset $S\subseteq (V-D)\cup \left\{d\right\}$ such that $S⁄\subseteq N\left(u\right)$ for every $u\in D-\left\{d\right\}$and for any two distinct vertices $x,y\in D-\left\{d\right\}$with $N\left(x\right)\cup N\left(y\right)\supseteq S$, $x$ and $y$ are non-adjacent and $N\left(x\right)\cap N\left(y\right)\cap S=\varphi$.

Proof

Let $D$ be a minimal 2-psd set of $G$ and let $d\in D$. Then $D-\left\{d\right\}$ is not a 2-psd set of $G$. If $d$ is not dominated by $D-\left\{d\right\}$, then $N\left(d\right)\cap D=\varphi$. Now suppose $d$ is dominated by $D-\left\{d\right\}$. Since $D-\left\{d\right\}$ is not a 2-psd set of $G$, there exists an independent subset $S\subseteq (V-D)\cup \left\{d\right\}$ such that for all $T\subseteq D-\left\{d\right\}$ with $\left|T\right|\le 2$, the induced subgraph $〈S\cup T〉$ is not connected. Hence it follows that $S⁄\subseteq N\left(u\right)$ for all $u\in D-\left\{d\right\}$. Now, let $T=\{x,y\}\subseteq D-\left\{d\right\}$ and suppose $N\left(x\right)\cup N\left(y\right)\supseteq S$. Let $a,b\in S$. If both $a,b\in N\left(x\right)$ or both $a,b\in N\left(y\right)$, then $(a,x,b)$ or $(a,y,b)$ is an $a$-$b$ path in $〈S\cup T〉$. Suppose $a\in N\left(x\right)$ and $b\in N\left(y\right)$. If $xy\in E\left(G\right)$, then $(a,x,y,b)$ is an $a$-$b$ path in $〈S\cup T〉$. If $N\left(x\right)\cap N\left(y\right)\cap S\ne \varphi$, then $(a,x,c,y,b)$ where $c\in N\left(x\right)\cap N\left(y\right)\cap S$, is an $a$-$b$ path in $〈S\cup T〉$. Hence $〈S\cup T〉$ is connected which is a contradiction. Thus if $N\left(x\right)\cup N\left(y\right)\supseteq S$, then $xy⁄\in E\left(G\right)$ and $N\left(x\right)\cap N\left(y\right)\cap S=\varphi$.

Conversely, suppose that for every $d\in D$ either (i) or (ii) holds. If (i) holds, then $D-\left\{d\right\}$ is not a dominating set of $G$. If (ii) holds, then for the subset $S\subseteq (V-D)\cup \left\{d\right\}$, the induced subgraph $〈S\cup T〉$ is disconnected for all $T\subseteq D-\left\{d\right\}$ with $\left|T\right|=1$ or $\left|T\right|=2$. Hence, $D-\left\{d\right\}$ is not a 2-psd set of $G$, so that $D$ is a minimal 2-psd set.  □

We now proceed to consider the problem of characterizing minimal 2-psd sets in separable graphs. The structure of the graph leads to specific and explicit characterization of minimal 2-psd sets. We consider separately 2-psd sets $D$ for which $V-D$ is contained in a single block or contained in union of all blocks at a particular cut-vertex $w$ and the remaining cases and obtain necessary and sufficient conditions for minimality for each of the cases.

Theorem 2.2

Let $D$ be a $2$-psd set of a separable graph $G$ of order $n$ and let $\left|D\right|=n-1$. Then $D$ is a minimal $2$-psd set of $G$ if and only if $G\cong K_{1,n-1}$ and $D$ is the set of all pendant vertices of $G$.

Proof

Let $V-D=\left\{v\right\}$. Suppose $D$ is a minimal 2-psd set of $G$. If there exist two adjacent vertices $x,y\in D$, then either $D-\left\{x\right\}$ or $D-\left\{y\right\}$ is a 2-psd set of $G$ which is a contradiction. Hence $D$ is independent and $G\cong K_{1,n-1}$. The converse is obvious.  □

Theorem 2.3

Let $G$ be a separable graph and let $D$ be a $2$-psd set of $G$ such that $\left|D\right|\le n-2$ and $V-D⊊V\left(B\right)$ for some block $B$ of $G$. Then $D$ is a minimal $2$-psd set of $G$ if and only if for every $d\in D$ one of the following holds:

(i)	$d\in V\left(B_1\right)$ for some block $B_1\ne B$ and the cut-vertex $w\in V\left(B\right)\cap V\left(B_1\right)$ belongs to $V-D$.

(ii)	$d\in V\left(B\right)\cap D$ and $N\left(d\right)\cap D=\varphi$.

(iii)

There exists an independent set $S\subseteq (V-D)\cup \left\{d\right\}$such that $S⁄\subseteq N\left(x\right)$ for any $x\in D-\left\{d\right\}$ and if $S\subseteq N\left(x\right)\cup N\left(y\right)$ for some $x,y\in D-\left\{d\right\}$, then $xy⁄\in E\left(G\right)$ and $N\left(x\right)\cap N\left(y\right)\cap S=\varphi$.

Proof

Let $D$ be a minimal 2-psd set of $G$ and let $d\in D$. Let $d\in V\left(B_1\right)$ for some block $B_1\ne B$ and suppose $d$ does not satisfy condition (i). This implies $N\left(d\right)\cap D\ne \varphi$. Since $D-\left\{d\right\}$ is not a 2-psd set of $G$, there exists an independent set $S\subseteq (V-D)\cup \left\{d\right\}$ such that $S⁄\subseteq N\left(x\right)$ for any $x\in D-\left\{d\right\}$ and if $S\subseteq N\left(x\right)\cup N\left(y\right)$ for some $x,y\in D-\left\{d\right\}$, then $xy⁄\in E\left(G\right)$ and $N\left(x\right)\cap N\left(y\right)\cap S=\varphi$. Thus $d$ satisfies condition (iii). Similarly we can prove that, if $d\in V\left(B\right)\cap D$ and does not satisfy condition (ii), then $d$ satisfies condition (iii).

Conversely, let each $d\in D$ satisfy one of the conditions (i), (ii) and (iii). We shall show that $D$ is minimal. Let $d\in D$. If $d$ satisfies condition (i) then for any $x\in V-D$, $〈(D-\left\{d\right\})\cup \{d,x\}〉$ does not contain any $d$-$x$ path and therefore, $D-\left\{d\right\}$ is not a 2-psd set of $G$. If $d$ satisfies condition (ii), then $D-\left\{d\right\}$ is not a dominating set and hence is not a 2-psd set of $G$. If $d$ satisfies condition (iii), then for the independent set $S$, there does not exist any $W\subseteq D$ such that $\left|W\right|\le 2$ and $〈S\cup W〉$ is connected. Thus $D-\left\{d\right\}$ is not a 2-psd set of $G$. Hence $D$ is minimal.  □

Theorem 2.4

Let $G$ be a separable graph and let $D$ be a $2$-psd set of $G$ such that $V-D=V\left(B\right)$ for some block $B$ of $G$. Then $D$ is a minimal $2$-psd set of $G$.

Proof

Let $d\in D$. Since $V-D=V\left(B\right)$, $d\in V\left(B_1\right)$ for some block $B_1\ne B$. Choose a vertex $u\in V\left(B\right)$ such that $u⁄\in V\left(B\right)\cap V\left(B_1\right)$. Then for $S=\{d,u\}$ there does not exist any set $T\subseteq D-\left\{d\right\}$ such that $\left|T\right|\le 2$ and $〈S\cup T〉$ is connected. Thus $D-\left\{d\right\}$ is not a 2-psd set for any $d\in D$ and hence $D$ is minimal.  □

In Theorems 2.2, 2.3 and 2.4 we have obtained a characterization of minimal 2-psd sets $D$ of a separable graph for which $V-D$ is contained in a block of $G$. We now proceed to characterize minimal 2-psd sets for which $V-D$ contains vertices from more than one block. For any cut-vertex $w\in G$, let ${\mathcal{B}}_w\left(G\right)$ denote the set of all blocks of $G$ containing $w$. For the rest of the paper $D$ stands for a 2-psd set of a separable graph $G$ for which $V-D$ contains vertices from more than one block.

Proposition 2.5

Let $G$ be a separable graph and let $v$ be a cut vertex of $G$. Let $D$ be a $2$-psd set of $G$ such that $v⁄\in D$. Then all vertices of $V-D$ are contained in one component of $G-v$.

Proof

Suppose $V-D$ contains vertices of different components of $G-v$. Let $v_1$ and $v_2$ be two different vertices of $V-D$ lying in two different components of $G-v$ and let $S=\{v_1,v_2\}$. Since any $v_1$-$v_2$ path contains vertex $v$ and $v⁄\in D$, there does not exist a subset $T\subseteq D$ such that $\left|T\right|\le 2$ and $〈S\cup T〉$ is connected. Hence $D$ is not a 2-psd set of $G$, which is a contradiction.  □

Proposition 2.6

Let $D$ be a $2$-psd set of a separable graph $G$ such that $V-D⊊{\cup }_{B\in {\mathcal{B}}_w\left(G\right)}V\left(B\right)$ for some cut-vertex $w\in V\left(G\right)$. Then $(V-D)\cap V\left(B\right)⊊N\left(w\right)$ for all blocks $B\in {\mathcal{B}}_w\left(G\right)$ except possibly for one block.

Proof

Let $u\in (V-D)\cap V\left(B\right)$ for some block $B\in {\mathcal{B}}_w\left(G\right)$. Suppose $u⁄\in N\left(w\right)$. Let $v\in (V-D)\cap V\left(B_1\right)$, where $B_1\ne B$ and $B_1\in {\mathcal{B}}_w\left(G\right)$. If $v$ is not adjacent to $w$, then $d(u,v)\ge 4$ which is a contradiction. Thus, every vertex of $(V-D)\cap V\left(B_1\right)$ where $B_1\ne B$ and $B_1\in {\mathcal{B}}_w\left(G\right)$ is adjacent to $w$.  □

Theorem 2.7

Let $D$ be a $2$-psd set of a separable graph $G$ such that $V-D\subseteq N\left(w\right)$ for some cut-vertex $w\in D$. Then $D$ is a minimal $2$-psd set of $G$ if and only if $V-D=N\left(w\right)$.

Proof

Suppose $D$ is a minimal 2-psd set of $G$. If $V-D⊊N\left(w\right)$, then $D^{\prime }=V\left(G\right)-N\left(w\right)$ is a 2-psd set of $G$ which contradicts the minimality of $D$. Hence $V-D=N\left(w\right)$.

Conversely, Suppose $V-D=N\left(w\right)$. We shall show that $D$ is a minimal 2-psd set of $G$. If not, there exists $d\in D$ such that $D^{\prime }=D-\left\{d\right\}$ is a 2-psd set of $G$. Choose two vertices $x,y\in V-D$ belonging to two different blocks of ${\mathcal{B}}_w\left(G\right)$. We consider three cases:

Case I: $d$ is adjacent to both $x$ and $y$.

In this case $(x,d,y,w,x)$ is a cycle containing vertices of different blocks of $G$, which is a contradiction.

Case II: $d$ is adjacent to $x$ but not to $y$.

Now, for the set $\{d,y\}$ there exists $W_1\subseteq D^{\prime }$ such that $\left|W_1\right|\le 2$ and $〈W_1\cup \{d,y\}〉$ is connected. Since $N\left(w\right)=V-D$, it follows that $w⁄\in W_1$. Now, let $P_1$ be a $y$-$d$ path in $〈W_1\cup \{d,y\}〉$. Then $(x,w,y,P_1,d,x)$ is a cycle containing vertices of different blocks of $G$, which is a contradiction.

Case III: $d$ is adjacent to neither $x$ nor $y$.

For the subsets $\{d,x\}$ and $\{d,y\}$, there exist $W_2,W_3\subseteq D^{\prime }$ such that $\left|W_2\right|,\left|W_3\right|\le 2$ and $〈W_2\cup \{d,x\}〉$ and $〈W_2\cup \{d,y\}〉$ are connected. Now all $x$-$y$ paths pass through $w$ and hence $w\in W_2\cup W_3$. This implies that $N\left(w\right)\cap D\ne \varphi$, which contradicts our assumption that $N\left(w\right)=V-D$.

Thus there does not exist any $d\in D$ such that $D-\left\{d\right\}$ is a 2-psd set of $G$ and hence $D$ is a minimal 2-psd set.  □

Theorem 2.8

Let $D$ be a $2$-psd set of a separable graph $G$ such that $V-D⁄\subseteq N\left(w\right)$ for any cut-vertex $w$ of $G$. Let $w$ be a cut-vertex of $G$ such that $w\in D$, $V\left(B\right)\cap (V-D)⁄\subseteq N\left(w\right)$ and $(V-D)-V\left(B\right)⊊N\left(w\right)$ for some block $B\in {\mathcal{B}}_w\left(G\right)$. Then $V\left(B\right)$ can be partitioned into four subsets $S\left(B\right),R\left(B\right),V_3$ and $V_4$ where $S\left(B\right)=N\left(w\right)\cap V\left(B\right)\cap D$, $R\left(B\right)=\{V\left(B\right)\cap (V-D)\}-N\left(w\right),V_3=V\left(B\right)\cap (V-D)\cap N\left(w\right)$ and $V_4=\{V\left(B\right)\cap D\}-N\left(w\right)$. Further, $S\left(B\right)$ is a psd set of $〈S\left(B\right)\cup R\left(B\right)〉$.

Proof

Since $V\left(B\right)\cap (V-D)⁄\subseteq N\left(w\right)$, $R\left(B\right)$ is non-empty. We now prove that $S\left(B\right)$ is non-empty. Let $x\in R\left(B\right)$ and $y\in (V-D)-V\left(B\right)$. For the set $\{x,y\}\subseteq V-D$, there exists a set $W\subseteq D$ such that $\left|W\right|\le 2$ and $〈\{x,y\}\cup W〉$ is connected. Since $x,y$ belong to two different blocks of ${\mathcal{B}}_w\left(G\right)$, by Proposition 2.5, $w\in W$. Also there exists $w_1\in W$ such that $w_1\in N\left(w\right)\cap V\left(B\right)\cap D$ and $(x,w_1,w,y)$ is a path in $G$. This proves that $S\left(B\right)=N\left(w\right)\cap V\left(B\right)\cap D$ is non-empty.

We now claim that $S\left(B\right)$ is a psd-set of $S\left(B\right)\cup R\left(B\right)$. Let $T$ be an independent subset of $R\left(B\right)$ and $x\in (V-D)-V\left(B\right)$. Since $D$ is a 2-psd set of $G$, there exists a set $Z\subseteq D$, such that $\left|Z\right|\le 2$ and $〈T\cup \left\{x\right\}\cup Z〉$ is connected. Since the vertices of $T$ and $x$ belong to two different blocks of ${\mathcal{B}}_w\left(G\right)$, $w\in Z$. Also no vertex of $T$ is adjacent to $w$ and hence there exists $u\in N\left(w\right)\cap V\left(B\right)\cap D$ such that $Z=\{w,u\}$ and $〈T\cup \left\{u\right\}〉$ is connected. Hence $S\left(B\right)$ is a psd set of $〈S\left(B\right)\cup R\left(B\right)〉$. Now,

$\begin{array}{ccc}S\left(B\right)\cup V_4\hfill & \hfill =\hfill & [V\left(B\right)\cap D\cap N\left(w\right)]\cup [\{V\left(B\right)\cap D\}-N\left(w\right)]\hfill \\ \hfill & \hfill =\hfill & V\left(B\right)\cap D.\hfill \end{array}$

Also,

$\begin{array}{ccc}R\left(B\right)\cup V_3\hfill & \hfill =\hfill & [V\left(B\right)\cap (V-D)\cap N\left(w\right)]\cup [\{V\left(B\right)\cap (V-D)\}-N\left(w\right)]\hfill \\ \hfill & \hfill =\hfill & V\left(B\right)\cap (V-D).\hfill \end{array}$

Hence,

$S\left(B\right)\cup R\left(B\right)\cup V_3\cup V_4=[S\left(B\right)\cup V_4]\cup [V_3\cup R\left(B\right)]=[V\left(B\right)\cap D]\cup [V\left(B\right)\cap (V-D)]=V\left(B\right).\square$

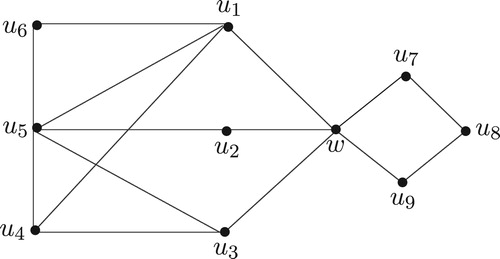
We illustrate the above theorem by a graph $G$ in Fig. 1. Consider the 2-psd sets $D_1=\{u_3,u_6,u_8,w\},D_2=\{u_1,u_2,u_8,w\}$ and $D_3=\{u_1,u_8,w\}$ of $G$. The corresponding pairs $(S_i\left(B\right),R_i\left(B\right))$ for $i=1,2,3$ of subsets of $V\left(B\right)$ such that $S_i\left(B\right)$ is a psd-set of $〈S_i\left(B\right)\cup R_i\left(B\right)〉$ are $S_1\left(B\right)=\left\{u_3\right\},R_1\left(B\right)=\{u_4,u_5\}$; $S_2\left(B\right)=\{u_1,u_2\},R_2\left(B\right)=\{u_4,u_5,u_6\}$ and $S_3\left(B\right)=\left\{u_1\right\},R_3\left(B\right)=\{u_4,u_5,u_6\}$ respectively.

Fig. 1 A graph to illustrate Theorem 2.8.

Theorem 2.9

Let $D$ be a $2$-psd set of a separable graph $G$ such that $V-D\subseteq {\bigcup }_{B\in {\mathcal{B}}_w\left(G\right)}V\left(B\right)$ for some cut-vertex $w\in D$. Let $B\in {\mathcal{B}}_w\left(G\right)$ be such that $(V-D)\cap V\left(B\right)⁄\subseteq N\left(w\right)$ and $(V-D)-V\left(B\right)⊊N\left(w\right)$. Then $D$ is a minimal 2-psd set of $G$ if and only if the following are true:

(a)	$(V-D)-V\left(B\right)=N\left(w\right)-V\left(B\right)$.

(b)	For every $d\in S\left(B\right)$, there exists an independent set $S\subseteq R\left(B\right)$ such that $S⁄\subseteq N\left(x\right)$ for any $x\in S\left(B\right)-\left\{d\right\}$.

(c)	For every $d\in V_4$ at least one of the following holds: (i) $N\left(d\right)\cap S\left(B\right)=\varphi$. (ii) There exists an independent set $S\subseteq R\left(B\right)\cup \left\{d\right\}$ such that $S⁄\subseteq N\left(x\right)$ for any $x\in S\left(B\right)$.

Proof

Suppose $D$ is a minimal 2-psd set of $G$. Since $(V-D)-V\left(B\right)⊊N\left(w\right)$, we have $(V-D)-V\left(B\right)\subseteq N\left(w\right)-V\left(B\right)$. Suppose $x\in \{N\left(w\right)-V\left(B\right)\}-\{(V-D)-V\left(B\right)\}$. Then $D-\left\{x\right\}$ is also a 2-psd set of $G$ which contradicts the minimality of 2-psd set $D$ of $G$. Thus, $(V-D)-V\left(B\right)=N\left(w\right)-V\left(B\right)$. This proves condition (a).

Now suppose (b) is not true. Therefore there exists a vertex $d\in S\left(B\right)$ such that every independent set $S\subseteq R\left(B\right)$ is contained in $N\left(x\right)$ for some $x\in S\left(B\right)-\left\{d\right\}$. Let $D^{\prime }=D-\left\{d\right\}$ and let $Z$ be any independent subset of $V-D^{\prime }$. Then $Z\cap N\left(w\right)\subseteq N\left(w\right)$ and $Z-N\left(w\right)\subseteq R\left(B\right)$. Since $S\left(B\right)$ is a psd-set of $〈S\left(B\right)\cup R\left(B\right)〉$, there exists a vertex $d^{\prime }\in S\left(B\right)$ such that $Z-N\left(w\right)\subseteq N\left(d^{\prime }\right)$. Also since condition (b) is not true for $d$, $d^{\prime }\ne d$. Thus, $〈Z\cup \{w,d^{\prime }\}〉$ is connected. Hence $D^{\prime }$ is a 2-psd set of $G$ which contradicts the minimality of $D$. This proves condition (b).

Now suppose condition (c) is not true for some $d\in V_4$. Then $d$ is adjacent to some vertex of $S\left(B\right)$ and for every independent set $S\subseteq R\left(B\right)\cup \left\{d\right\}$, there exists $x\in S\left(B\right)$ such that $S\subseteq N\left(x\right)$. Let $D^{\prime }=D-\left\{d\right\}$ and let $Z\subseteq V-D^{\prime }$ be an independent set. If $d⁄\in Z$, then since $S\left(B\right)$ is a psd-set of $〈S\left(B\right)\cup R\left(B\right)〉$, there exists $u\in S\left(B\right)$ such that $〈Z\cup \{u,w\}〉$ is connected. Now if $d\in Z$, then since condition (c)(ii) is not true, there exists a $v\in S\left(B\right)$ such that $〈Z\cup \{v,w\}〉$ is connected. Thus $D-\left\{d\right\}$ is a 2-psd set of $G$ which contradicts the minimality of $D$. This proves condition (c).

Conversely, suppose conditions (a),(b) and (c) are satisfied. Suppose there exists $d_0\in D$ such that $D-\left\{d_0\right\}$ is a 2-psd set of $G$. We consider two cases:

Case I: $d_0⁄\in V\left(B\right)$.

Let $x\in R\left(B\right)$. Since $d_0$ and $x$ belong to two different blocks of ${\mathcal{B}}_w\left(G\right)$, every $d_0$-$x$ path must pass through $w$. Since, $x\in R\left(B\right)$, $d(x,w)\ge 2$. Also, $d_0\in D$ and $N\left(w\right)-V\left(B\right)=(V-D)-V\left(B\right)$. Hence $d(d_0,w)\ge 2$ which in turn implies that $d(d_0,x)\ge 4$ which is a contradiction.

Case II: $d_0\in V\left(B\right)$.

Since $V\left(B\right)\cap D=S\left(B\right)\cup V_4$, $d_0\in S\left(B\right)$ or $d_0\in V_4$. Suppose $d_0\in S\left(B\right)$. Let $S$ be an independent subset of $R\left(B\right)$ and let $x\in (V-D)-V\left(B\right)$. Since $D^{\prime }$ is a 2-psd set of $G$, there exists $W_1\subseteq D^{\prime }$, such that $\left|W_1\right|\le 2$ and $〈W_1\cup \{S\cup \left\{x\right\}\}〉$ is connected. Since the vertices of $S$ and $x$ are from different blocks of ${\mathcal{B}}_w\left(G\right)$, $w\in W_1$. Since $S$ is an independent subset of $R\left(B\right)$ there exists a vertex $w_1\in S\left(B\right)-\left\{d_0\right\}$ such that $W_1=\{w,w_1\}$ and $S\subseteq N\left(w_1\right)$. It is true for every independent subset $S$ of $R\left(B\right)$ which contradicts condition (b).

Suppose $d_0\in V_4$. We claim that $N\left(d_0\right)\cap S\left(B\right)\ne \varphi$. Let $x\in (V-D)-V\left(B\right)$. Since $D^{\prime }$ is a 2-psd set of $G$, there exists a set $W_2\subseteq D^{\prime }$ such that $\left|W_2\right|\le 2$ and $〈\{d_0,x\}\cup W_2〉$ is connected. Since $d_0$ and $x$ belong to different blocks of ${\mathcal{B}}_w\left(G\right)$, $w\in W_2$ and again since $d_0$ is not adjacent to $w$, $W_2=\{w,w_2\}$ for some $w_2\in S\left(B\right)$. This shows that $d_0\in N\left(w_2\right)$. Hence $N\left(d_0\right)\cap S\left(B\right)\ne \varphi$. Thus condition (c)(i) does not hold.

Now let $S$ be an independent subset in $R\left(B\right)\cup \left\{d_0\right\}$ and let $x\in (V-D)-V\left(B\right)$. Since $D^{\prime }$ is a 2-psd set of $G$, there exists a set $W_3\subseteq D^{\prime }$ such that $\left|W_3\right|\le 2$ and $〈W_3\cup S\cup \left\{x\right\}〉$ is connected. Since $x⁄\in V\left(B\right)$, $w\in W_3$. Further, since $S\subseteq R\left(B\right)\cup \left\{d_0\right\}$, $W_3=\{w,w_3\}$ for some $w_3\in S\left(B\right)$ and $S\subseteq N\left(w_3\right)$. Hence condition (c)(ii) does not hold.

Thus in all cases we get a contradiction. Hence $D$ is a minimal 2-psd set.  □

Theorem 2.10

Let $D$ be a $2$-psd set of a separable graph $G$ such that $V-D⁄\subseteq {\bigcup }_{B\in {\mathcal{B}}_w\left(G\right)}V\left(B\right)$ for any cut-vertex $w\in V\left(G\right)$. Then there exists a pair of adjacent cut-vertices $w_1$ and $w_2$ of $G$ such that $V-D\subseteq N\left(w_1\right)\cup N\left(w_2\right)$.

Proof

Since $V-D⁄\subseteq {\bigcup }_{B\in {\mathcal{B}}_w\left(G\right)}V\left(B\right)$ for any cut-vertex $w\in V\left(G\right)$, there exist $u_1,u_2\in V-D$ such that $u_1\in V\left(B_1\right)$ and $u_2\in V\left(B_2\right)$ and the blocks $B_1$ and $B_2$ have no common cut-vertex.

Consider the set $\{u_1,u_2\}\subseteq V-D$. Since $D$ is a 2-psd set of $G$, there exists a set $W\subseteq D$ such that $\left|W\right|\le 2$ and $〈\{u_1,u_2\}\cup W〉$ is connected. Since blocks $B_1$ and $B_2$ have no common cut-vertex, $\left|W\right|\ne 1$. Let $W=\{w_1,w_2\}$. Then $(u_1,w_1,w_2,u_2)$ is a path in $G$. Since $u_1$ and $u_2$ belong to two different blocks with no common cut-vertex, $w_1$ and $w_2$ are cut vertices and are adjacent.

We claim that $V-D\subseteq N\left(w_1\right)\cup N\left(w_2\right)$. Let $u_3\in V-D$ be such that $u_3⁄\in N\left(w_1\right)\cup N\left(w_2\right)$. Since $D$ is a 2-psd set of $G$, for the set $\{u_1,u_2,u_3\}$, there exists a subset $W_1\subseteq D$ such that $\left|W_1\right|\le 2$ and $〈W_1\cup \{u_1,u_2,u_3\}〉$ is connected. Since every $u_1$-$u_2$ path passes through $w_1$ and $w_2$, $W_1=\{w_1,w_2\}$. Since $u_3⁄\in N\left(w_1\right)\cup N\left(w_2\right)$ and $〈W\cup \{u_1,u_2,u_3\}〉$ is connected, $u_3$ is adjacent to either $u_1$ or $u_2$. Without loss of generality we may assume that $u_3\in N\left(u_1\right)$. Now for the set $\{u_3,u_2\}$, there exists a set $W_2\subseteq D$ such that $\left|W_2\right|\le 2$ and $〈W_2\cup \{u_3,u_2\}〉$ is connected. Since $u_3⁄\in N\left(w_1\right)\cup N\left(w_2\right)$, $W_2\ne W$. Therefore, there exists a $u_1$-$u_2$ path not containing $w_1$ which is a contradiction. Thus $u_3\in N\left(w_1\right)\cup N\left(w_2\right)$.

Hence $V-D\subseteq N\left(w_1\right)\cup N\left(w_2\right)$.  □

Theorem 2.11

Let $D$ be a $2$-psd set of a separable graph $G$ such that $V-D⁄\subseteq {\bigcup }_{B\in {\mathcal{B}}_w\left(G\right)}V\left(B\right)$ for any cut-vertex $w\in V\left(G\right)$. Then $D$ is minimal if and only if $V-D=\{N\left(w_1\right)\cup N\left(w_2\right)\}-\{w_1,w_2\}$for a pair of adjacent cut-vertices $w_1$ and $w_2$ in $D$.

Proof

Suppose $D$ is a minimal 2-psd set of $G$. By Theorem 2.10, $V-D\subseteq N\{w_1,w_2\}-\{w_1,w_2\}$ for a pair of adjacent cut-vertices $w_1$ and $w_2$ in $D$. If $V-D\ne \{N\left(w_1\right)\cup N\left(w_2\right)\}-\{w_1,w_2\}$ then $D^{\prime }=V\left(G\right)-[\{N\left(w_1\right)\cup N\left(w_2\right)\}-\{w_1,w_2\}]$ is a 2-psd set of $G$ which contradicts the minimality of $D$. Hence $V-D=\{N\left(w_1\right)\cup N\left(w_2\right)\}-\{w_1,w_2\}$.

Conversely, Suppose $D$ is a 2-psd set of $G$ such that $V-D=\{N\left(w_1\right)\cup N\left(w_2\right)\}-\{w_1,w_2\}$ for a pair of adjacent cut vertices $w_1,w_2\in D$. Suppose there exists $d\in D$ such that $D-\left\{d\right\}$ is a 2-psd set of $G$. Let $D^{\prime }=D-\left\{d\right\}$. Choose vertices $x\in N\left(w_1\right)-N\left(w_2\right)$ and $y\in N\left(w_2\right)-N\left(w_1\right)$. Since $V-D⊊V-D^{\prime }$, $x,y\in V-D^{\prime }$. Since $x$ and $y$ are non-adjacent vertices in $G$, there exists a set $W\in D^{\prime }$ such that $\left|W\right|\le 2$ and $〈W\cup \{x,y\}〉$ is connected. Let $P$ be the $x$-$y$ path in $〈W\cup \{x,y\}〉$. Since every $x$-$y$ path passes through $w_1$ and $w_2$, $W=\{w_1,w_2\}$. Thus, $d\ne w_1$ and $d\ne w_2$.

Now, three cases arise:

Case I: $d$ is adjacent to both $x$ and $y$.

In this case $(x,d,y,w_2,w_1,x)$ is a cycle containing vertices of different blocks of $G$ which is a contradiction.

Case II: $d$ is adjacent to $x$ and not to $y$.

For the set $\{d,y\}$ there exists $W_1\subseteq D^{\prime }$ such that $\left|W_1\right|\le 2$ and $〈W_1\cup \{d,y\}〉$ is connected. Since $\{N\left(w_1\right)\cup N\left(w_2\right)\}-\{w_1,w_2\}=V-D$, $w_1,w_2⁄\in W_1$. Now, let $P_1$ be a $y$-$d$ path in $〈W_1\cup \{d,y\}〉$. Then $(x,w_1,w_2,y,P_1,d,x)$ is a cycle containing vertices of different blocks of $G$ which is a contradiction.

Case III: $d$ is adjacent to neither $x$ nor $y$.

Then $\{d,x,y\}$ is an independent set in $V-D^{\prime }$. Therefore there exists $W_2\subseteq D^{\prime }$ such that $\left|W_2\right|\le 2$ and $〈W_2\cup \{d,x,y\}〉$ is connected. Since $\{N\left(w_1\right)\cup N\left(w_2\right)\}-\{w_1,w_2\}=V-D$, $w_1,w_2⁄\in W_2$. Let $P_2$ be a $x$-$y$ path in $〈W_2\cup \{d,x,y\}〉$. Then $(x,P_2,y,w_2,w_1,x)$ is a cycle in $G$ which is a contradiction to the fact that $x$ and $y$ are in different blocks of $G$.

Thus in all cases $D-\left\{d\right\}$ is not a 2-psd set of $G$ and hence $D$ is a minimal 2-psd set.  □

Notes

Peer review under responsibility of Kalasalingam University.