On cyclic orthogonal double covers of circulant graphs by special infinite graphs

Peer review under responsibility of Kalasalingam University.

Abstract

In this article, a technique to construct cyclic orthogonal double covers (CODCs) of regular circulant graphs by certain infinite graph classes such as complete bipartite and tripartite graphs and disjoint union of butterfly and $K_{1,2n-10}$ is introduced.

Keywords:

• Orthogonal double covers
• Orthogonal labelling
• Circulant graphs

1 Introduction

Let $H$ be a graph with vertex set $V$. A collection $\mathcal{G}={\left(G_v\right)}_{v\in V}$ of isomorphic spanning subgraphs (called pages) of $H$ is an orthogonal double cover (ODC) of $H$ by $G$ if the following two conditions hold

(1) Every edge in $H$ belongs to exactly two of the pages (double cover property) and

(2) $G_x$ and $G_y$ share an edge if and only if $x$ and $y$ are adjacent in $H$ (orthogonality).

This concept is a natural generalization of earlier definitions of an ODC for complete and complete bipartite graphs, that have been studied extensively (see the survey [1]). The necessary condition for an ODC of $H$ by $G$ is that $H$ is regular.

An effective technique to construct ODCs in the above cases was based on the idea of translating a given subgraph of $G$ by a group acting on $V\left(H\right)$.

The purpose of this article is to investigate the existence of cyclic orthogonal double covers of circulant graphs. The existence problem of ODCs by given graphs has attracted much attention during the last 10 years. The problem is known to be hard in general as it includes some long-standing open problems like the existence problems of biplanes as special cases. Also, the ODC problem originally stems from problems in database optimization and statistical design, and design theory. In [2,3], Demetrovics et al. investigated Armstrong database of minimum size for key and functional dependence. Armstrong database of size $n$ is equivalent to ODCs of $K_n$ whose pages consist of distinct cliques. The problem, however, subsequently earned a life of its own, resulting in a relatively rich literature, generalizing the problem to an expanding class of graphs, whereas the initial interest was connected to complete graphs. Research on ODCs has motivated the development of various direct and recursive methods for constructing ODCs. This article contains seven technical results (four theorems and three corollaries), regarding the existence of cyclic ODCs for certain classes of regular circulant graphs (of which complete graphs are a special case).

An automorphism of an ODC $\mathcal{G}={\left(G_v\right)}_{v\in V}$ of $H$ is a permutation $\sigma :V\left(H\right)⟶V\left(H\right)$ such that $\left\{\sigma {\left(G_v\right)}_{v\in V}\right\}=\mathcal{G}$ where $\sigma \left(G_v\right)$ is a subgraph of $H$ with $V\left(\sigma \left(G_v\right)\right)=\{\sigma \left(v\right):v\in V\left(G_v\right)\}$ and $E\left(\sigma \left(G_v\right)\right)=\{(\sigma \left(u\right),\sigma \left(v\right)):(u,v)\in E\left(G_v\right)\}.$ An ODC $\mathcal{G}$ of $H$ is cyclic (CODC) if the cyclic group of order $\left|V\left(H\right)\right|$ is a subgroup of the automorphism group of $\mathcal{G}$.

Let $\mathcal{B}$ be an Abelian group with identity $0\mathrm{.}$ $\mathrm{Let}$ $S$ be a subset of $\mathcal{B}$ satisfying $0⁄\in S$ and $S=-S$ -that is, $s\in S$ if and only if $-s\in S$. The Cayley graph Cay($\mathcal{B;}S$) on $\mathcal{B}$ with connection set $S$ is defined as follows (i) the vertices are the elements of $\mathcal{B}$ and (ii) there is an edge joining $u$ and $v$ if and only if $u=s+v$ for some $s\in S$. The Cayley graphs on cyclic groups have played a special role in the study of Cayley graphs. They are widely known as circulant graphs, because their adjacency matrices are circulant matrices. 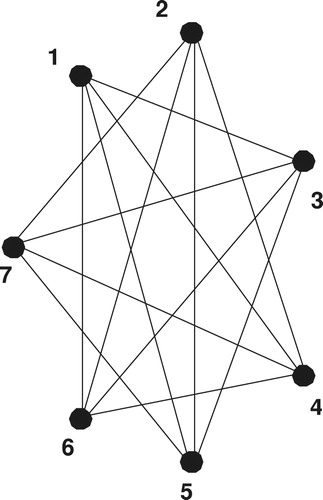We use the notation Circ($n\mathcal{;}S$) to denote the circulant graph of order $n$ with connection set $S.$ The length of an edge $(u,v)$ in Circ$(n;S),$ is defined by $d(u,v)=min\{\left|u-v\right|,n-\left|u-v\right|\}.$ An example, the circulant graph Circ($7\mathcal{;}\{2,3,4,5\}$) is given in Fig. 1.

Fig. 1 The circulant graph Circ($7;\{2,3,4,5\}$).

In this article we make use of the usual notation: $K_{m,n}$ for the complete bipartite graph with partition sets of sizes $m$ and $n$, $K_n$ for the complete graph on $n$ vertices, $G\cup F$ for the disjoint union of $G$ and $F$, $K_{m,n,k}$ for the complete tripartite graph with partition sets of sizes $m,n$ and $k$, $P_n$ for the path on $n$ vertices$,$ and $G\setminus F$ represents the graph obtained by removing the edges of a subgraph $F$ from the graph $G$, where the graphs $G$ and $F$ are spanning subgraphs of $H$. Let $k\ge 1,n_1,n_2,\dots ,n_k$ be positive integers, $n_1,n_k\ge 1$ and $n_i\ge 0$ for $i\in \{2,3,\dots ,k-1\},$ the caterpillar $C_k(n_1,n_2,\dots ,n_k)$ is the tree obtained from the path $P_k:=x_1{x}_2\dots x_k$ by joining vertex $x_i$ to $n_i$ new vertices, $i\in \{1,2,3,\dots ,k\}.$

Orthogonal labelling notion is introduced by the authors of [1]. Given a graph $G=(V,E)$ with $m-1$ edges, a $1-1$ mapping $\Psi :V\left(G\right)⟶{\mathbb{Z}}_m$ is an orthogonal labelling of $G$ if $\left(1\right)G$ contains exactly two edges of length $d\in \{1,2,\dots ,\lfloor \frac{(m-1)}{2}\rfloor \},$ and exactly one edge of length $m∕2$ if $m$ is even, and $\left(2\right)\{r\left(d\right):d\in \{1,2,\dots ,\lfloor \frac{(m-1)}{2}\rfloor \}\}=\{1,2,\dots ,\lfloor \frac{(m-1)}{2}\rfloor \}\mathrm{,}$ $\mathrm{where}$ $r\left(d\right)$ is the rotation-distance between two edges, see [1].

Gronau et al. [1] relates CODCs of $K_m$ and the orthogonal labelling by the following theorem.

Theorem 1

[1]

A CODC of $K_m$ by a graph $G$ exists if and only if there exists an orthogonal labelling of $G$.

The following theorem of Sampathkumar and Srinivasan is a generalization of Theorem 1.

Theorem 2

[4]

A CODC of $Circ(m;\left\{d_1,d_2,\dots ,d_k\right\})$ by a graph $G$ exists if and only if there exists an orthogonal $\left\{d_1,d_2,\dots ,d_k\right\}$-labelling of $G$.

For results on orthogonal double cover of circulant graphs, see [45–7]. In [18–10], other results of ODCs by different graph classes can be found. In [11], the other terminology not defined here can be found. We use Theorem 2 to prove the existence of CODC of circulant graphs by a graph $G$.

2 CODCs of circulant graphs by complete bipartite and tripartite graphs

Theorem 3

For all positive integers $n>1$, there exists a CODC of $4n-$regular Circ $(4n+2;\{1,2,\dots ,2n\})$ by $K_{2,2n}.$

Proof

Let us define $\Psi :V\left(K_{2,2n}\right)⟶{\mathbb{Z}}_{4n+2}$ by$\Psi \left(v_0\right)=0,\Psi \left(v_1\right)=2n+1,\Psi \left(v_j\right)=2n+j,$ where $2\le j\le n+1$, and $\Psi \left(v_j\right)=4n+1+j,$ where $n+2\le j\le 2n+1$. Then the edges of lengths $l$, where $1\le l\le n$, are $(\Psi \left(v_1\right),\Psi \left(v_{l+1}\right))$, and $(\Psi \left(v_1\right),\Psi \left(v_{n+l+1}\right)),$ and the edges of lengths $l$, where $n+1\le l\le 2n$ are $(\Psi \left(v_0\right),\Psi \left(v_{l-n+1}\right))$, and $(\Psi \left(v_0\right),\Psi \left(v_{l+1}\right)).$ Hence for $l\in \{1,2,\dots ,2n\},K_{2,2n}$ contains exactly two edges of length $l$, and since every two edges of the same length are adjacent $\{r\left(l\right):l\in \{1,2,\dots ,2n\}\}=\{1,2,\dots ,2n\}.$ Hence $K_{2,2n}$ has an orthogonal labelling.   $\square$

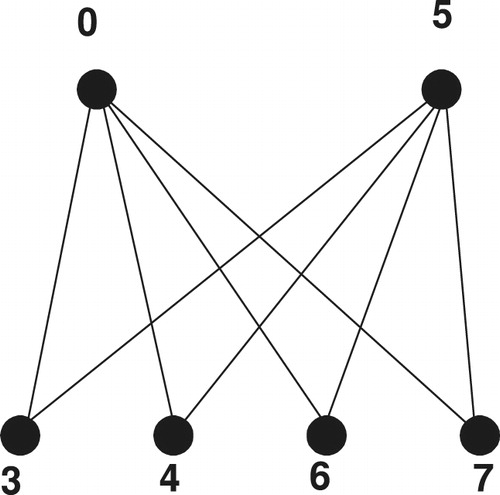
A CODC generating graph of $8-$regular Circ $(10;\{1,2,3,4\})$ by $K_{2,4},$ is shown in Fig. 2.

Fig. 2 CODC generating graph of $8-$regular Circ $(10;\{1,2,3,4\})$ by $K_{2,4}.$

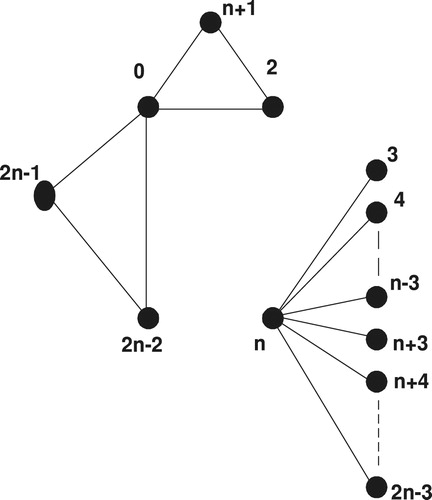
Theorem 4

For any positive integer $n\ge 5$, there exists a CODC of $(3n-1)-$regular Circ $(3n;\{1,2,\dots ,⌊\frac{3n}{2}⌋\})$ by $K_{1,2,n-1}.$

Proof

Let us define $\Psi :V\left(K_{1,2,n-1}\right)⟶{\mathbb{Z}}_{3n}$ by$\Psi \left(v_0\right)=0,\Psi \left(v_1\right)=2,\Psi \left(v_2\right)=4$, and $\Psi \left(v_j\right)=3j-6$, where $3\le j\le n+1$. $E\left(K_{1,2,n-1}\right)=\{\left\{(\Psi \left(v_0\right),\Psi \left(v_1\right))\right\}\cup \left\{(\Psi \left(v_0\right),\Psi \left(v_2\right))\right\}\cup \{(\Psi \left(v_0\right),\Psi \left(v_j\right)):3\le j\le n+1\}\cup \{(\Psi \left(v_1\right),\Psi \left(v_j\right)):3\le j\le n+1\}\cup \{(\Psi \left(v_2\right),\Psi \left(v_j\right)):3\le j\le n+1\}\}$.

Case 1. $n=2m+1;$ $m\ge 2$.

The edges of length $1$ are $(\Psi \left(v_1\right),\Psi \left(v_3\right))$ and $(\Psi \left(v_2\right),\Psi \left(v_3\right));$ the edges of length $2$ are $(\Psi \left(v_0\right),\Psi \left(v_1\right))$ and $(\Psi \left(v_2\right),\Psi \left(v_4\right));$ the edges of length $4$ are $(\Psi \left(v_0\right),\Psi \left(v_2\right))$ and $(\Psi \left(v_1\right),\Psi \left(v_4\right));$ the edges of length $3i$ where $1\le i\le m$ are $(\Psi \left(v_0\right),\Psi \left(v_{i+2}\right))$ and $(\Psi \left(v_0\right),\Psi \left(v_{2m+3-i}\right));$ the edges of length $3i+2$ where $1\le i\le m-1$ are $(\Psi \left(v_2\right),\Psi \left(v_{i+4}\right))$ and $(\Psi \left(v_1\right),\Psi \left(v_{2m+3-i}\right));$ the edges of length $3i+4$ where $1\le i\le m-1$ are $(\Psi \left(v_1\right),\Psi \left(v_{i+4}\right))$ and $(\Psi \left(v_2\right),\Psi \left(v_{2m+3-i}\right)).$ Hence for $l\in \{1,2,\dots ,⌊\frac{3n}{2}⌋\}$, $K_{1,2,n-1}$ contains exactly two edges of length $\{1,2,\dots ,⌊\frac{3n}{2}⌋\}$, and $\{r\left(l\right):\{1,2,\dots ,⌊\frac{3n}{2}⌋\}\}=\{1,2,\dots ,⌊\frac{3n}{2}⌋\}.$ Hence $K_{1,2,n-1}$ has an orthogonal labelling.

Case 2. $n=2m;$ $m\ge 3$.

The edge of length $3m$ is $(\Psi \left(v_0\right),\Psi \left(v_{m+2}\right));$ the edges of length $1$ are $(\Psi \left(v_1\right),\Psi \left(v_3\right))$ and $(\Psi \left(v_2\right),\Psi \left(v_3\right));$ the edges of length $2$ are $(\Psi \left(v_0\right),\Psi \left(v_1\right))$ and $(\Psi \left(v_2\right),\Psi \left(v_4\right));$ the edges of length $4$ are $(\Psi \left(v_0\right),\Psi \left(v_2\right))$ and $(\Psi \left(v_1\right),\Psi \left(v_4\right));$ the edges of length $3i$ where $1\le i\le m-1$ are $(\Psi \left(v_0\right),\Psi \left(v_{i+2}\right))$ and $(\Psi \left(v_0\right),\Psi \left(v_{2m+2-i}\right));$ the edges of length $3i+2$ where $1\le i\le m-1$ are $(\Psi \left(v_2\right),\Psi \left(v_{i+4}\right))$ and $(\Psi \left(v_1\right),\Psi \left(v_{2m+2-i}\right));$ the edges of length $3i+4$ where $1\le i\le m-2$ are $(\Psi \left(v_1\right),\Psi \left(v_{i+4}\right))$ and $(\Psi \left(v_2\right),\Psi \left(v_{2m+2-i}\right)).$ Hence for $l\in \{1,2,\dots ,\frac{3n}{2}-1\}$, $K_{1,2,n-1}$ contains exactly two edges of length $\{1,2,\dots ,\frac{3n}{2}-1\}$, and $\{r\left(l\right):\{1,2,\dots ,\frac{3n}{2}-1\}\}=\{1,2,\dots ,\frac{3n}{2}-1\}.$ Hence $K_{1,2,n-1}$ has an orthogonal labelling.   $\square$

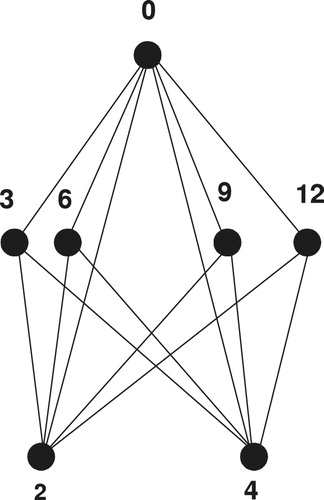
A CODC generating graph of $14-$regular Circ $(15;\{1,2,3,4,5,6,7\})$ by $K_{1,2,4}$, is shown in Fig. 3.

Fig. 3 CODC generating graph of $14-$regular Circ $(15;\{1,2,3,4,5,6,7\})$ by $K_{1,2,4}.$

3 CODCs of regular circulant graphs by certain graph $H^n$

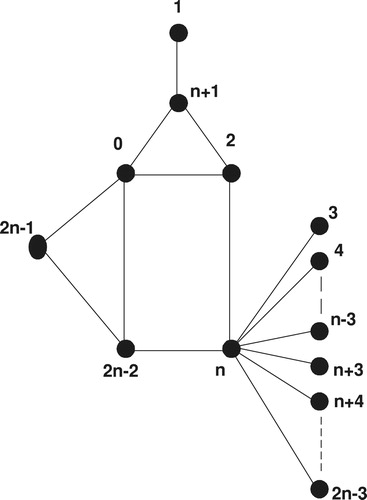
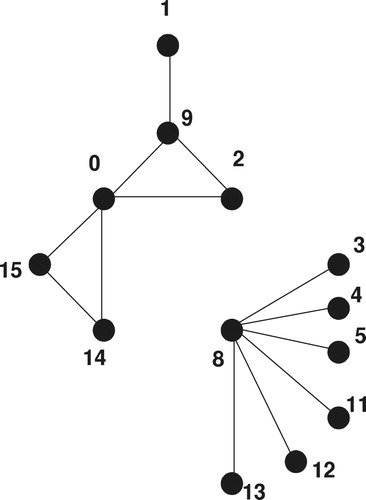
Let $H^n$ (as shown in Fig. 4) be a graph with the edge set:

Fig. 4 CODC generating graph of $(2n-1)-$regular Circ $(2n;\{1,2,\dots ,n\})$ by $H^n.$

$E\left(H^n\right)=\{(\Psi \left(v_1\right),\Psi \left(v_3\right)),(\Psi \left(v_0\right),\Psi \left(v_2\right)),(\Psi \left(v_3\right),\Psi \left(v_0\right)),(\Psi \left(v_3\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_4\right)),(\Psi \left(v_5\right),\Psi \left(v_4\right)),(\Psi \left(v_0\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right))\}\cup \{(\Psi \left(v_6\right),\Psi \left(v_{\alpha +4}\right)):3\le \alpha \le n-3\}\cup \{(\Psi \left(v_6\right),\Psi \left(v_{\beta -1}\right))\mathrm{:}n+3\le \beta \le 2n-3\}$, where $\Psi :V\left(H^n\right)⟶{\mathbb{Z}}_{2n}$ is defined by $\Psi \left(v_0\right)=0,\Psi \left(v_1\right)=1,\Psi \left(v_2\right)=2,\Psi \left(v_3\right)=n+1,\Psi \left(v_4\right)=2n-1,\Psi \left(v_5\right)=2n-2,\Psi \left(v_6\right)=n,\Psi \left(v_{\alpha +4}\right)=\alpha$, where $3\le \alpha$ $\le n-3,\Psi \left(v_{\beta -1}\right)=\beta$, where $n+3\le \beta \le 2n-3$. We denote by $V\left(H^n\right)$ the vertex set of the graph $H^n.$

Theorem 5

For all positive integers $n\ge 6$, there exists a CODC of $(2n-1)-$regular Circ $(2n;\{1,2,\dots ,n\})$ by $H^n.$

Proof

The edge of length $n$ is $(\Psi \left(v_1\right),\Psi \left(v_3\right)),$ the edges of length $1$ are $(\Psi \left(v_0\right),\Psi \left(v_4\right))$ and $(\Psi \left(v_5\right),\Psi \left(v_4\right));$ the edges of length $2$ are $(\Psi \left(v_0\right),\Psi \left(v_2\right))$ and $(\Psi \left(v_0\right),\Psi \left(v_5\right));$ the edges of length $l$ where $3\le l$ $\le n-3$ are $(\Psi \left(v_6\right),\Psi \left(v_{n-l+4}\right))$ and $(\Psi \left(v_6\right),\Psi \left(v_{l+n-1}\right));$ the edges of length $n-2$ are $(\Psi \left(v_6\right),\Psi \left(v_5\right))$ and $(\Psi \left(v_6\right),\Psi \left(v_2\right));$ the edges of length $n-1$ are $(\Psi \left(v_3\right),\Psi \left(v_0\right))$ and$(\Psi \left(v_3\right),\Psi \left(v_2\right))$. Hence for every $l\in \{1,2,\dots ,n\}$, $H^n$ contains exactly two edges of length $\{1,2,\dots ,n-1\},$ and exactly one edge of length $n$, and $\{r\left(l_1\right):l_1\in \{1,\dots ,n-1\}\}=\{1,\dots ,n-1\}$. Hence $H^n$ has an orthogonal labelling.   $\square$

A CODC generating graph of $15-$regular Circ $(16;\{1,2,3,4,5,6,7,8\})$ by $H^8$, is shown in Fig. 5.

Fig. 5 CODC generating graph of $15-$ regular Circ$(16;\{1,2,3,4,5,6,7,8\})$ by $H^8.$

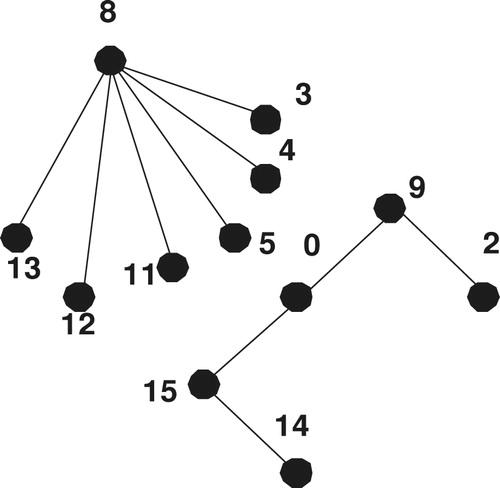
For the following Corollary, $E(H^n\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right))\})=\{(\Psi \left(v_1\right),\Psi \left(v_3\right)),(\Psi \left(v_0\right),\Psi \left(v_2\right)),(\Psi \left(v_3\right),\Psi \left(v_0\right)),(\Psi \left(v_3\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_4\right)),(\Psi \left(v_5\right),\Psi \left(v_4\right)),(\Psi \left(v_0\right),\Psi \left(v_5\right))\}\cup \{(\Psi \left(v_6\right),\Psi \left(v_{\alpha +4}\right)):3\le \alpha \le n-3\}\cup \{(\Psi \left(v_6\right),\Psi \left(v_{\beta -1}\right))\mathrm{:}n+3\le \beta \le 2n-3\},\text{where}\Psi :V(H^n\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right))\})⟶{\mathbb{Z}}_{2n}\text{is defined by}\Psi \left(v_0\right)=0,\Psi \left(v_1\right)=1,\Psi \left(v_3\right)=n+1,\Psi \left(v_4\right)=2n-1,\Psi \left(v_{\alpha +4}\right)=\alpha ,\text{where}3\le \alpha \le n-3,\Psi \left(v_{\beta -1}\right)=\beta ,\text{where}n+3\le \beta \le 2n-3.$

Corollary 6

For all positive integers $n\ge 6$, there exists a CODC of $(2n-3)-$regular Circ $(2n;\{\{1,2,\dots ,n\}\setminus \{n-2\}\})$ by $H^n\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right))\}.$

Proof

The edge of length $n$ is $(\Psi \left(v_1\right),\Psi \left(v_3\right)),$ the edges of length $1$ are $(\Psi \left(v_0\right),\Psi \left(v_4\right))$ and $(\Psi \left(v_5\right),\Psi \left(v_4\right));$ the edges of length $2$ are $(\Psi \left(v_0\right),\Psi \left(v_2\right))$ and $(\Psi \left(v_0\right),\Psi \left(v_5\right));$ the edges of length $l$ where $3\le l$ $\le n-3$ are $(\Psi \left(v_6\right),\Psi \left(v_{n-l+4}\right))$ and $(\Psi \left(v_6\right),\Psi \left(v_{l+n-1}\right));$ the edges of length $n-1$ are $(\Psi \left(v_3\right),\Psi \left(v_0\right))$ and$(\Psi \left(v_3\right),\Psi \left(v_2\right))$. Hence for every $l\in \{1,2,\dots ,n\}\setminus \{n-2\}$, $H^n\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right))\}$ contains exactly two edges of length $\{1,2,\dots ,n-1\}\setminus \{n-2\}$, and exactly one edge of length $n$, and $\{r\left(l_1\right):l_1\in \{1,\dots ,n-1\}\setminus \{n-2\}\}=\{1,\dots ,n-1\}\setminus \{n-2\}$. Hence $H^n\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right))\}$ has an orthogonal labelling.   $\square$

A CODC generating graph of $13-$regular Circ $(16;\{1,2,3,4,5,7,8\})$ by $H^8\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right))\}$, is shown in Fig. 6.

Fig. 6 CODC generating graph of $13-$regular Circ $(16;\{1,2,3,4,5,7,8\})$ by $H^8\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right))\}.$

For the following Corollary, $E(H^n\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_5\right))\})=\{(\Psi \left(v_1\right),\Psi \left(v_3\right)),(\Psi \left(v_3\right),\Psi \left(v_0\right)),(\Psi \left(v_3\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_4\right)),(\Psi \left(v_5\right),\Psi \left(v_4\right))\}\cup \{(\Psi \left(v_6\right),\Psi \left(v_{\alpha +4}\right)):3\le \alpha \le n-3\}$ $\cup \{(\Psi \left(v_6\right),\Psi \left(v_{\beta -1}\right))\mathrm{:}n+3\le \beta \le 2n-3\},\text{where}\Psi :V(H^n\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_5\right))\})⟶{\mathbb{Z}}_{2n}\text{is defined by}\Psi \left(v_1\right)=1,\Psi \left(v_3\right)=n+1,\Psi \left(v_4\right)=2n-1,\Psi \left(v_{\alpha +4}\right)=\alpha ,\text{where}3\le \alpha \le n-3,\Psi \left(v_{\beta -1}\right)=\beta ,\text{where}n+3\le \beta \le 2n-3.$

Also, we denote by $C_3(1,0,2)$ the caterpillar $C_k(n_1,n_2,\dots ,n_k)$ with $k=3,n_1=1,n_2=0,$ and $n_3=2.$

Corollary 7

For all positive integers $n\ge 6$, there exists a CODC of $(2n-5)-$regular Circ $(2n;\{\{1,2,4,\dots ,n\}\setminus \{2,n-2\}\})$ by $C_3(1,0,2)\cup K_{1,2n-10}\cong H^n\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_5\right))\}.$

Proof

The edge of length $n$ is $(\Psi \left(v_1\right),\Psi \left(v_3\right)),$ the edges of length $1$ are $(\Psi \left(v_0\right),\Psi \left(v_4\right))$ and $(\Psi \left(v_5\right),\Psi \left(v_4\right));$ the edges of length $l$ where $3\le l$ $\le n-3$ are $(\Psi \left(v_6\right),\Psi \left(v_{n-l+4}\right))$ and $(\Psi \left(v_6\right),\Psi \left(v_{l+n-1}\right));$ the edges of length $n-1$ are $(\Psi \left(v_3\right),\Psi \left(v_0\right))$ and$(\Psi \left(v_3\right),\Psi \left(v_2\right))$. Hence for every $l\in \{1,2,\dots ,n\}\setminus \{2,n-2\}$, $H^n\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_5\right))\}$ contains exactly two edges of length $\{1,2,\dots ,n-1\}\setminus \{2,n-2\}$, and exactly one edge of length $n$, and $\{r\left(l_1\right):l_1\in \{1,\dots ,n-1\}\setminus \{2,n-2\}\}=\{1,\dots ,n-1\}\setminus \{2,n-2\}$. Hence $H^n\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_5\right))\}$ has an orthogonal labelling.   $\square$

A CODC generating graph of $11-$regular Circ $(16;\{1,3,4,5,7,8\})$ by $H^8\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_5\right))\}\cong C_3(1,0,2)\cup K_{1,6}$, is shown in Fig. 7.

Fig. 7 CODC generating graph of $11-$regular Circ $(16;\{1,3,4,5,7,8\})$ by $H^8\setminus \{(\Psi \left(v_6\right),\Psi \left(v_5\right)),(\Psi \left(v_6\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_2\right)),(\Psi \left(v_0\right),\Psi \left(v_5\right))\}\cong C_3(1,0,2)\cup K_{1,6}.$

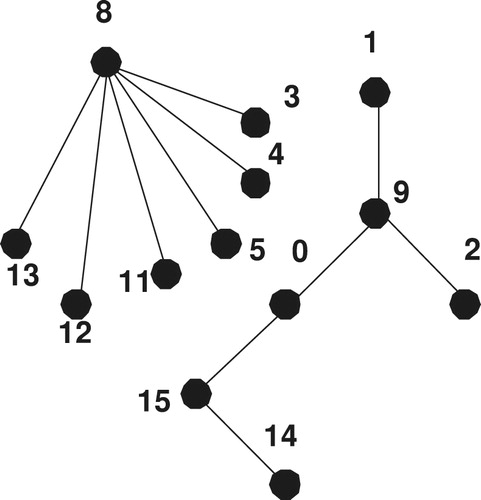
4 CODCs of regular circulant graphs by disjoint union of butterfly and $K_{1,2n-10}$

Let $G^n$(as shown in Fig. 8) be a graph with the edge set: $E\left(G^n\right)=E(\text{Butterfly}\cup K_{1,2n-10})=\{(\Psi \left(v_2\right),\Psi \left(v_0\right)),(\Psi \left(v_2\right),\Psi \left(v_1\right)),(\Psi \left(v_0\right),\Psi \left(v_4\right)),(\Psi \left(v_0\right),\Psi \left(v_1\right)),(\Psi \left(v_0\right),\Psi \left(v_3\right)),(\Psi \left(v_4\right),\Psi \left(v_3\right))\}$ $\cup \{(\Psi \left(v_5\right),\Psi \left(v_{\alpha +3}\right)):3\le \alpha \le n-3\}\cup \{(\Psi \left(v_5\right),\Psi \left(v_{\beta -2}\right)):n+3\le \beta \le 2n-3\},$ where $\Psi :V\left(G^n\right)⟶{\mathbb{Z}}_{2n}$ is defined by $\Psi \left(v_0\right)=0,\Psi \left(v_1\right)=2,\Psi \left(v_2\right)=n+1,\Psi \left(v_3\right)=2n-1,\Psi \left(v_4\right)=2n-2,\Psi \left(v_5\right)=n,\Psi \left(v_{\alpha +3}\right)=\alpha$ , where $3\le \alpha \le n-3,\Psi \left(v_{\beta -2}\right)=\beta$ , where $n+3\le \beta \le 2n-3.$ We denote by $V\left(G^n\right)$ the vertex set of the graph $G^n$.

Fig. 8 CODC generating graph of $(2n-4)-$regular Circ$(2n;\{\{1,2,\dots ,n-1\}\setminus \{n-2\}\})$ by $G^n\cong$Butter fly $\cup$ $K_{1,2n-10}.$

Theorem 8

For all positive integers $n\ge 6$, there exists a CODC of $(2n-4)-$regular Circ $(2n;\{\{1,2,\dots ,n-1\}\setminus \{n-2\}\})$ by $G^n\cong$ Butterfly $\cup K_{1,2n-10}.$

Proof

The edges of length $1$ are $(\Psi \left(v_0\right),\Psi \left(v_3\right))$ and $(\Psi \left(v_4\right),\Psi \left(v_3\right));$ the edges of length $2$ are $(\Psi \left(v_0\right),\Psi \left(v_1\right))$ and $(\Psi \left(v_0\right),\Psi \left(v_4\right));$ the edges of length $l$ where $3\le l$ $\le n-3$ are $(\Psi \left(v_5\right),\Psi \left(v_{n-l+3}\right))$ and $(\Psi \left(v_5\right),\Psi \left(v_{l+n-2}\right));$ the edges of length $n-1$ are $(\Psi \left(v_2\right),\Psi \left(v_0\right))$ and$(\Psi \left(v_2\right),\Psi \left(v_1\right))$. Hence for every $l\in \{\{1,2,\dots ,n-1\}\setminus \{n-2\}\}$, $G^n$ contains exactly two edges of length $\{\{1,2,\dots ,n-1\}\setminus \{n-2\}\}$, and $\{r\left(l\right):l\in \{\{1,2,\dots ,n-1\}\setminus \{n-2\}\}\}=\{\{1,2,\dots ,n-1\}\setminus \{n-2\}\}$. Thus $G^n$ has an orthogonal labelling.   $\square$

A CODC generating graph of $12-$regular Circ $(16;\{1,2,3,4,5,7\})$ by $G^8\cong$Butterfly $\cup$ $K_{1,4}$, is shown in Fig. 9.

Fig. 9 CODC generating graph of $12-$regular Circ $(16;\{1,2,3,4,5,7\})$ by $G^8\cong$Butterfly $\cup$ $K_{1,4}.$

For the following Corollary, $E(G^n\setminus \{(\Psi \left(v_0\right),\Psi \left(v_1\right)),(\Psi \left(v_0\right),\Psi \left(v_4\right))\})=E(P_5\cup K_{1,2n-10})=\{(\Psi \left(v_2\right),\Psi \left(v_0\right)),(\Psi \left(v_2\right),\Psi \left(v_1\right)),(\Psi \left(v_0\right),\Psi \left(v_3\right)),(\Psi \left(v_4\right),\Psi \left(v_3\right))\}\cup \{(\Psi \left(v_5\right),\Psi \left(v_{\alpha +3}\right)):3\le \alpha \le n-3\}$ $\cup \{(\Psi \left(v_5\right),\Psi \left(v_{\beta -2}\right)):n+3\le \beta \le 2n-3\}$, where $\Psi :V(P_5\cup K_{1,2n-10})⟶{\mathbb{Z}}_{2n}$ is defined by $\Psi \left(v_0\right)=0,\Psi \left(v_1\right)=2,\Psi \left(v_2\right)=n+1,\Psi \left(v_3\right)=2n-1,\Psi \left(v_4\right)=2n-2,\Psi \left(v_5\right)=n,\Psi \left(v_{\alpha +3}\right)=\alpha$, where $3\le \alpha$ $\le n-3,\Psi \left(v_{\beta -2}\right)=\beta$, where $n+3\le \beta \le 2n-3.$

Corollary 9

For all positive integers $n\ge 6$, there exists a CODC of $(2n-6)-$regular Circ $(2n;\{\{1,3,4,\dots ,n-1\}\setminus \{n-2\}\})$ by $G^n\setminus \{(\Psi \left(v_0\right),\Psi \left(v_1\right)),(\Psi \left(v_0\right),\Psi \left(v_4\right))\}\cong P_5\cup K_{1,2n-10}.$

Proof

The edges of length $1$ are $(\Psi \left(v_0\right),\Psi \left(v_3\right))$ and $(\Psi \left(v_4\right),\Psi \left(v_3\right));$ the edges of length $l$ where $3\le l$ $\le n-3$ are $(\Psi \left(v_5\right),\Psi \left(v_{n-l+3}\right))$ and $(\Psi \left(v_5\right),\Psi \left(v_{l+n-2}\right));$ the edges of length $n-1$ are $(\Psi \left(v_2\right),\Psi \left(v_0\right))$ and$(\Psi \left(v_2\right),\Psi \left(v_1\right))$. Hence for every $l\in \{\{1,3,\dots ,n-1\}\setminus \{n-2\}\}$, $P_5\cup K_{1,2n-10}$ contains exactly two edges of length $\{\{1,3,\dots ,n-1\}\setminus \{n-2\}\}$, and $\{r\left(l\right):l\in \{\{1,3,\dots ,n-1\}\setminus \{n-2\}\}\}=\{\{1,3,\dots ,n-1\}\setminus \{n-2\}\}$. Thus $P_5\cup K_{1,2n-10}$ has an orthogonal labelling.   $\square$

A CODC generating graph of $10-$regular Circ $(16;\{1,3,4,5,7\})$ by $P_5\cup K_{1,6}$, is shown in Fig. 10.

Fig. 10 CODC generating graph of $10-$regular Circ $(16;\{1,3,4,5,7\})$ by $P_5\cup K_{1,6}.$

Notes

Peer review under responsibility of Kalasalingam University.