Randić index and information

Peer review under responsibility of Kalasalingam University.

Abstract

The Randić index $R\left(G\right)$ is one of the classical graph-based molecular structure descriptors that found countless applications in chemistry and pharmacology. The mathematical background of this index is also well elaborated. We now point out a hitherto unnoticed feature of $R\left(G\right)$, namely its connection with the degree-based information content of a (molecular) graph. This connection is based on the linear correlation between$R\left(G\right)$ and the logarithm of the multiplicative version of the Randić index.

Keywords:

• Randić index
• Information content of molecular graph
• Multiplicative Randić index

1 Introduction

The Randić index (also known under the name connectivity index) is a much investigated degree-based topological index [1–3^[1][2][3]]. It was invented in 1976 by Milan Randić [1] and is defined as (1.1) $R\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{1}{\sqrt{d\left(u\right)d\left(v\right)}}$(1.1) where the notation used is defined below. Among the several hundred presently existing graph-based molecular structure descriptors [4,5], the Randić index is certainly the most widely applied in chemistry and pharmacology, in particular for designing quantitative structure–property and structure–activity relations. Details of these applications can be found in the books [3,6,7] and the surveys written by Randić himself [8,9].

After a delay longer than 20 years, mathematicians recognized that the graph invariant $R\left(G\right)$ possesses a wealth of interesting and non-trivial mathematical properties [10,11]. This eventually resulted in extensive mathematical research along these lines and countless published papers; for details see [12,13] and the references quoted therein. Especially remarkable is the discovery of an algebraic connection between the Randić index and the normalized Laplacian matrix [14–16^[14][15][16]].

In the present paper, we point out a further, hitherto unnoticed, feature of the Randić index, namely its connection with the information content of the underlying molecular graph.

In order to achieve this goal, we need some preparations.

2 Graph-theoretical definitions and results

Let $G$ be a (molecular) graph [17,18] and let $V\left(G\right)$ and $E\left(G\right)$ be its vertex and edge sets, respectively. This graph is assumed to possess n vertices and m edges. If u and v are two adjacent vertices of the graph G, then the edge connecting them will be denoted by uv.

The degree $d\left(v\right)$ of the vertex v is the number of first neighbors of this vertex. According to a well known result of graph theory, (2.1) $\sum _{v\in V\left(G\right)}d\left(v\right)=2m.$(2.1)

The Randić index $R\left(G\right)$ of the (molecular) graph G is defined via Eq. (1.1(1.1) $R\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{1}{\sqrt{d\left(u\right)d\left(v\right)}}$(1.1) ). It is one of the several dozens of vertex-degree-based molecular structure descriptors of the general form $TI\left(G\right)=\sum _{uv\in E\left(G\right)}F\left(d\left(u\right),d\left(v\right)\right)$that have been and are being considered in contemporary mathematical chemistry and chemometrics; for details see [2,4,5].

Some time ago, Todeschini and Consonni [19] proposed to extend the area of degree-based molecular structure-descriptors by examining multiplicative topological indices of the form (2.2) $MTI\left(G\right)=\prod _{uv\in V\left(G\right)}F\left(d\left(u\right),d\left(v\right)\right)$(2.2) where $\prod$ indicates the product of the terms $F\left(d\left(u\right),d\left(v\right)\right)$. The first such topological index studied was the multiplicative version of the Wiener index [20–22^[20][21][22]]. Recently, the multiplicative Zagreb indices attracted much attention [23–26^{[23][24][25][26]}]. To the present authors’ best knowledge, the multiplicative Randić index has not been considered until now.

Bearing in mind Eqs. (1.1(1.1) $R\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{1}{\sqrt{d\left(u\right)d\left(v\right)}}$(1.1) ) and (2.2(2.2) $MTI\left(G\right)=\prod _{uv\in V\left(G\right)}F\left(d\left(u\right),d\left(v\right)\right)$(2.2) ), we may define the multiplicative Randić index as (2.3) $MR\left(G\right)=\prod _{uv\in E\left(G\right)}\frac{1}{\sqrt{d\left(u\right)d\left(v\right)}}.$(2.3)

Since any vertex $v\in V\left(G\right)$ is adjacent to exactly $d\left(v\right)$ other vertices, in the product on the right-hand side of Eq. (2.3(2.3) $MR\left(G\right)=\prod _{uv\in E\left(G\right)}\frac{1}{\sqrt{d\left(u\right)d\left(v\right)}}.$(2.3) ), each term $d\left(v\right)$appears $d\left(v\right)$ times. This yields:

Theorem 2.1

$MR\left(G\right)=\prod _{v\in V\left(G\right)}\frac{1}{\sqrt{d{\left(v\right)}^{d\left(v\right)}}}={\left(\prod _{v\in V\left(G\right)}d{\left(v\right)}^{d\left(v\right)}\right)}^{-1∕2}$

i.e., (2.4) $logMR\left(G\right)=-\frac{1}{2}\sum _{v\in V\left(G\right)}d\left(v\right)logd\left(v\right).$(2.4)

At this point, we have to recall that the information content of a system for which a probability distribution $\left(p_1,p_2,\dots ,p_n\right)$ holds, is equal to [27,28] (2.5) $I=-\sum _{i=1}^n{p}_i{log}_2{p}_i.$(2.5)

As usual, in Eq. (2.5(2.5) $I=-\sum _{i=1}^n{p}_i{log}_2{p}_i.$(2.5) ), the conditions $p_i\ge 0,i=1,2,\dots ,n$ and $p_1+p_2+\cdots +p_n=1$ are assumed to be obeyed. Applying formula (2.5(2.5) $I=-\sum _{i=1}^n{p}_i{log}_2{p}_i.$(2.5) ) to molecules and molecular graphs, it was possible to conceive a variety of chemically relevant information contents of chemical compounds [28]. In view of the obvious formal analogy between Eqs. (2.4(2.4) $logMR\left(G\right)=-\frac{1}{2}\sum _{v\in V\left(G\right)}d\left(v\right)logd\left(v\right).$(2.4) ) and (2.5(2.5) $I=-\sum _{i=1}^n{p}_i{log}_2{p}_i.$(2.5) ), we may think of a vertex-degree-based information content of the (molecular) graph G.

In order to obey the basic requirements behind formula (2.5(2.5) $I=-\sum _{i=1}^n{p}_i{log}_2{p}_i.$(2.5) ), introduce the auxiliary quantities $\delta \left(v\right)=\frac{d\left(v\right)}{2m},v\in V\left(G\right)$which, according to Eq. (2.1(2.1) $\sum _{v\in V\left(G\right)}d\left(v\right)=2m.$(2.1) ), satisfy the necessary conditions $\delta \left(v\right)\ge 0,v\in V\left(G\right)$ and ${\sum }_{v\in V\left(G\right)}\delta \left(v\right)=1$. Then the vertex-degree-based information content of the graph G is $I\left(G\right)=-\sum _{v\in V\left(G\right)}\delta \left(v\right){log}_2\delta \left(v\right)=-\sum _{v\in V\left(G\right)}\frac{d\left(v\right)}{2m}{log}_2\frac{d\left(v\right)}{2m}.$Eq. (2.4(2.4) $logMR\left(G\right)=-\frac{1}{2}\sum _{v\in V\left(G\right)}d\left(v\right)logd\left(v\right).$(2.4) ) can now be rewritten as: ${log}_{2}MR=-\frac{1}{2}\sum _{v\in V\left(G\right)}2m\delta \left(v\right){log}_2\left[2m\delta \left(v\right)\right]$ $=-m\sum _{v\in V\left(G\right)}\delta \left(v\right){log}_2\delta \left(v\right)-m{log}_2\left(2m\right)\sum _{v\in V\left(G\right)}\delta \left(v\right)$ $=mI\left(G\right)-m{log}_2\left(2m\right)$ which implies our final result:

Theorem 2.2

Let $G$ be a graph with $m$ edges. The vertex-degree-based information content of $G$ and the multiplicative Randić index $MR\left(G\right)$ are related as: (2.6) $I\left(G\right)=\frac{1}{m}{log}_{2}MR\left(G\right)-{log}_2\left(2m\right).$(2.6)

3 The Randić index connection

Theorem 2.2 is a straightforward consequence of the definition (2.3(2.3) $MR\left(G\right)=\prod _{uv\in E\left(G\right)}\frac{1}{\sqrt{d\left(u\right)d\left(v\right)}}.$(2.3) ) of the multiplicative Randić index. It, however, does not connect the ordinary Randić index, Eq. (1.1(1.1) $R\left(G\right)=\sum _{uv\in E\left(G\right)}\frac{1}{\sqrt{d\left(u\right)d\left(v\right)}}$(1.1) ), with any information content of the (molecular) graph G. In order to arrive at such a connection, we have to establish a relation between $R\left(G\right)$ and $MR\left(G\right)$.

Within the earlier studies of the multiplicative Wiener index [20,21], it was discovered that there exists an excellent linear correlation between the logarithm of the multiplicative Wiener index and the ordinary Wiener index. Such correlations were found to hold for various classes of molecular graphs of isomeric compounds. Bearing this in mind, the obvious property that had to be checked is whether analogous correlations exist also between $logMR\left(G\right)$ and $R\left(G\right)$. By means of an extensive numerical work we confirmed that, indeed, such a correlation does exist, i.e., that within classes of molecular graphs with fixed values of the parameters n and m, the equality (3.1) $logMR\left(G\right)=a\cdot R\left(G\right)+b$(3.1) holds as a fairly accurate approximation, with a and b being empirically determined constants (depending on n and m). If relation (3.1(3.1) $logMR\left(G\right)=a\cdot R\left(G\right)+b$(3.1) ) is substituted back into (2.6(2.6) $I\left(G\right)=\frac{1}{m}{log}_{2}MR\left(G\right)-{log}_2\left(2m\right).$(2.6) ), then the information content $I\left(G\right)$becomes dependent on the Randić index in a simple, linear manner: (3.2) $I\left(G\right)=A\cdot R\left(G\right)+B$(3.2) where A and B are empirically determined constants, depending on n and m. Details of our numerical tests of relation (3.2(3.2) $I\left(G\right)=A\cdot R\left(G\right)+B$(3.2) ) are described in the subsequent section.

4 Numerical work

The quality of the approximation given by Eq. (3.2(3.2) $I\left(G\right)=A\cdot R\left(G\right)+B$(3.2) ) was tested on chemical trees from 8 to 20 vertices, as well as on unicyclic, bicyclic, …, pentacyclic 10-vertex connected chemical graphs. These data were generated using the Open Molecule Generator [29]. It creates data as sdf-files. An in-house Python program was developed for the calculation of vertex-degree-based information content of a graph, Randić index and statistical parameters that show an extent of correlation between these topological indices. The Open Babel module [30] has been used for reading sdf-files and generating adjacency matrices from alkanes.

The obtained statistical parameters for chemical trees are collected in Table 1. Correlation coefficient is approximately 0.95 and its value decreases by increasing the order of chemical trees. Standard error of estimate is decreasing in the same manner.

Table 1 Slope, intercept, correlation coefficient and standard error of the estimate (3.2(3.2) $I\left(G\right)=A\cdot R\left(G\right)+B$(3.2) ) for chemical trees from 8 to 20 vertices.

# C-atoms	# molecules	Slope	Intercept	$R$	SEE
8	18	0.406	1.347	0.975	0.0229
9	35	0.354	1.543	0.963	0.0173
10	75	0.324	1.670	0.962	0.0108
11	159	0.296	1.798	0.959	0.0070
12	355	0.271	1.921	0.955	0.0045
13	802	0.251	2.036	0.953	0.0028
14	1 858	0.233	2.139	0.951	0.0018
15	4 347	0.218	2.237	0.949	0.0011
16	10 359	0.204	2.329	0.948	0.0007
17	24 894	0.192	2.415	0.946	0.0004
18	60 523	0.182	2.496	0.945	0.0003
19	148 284	0.172	2.573	0.944	0.0002
20	366 319	0.164	2.647	0.944	0.0001

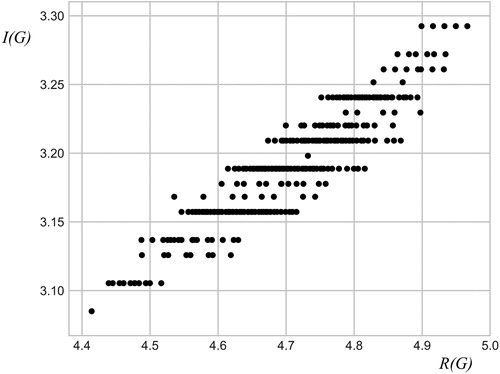
An illustration of linear correlation between I (G) and R (G) in the case of chemical trees is given in Fig. 1.

Fig. 1 Linear correlation between vertex-degree-based information content of graphs and Randić index for chemical trees with eleven vertices.

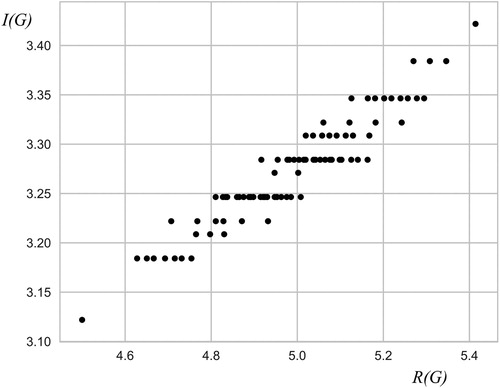
Further investigation of the dependence between I (G) and R (G) was extended also to connected chemical graphs containing cycles. In this study, 10-vertex chemical graphs having up to 5 cycles were considered. Linear correlation between the vertex-degree-based information content of a graph and Randić index has also been confirmed. The correlation coefficient is approximately 0.94. The standard error of the estimate (3.2(3.2) $I\left(G\right)=A\cdot R\left(G\right)+B$(3.2) ) is decreasing with the number of cycles. The results obtained are summarized in Table 2.

Table 2 Slope, intercept, correlation coefficient and standard error of the estimate (3.2(3.2) $I\left(G\right)=A\cdot R\left(G\right)+B$(3.2) ) for ten-vertex connected chemical graph having up to 5 cycles.

# cycles	# molecules	Slope	Intercept	$R$	SEE
1	475	0.336	1.609	0.947	0.0052
2	1591	0.344	1.574	0.941	0.0031
3	3629	0.353	1.532	0.938	0.0022
4	6100	0.362	1.493	0.937	0.0017
5	7738	0.372	1.447	0.940	0.0015

A pictorial example of the quality of linear correlation between I (G) and R (G) in the case of 10-vertex cyclic connected chemical graphs is given in Fig. 2.

Fig. 2 Dependence of vertex-degree-based information content of a graph on Randić index in the case of tricyclic 10-vertex connected chemical graphs.

5 Discussion and concluding remarks

Numerical investigation of linear dependence between vertex-degree-based information content of a graph and Randić index has been demonstrated in all conducted numerical experiments. The quality of the correlation is quantified by Pearson correlation coefficient and standard error of an estimate. Results presented in Tables 1 and 2 indicate a reasonably good linear correlation.

However, further inspection of the plotted data (see Figs. 1 and 2) reveals data-clustering onto several horizontal lines. This indicates that I (G) (contrary to R (G)) carries information only on degree distribution in graphs and not on their mutual interplay. The insensitivity of vertex-degree-based information of a graph on subtle structural differences among graphs reduces its application potential in chemistry.

Notes

Peer review under responsibility of Kalasalingam University.