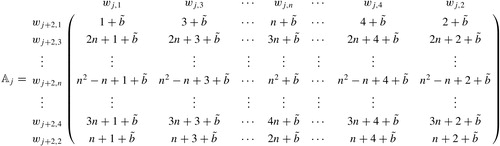Lexicographic product graphs Pm[Pn] are antimagic

Peer review under responsibility of Kalasalingam University.

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11401430 and 11301381).

Abstract

A graph with $q$ edges is called $antimagic$ if its edges can be labeled with 1, 2, $\dots$, $q$ such that the sums of the labels on the edges incident to each vertex are distinct. Hartsfield and Ringel conjectured that every connected graph other than $K_2$ is antimagic. In this paper, through a labeling method and a modification on this labeling, we obtained that the lexicographic product graphs $P_m\left[P_n\right]$ are antimagic.

Keywords:

• Antimagic graph
• Lexicographic product
• Path

1 Introduction

Graphs considered here are all simple, connected, finite and undirected. A path with $k$ vertices is called a $k$-path and denoted by $P_k$, $K_{r,s}$ denotes the complete bipartite graph with the two partite sets sizes $r$ and $s$ respectively. Given a graph $G=(V,E)$, a graph labeling is a bijective mapping $\varphi$ : $E\to \{1,2,\dots ,\left|E\right|\}$. For each vertex $u$ of $G$, the vertex-sum $f_{\varphi }\left(u\right)$ at $u$ is defined as $f_{\varphi }\left(u\right)={\sum }_{e\in E\left(u\right)}\varphi \left(e\right)$, where $E\left(u\right)$ is the set of edges incident to $u$. In 1990, Hartsfield and Ringel [1] introduced the definition of antimagic graph, which states that a graph is called antimagic if there is a graph labeling $\varphi$ such that $f_{\varphi }\left(u\right)\ne f_{\varphi }\left(v\right)$ for any two distinct vertices $u$, $v$ $\in V\left(G\right)$. They also proposed the following conjecture.

Conjecture

[1]

Every connected graph other than $K_2$ is antimagic.

Since then, the conjecture has received much attention, and many interesting results are obtained. For dense graphs, Alon, Kaplan, Lev, Roditty and Yuster in [2] obtained that there is an absolute constant $c$ such that graphs with minimum degree $\delta \left(G\right)\ge c$log$\left|V\left(G\right)\right|$ are anti-magic. In addition, graphs with maximum degree $▵\left(G\right)\ge \left|V\left(G\right)\right|-2$ are antimagic. For sparse graphs, Chang, Liang, Pan and Zhu [3] proved that regular graphs are antimagic. The antimagicness of regular graphs has also been obtained by K. Bérczi, A. Bernáth and M. Vizer [4] independently. In addition, the antimagicness concerning trees [5,6], Cartesian product of graphs [7], join graphs [8,9], generalized pyramid graphs [10], directed graphs [11], etc., have been proved. Recently, S. Arumugam, K. Premalatha and M. Bača introduced the local antimagic labeling of graphs [12]. For more information about the antimagic graphs, a survey paper by Gallian [13] is referred.

For $n\ge 3$, a generalized magic matrix is an $n\times n$ matrix consisting of the distinct positive integers from 1 to $n^2$ such that the sum of the elements in each of its rows, each of its columns all equal the same number. The following lemma will be useful in the present paper.

Lemma 1

[14]

For $n\ge 3$, there is an $n\times n$ generalized magic matrix.

The lexicographic product or graph composition $G\left[H\right]$ of graphs $G$ and $H$ is a graph such that the vertex set of $G\left[H\right]$ is the Cartesian product $V\left(G\right)\times V\left(H\right)$, and any two vertices $(u,v)$ and $(x,y)$ are adjacent in $G\left[H\right]$ if and only if either $u$ is adjacent with $x$ in $G$ or $u=x$ and $v$ is adjacent with $y$ in $H$. This is equivalent to replacing each vertex of $G$ by a copy of $H$, and linking these copies by complete bipartite graphs according to the edges of $G$. In general, the lexicographic product is noncommutative: $G\left[H\right]\ne H\left[G\right]$. Fig. 1 is the graph $P_4\left[P_5\right]$ as an example. Terminologies and notations not defined here can be found in [15] for graph theory in general.

Fig. 1 $P_4,P_5$, and $P_4\left[P_5\right]$.

Although the antimagicness of graphs concerning Cartesian product has been explored extensively, there are few results regarding lexicographic product. As far as we know, the only result concerning lexicographic product of graphs is obtained by Wang and Hsiao in [7], which states that

Lemma 2

[7]

If $H$ is an antimagic $d$-regular graph with $d>1$, then the lexicographic product graph $G\left[H\right]$ is antimagic.

Notice that the antimagicness of regular graphs has been obtained in [3] and [4] respectively. So, the result in Lemma 2 can be extended as

Lemma 3

If $H$ is a $d$-regular graph with $d>1$, then the lexicographic product graph $G\left[H\right]$ is antimagic.

But, except for Lemma 3, there are no other results concerning the antimagicness of lexicographic product of graphs. In this paper, we obtained the following result concerning the antimagicness of the lexicographic product of graphs.

Theorem 1

The lexicographic product graphs $P_m\left[P_n\right]$ are antimagic.

2 The labeling technique for $P_m\left[P_n\right]$ ($m,n\ge 3$)

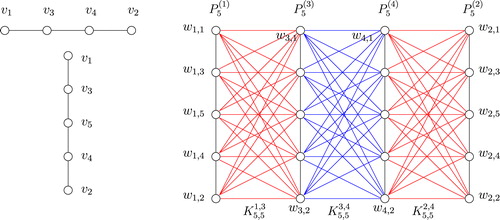
For convenience, throughout this paper, a $n$-path $P_n$ is represented by a specified sequence $v_1{v}_3{v}_5\cdots v_n\cdots v_6{v}_4{v}_2$ of its vertices, i.e., $P_n=v_1{v}_3{v}_5\cdots v_n\cdots v_6{v}_4{v}_2$. In graph $P_m\left[P_n\right]$, the vertices are represented by $w_{j,1}$, $w_{j,2}$, $\dots$, $w_{j,n}$ ($1\le j\le m$). For each $j\in \{1,2,\dots ,m\}$, the vertex set $\{w_{j,1},w_{j,2},\dots ,w_{j,n}\}$ is called the $V_j$-$set$ of $P_m\left[P_n\right]$. In $V_j$, the vertices $w_{j,1}$ and $w_{j,2}$ are called the endpoints of $V_j$, and the other vertices are called the internal vertices of $V_j$. The graph $P_m\left[P_n\right]$ can be decomposed into $m$ copies of the path $P_n$ and $m-1$ copies of the complete bipartite graphs $K_{n,n}$. The $m$ copies of the path $P_n$ are denoted by $P_n^{\left(1\right)}$, $P_n^{\left(2\right)}$, $\dots$ and $P_n^{\left(m\right)}$, where $P_n^{\left(j\right)}=w_{j,1}{w}_{j,3}\cdots w_{j,n}\cdots w_{j,4}{w}_{j,2}$ for $1\le j\le m$. The $m-1$ copies of the complete bipartite graph $K_{n,n}$ are represented by $K_{n,n}^{j,j+2}$ ($1\le j\le m-2$) and $K_{n,n}^{m-1,m}$ respectively, where the symbol $K_{n,n}^{r,s}$ stands for the complete bipartite graph between $P_n^{\left(r\right)}$ and $P_n^{\left(s\right)}$ in $P_m\left[P_n\right]$. 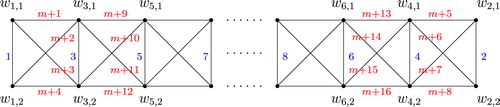The symbols mentioned above can be deduced from an example in Fig. 1.

Let $\varphi ={\varphi }_1+{\varphi }_2$ be a graph labeling on $P_m\left[P_n\right]$, where ${\varphi }_1:\{E\left(P_n^{\left(1\right)}\right)\cup E\left(P_n^{\left(2\right)}\right)\cup \cdots \cup E\left(P_n^{\left(m\right)}\right)\}\to \{1,2,\dots ,m(n-1)\}$is a labeling on the subgraph ${\bigcup }_{k=1}^m{P}_n^{\left(k\right)}$ of $P_m\left[P_n\right]$, and $\begin{array}{cc}\hfill {\varphi }_2:& \{E\left(K_{n,n}^{1,3}\right)\cup E\left(K_{n,n}^{3,5}\right)\cup \cdots \cup E\left(K_{n,n}^{m-1,m}\right)\cup \cdots \cup E\left(K_{n,n}^{4,6}\right)\cup E\left(K_{n,n}^{2,4}\right)\}\hfill \\ \hfill & \to \{m(n-1)+1,m(n-1)+2,\dots ,m(n-1)+(m-1)n^2\}\hfill \end{array}$is a labeling on the subgraph $\left({\bigcup }_{j=1}^{m-2}{K}_{n,n}^{j,j+2}\right)\bigcup K_{n,n}^{m-1,m}$ of $P_m\left[P_n\right]$. The following is the technique for graph labeling $\varphi ={\varphi }_1+{\varphi }_2$ on $P_m\left[P_n\right]$.

Step 1. The graph labeling ${\varphi }_1$ on the paths $P_n^{\left(1\right)}$, $P_n^{\left(2\right)}$, $\dots$ and $P_n^{\left(m\right)}$ in $P_m\left[P_n\right]$.

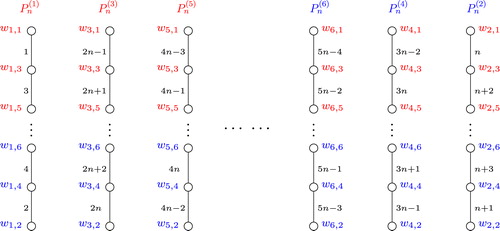
For $j=1,2,\dots ,m$, the vertex set of $P_n^{\left(j\right)}$ is $\{w_{j,1},w_{j,3},\dots ,w_{j,n},\dots ,w_{j,4},w_{j,2}\}$, and the edge set of $P_n^{\left(j\right)}$ is $\left\{(w_{j,i},w_{j,i+2})\right|i=1,2,\dots ,n-2\}\cup (w_{j,n-1},w_{j,n})$, which is illustrated by Fig. 2. The graph labeling ${\varphi }_1$ on the edges of $P_n^{\left(j\right)}$ is defined as follows. (1) $\left\{\begin{array}{cc}\hfill & {\varphi }_1(w_{j,i},w_{j,i+2})=i+(j-1)(n-1),i\in \{1,2,\dots ,n-2\}\hfill \\ \hfill & {\varphi }_1(w_{j,n-1},w_{j,n})=(n-1)+(j-1)(n-1).\hfill \end{array}\right.$(1) Therefore, for $1\le j\le m$, we have $f_{{\varphi }_1}\left(w_{j,i}\right)=\left\{\begin{array}{cc}i+(j-1)(n-1),\hfill & i=1,2\hfill \\ 2(j-1)(n-1)+2i-2,\hfill & i=3,\dots ,n-1\hfill \\ 2n-3+2(j-1)(n-1),\hfill & i=n.\hfill \end{array}\right.$Furthermore, the following monotonic sequences can be deduced from a simple calculation

$f_{{\varphi }_1}\left(w_{j,1}\right)<f_{{\varphi }_1}\left(w_{j,2}\right)<\cdots <f_{{\varphi }_1}\left(w_{j,n}\right),j=1,2,\dots ,m.$

Fig. 2 Labeling ${\varphi }_1$ on edges of $P_n^{\left(j\right)}$.

Step 2. The graph labeling ${\varphi }_2$ on the complete bipartite graphs $K_{n,n}^{1,3}$, $K_{n,n}^{3,5}$, $\dots$, $K_{n,n}^{m-1,m}$, $\dots$, $K_{n,n}^{4,6}$, $K_{n,n}^{2,4}$ in $P_m\left[P_n\right]$.

When Step 1 is completed, we have labeled all the edges in $P_n^{\left(1\right)}$, $P_n^{\left(2\right)}$, $\dots$ and $P_n^{\left(m\right)}$, and used all the numbers in the set $\{1,2,\dots ,m(n-1)\}$. In the following, the edge labeling for $K_{n,n}^{j,j+2}$ ($1\le j\le m-2$) is represented in Step 2-1, and the edge labeling for $K_{n,n}^{m-1,m}$ is represented in Step 2-2.

(2-1) For $1\le j\le m-2$, the graph labeling ${\varphi }_2$ on $K_{n,n}^{j,j+2}$ is represented by the matrix ${\mathbb{A}}_j$, and the entry $a{\left(j\right)}_{r,s}$, which lies in the $r$th row and $s$th column of ${\mathbb{A}}_j$, represents the number labeled on the edge $(w_{j+2,r},w_{j,s})$ through ${\varphi }_2$. The matrix ${\mathbb{A}}_j$ is defined as (2) ${\mathbb{A}}_j=(m(n-1)+(j-1)n^2)\cdot {\mathbb{E}}_n+\mathbb{A},j=1,2,\dots ,m-2$(2) where ${\mathbb{E}}_n$ is an $n\times n$ matrix with all entries being 1, and $\mathbb{A}$ is the following matrix $\mathbb{A}=\left(\begin{array}{ccccccc}\hfill 1\hfill & \hfill 3\hfill & \hfill \cdots \hfill & \hfill n\hfill & \hfill \cdots \hfill & \hfill 4\hfill & \hfill 2\hfill \\ \hfill 2n+1\hfill & \hfill 2n+3\hfill & \hfill \cdots \hfill & \hfill 3n\hfill & \hfill \cdots \hfill & \hfill 2n+4\hfill & \hfill 2n+2\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill n^2-n+1\hfill & \hfill n^2-n+3\hfill & \hfill \cdots \hfill & \hfill n^2\hfill & \hfill \cdots \hfill & \hfill n^2-n+4\hfill & \hfill n^2-n+2\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 3n+1\hfill & \hfill 3n+3\hfill & \hfill \cdots \hfill & \hfill 4n\hfill & \hfill \cdots \hfill & \hfill 3n+4\hfill & \hfill 3n+2\hfill \\ \hfill n+1\hfill & \hfill n+3\hfill & \hfill \cdots \hfill & \hfill 2n\hfill & \hfill \cdots \hfill & \hfill n+4\hfill & \hfill n+2\hfill \end{array}\right).$For more intuitive, ${\mathbb{A}}_j$ may be represented as the following, where $\tilde{b}=m(n-1)+(j-1)n^2$.

(2-2) When Step 1 and Step 2-1 are completed, all the numbers in the set {1, 2, $\dots$, $m(n-1)+(m-2)n^2$} have been used. The graph labeling ${\varphi }_2$ on $K_{n,n}^{m-1,m}$ is represented by the following matrix ${\mathbb{A}}_{m-1}$. (3) ${\mathbb{A}}_{m-1}=(m(n-1)+(m-2)n^2)\cdot {\mathbb{E}}_n+\mathbb{M},$(3) where $\mathbb{M}$ is a $n\times n$ generalized magic matrix according to Lemma 1. The entry $b_{r,s}$, which lies in the $r$th row and $s$th column of ${\mathbb{A}}_{m-1}$, indicates the number labeled on the edge $(w_{m,r},w_{m-1,s})$ through ${\varphi }_2$.

For $1\le k\le m-1$, let $R_k\left(r\right)$ denote the sum of the elements in row $r$ of ${\mathbb{A}}_k$, $C_k\left(s\right)$ denote the sum of the elements in column $s$ of ${\mathbb{A}}_k$. Then $f_{{\varphi }_2}\left(w_{j,i}\right)$ can be represented as $f_{{\varphi }_2}\left(w_{j,i}\right)=\left\{\begin{array}{cccc}\hfill & C_j\left(i\right)=(j-\frac{1}{2})n^3+(m-\frac{1}{2})n^2+(i-m)n,\hfill & \hfill & j=1,2\hfill \\ \hfill & R_{j-2}\left(i\right)+C_j\left(i\right)=(2j-\frac{7}{2})n^3+(2m+i-1)n^2+(\frac{1}{2}+i-2m)n,\hfill & \hfill & j=3,4,\dots ,m-2\hfill \\ \hfill & R_{m-3}\left(i\right)+C_{m-1}\left(i\right)=(2m-\frac{11}{2})n^3+(2m+i-\frac{1}{2})n^2+(1-2m)n,\hfill & \hfill & j=m-1\hfill \\ \hfill & R_{m-1}\left(i\right)+R_{m-2}\left(i\right)=(2m-\frac{9}{2})n^3+(2m+i-\frac{1}{2})n^2+(1-2m)n,\hfill & \hfill & j=m.\hfill \end{array}\right.$

Through the above discussion we can get that, for each vertex $w_{j,i}$ of $P_m\left[P_n\right]$, the vertex-sum $f_{\varphi }\left(w_{j,i}\right)=f_{{\varphi }_1}\left(w_{j,i}\right)+f_{{\varphi }_2}\left(w_{j,i}\right)$ has the following expression $\begin{array}{c}\hfill f_{\varphi }\left(w_{j,i}\right)=\left\{\begin{array}{cccc}\hfill & (j-\frac{1}{2})n^3+(m-\frac{1}{2})n^2+(i+j-m-1)n+i-j+1,\hfill & \hfill & j=1,2;i=1,2\hfill \\ \hfill & (j-\frac{1}{2})n^3+(m-\frac{1}{2})n^2+(i+2j-m-2)n+2i-2j,\hfill & \hfill & j=1,2;3\le i\le n-1\hfill \\ \hfill & (j-\frac{1}{2})n^3+(m+\frac{1}{2})n^2+(2j-m)n-2j-1,\hfill & \hfill & j=1,2;i=n\hfill \\ \hfill & (2j-\frac{7}{2})n^3+(2m+i-1)n^2+(i+j-2m-\frac{1}{2})n+i-j+1,\hfill & \hfill & 3\le j\le m-2;i=1,2\hfill \\ \hfill & (2j-\frac{7}{2})n^3+(2m+i-1)n^2+(i+2j-2m-\frac{3}{2})n+2i-2j,\hfill & \hfill & 3\le j\le m-2;3\le i\le n-1\hfill \\ \hfill & (2j-\frac{5}{2})n^3+2m{n}^2+(2j-2m+\frac{1}{2})n-2j-1,\hfill & \hfill & 3\le j\le m-2;i=n\hfill \\ \hfill & (2m-\frac{11}{2})n^3+(2m+i-\frac{1}{2})n^2-(m+1)n+i-m+2,\hfill & \hfill & j=m-1;i=1,2\hfill \\ \hfill & (2m-\frac{11}{2})n^3+(2m+i-\frac{1}{2})n^2-3n+2i-2m+2,\hfill & \hfill & j=m-1;3\le i\le n-1\hfill \\ \hfill & (2m-\frac{11}{2})n^3+(2m+n-\frac{1}{2})n^2-n-2m+1,\hfill & \hfill & j=m-1;i=n\hfill \\ \hfill & (2m-\frac{9}{2})n^3+(2m+i-\frac{1}{2})n^2-mn+i-m+1,\hfill & \hfill & j=m;i=1,2\hfill \\ \hfill & (2m-\frac{9}{2})n^3+(2m+i-\frac{1}{2})n^2-n+2i-2m,\hfill & \hfill & j=m;3\le i\le n-1\hfill \\ \hfill & (2m-\frac{9}{2})n^3+(2m+n-\frac{1}{2})n^2+n-2m-1,\hfill & \hfill & j=m;i=n.\hfill \end{array}\right.\end{array}$

The following monotonic sequence can be deduced from a simple calculation.

Claim 1

For $1\le j\le m$, the vertex-sum of $w_{j,1}$, $w_{j,2}$, $\dots$, and $w_{j,n}$ in $P_m\left[P_n\right]$ satisfies (4) $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{j,1}\right)<f_{\varphi }\left(w_{j,2}\right)<f_{\varphi }\left(w_{j,3}\right)<\cdots <f_{\varphi }\left(w_{j,n-1}\right)<f_{\varphi }\left(w_{j,n}\right)\hfill \end{array}$(4)

Furthermore, we have the following claims.

Claim 2

The vertex-sums of all the endpoints in $P_m\left[P_n\right]$ satisfy (5) $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)<\cdots <f_{\varphi }\left(w_{j,1}\right)<f_{\varphi }\left(w_{j,2}\right)\hfill \\ \hfill & <\cdots <f_{\varphi }\left(w_{m-1,1}\right)<f_{\varphi }\left(w_{m-1,2}\right)<f_{\varphi }\left(w_{m,1}\right)<f_{\varphi }\left(w_{m,2}\right).\hfill \end{array}$(5)

Proof

According to Claim 1, it can be obtained that $f_{\varphi }\left(w_{j,1}\right)<f_{\varphi }\left(w_{j,2}\right)$ for $j=1,2,\dots ,m$. For $n\ge 2$, through the following calculations we can get the inequalities $f_{\varphi }\left(w_{j,2}\right)<f_{\varphi }\left(w_{j+1,1}\right)$ for $j=1,2,\dots ,m-1$. And thereforeClaim 2 is obtained. $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{2,1}\right)-f_{\varphi }\left(w_{1,2}\right)=n^3-2>0\hfill \\ \hfill & f_{\varphi }\left(w_{3,1}\right)-f_{\varphi }\left(w_{2,2}\right)=n^3+(m+\frac{1}{2})n^2+(\frac{1}{2}-m)n-2>0\hfill \\ \hfill & f_{\varphi }\left(w_{j+1,1}\right)-f_{\varphi }\left(w_{j,2}\right)=2n^3-n^2-2>0,j=3,4,\dots ,m-3\hfill \\ \hfill & f_{\varphi }\left(w_{m-1,1}\right)-f_{\varphi }\left(w_{m-2,2}\right)=2n^3-\frac{1}{2}{n}^2-\frac{1}{2}n-2>0\hfill \\ \hfill & f_{\varphi }\left(w_{m,1}\right)-f_{\varphi }\left(w_{m-1,2}\right)=n^3-n^2+n-2>0\square \hfill \end{array}$

Claim 3

The vertex-sums of all the internal vertices in $P_m\left[P_n\right]$ satisfy (6) $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,3}\right)<f_{\varphi }\left(w_{1,4}\right)<\cdots <f_{\varphi }\left(w_{1,n}\right)\hfill \\ \hfill & <f_{\varphi }\left(w_{2,3}\right)<f_{\varphi }\left(w_{2,4}\right)<\cdots <f_{\varphi }\left(w_{2,n}\right)<\hfill \\ \hfill & \cdots \cdots \cdots \cdots \hfill \\ \hfill & <f_{\varphi }\left(w_{m-1,3}\right)<f_{\varphi }\left(w_{m-1,4}\right)<\cdots <f_{\varphi }\left(w_{m-1,n}\right)\hfill \\ \hfill & <f_{\varphi }\left(w_{m,3}\right)<f_{\varphi }\left(w_{m,4}\right)<\cdots <f_{\varphi }\left(w_{m,n}\right).\hfill \end{array}$(6)

Proof

From Claim 1 we can get that $f_{\varphi }\left(w_{j,3}\right)<f_{\varphi }\left(w_{j,4}\right)<\cdots <f_{\varphi }\left(w_{j,n}\right)$ for $j=1,2,\dots ,m$. In the following, we will prove the inequality $f_{\varphi }\left(w_{j,n}\right)<f_{\varphi }\left(w_{j+1,3}\right)$. $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{2,3}\right)-f_{\varphi }\left(w_{1,n}\right)=n^3-n^2+3n+5>0\hfill \\ \hfill & f_{\varphi }\left(w_{3,3}\right)-f_{\varphi }\left(w_{2,n}\right)=n^3+(m+\frac{3}{2})n^2+(\frac{7}{2}-m)n+5>0\hfill \\ \hfill & f_{\varphi }\left(w_{j+1,3}\right)-f_{\varphi }\left(w_{j,n}\right)=n^3+2n^2+3n+5>0,j=3,4,\dots ,m-3\hfill \\ \hfill & f_{\varphi }\left(w_{m-1,3}\right)-f_{\varphi }\left(w_{m-2,n}\right)=n^3+\frac{5}{2}{n}^2+\frac{n}{2}+5>0\hfill \\ \hfill & f_{\varphi }\left(w_{m,3}\right)-f_{\varphi }\left(w_{m-1,n}\right)=3n^2+5>0.\hfill \end{array}$

From the above, we can get that Claim 3 is obtained.

Claim 4

Under the labeling $\varphi$, if there are two vertices in $P_m\left[P_n\right]$ whose vertex-sums are equal, then these two vertices must satisfy the property that one is an internal vertex of $V_{j_1}$ and the other is an endpoint of $V_{j_2}$ with $3\le j_1<j_2$.

Proof

(i) Firstly, we prove that $j_1<j_2$.

From Claims 2 and 3 we can get that the vertex-sums of all endpoints in $P_m\left[P_n\right]$ are pairwise distinct, and that the vertex-sums of all internal vertices in $P_m\left[P_n\right]$ are also pairwise distinct. So, the two vertices with the same vertex-sum must be that one is an internal vertex of $V_{j_1}$ and the other is an endpoint of $V_{j_2}$. Furthermore, combiningClaims 1 and 2 we can get that $j_1<j_2$.

(ii) Secondly, we prove that $3\le j_1$.

Without loss of generality, we may let $f_{\varphi }\left(w_{j_1,r}\right)=f_{\varphi }\left(w_{j_2,s}\right)$, where $w_{j_1,r}$ is one of the internal vertex of $V_{j_1}$, $w_{j_2,s}$ is one of the endpoint of $V_{j_2}$, $j_1,j_2\in \{1,2,\dots ,m\}$. Through a calculation we can get that $f_{\varphi }\left(w_{2,n}\right)<f_{\varphi }\left(w_{3,1}\right)$. So, from Claim 2 we can get that the following inequality holds for any $k>3$. $f_{\varphi }\left(w_{2,n}\right)<f_{\varphi }\left(w_{3,1}\right)<f_{\varphi }\left(w_{k,1}\right)<f_{\varphi }\left(w_{k,2}\right)$ Combining this inequality with Claim 3 it can be deduced that if $f_{\varphi }\left(w_{j_1,r}\right)=f_{\varphi }\left(w_{j_2,s}\right)$, then $3\le j_1$.

From Claim 4, the following proposition can be easily obtained.

Proposition

For $j_1<j_2$, if there is no internal vertex in $V_{j_1}$ whose vertex-sum is equal to that of an endpoint in $V_{j_2}$, then the vertex-sums of all vertices in $V_{j_1}$ and $V_{j_2}$ are pair distinct.

The difference between two vertex-sums is called the $footstep$ of the corresponding two vertices. Through some calculations, we can get the following claim.

Claim 5

(i) The footstep between two endpoints is (7) ${\theta }_1=f_{\varphi }\left(w_{j,2}\right)-f_{\varphi }\left(w_{j,1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}\hfill \end{array}\right.$(7) (8) ${\theta }_2=f_{\varphi }\left(w_{j,1}\right)-f_{\varphi }\left(w_{j-1,2}\right)=\left\{\begin{array}{cccc}\hfill & 2n^3-n^2-2,\hfill & \hfill & 4\le j\le m-2\hfill \\ \hfill & 2n^3-\frac{1}{2}{n}^2-\frac{1}{2}n-2,\hfill & \hfill & j=m-1\hfill \\ \hfill & n^3-n^2+n-2\hfill & \hfill & j=m.\hfill \end{array}\right.$(8)

(ii) For $4\le i\le n-1$, the footstep between two internal vertices is (9) ${\theta }_3=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+2,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+2,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.$(9)

(iii) For $i=n$, the footstep between two internal vertices is (10) $\begin{array}{cc}\hfill {\theta }_4=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=& f_{\varphi }\left(w_{j,n}\right)-f_{\varphi }\left(w_{j,n-1}\right)\hfill \\ \hfill =& \left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.\hfill \end{array}$(10)

Claim 6

Let $f_{\varphi }\left(w_{j_1,i_1}\right)=f_{\varphi }\left(w_{r_1,s_1}\right)$, $f_{\varphi }\left(w_{j_2,i_2}\right)=f_{\varphi }\left(w_{r_2,s_2}\right)$.

(i) If $j_1=j_2$, $i_1\ne i_2$ and $\{i_1,i_2\}\in \{1,2\}$, then $r_1=r_2$, $s_1\ne s_2$ and $\{s_1,s_2\}\in \{n-1,n\}$, i.e., if $w_{j_1,i_1}$ and $w_{j_2,i_2}$ are the two endpoints of $V_{j_1}$, then $w_{r_1,s_1}$ and $w_{r_2,s_2}$ must be the last two internal vertices of $V_{r_1}$. Furthermore, $r_1=r_2<j_1=j_2$.

(ii) If $j_1\ne j_2$, $r_1=r_2$, furthermore $w_{j_1,i_1}$ is one of the endpoints of $V_{j_1}$, $w_{j_2,i_2}$ is one of the endpoints of $V_{j_2}$, then $w_{r_1,s_1}$ and $w_{r_2,s_2}$ must be internal vertices of $V_{r_1}$ and they are separated by at least two other internal vertices of $V_{r_1}$.

Proof

Because $f_{\varphi }\left(w_{j_1,i_1}\right)=f_{\varphi }\left(w_{r_1,s_1}\right)$ and $f_{\varphi }\left(w_{j_2,i_2}\right)=f_{\varphi }\left(w_{r_2,s_2}\right)$, so we have (11) $f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)=f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right).$(11)

(i) In this case, without loss of generality, we may let $w_{j_1,i_1}=w_{j_1,1}$ and $w_{j_2,i_2}=w_{j_1,2}$. Since $f_{\varphi }\left(w_{j_1,1}\right)=f_{\varphi }\left(w_{r_1,s_1}\right)$ and $f_{\varphi }\left(w_{j_1,2}\right)=f_{\varphi }\left(w_{r_2,s_2}\right)$, it can be obtained from Claim 4 that $w_{r_1,s_1}$ and $w_{r_2,s_2}$ must be internal vertices of $V_{r_1}$ and $V_{r_2}$ respectively, furthermore both $r_1$ and $r_2$ are less than $j_1$. If $r_1\ne r_2$, then according to Claim 3 and the relations (7(7) ${\theta }_1=f_{\varphi }\left(w_{j,2}\right)-f_{\varphi }\left(w_{j,1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}\hfill \end{array}\right.$(7) ), (9(9) ${\theta }_3=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+2,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+2,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.$(9) ) and (10(10) $\begin{array}{cc}\hfill {\theta }_4=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=& f_{\varphi }\left(w_{j,n}\right)-f_{\varphi }\left(w_{j,n-1}\right)\hfill \\ \hfill =& \left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.\hfill \end{array}$(10) ) we can get that $\begin{array}{cc}\hfill |f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|& \ge max\{{\theta }_3,{\theta }_4\}=n^2+n+2\hfill \\ \hfill & >{\theta }_1=f_{\varphi }\left(w_{j_1,2}\right)-f_{\varphi }\left(w_{j_1,1}\right)=f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)\hfill \end{array}$which contradicts the relation (11(11) $f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)=f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right).$(11) ). Therefore it can be deduced that $r_1=r_2$, i.e., both $w_{r_1,s_1}$ and $w_{r_2,s_2}$ are internal vertices of $V_{r_1}$. Furthermore, combining (11(11) $f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)=f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right).$(11) ) we can get that $s_1\ne s_2$. Now, if $|s_1-s_2|>1$, then it can be deduced from Claim 3 and the relations (7(7) ${\theta }_1=f_{\varphi }\left(w_{j,2}\right)-f_{\varphi }\left(w_{j,1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}\hfill \end{array}\right.$(7) ), (9(9) ${\theta }_3=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+2,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+2,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.$(9) ) and (10(10) $\begin{array}{cc}\hfill {\theta }_4=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=& f_{\varphi }\left(w_{j,n}\right)-f_{\varphi }\left(w_{j,n-1}\right)\hfill \\ \hfill =& \left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.\hfill \end{array}$(10) ) that $\begin{array}{cc}\hfill |f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|& =|f_{\varphi }\left(w_{r_1,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|>max\{{\theta }_3,{\theta }_4\}=n^2+n+2\hfill \\ \hfill & >{\theta }_1=f_{\varphi }\left(w_{j_1,2}\right)-f_{\varphi }\left(w_{j_1,1}\right)=f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)\hfill \end{array}$which contradicts to the relation (11(11) $f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)=f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right).$(11) ). So it can be obtained that $|s_1-s_2|=1$, and therefore $|f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|=|f_{\varphi }\left(w_{r_1,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|\in \{{\theta }_3,{\theta }_4\}$. On the other hand, $f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)=f_{\varphi }\left(w_{j_1,2}\right)-f_{\varphi }\left(w_{j_1,1}\right)={\theta }_1$. So, combining (11(11) $f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)=f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right).$(11) ) it can be deduced that $w_{r_1,s_1}$ and $w_{r_2,s_2}$ must be the last two internal vertices $w_{r_1,n-1}$ and $w_{r_1,n}$ in $V_{r_1}$. And Claim 6 (i) is obtained.

(ii) In this case, let $h=max\{j_1,j_2\}$. Since $r_1=r_2$, the vertex $w_{r_2,s_2}$ is denoted by $w_{r_1,s_2}$. According to Claim 4 it can be deduced that both $w_{r_1,s_1}$ and $w_{r_1,s_2}$ are internal vertices of $V_{r_1}$, furthermore $r_1<min\{j_1,j_2\}$. Because $w_{j_1,i_1}$ and $w_{j_2,i_2}$ are endpoints of $V_{j_1}$ and $V_{j_2}$ respectively, according to (8(8) ${\theta }_2=f_{\varphi }\left(w_{j,1}\right)-f_{\varphi }\left(w_{j-1,2}\right)=\left\{\begin{array}{cccc}\hfill & 2n^3-n^2-2,\hfill & \hfill & 4\le j\le m-2\hfill \\ \hfill & 2n^3-\frac{1}{2}{n}^2-\frac{1}{2}n-2,\hfill & \hfill & j=m-1\hfill \\ \hfill & n^3-n^2+n-2\hfill & \hfill & j=m.\hfill \end{array}\right.$(8) ) and (11(11) $f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)=f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right).$(11) ) and Claim 2 we can get that (12) $\begin{array}{cc}\hfill & |f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|=|f_{\varphi }\left(w_{r_1,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|=|f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)|\hfill \\ \hfill & \ge f_{\varphi }\left(w_{h,1}\right)-f_{\varphi }\left(w_{h-1,2}\right)={\theta }_2=\left\{\begin{array}{cccc}\hfill & 2n^3-n^2-2,\hfill & \hfill & 4\le h\le m-2\hfill \\ \hfill & 2n^3-\frac{1}{2}{n}^2-\frac{1}{2}n-2,\hfill & \hfill & h=m-1\hfill \\ \hfill & n^3-n^2+n-2\hfill & \hfill & h=m.\hfill \end{array}\right.\hfill \end{array}$(12) On the other hand, since $r_1<min\{j_1,j_2\}<max\{j_1,j_2\}=h$, combining with (8(8) ${\theta }_2=f_{\varphi }\left(w_{j,1}\right)-f_{\varphi }\left(w_{j-1,2}\right)=\left\{\begin{array}{cccc}\hfill & 2n^3-n^2-2,\hfill & \hfill & 4\le j\le m-2\hfill \\ \hfill & 2n^3-\frac{1}{2}{n}^2-\frac{1}{2}n-2,\hfill & \hfill & j=m-1\hfill \\ \hfill & n^3-n^2+n-2\hfill & \hfill & j=m.\hfill \end{array}\right.$(8) )–(10(10) $\begin{array}{cc}\hfill {\theta }_4=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=& f_{\varphi }\left(w_{j,n}\right)-f_{\varphi }\left(w_{j,n-1}\right)\hfill \\ \hfill =& \left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.\hfill \end{array}$(10) ) it can be obtained that for $i\in \{4,5,\dots ,n\}$ $\begin{array}{cc}\hfill & |f_{\varphi }\left(w_{h,1}\right)-f_{\varphi }\left(w_{h-1,2}\right)|-2|f_{\varphi }\left(w_{r_1,i}\right)-f_{\varphi }\left(w_{r_1,i-1}\right)|\hfill \\ \hfill & \ge \left\{\begin{array}{cccc}\hfill & (2n^3-n^2-2)-2(n^2+n+2),\hfill & \hfill & 3\le r_1<h\le m-2\hfill \\ \hfill & (2n^3-\frac{n^2}{2}-\frac{n}{2}-2)-2(n^2+n+2),\hfill & \hfill & 3\le r_1\le m-2,h=m-1\hfill \\ \hfill & (n^3-n^2+n-2)-2(n^2+n+2),\hfill & \hfill & 3\le r_1\le m-1,h=m\hfill \end{array}\right.\hfill \\ \hfill & >0.\hfill \end{array}$From (12(12) $\begin{array}{cc}\hfill & |f_{\varphi }\left(w_{r_2,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|=|f_{\varphi }\left(w_{r_1,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|=|f_{\varphi }\left(w_{j_2,i_2}\right)-f_{\varphi }\left(w_{j_1,i_1}\right)|\hfill \\ \hfill & \ge f_{\varphi }\left(w_{h,1}\right)-f_{\varphi }\left(w_{h-1,2}\right)={\theta }_2=\left\{\begin{array}{cccc}\hfill & 2n^3-n^2-2,\hfill & \hfill & 4\le h\le m-2\hfill \\ \hfill & 2n^3-\frac{1}{2}{n}^2-\frac{1}{2}n-2,\hfill & \hfill & h=m-1\hfill \\ \hfill & n^3-n^2+n-2\hfill & \hfill & h=m.\hfill \end{array}\right.\hfill \end{array}$(12) ) we can get that $|f_{\varphi }\left(w_{r_1,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|\ge f_{\varphi }\left(w_{h,1}\right)-f_{\varphi }\left(w_{h-1,2}\right)$, and so $\begin{array}{cc}\hfill & |f_{\varphi }\left(w_{r_1,s_2}\right)-f_{\varphi }\left(w_{r_1,s_1}\right)|-2|f_{\varphi }\left(w_{r_1,i}\right)-f_{\varphi }\left(w_{r_1,i-1}\right)|\hfill \\ \hfill & \ge |f_{\varphi }\left(w_{h,1}\right)-f_{\varphi }\left(w_{h-1,2}\right)|-2|f_{\varphi }\left(w_{r_1,i}\right)-f_{\varphi }\left(w_{r_1,i-1}\right)|\hfill \\ \hfill & >0\hfill \end{array}$which indicates that $w_{r_1,s_1}$ and $w_{r_1,s_2}$ are separated by at least two other vertices of $V_{r_1}$, and Claim 6 (ii) is obtained.

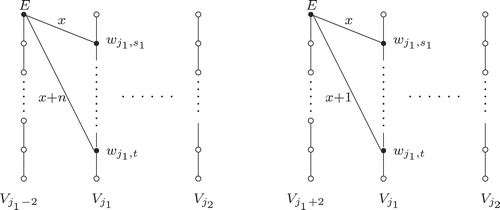
Under the labeling $\varphi$, if there are two vertices whose vertex-sums are equal, then the following two ways of modification can change them into unequal.

Modification on the labeling $\varphi$: Let $w_{j_1,s_1}$ be an internal vertex of $V_{j_1}$ and $w_{j_2,s_2}$ be an endpoint of $V_{j_2}$ with $j_1<j_2$. If $f_{\varphi }\left(w_{j_1,s_1}\right)=f_{\varphi }\left(w_{j_2,s_2}\right)$, then the following two ways of modification can make $f_{\varphi }\left(w_{j_1,s_1}\right)\ne f_{\varphi }\left(w_{j_2,s_2}\right)$ hold.

Modification-$A$: In this case, the labeling $\varphi$ is illustrated by the left of Fig. 3, where $w_{j_1,t}$ denotes the internal vertex which belongs to $\{w_{j_1,s_1-1},w_{j_1,s_1+1}\}$. The Modification-$A$ is choosing any vertex $E$ from $V_{j_1-2}$, and then exchanging the labels on edges $(E,w_{j_1,s_1})$ and $(E,w_{j_1,t})$. According to the expression (2(2) ${\mathbb{A}}_j=(m(n-1)+(j-1)n^2)\cdot {\mathbb{E}}_n+\mathbb{A},j=1,2,\dots ,m-2$(2) ) it can be obtained that, after the Modification $A$, $min\{f_{\varphi }\left(w_{j_1,s_1}\right),f_{\varphi }\left(w_{j_1,t}\right)\}$ increases by $n$, $max\{f_{\varphi }\left(w_{j_1,s_1}\right),f_{\varphi }\left(w_{j_1,t}\right)\}$ decreases by $n$, but the vertex-sums of all the other vertices remain unchanged.

Fig. 3 Modification $A$ and $B$.

Modification-$B$: In this case, the labeling $\varphi$ is illustrated by the right of Fig. 3, where $w_{j_1,t}$ denotes the internal vertex which belongs to $\{w_{j_1,s_1-1},w_{j_1,s_1+1}\}$. The Modification-$B$ is choosing any vertex $E$ from $V_{j_1+2}$, and then exchanging the labels on edges $(E,w_{j_1,s_1})$ and $(E,w_{j_1,t})$. According to the expression (2(2) ${\mathbb{A}}_j=(m(n-1)+(j-1)n^2)\cdot {\mathbb{E}}_n+\mathbb{A},j=1,2,\dots ,m-2$(2) ) it can be obtained that, after the Modification $B$, $min\{f_{\varphi }\left(w_{j_1,s_1}\right),f_{\varphi }\left(w_{j_1,t}\right)\}$ increases by $1$, $max\{f_{\varphi }\left(w_{j_1,s_1}\right),f_{\varphi }\left(w_{j_1,t}\right)\}$ decreases by $1$, but the vertex-sums of all the other vertices remain unchanged.

3 Proof of Theorem 1

Proof

The proof of Theorem 1 is discussed in the following three cases according to $m=2$, $m=3$, and $m\ge 4$ respectively.

Case 1. $m=2$.

Subcase 1.1 $n=2$

In this case, the graph is $P_2\left[P_2\right]$, and its antimagicness can be easily obtained.

Subcase 1.2 $n\ge 3$

In this case, the graph $P_2\left[P_n\right]$ is decomposed into $P_n^{\left(1\right)}$, $P_n^{\left(2\right)}$, and $K_{n,n}^{1,2}$. Firstly, we use $\{1,2,\dots ,n^2\}$ to label the complete bipartite graph $K_{n,n}^{1,2}$, and the labeling ${\varphi }_2:E\left(K_{n,n}^{1,2}\right)\to \{1,2,\dots ,n^2\}$ is represented by the generalized magic matrix. So we have $f_{{\varphi }_2}\left(w_{1,1}\right)=f_{{\varphi }_2}\left(w_{1,2}\right)=\cdots =f_{{\varphi }_2}\left(w_{1,n}\right)=f_{{\varphi }_2}\left(w_{2,1}\right)=f_{{\varphi }_2}\left(w_{2,2}\right)=\cdots =f_{{\varphi }_2}\left(w_{2,n}\right)=\frac{n}{2}(1+n^2).$Now, we use $\{n^2+1,n^2+2,\dots ,n^2+(2n-2)\}$ to label the edges of $P_n^{\left(1\right)}$ and $P_n^{\left(2\right)}$. For $j=1,2$, the graph labeling ${\varphi }_1$ on the edges of $P_n^{\left(j\right)}$ is defined as $\left\{\begin{array}{cc}\hfill & {\varphi }_1(w_{j,i},w_{j,i+2})=n^2+i+(j-1)(n-1),i\in \{1,2,\dots ,n-2\}\hfill \\ \hfill & {\varphi }_1(w_{j,n-1},w_{j,n})=n^2+(n-1)+(j-1)(n-1)\hfill \end{array}\right.$Through a calculation, the following monotonic sequences can be obtained $\left\{\begin{array}{cc}\hfill & f_{{\varphi }_1}\left(w_{1,1}\right)<f_{{\varphi }_1}\left(w_{1,2}\right)<f_{{\varphi }_1}\left(w_{2,1}\right)<f_{{\varphi }_1}\left(w_{2,2}\right)\hfill \\ \hfill & f_{{\varphi }_1}\left(w_{1,3}\right)<f_{{\varphi }_1}\left(w_{1,4}\right)<\cdots <f_{{\varphi }_1}\left(w_{1,n}\right)<f_{{\varphi }_1}\left(w_{2,3}\right)<f_{{\varphi }_1}\left(w_{2,4}\right)<\cdots <f_{{\varphi }_1}\left(w_{2,n}\right).\hfill \end{array}\right.$Since $\varphi ={\varphi }_1+{\varphi }_2$, from the above it can be obtained that (13) $\left\{\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)\hfill \\ \hfill & f_{\varphi }\left(w_{1,3}\right)<f_{\varphi }\left(w_{1,4}\right)<\cdots <f_{\varphi }\left(w_{1,n}\right)<f_{\varphi }\left(w_{2,3}\right)<f_{\varphi }\left(w_{2,4}\right)<\cdots <f_{\varphi }\left(w_{2,n}\right).\hfill \end{array}\right.$(13) Noticing that, for $n\ge 3$, we have (14) $\begin{array}{c}\hfill f_{\varphi }\left(w_{1,3}\right)-f_{\varphi }\left(w_{2,2}\right)=n^2-n+3>0.\end{array}$(14) From (13(10) $\begin{array}{cc}\hfill {\theta }_4=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=& f_{\varphi }\left(w_{j,n}\right)-f_{\varphi }\left(w_{j,n-1}\right)\hfill \\ \hfill =& \left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.\hfill \end{array}$(10) ) and (14(14) $\begin{array}{c}\hfill f_{\varphi }\left(w_{1,3}\right)-f_{\varphi }\left(w_{2,2}\right)=n^2-n+3>0.\end{array}$(14) ) we can get the following relation $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)\hfill \\ \hfill & <f_{\varphi }\left(w_{1,3}\right)<f_{\varphi }\left(w_{1,4}\right)<\cdots <f_{\varphi }\left(w_{1,n}\right)<f_{\varphi }\left(w_{2,3}\right)<f_{\varphi }\left(w_{2,4}\right)<\cdots <f_{\varphi }\left(w_{2,n}\right)\hfill \end{array}$and the antimagicness of $P_2\left[P_n\right]$ is obtained.

Case 2. $m=3$

Subcase 2.1 $n=2$

In this case, the graph is $P_3\left[P_2\right]$, and its antimagicness can be easily obtained.

Subcase 2.2 $n\ge 3$

In this case, the graph $P_3\left[P_n\right]$ is decomposed into $P_n^{\left(1\right)}$, $P_n^{\left(2\right)}$, $P_n^{\left(3\right)}$, $K_{n,n}^{1,3}$, and $K_{n,n}^{2,3}$. The labeling ${\varphi }_1$ is given by the expression (1(1) $\left\{\begin{array}{cc}\hfill & {\varphi }_1(w_{j,i},w_{j,i+2})=i+(j-1)(n-1),i\in \{1,2,\dots ,n-2\}\hfill \\ \hfill & {\varphi }_1(w_{j,n-1},w_{j,n})=(n-1)+(j-1)(n-1).\hfill \end{array}\right.$(1) ), ${\varphi }_2$ is given by the expressions (2(2) ${\mathbb{A}}_j=(m(n-1)+(j-1)n^2)\cdot {\mathbb{E}}_n+\mathbb{A},j=1,2,\dots ,m-2$(2) ) and (3(3) ${\mathbb{A}}_{m-1}=(m(n-1)+(m-2)n^2)\cdot {\mathbb{E}}_n+\mathbb{M},$(3) ), where $\left\{\begin{array}{cc}\hfill {\varphi }_1:& \{E\left(P_n^{\left(1\right)}\right)\cup E\left(P_n^{\left(2\right)}\right)\cup E\left(P_n^{\left(3\right)}\right)\}\to \{1,2,\dots ,3(n-1)\}\hfill \\ \hfill {\varphi }_2:& \{E\left(K_{n,n}^{1,3}\right)\cup E\left(K_{n,n}^{2,3}\right)\}\to \{3(n-1)+1,3(n-1)+2,\dots ,3(n-1)+2n^2\}.\hfill \end{array}\right.$According to Claim 1 it can be obtained that (15) $\left\{\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{1,3}\right)<\cdots <f_{\varphi }\left(w_{1,n}\right)\hfill \\ \hfill & f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)<f_{\varphi }\left(w_{2,3}\right)<\cdots <f_{\varphi }\left(w_{2,n}\right)\hfill \\ \hfill & f_{\varphi }\left(w_{3,1}\right)<f_{\varphi }\left(w_{3,2}\right)<f_{\varphi }\left(w_{3,3}\right)<\cdots <f_{\varphi }\left(w_{3n}\right)\hfill \end{array}\right..$(15) For $n\ge 3$, the following relations (16(15) $\left\{\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{1,3}\right)<\cdots <f_{\varphi }\left(w_{1,n}\right)\hfill \\ \hfill & f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)<f_{\varphi }\left(w_{2,3}\right)<\cdots <f_{\varphi }\left(w_{2,n}\right)\hfill \\ \hfill & f_{\varphi }\left(w_{3,1}\right)<f_{\varphi }\left(w_{3,2}\right)<f_{\varphi }\left(w_{3,3}\right)<\cdots <f_{\varphi }\left(w_{3n}\right)\hfill \end{array}\right..$(15) ) and (17$\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{1,3}\right)<\cdots <f_{\varphi }\left(w_{1,n}\right)\hfill \\ \hfill & <f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)<f_{\varphi }\left(w_{2,3}\right)<\cdots <f_{\varphi }\left(w_{2,n}\right)\hfill \\ \hfill & <f_{\varphi }\left(w_{3,1}\right)<f_{\varphi }\left(w_{3,2}\right)<f_{\varphi }\left(w_{3,3}\right)<\cdots <f_{\varphi }\left(w_{3n}\right)\hfill \end{array}$) can be obtained through some calculations (16) $\begin{array}{c}\hfill f_{\varphi }\left(w_{2,1}\right)-f_{\varphi }\left(w_{1,n}\right)=n^3-\frac{1}{2}{n}^2-\frac{1}{2}n+3>0\end{array}$(16) (17) $\begin{array}{c}\hfill f_{\varphi }\left(w_{3,1}\right)-f_{\varphi }\left(w_{2,n}\right)=\frac{7}{2}{n}^2-\frac{9}{2}n+4>0.\end{array}$(17) From (15(15) $\left\{\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{1,3}\right)<\cdots <f_{\varphi }\left(w_{1,n}\right)\hfill \\ \hfill & f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)<f_{\varphi }\left(w_{2,3}\right)<\cdots <f_{\varphi }\left(w_{2,n}\right)\hfill \\ \hfill & f_{\varphi }\left(w_{3,1}\right)<f_{\varphi }\left(w_{3,2}\right)<f_{\varphi }\left(w_{3,3}\right)<\cdots <f_{\varphi }\left(w_{3n}\right)\hfill \end{array}\right..$(15) )–(17(17) $\begin{array}{c}\hfill f_{\varphi }\left(w_{3,1}\right)-f_{\varphi }\left(w_{2,n}\right)=\frac{7}{2}{n}^2-\frac{9}{2}n+4>0.\end{array}$(17) ) we can get the following relation $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{1,3}\right)<\cdots <f_{\varphi }\left(w_{1,n}\right)\hfill \\ \hfill & <f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)<f_{\varphi }\left(w_{2,3}\right)<\cdots <f_{\varphi }\left(w_{2,n}\right)\hfill \\ \hfill & <f_{\varphi }\left(w_{3,1}\right)<f_{\varphi }\left(w_{3,2}\right)<f_{\varphi }\left(w_{3,3}\right)<\cdots <f_{\varphi }\left(w_{3n}\right)\hfill \end{array}$and the antimagicness of $P_3\left[P_n\right]$ is obtained.

Case 3. $m\ge 4$

Subcase 3.1 $n=2$

In this case, the graph is $P_m\left[P_2\right]$. The antimagicness of $P_m\left[P_2\right]$ can be easily obtained from the labeling illustrated by Fig. 4.

Subcase 3.2 $n=3$

In this case, the graph $P_m\left[P_3\right]$ is decomposed into $P_3^{\left(1\right)}$, $P_3^{\left(3\right)}$, …, $P_3^{\left(m\right)}$, $\dots$, $P_3^{\left(4\right)}$, $P_3^{\left(2\right)}$, and $K_{3,3}^{1,3}$, $K_{3,3}^{3,5}$, $\dots$, $K_{3,3}^{m-1,m}$, $\dots$, $K_{3,3}^{4,6}$, $K_{3,3}^{2,4}$. The labeling ${\varphi }_1$ is given by the expression (1(1) $\left\{\begin{array}{cc}\hfill & {\varphi }_1(w_{j,i},w_{j,i+2})=i+(j-1)(n-1),i\in \{1,2,\dots ,n-2\}\hfill \\ \hfill & {\varphi }_1(w_{j,n-1},w_{j,n})=(n-1)+(j-1)(n-1).\hfill \end{array}\right.$(1) ), ${\varphi }_2$ is given by the expressions (2(2) ${\mathbb{A}}_j=(m(n-1)+(j-1)n^2)\cdot {\mathbb{E}}_n+\mathbb{A},j=1,2,\dots ,m-2$(2) ) and (3(3) ${\mathbb{A}}_{m-1}=(m(n-1)+(m-2)n^2)\cdot {\mathbb{E}}_n+\mathbb{M},$(3) ), where $\left\{\begin{array}{cc}\hfill {\varphi }_1:& \{E\left(P_3^{\left(1\right)}\right)\cup E\left(P_3^{\left(2\right)}\right)\cup \cdots \cup E\left(P_3^{\left(m\right)}\right)\}\to \{1,2,\dots ,2m\}\hfill \\ \hfill {\varphi }_2:& \{E\left(K_{3,3}^{1,3}\right)\cup E\left(K_{3,3}^{3,5}\right)\cup \cdots \cup E\left(K_{3,3}^{m-1,m}\right)\cup \cdots \cup E\left(K_{3,3}^{4,6}\right)\cup E\left(K_{3,3}^{2,4}\right)\}\hfill \\ \hfill & \to \{2m+1,2m+2,\dots ,2m+9(m-1)\}\hfill \end{array}\right.$According to Claim 2 it can be obtained that the vertex-sums of all endpoints in this case satisfy the relation (5(5) $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)<\cdots <f_{\varphi }\left(w_{j,1}\right)<f_{\varphi }\left(w_{j,2}\right)\hfill \\ \hfill & <\cdots <f_{\varphi }\left(w_{m-1,1}\right)<f_{\varphi }\left(w_{m-1,2}\right)<f_{\varphi }\left(w_{m,1}\right)<f_{\varphi }\left(w_{m,2}\right).\hfill \end{array}$(5) ). Furthermore, through some calculations we can get that the vertex-sums of all internal vertices in this case satisfy (18) $f_{\varphi }\left(w_{1,3}\right)<f_{\varphi }\left(w_{2,3}\right)<\cdots <f_{\varphi }\left(w_{m,3}\right).$(18) So, if there is no endpoint whose vertex-sum equals one of the internal vertex’s vertex-sum, then the antimagicness of $P_m\left[P_3\right]$ is obtained. If there exists an endpoint whose vertex-sum is equal to that of an internal vertex, say, $f_{\varphi }\left(w_{j,1}\right)=f_{\varphi }\left(w_{k,3}\right)$ with $3\le k<j$ according to Claim 4, then the antimagicness of $P_m\left[P_3\right]$ can be obtained from one of the following two methods.

Method- 1: Exchanging the labeling on the edges $(w_{j-2,3},w_{j,1})$ and $(w_{j-2,3},w_{j,2})$.

After the exchanging, the vertex-sums of $w_{j,1}$ and $w_{j,2}$ have been changed and denoted by $\overline{f_{\varphi }\left(w_{j,1}\right)}$ and $\overline{f_{\varphi }\left(w_{j,2}\right)}$ respectively, but the vertex-sums of all the other vertices remain unchanged. It can be obtained that $\left\{\begin{array}{c}\hfill \overline{f_{\varphi }\left(w_{j,1}\right)}=f_{\varphi }\left(w_{j,1}\right)+n=f_{\varphi }\left(w_{j,1}\right)+3\\ \hfill \overline{f_{\varphi }\left(w_{j,2}\right)}=f_{\varphi }\left(w_{j,2}\right)-n=f_{\varphi }\left(w_{j,2}\right)-3.\end{array}\right.$Furthermore, from the relations (5(5) $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)<\cdots <f_{\varphi }\left(w_{j,1}\right)<f_{\varphi }\left(w_{j,2}\right)\hfill \\ \hfill & <\cdots <f_{\varphi }\left(w_{m-1,1}\right)<f_{\varphi }\left(w_{m-1,2}\right)<f_{\varphi }\left(w_{m,1}\right)<f_{\varphi }\left(w_{m,2}\right).\hfill \end{array}$(5) ) and (18$\left\{\begin{array}{cc}\hfill {\varphi }_1:& \{E\left(P_3^{\left(1\right)}\right)\cup E\left(P_3^{\left(2\right)}\right)\cup \cdots \cup E\left(P_3^{\left(m\right)}\right)\}\to \{1,2,\dots ,2m\}\hfill \\ \hfill {\varphi }_2:& \{E\left(K_{3,3}^{1,3}\right)\cup E\left(K_{3,3}^{3,5}\right)\cup \cdots \cup E\left(K_{3,3}^{m-1,m}\right)\cup \cdots \cup E\left(K_{3,3}^{4,6}\right)\cup E\left(K_{3,3}^{2,4}\right)\}\hfill \\ \hfill & \to \{2m+1,2m+2,\dots ,2m+9(m-1)\}\hfill \end{array}\right.$) and some calculations we can get that $\left\{\begin{array}{cc}\hfill & \cdots <f_{\varphi }\left(w_{j-1,2}\right)<f_{\varphi }\left(w_{j,1}\right)<\overline{f_{\varphi }\left(w_{j,1}\right)}<\overline{f_{\varphi }\left(w_{j,2}\right)}<f_{\varphi }\left(w_{j,2}\right)<f_{\varphi }\left(w_{j+1,1}\right)<\cdots \hfill \\ \hfill & \cdots <f_{\varphi }\left(w_{k-1,3}\right)<f_{\varphi }\left(w_{k,3}\right)=f_{\varphi }\left(w_{j,1}\right)<\overline{f_{\varphi }\left(w_{j,1}\right)}<\overline{f_{\varphi }\left(w_{j,2}\right)}<f_{\varphi }\left(w_{k+1,3}\right)<\cdots \hfill \end{array}\right.$

Method- 2: Exchanging the labeling on the edges $(w_{j+2,3},w_{j,1})$ and $(w_{j+2,3},w_{j,2})$

Similar to that of the method-1, we can get that $\overline{f_{\varphi }\left(w_{j,1}\right)}$ and $\overline{f_{\varphi }\left(w_{j,2}\right)}$ in this case satisfy the following relations. $\left\{\begin{array}{c}\hfill \overline{f_{\varphi }\left(w_{j,1}\right)}=f_{\varphi }\left(w_{j,1}\right)+1\\ \hfill \overline{f_{\varphi }\left(w_{j,2}\right)}=f_{\varphi }\left(w_{j,2}\right)-1.\end{array}\right.$Furthermore, from the relations (5(5) $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)<\cdots <f_{\varphi }\left(w_{j,1}\right)<f_{\varphi }\left(w_{j,2}\right)\hfill \\ \hfill & <\cdots <f_{\varphi }\left(w_{m-1,1}\right)<f_{\varphi }\left(w_{m-1,2}\right)<f_{\varphi }\left(w_{m,1}\right)<f_{\varphi }\left(w_{m,2}\right).\hfill \end{array}$(5) ) and (18$\left\{\begin{array}{cc}\hfill {\varphi }_1:& \{E\left(P_3^{\left(1\right)}\right)\cup E\left(P_3^{\left(2\right)}\right)\cup \cdots \cup E\left(P_3^{\left(m\right)}\right)\}\to \{1,2,\dots ,2m\}\hfill \\ \hfill {\varphi }_2:& \{E\left(K_{3,3}^{1,3}\right)\cup E\left(K_{3,3}^{3,5}\right)\cup \cdots \cup E\left(K_{3,3}^{m-1,m}\right)\cup \cdots \cup E\left(K_{3,3}^{4,6}\right)\cup E\left(K_{3,3}^{2,4}\right)\}\hfill \\ \hfill & \to \{2m+1,2m+2,\dots ,2m+9(m-1)\}\hfill \end{array}\right.$) and some calculations we can get that $\left\{\begin{array}{cc}\hfill & \cdots <f_{\varphi }\left(w_{j-1,2}\right)<f_{\varphi }\left(w_{j,1}\right)<\overline{f_{\varphi }\left(w_{j,1}\right)}<\overline{f_{\varphi }\left(w_{j,2}\right)}<f_{\varphi }\left(w_{j,2}\right)<f_{\varphi }\left(w_{j+1,1}\right)<\cdots \hfill \\ \hfill & \cdots <f_{\varphi }\left(w_{k-1,3}\right)<f_{\varphi }\left(w_{k,3}\right)=f_{\varphi }\left(w_{j,1}\right)<\overline{f_{\varphi }\left(w_{j,1}\right)}<\overline{f_{\varphi }\left(w_{j,2}\right)}<f_{\varphi }\left(w_{k+1,3}\right)<\cdots \hfill \end{array}\right.$

Keep Claims 4 and 6 (i) in mind, and repeat the above process if there are still other pairs of vertex-sum being equal. From the above discussion we can get the antimagicness of $P_m\left[P_3\right]$.

Subcase 3.3 $n\ge 4$

In this case, the graph $P_m\left[P_n\right]$ is decomposed into $m$ copies of the path $P_n^{\left(1\right)}$, $P_n^{\left(3\right)}$, $\dots$, $P_n^{\left(m\right)}$, $\dots$, $P_n^{\left(4\right)}$, $P_n^{\left(2\right)}$, and $m-1$ copies of the complete bipartite graphs $K_{n,n}^{1,3}$, $K_{n,n}^{3,5}$, $\dots$, $K_{n,n}^{m-1,m}$, $\dots$, $K_{n,n}^{4,6}$, $K_{n,n}^{2,4}$. The labeling ${\varphi }_1$ is given by the expression (1(1) $\left\{\begin{array}{cc}\hfill & {\varphi }_1(w_{j,i},w_{j,i+2})=i+(j-1)(n-1),i\in \{1,2,\dots ,n-2\}\hfill \\ \hfill & {\varphi }_1(w_{j,n-1},w_{j,n})=(n-1)+(j-1)(n-1).\hfill \end{array}\right.$(1) ), ${\varphi }_2$ is given by the expressions (2(2) ${\mathbb{A}}_j=(m(n-1)+(j-1)n^2)\cdot {\mathbb{E}}_n+\mathbb{A},j=1,2,\dots ,m-2$(2) ) and (3(3) ${\mathbb{A}}_{m-1}=(m(n-1)+(m-2)n^2)\cdot {\mathbb{E}}_n+\mathbb{M},$(3) ), where $\left\{\begin{array}{cc}\hfill {\varphi }_1:& \{E\left(P_n^{\left(1\right)}\right)\cup E\left(P_n^{\left(2\right)}\right)\cup \cdots \cup E\left(P_n^{\left(m\right)}\right)\}\to \{1,2,\dots ,m(n-1)\}\hfill \\ \hfill {\varphi }_2:& \{E\left(K_{n,n}^{1,3}\right)\cup E\left(K_{n,n}^{3,5}\right)\cup \cdots \cup E\left(K_{n,n}^{m-1,m}\right)\cup \cdots \cup E\left(K_{n,n}^{4,6}\right)\cup E\left(K_{n,n}^{2,4}\right)\}\hfill \\ \hfill & \to \{m(n-1)+1,m(n-1)+2,\dots ,m(n-1)+(m-1)n^2\}.\hfill \end{array}\right.$For convenience, the endpoint’s vertex-sums $f_{\varphi }\left(w_{1,1}\right)$, $f_{\varphi }\left(w_{1,2}\right)$, $f_{\varphi }\left(w_{2,1}\right)$, $f_{\varphi }\left(w_{2,2}\right)$, $\dots$, $f_{\varphi }\left(w_{m,1}\right)$, and $f_{\varphi }\left(w_{m,2}\right)$ are represented by $x_1$, $x_2$, $x_3$, $\dots$, $x_{2m-1}$ and $x_{2m}$ respectively. The internal vertex’s vertex-sums $f_{\varphi }\left(w_{1,3}\right)$, $f_{\varphi }\left(w_{1,4}\right)$, $\dots$, $f_{\varphi }\left(w_{1,n}\right)$, $f_{\varphi }\left(w_{2,3}\right)$, $f_{\varphi }\left(w_{2,4}\right)$, $\dots$, $f_{\varphi }\left(w_{2,n}\right)$, $\dots$, $f_{\varphi }\left(w_{m,3}\right)$, $f_{\varphi }\left(w_{m,4}\right)$, $\dots$, $f_{\varphi }\left(w_{m,n}\right)$ are represented by $y_1$, $y_2$, $y_3$, $\dots$, $y_{m(n-2)}$ respectively. Let $X_0=\{x_1,x_2,\dots ,x_{2m}\}$, $Y_0=\{y_1,y_2,\dots ,y_{m(n-2)}\}$. According to Claims 2 and 3, it can be obtained that the elements in $X_0$ and $Y_0$ satisfy the following two monotonic sequences.

$X_0:x_1<x_2<x_3<\cdots <x_{2m-1}<x_{2m}$$Y_0:y_1<y_2<y_3<\cdots <y_{m(n-2)}.$

If the elements in $X_0$ and $Y_0$ are pairwise distinct, then the antimagicness of $P_m\left[P_n\right]$ in this case can be obtained. If there exist some elements in $X_0$ which are equal to some elements in $Y_0$ respectively, then these elements in $X_0$ and $Y_0$ are denoted by $X_1=\{x_{i_1},x_{i_2},\dots ,x_{i_s}\}$ and $Y_1=\{y_{j_1},y_{j_2},\dots ,y_{j_s}\}$ respectively, where $x_{i_k}=y_{j_k}$ for $1\le k\le s$. According to Claims 2 and 3 we may let the elements in $X_1$ and $Y_1$ satisfy the following two monotonic sequences.

$X_1:x_{i_1}<x_{i_2}<x_{i_3}<\cdots <x_{i_s}$$Y_1:y_{j_1}<y_{j_2}<y_{j_3}<\cdots <y_{j_s}.$

After the operations of the following two steps, the elements in $X_0$ and $Y_0$ will be pairwise distinct.

Step 1.

In $X_1$, if there exist two elements $x_{i_{k_1}}$ and $x_{i_{k_2}}$ $(i_{k_1}<i_{k_2})$ being the vertex-sums of the two endpoints in the same $V_{\alpha }$, where $4\le \alpha \le m$ according to Claim 4, then from Claim 6 (i) we can get that $y_{j_{k_1}}$ and $y_{j_{k_2}}$ must be the last two internal vertices of $V_{\beta }$ with $\beta <\alpha$, i.e., $f_{\varphi }\left(w_{\alpha ,1}\right)=x_{i_{k_1}}=y_{j_{k_1}}=f_{\varphi }\left(w_{\beta ,n-1}\right)<f_{\varphi }\left(w_{\alpha ,2}\right)=x_{i_{k_2}}=y_{j_{k_2}}=f_{\varphi }\left(w_{\beta ,n}\right).$Now, make the Modification $A$ on $\varphi$, i.e., choose any vertex $E$ from $V_{\beta -2}$ and then exchange the labels on edges $(E,w_{\beta ,n-1})$ and $(E,w_{\beta ,n})$. After the Modification $A$, $y_{j_{k_1}}$ and $y_{j_{k_2}}$ are replaced by $y_{j_{k_1}}^{\prime }$ and $y_{j_{k_2}}^{\prime }$ respectively, where $y_{j_{k_1}}^{\prime }=y_{j_{k_1}}+n$, $y_{j_{k_2}}^{\prime }=y_{j_{k_2}}-n$, but the vertex-sums of all the other vertices remain unchanged. According to the relation (10(10) $\begin{array}{cc}\hfill {\theta }_4=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=& f_{\varphi }\left(w_{j,n}\right)-f_{\varphi }\left(w_{j,n-1}\right)\hfill \\ \hfill =& \left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.\hfill \end{array}$(10) ) it can be obtained that the footstep between $y_{j_{k_1}}^{\prime }$ and $y_{j_{k_2}}^{\prime }$ is $\begin{array}{cc}\hfill y_{j_{k_2}}^{\prime }-y_{j_{k_1}}^{\prime }& =(y_{j_{k_2}}-n)-(y_{j_{k_1}}+n)=(y_{j_{k_2}}-y_{j_{k_1}})-2n\hfill \\ \hfill & =\left\{\begin{array}{cccc}\hfill & n^2-n+1,\hfill & \hfill & 3\le \beta <\alpha \le m-1\hfill \\ \hfill & n^2-2n+1,\hfill & \hfill & \beta =m-1,\alpha =m\hfill \end{array}\right.\hfill \\ \hfill & >0.\hfill \end{array}$Therefore $y_{j_{k_2}}^{\prime }>y_{j_{k_1}}^{\prime }$, and the following relation can be obtained (19) $x_{i_{k_1}}=y_{j_{k_1}}<y_{j_{k_1}}^{\prime }<y_{j_{k_2}}^{\prime }<y_{j_{k_2}}=x_{i_{k_2}}.$(19) Noticing that $x_{i_{k_1}}$ and $x_{i_{k_2}}$ are the vertex-sums of the two endpoints in $V_{\alpha }$, $y_{j_{k_1}}$ and $y_{j_{k_2}}$ are the vertex-sums of the last two internal vertices in $V_{\beta }$, combining (5(5) $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,1}\right)<f_{\varphi }\left(w_{1,2}\right)<f_{\varphi }\left(w_{2,1}\right)<f_{\varphi }\left(w_{2,2}\right)<\cdots <f_{\varphi }\left(w_{j,1}\right)<f_{\varphi }\left(w_{j,2}\right)\hfill \\ \hfill & <\cdots <f_{\varphi }\left(w_{m-1,1}\right)<f_{\varphi }\left(w_{m-1,2}\right)<f_{\varphi }\left(w_{m,1}\right)<f_{\varphi }\left(w_{m,2}\right).\hfill \end{array}$(5) ), (6(6) $\begin{array}{cc}\hfill & f_{\varphi }\left(w_{1,3}\right)<f_{\varphi }\left(w_{1,4}\right)<\cdots <f_{\varphi }\left(w_{1,n}\right)\hfill \\ \hfill & <f_{\varphi }\left(w_{2,3}\right)<f_{\varphi }\left(w_{2,4}\right)<\cdots <f_{\varphi }\left(w_{2,n}\right)<\hfill \\ \hfill & \cdots \cdots \cdots \cdots \hfill \\ \hfill & <f_{\varphi }\left(w_{m-1,3}\right)<f_{\varphi }\left(w_{m-1,4}\right)<\cdots <f_{\varphi }\left(w_{m-1,n}\right)\hfill \\ \hfill & <f_{\varphi }\left(w_{m,3}\right)<f_{\varphi }\left(w_{m,4}\right)<\cdots <f_{\varphi }\left(w_{m,n}\right).\hfill \end{array}$(6) ) and (19(19) $x_{i_{k_1}}=y_{j_{k_1}}<y_{j_{k_1}}^{\prime }<y_{j_{k_2}}^{\prime }<y_{j_{k_2}}=x_{i_{k_2}}.$(19) ) it can be deduced that there is no element in $X_0$ and $Y_0$ being equal to $y_{j_{k_1}}^{\prime }$ or $y_{j_{k_2}}^{\prime }$.

If there are still other pair of elements in $X_1$, say, $x_{i_{k_3}}$ and $x_{i_{k_4}}$, being the vertex-sums of the two endpoints in the same $V_{\gamma }$ ($4\le \gamma \le m$ according to Claim 4), then repeat the above modification process, and so on.

Step 2.

After the Step 1, if the elements in $X_1$ and $Y_1$ are pairwise distinct, then the antimagicness of $P_m\left[P_n\right]$ can be obtained. If there still exist some elements in $X_1$ which are equal to some elements in $Y_1$ respectively, then these elements in $X_1$ and $Y_1$ are denoted by $X_2=\{x_{p_1},x_{p_2},\dots ,x_{p_t}\}$ and $Y_2=\{y_{q_1},y_{q_2},\dots ,y_{q_t}\}$ respectively, where $x_{p_i}=y_{q_i}$ for $1\le i\le t$. Without loss of generality, let the elements in $X_2$ and $Y_2$ satisfy the following two monotonic sequences.

$X_2:x_{p_1}<x_{p_2}<x_{p_3}<\cdots <x_{p_t}$$Y_2:y_{q_1}<y_{q_2}<y_{q_3}<\cdots <y_{q_t}.$

For the convenience of expression, let $x_{p_i}=f_{\varphi }\left(v_i\right)$ and $y_{q_i}=f_{\varphi }\left({\tilde{v}}_i\right)$, where $v_i$ and ${\tilde{v}}_i$ is an endpoint and an internal vertex of $P_m\left[P_n\right]$ respectively ($1\le i\le t$). Let ${\Omega }_1=\{v_1,v_2,\dots ,v_t\}$, ${\Omega }_2=\{{\tilde{v}}_1,{\tilde{v}}_2,\dots ,{\tilde{v}}_t\}$. We can get that, after the Step 1, any two elements in ${\Omega }_1$ cannot be the two endpoints which are in the same $V_{\alpha }(4\le \alpha \le m)$. And therefore, according to Claim 6 we can get that any two elements in ${\Omega }_2$ either are internal vertices which are in different $V_{\beta }$ and $V_{\gamma }$ ($\beta \ne \gamma$) respectively, or are the internal vertices which are both in $V_{\beta }$ but they are separated by at least two other internal vertices of $V_{\beta }$, where $3\le \beta ,\gamma \le m-1$ according to Claim 4.

Let $v_i$ and ${\tilde{v}}_i$ be the elements selected arbitrarily from ${\Omega }_1$ and ${\Omega }_2$ respectively. Without loss of generality, we may let $v_i=w_{\alpha ,c}$, ${\tilde{v}}_i=w_{\beta ,d}$, i.e., $f_{\varphi }\left(w_{\alpha ,c}\right)=f_{\varphi }\left(v_i\right)=x_{p_i}=y_{q_i}=f_{\varphi }\left({\tilde{v}}_i\right)=f_{\varphi }\left(w_{\beta ,d}\right),$where $3\le \beta <\alpha \le m$, $c\in \{1,2\}$, $d\in \{3,4,\dots ,n\}$.

(i) If $\alpha =m$ and $\beta =m-1$, i.e., $v_i(=w_{\alpha ,c})$ is one of the endpoints in $V_m$ and ${\tilde{v}}_i(=w_{\beta ,d})$ is one of the internal vertices in $V_{m-1}$, then make the Modification $A$ on $\varphi$, that is to say, choose any vertex $E$ from $V_{\beta -2}$ and then exchange the labels on edges $(E,w_{\beta ,d})$ and $(E,w_{\beta ,e})$, where $e$ is one of $\{d-1,d+1\}$ which belongs to $\{3,4,\dots ,n\}$.

(ii) If $\alpha \in \{m-1,m\}$ and $\beta \in \{3,4,\dots ,m-2\}$, then make the Modification $B$ on $\varphi$, that is to say, choose any vertex $E$ from $V_{\beta +2}$ and then exchange the labels on edges $(E,w_{\beta ,d})$ and $(E,w_{\beta ,e})$, where $e$ is one of $\{d-1,d+1\}$ which belongs to $\{3,4,\dots ,n\}$.

(iii) If $3\le \beta <\alpha \le m-2$, then make the Modification $A$ on $\varphi$, that is to say, choose any vertex $E$ from $V_{\beta -2}$ and then exchange the labels on edges $(E,w_{\beta ,d})$ and $(E,w_{\beta ,e})$, where $e$ is one of $\{d-1,d+1\}$ which belongs to $\{3,4,\dots ,n\}$.

Make the above modification on all elements in ${\Omega }_2$. After the Modification $A$ (or $B$), $min\left\{f_{\varphi }\left(w_{\beta ,d}\right)f_{\varphi }\left(w_{\beta ,e}\right)\right\}$, increases by $n$ (or 1), and $max\left\{f_{\varphi }\left(w_{\beta ,d}\right)f_{\varphi }\left(w_{\beta ,e}\right)\right\}$, decreases by $n$ (or 1), but the vertex-sums of all the other vertices remain unchanged. Let $\overline{f_{\varphi }\left(w_{\beta ,d}\right)}$ and $\overline{f_{\varphi }\left(w_{\beta ,e}\right)}$ denote, after the Modification A (or B), the vertex-sums of $w_{\beta ,d}$ and $w_{\beta ,e}$ respectively. In the following we will show that, after the modification, no elements in $X_0$ and $Y_0$ can be equal to $\overline{f_{\varphi }\left(w_{\beta ,d}\right)}$ or $\overline{f_{\varphi }\left(w_{\beta ,e}\right)}$, and therefore the antimagicness of $P_m\left[P_n\right]$ can be deduced.

The proof methods for (i), (ii) and (iii) are similar, and here we only give the proof for (iii). Without loss of generality, we may let $w_{\beta ,e}=w_{\beta ,d-1}$ and the modification be of type $A$. After the Modification $A$, the vertex-sum $f_{\varphi }\left(w_{\beta ,d-1}\right)$ of $w_{\beta ,d-1}$ increases by $n$ and changed into $\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}$, the vertex-sum $f_{\varphi }\left(w_{\beta ,d}\right)$ of $w_{\beta ,d}$ decreases by $n$ and changed into $\overline{f_{\varphi }\left(w_{\beta ,d}\right)}$. For convenience of expression, the elements in $X_0$ and $Y_0$ are represented by the following. (20) $\begin{array}{cc}\hfill & X_0:f_{\varphi }\left(w_{1,1}\right)<\cdots <f_{\varphi }\left(w_{\xi ,c_1}\right)<f_{\varphi }\left(w_{\alpha ,c}\right)<\cdots <f_{\varphi }\left(w_{m,2}\right)\hfill \\ \hfill & Y_0:f_{\varphi }\left(w_{1,3}\right)<\cdots <f_{\varphi }\left(w_{\beta ,d-1}\right)<f_{\varphi }\left(w_{\beta ,d}\right)<\cdots <f_{\varphi }\left(w_{m,n}\right).\hfill \end{array}$(20) Since $3\le \beta <\alpha \le m-2$, according to the relations (7(7) ${\theta }_1=f_{\varphi }\left(w_{j,2}\right)-f_{\varphi }\left(w_{j,1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}\hfill \end{array}\right.$(7) ,8(8) ${\theta }_2=f_{\varphi }\left(w_{j,1}\right)-f_{\varphi }\left(w_{j-1,2}\right)=\left\{\begin{array}{cccc}\hfill & 2n^3-n^2-2,\hfill & \hfill & 4\le j\le m-2\hfill \\ \hfill & 2n^3-\frac{1}{2}{n}^2-\frac{1}{2}n-2,\hfill & \hfill & j=m-1\hfill \\ \hfill & n^3-n^2+n-2\hfill & \hfill & j=m.\hfill \end{array}\right.$(8) ) we can get that the footstep between the two endpoints $w_{\alpha ,c}$ and $w_{\xi ,c_1}$ is (21) $f_{\varphi }\left(w_{\alpha ,c}\right)-f_{\varphi }\left(w_{\xi ,c_1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & \xi =\alpha ,c=2,c_1=1\hfill \\ \hfill & 2n^3-n^2-2,\hfill & \hfill & \xi =\alpha -1,c=1,c_1=2.\hfill \end{array}\right.$(21) And according to the relations (9(9) ${\theta }_3=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+2,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+2,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.$(9) ) and (10(10) $\begin{array}{cc}\hfill {\theta }_4=f_{\varphi }\left(w_{j,i}\right)-f_{\varphi }\left(w_{j,i-1}\right)=& f_{\varphi }\left(w_{j,n}\right)-f_{\varphi }\left(w_{j,n-1}\right)\hfill \\ \hfill =& \left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & 3\le j\le m-2\hfill \\ \hfill & n^2+1,\hfill & \hfill & j\in \{m-1,m\}.\hfill \end{array}\right.\hfill \end{array}$(10) ) we can get that (22) $f_{\varphi }\left(w_{\beta ,d}\right)-f_{\varphi }\left(w_{\beta ,d-1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+2,\hfill & \hfill & 4\le d\le n-1\hfill \\ \hfill & n^2+n+1,\hfill & \hfill & d=n.\hfill \end{array}\right.$(22) From the relation (22(22) $f_{\varphi }\left(w_{\beta ,d}\right)-f_{\varphi }\left(w_{\beta ,d-1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+2,\hfill & \hfill & 4\le d\le n-1\hfill \\ \hfill & n^2+n+1,\hfill & \hfill & d=n.\hfill \end{array}\right.$(22) ) it can be obtained that $\begin{array}{cc}\hfill \overline{f_{\varphi }\left(w_{\beta ,d}\right)}-\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}& =(f_{\varphi }\left(w_{\beta ,d}\right)-n)-(f_{\varphi }\left(w_{\beta ,d-1}\right)+n)\hfill \\ \hfill & =(f_{\varphi }\left(w_{\beta ,d}\right)-f_{\varphi }\left(w_{\beta ,d-1}\right))-2n\hfill \\ \hfill & =\left\{\begin{array}{cccc}\hfill & n^2-n+2,\hfill & \hfill & 4\le d\le n-1\hfill \\ \hfill & n^2-n+1,\hfill & \hfill & d=n\hfill \end{array}\right.\hfill \\ \hfill & >0.\hfill \end{array}$So, the following inequality can be obtained (23) $\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}<\overline{f_{\varphi }\left(w_{\beta ,d}\right)}.$(23) Since $f_{\varphi }\left(w_{\alpha ,c}\right)=f_{\varphi }\left(w_{\beta ,d}\right)$, combining with (21(21) $f_{\varphi }\left(w_{\alpha ,c}\right)-f_{\varphi }\left(w_{\xi ,c_1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+1,\hfill & \hfill & \xi =\alpha ,c=2,c_1=1\hfill \\ \hfill & 2n^3-n^2-2,\hfill & \hfill & \xi =\alpha -1,c=1,c_1=2.\hfill \end{array}\right.$(21) ) and (22(22) $f_{\varphi }\left(w_{\beta ,d}\right)-f_{\varphi }\left(w_{\beta ,d-1}\right)=\left\{\begin{array}{cccc}\hfill & n^2+n+2,\hfill & \hfill & 4\le d\le n-1\hfill \\ \hfill & n^2+n+1,\hfill & \hfill & d=n.\hfill \end{array}\right.$(22) ) it can be obtained that $\begin{array}{cc}\hfill f_{\varphi }\left(w_{\alpha ,c}\right)-\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}& =f_{\varphi }\left(w_{\beta ,d}\right)-(f_{\varphi }\left(w_{\beta ,d-1}\right)+n)\hfill \\ \hfill & =(f_{\varphi }\left(w_{\beta ,d}\right)-f_{\varphi }\left(w_{\beta ,d-1}\right))-n\hfill \\ \hfill & =\left\{\begin{array}{cccc}\hfill & n^2+2,\hfill & \hfill & 4\le d\le n-1\hfill \\ \hfill & n^2+1,\hfill & \hfill & d=n\hfill \end{array}\right.\hfill \\ \hfill & <f_{\varphi }\left(w_{\alpha ,c}\right)-f_{\varphi }\left(w_{\xi ,c_1}\right).\hfill \end{array}$So, $f_{\varphi }\left(w_{\xi ,c_1}\right)<\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}$. Combining this inequality with (20(20) $\begin{array}{cc}\hfill & X_0:f_{\varphi }\left(w_{1,1}\right)<\cdots <f_{\varphi }\left(w_{\xi ,c_1}\right)<f_{\varphi }\left(w_{\alpha ,c}\right)<\cdots <f_{\varphi }\left(w_{m,2}\right)\hfill \\ \hfill & Y_0:f_{\varphi }\left(w_{1,3}\right)<\cdots <f_{\varphi }\left(w_{\beta ,d-1}\right)<f_{\varphi }\left(w_{\beta ,d}\right)<\cdots <f_{\varphi }\left(w_{m,n}\right).\hfill \end{array}$(20) ) and (23(23) $\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}<\overline{f_{\varphi }\left(w_{\beta ,d}\right)}.$(23) ) it can be obtained that (24) $\left\{\begin{array}{cc}\hfill & \cdots <f_{\varphi }\left(w_{\xi ,c_1}\right)<\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}<\overline{f_{\varphi }\left(w_{\beta ,d}\right)}<f_{\varphi }\left(w_{\beta ,d}\right)=f_{\varphi }\left(w_{\alpha ,c}\right)<\cdots \hfill \\ \hfill & \cdots <f_{\varphi }\left(w_{\beta ,d-1}\right)<\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}<\overline{f_{\varphi }\left(w_{\beta ,d}\right)}<f_{\varphi }\left(w_{\beta ,d}\right)<\cdots \hfill \end{array}\right.$(24) By comparing (20(20) $\begin{array}{cc}\hfill & X_0:f_{\varphi }\left(w_{1,1}\right)<\cdots <f_{\varphi }\left(w_{\xi ,c_1}\right)<f_{\varphi }\left(w_{\alpha ,c}\right)<\cdots <f_{\varphi }\left(w_{m,2}\right)\hfill \\ \hfill & Y_0:f_{\varphi }\left(w_{1,3}\right)<\cdots <f_{\varphi }\left(w_{\beta ,d-1}\right)<f_{\varphi }\left(w_{\beta ,d}\right)<\cdots <f_{\varphi }\left(w_{m,n}\right).\hfill \end{array}$(20) ) with (24(24) $\left\{\begin{array}{cc}\hfill & \cdots <f_{\varphi }\left(w_{\xi ,c_1}\right)<\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}<\overline{f_{\varphi }\left(w_{\beta ,d}\right)}<f_{\varphi }\left(w_{\beta ,d}\right)=f_{\varphi }\left(w_{\alpha ,c}\right)<\cdots \hfill \\ \hfill & \cdots <f_{\varphi }\left(w_{\beta ,d-1}\right)<\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}<\overline{f_{\varphi }\left(w_{\beta ,d}\right)}<f_{\varphi }\left(w_{\beta ,d}\right)<\cdots \hfill \end{array}\right.$(24) ) it can be obtained that there is no element in $X_0$ and $Y_0$ being equal to $\overline{f_{\varphi }\left(w_{\beta ,d}\right)}$ or $\overline{f_{\varphi }\left(w_{\beta ,d-1}\right)}$.

Fig. 4 Antimagic labeling of $P_m\left[P_2\right]$.

Notes

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11401430 and 11301381).

Peer review under responsibility of Kalasalingam University.