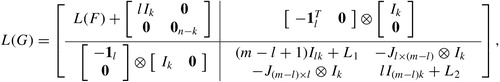Results on Laplacian spectra of graphs with pockets

Peer review under responsibility of Kalasalingam University.

Abstract

Let $F,H_v$ be simple connected graphs on $n$ and $m+1$ vertices, respectively. Let $v$ be a specified vertex of $H_v$ and $u_1,\dots ,u_k\in F$. Then the graph $G=G[F,u_1,\dots ,u_k,H_v]$ obtained by taking one copy of $F$ and $k$ copies of $H_v,$ and then attaching the $i$th copy of $H_v$ to the vertex $u_i$, $i=1,\dots ,k$, at the vertex $v$ of $H_v$ (identify $u_i$ with the vertex $v$ of the $i$th copy) is called a graph with $k$ pockets. In 2008, Barik raised the question that ‘how far can the Laplacian spectrum of $G$ be described by using the Laplacian spectra of $F$ and $H_v$?’ and discussed the case when $\mathrm{deg}\left(v\right)=m$ in $H_v$. In this article, we study the problem for more general cases and describe the Laplacian spectrum. As an application, we construct new nonisomorphic Laplacian cospectral graphs from the known ones.

Keywords:

• Laplacian matrix
• Laplacian spectrum
• Join
• Pockets

1 Introduction

Throughout this article we consider only simple graphs. Let $G=(V\left(G\right),E\left(G\right))$ be a graph with vertex set $V\left(G\right)=\{1,2,\dots ,n\}$ and edge set $E\left(G\right)$. The adjacency matrix of $G$, denoted by $A\left(G\right)$, is the $n\times n$ matrix whose $(i,j)$-th entry is $1$, if $i$ and $j$ are adjacent in $G$ and $0$, otherwise. The Laplacian matrix of $G$ is defined as $L\left(G\right)=D\left(G\right)-A\left(G\right)$, where $D\left(G\right)$ is the diagonal degree matrix of $G.$ It is well known that $L\left(G\right)$ is a symmetric positive semidefinite matrix. Throughout this paper the Laplacian spectrum of $G$ is defined as $\sigma \left(G\right)=({\lambda }_1\left(G\right),{\lambda }_2\left(G\right),\dots ,{\lambda }_n\left(G\right)),$ where ${\lambda }_1\left(G\right)\le {\lambda }_2\left(G\right)\le \cdots \le {\lambda }_n\left(G\right)$ are the eigenvalues of $L\left(G\right)$ arranged in nondecreasing order. For any graph $G,$ ${\lambda }_1\left(G\right)=0$ and is afforded by the all ones eigenvector $\mathbf{1}.$ There is an extensive literature on works related to Laplacian matrices and their spectra. Interested readers are referred to [1,2] and the references therein.

Two graphs are said to be Laplacian cospectral if they share same Laplacian spectrum. Haemers and Spence [3] enumerated the numbers for which there are at least two graphs with the same Laplacian spectrum and gave some techniques for their construction.

From literature we find many operations defined on graphs such as disjoint union, complement, join, graph products (Cartesian product, direct product, strong product, lexicographic product, etc.), corona and many variants of corona (like edge corona, neighborhood corona, edge neighborhood corona, etc.). For such operations often it is possible to describe the Laplacian spectrum of the resulting graph using the Laplacian spectra of the corresponding constituting graphs, see [4,5] for reference. This enables one to visualize a complex network in terms of small simple recognizable graphs whose Laplacian spectra is easily computable. It is always interesting for researchers in spectral graph theory to define some new graph operations such that the Laplacian spectra of the new graphs produced can be described using the Laplacian spectra of the constituent graphs.

If $F=(V\left(F\right),E\left(F\right))$ and $H=(V\left(H\right),E\left(H\right))$ are two graphs on disjoint sets of $m$ and $n$ vertices, respectively, their union is the graph $F+H=(V\left(F\right)\cup V\left(H\right),E\left(F\right)\cup E\left(H\right))$, and their join is $F\vee H={(F^c+H^c)}^c$, the graph on $m+n$ vertices obtained from $F+H$ by adding new edges from each vertex of $F$ to every vertex of $H$. Note that, here $F^c$ denotes the complement graph of the graph $F$.

The following result which describes the Laplacian spectrum of join of two graphs is often used in the next sections.

Theorem 1

[6], Theorem 2.1

Let $F,H$ be graphs on disjoint sets of $m,n,$ vertices respectively, and $G=F\vee H.$ Let $\sigma \left(F\right)=({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_m)$ and $\sigma \left(H\right)=({\mu }_1,{\mu }_2,\dots ,{\mu }_n).$ Then $0,n+{\lambda }_2,\dots ,n+{\lambda }_m,m+{\mu }_2,\dots ,m+{\mu }_n,m+n\in \sigma \left(G\right).$

The following graph operation is defined in [7].

Definition 2

[7]

Let $F,H_v$ be connected graphs, $v$ be a specified vertex of $H_v$ and $u_1,\dots ,u_k\in F$. Let $G=G[F,u_1,\dots ,u_k,H_v]$ be the graph obtained by taking one copy of $F$ and $k$ copies of $H_v$, and then attaching the $i$th copy of $H_v$ to the vertex $u_i,i=1,\dots ,k,$ at the vertex $v$ of $H_v$ (identify $u_i$ with the vertex $v$ of the $i$th copy). Then the copies of the graph $H_v$ that are attached to the vertices $u_i,i=1,\dots ,k$ are referred to as pockets, and $G$ is described as a graph with pockets.

Suppose that $F$ and $H_v$ are graphs on $n$ and $m+1$ vertices, respectively. Using the above operation, we can produce many interesting classes of graphs. Since the operation is a very general operation, in [7], the author has asked the question that ‘how far can the Laplacian spectrum of $G$ be described by using the Laplacian spectra of $F$ and $H_v$?’. In that paper, the author has described the Laplacian spectrum of $G$ using the Laplacian spectra $F$ and $H_v$ in a particular case when $deg\left(v\right)=m$. This motivates us for studying the Laplacian spectrum of more such graphs relaxing condition that $deg\left(v\right)=m$. Let $deg\left(v\right)=l,1\le l\le m$. In this case, we denote $G[F,u_1,\dots ,u_k,H_v]$ more precisely by $G[F,u_1,\dots ,u_k;H_v,l]$. When $k=n$, we denote $G=G[F,u_1,\dots ,u_k;H_v,l]$ simply by $G[F;H_v,l]$.

Let $H=H_v\setminus \left\{v\right\}$. When $deg\left(v\right)=m$, we have $H_v=\left\{v\right\}\vee H$. Now using Theorem 1, the Laplacian spectrum of $H_v$ can be obtained from that of $H$. So the question of describing the Laplacian spectrum of $G$ in terms of the Laplacian spectra of $F$ and $H_v$ is same as asking for the description of the Laplacian spectrum of $G$ in terms of the Laplacian spectra of $F$ and $H$. Further, when $l=m$ and $k=n$, we have $G[F;H_v,m]=F\circ H$, the corona of $F$ and $H$ (see [8]). In [9], the Laplacian spectrum of $F\circ H$ has been completely described using the Laplacian spectra of $F$ and $H$.

Now if $deg\left(v\right)=l,1\le l\le m$, let $N\left(v\right)=\{v_1,v_2,\dots ,v_l\}\subset V\left(H_v\right)$, be the neighborhood set of $v$ in $H_v$. Let $H_1$ be the subgraph of $H_v$ induced by the vertices in $N\left(v\right)$ and $H_2$ be the subgraph of $H_v$ induced by the vertices which are in $V\left(H_v\right)\setminus (N\left(v\right)\cup \left\{v\right\})$. When $H_v=H_1\vee (H_2+\left\{v\right\})$, we describe the complete Laplacian spectrum of $G[F;H_v,l]$ using that of $F$ and $H$. The results are contained in Section 2 of the article.

Further, except $n+2k$ eigenvalues, we describe all other eigenvalues of $G[F,u_1,\dots ,u_k;H_v,l]$ and prove that the remaining $n+2k$ eigenvalues are independent of the graphs $H_1$ and $H_2$. In particular, when $F=F_1\vee F_2$, where $F_1$ is the subgraph of $F$ induced by the vertices $u_1,\dots ,u_k$, we describe the complete Laplacian spectrum of $G[F,u_1,\dots ,u_k;H_v,l]$. These results are contained in Section 3.

Following notations are being used in rest of the paper. The $n\times 1$ vector with each entry $0$ is denoted by ${\mathbf{0}}_n$. The Kronecker product of matrices $R=\left[r_{ij}\right]\text{and}S$ is defined to be the partitioned matrix $\left[r_{ij}S\right]$ and is denoted by $R\otimes S.$ The vector with $i$th entry equal to $1$ and all other entries zero is denoted by $e_i$. By $J_{n\times m}$ we denote the matrix of order $n\times m$ whose entries are all equal to $1$. If $n=m$, we write $J_{n\times m}$ simply by $J_n$. By $I_n$ we denote the identity matrix of size $n$. We avoid writing the order of these matrices if it is clear from the context. $K_n$ and $C_n$ denote the complete graph and cycle graph of order $n$, respectively.

2 Laplacian spectrum of $[F;H_v,l]$

Let $F$ be a connected graph with vertex set $\{u_1,u_2,\dots ,u_n\}$. Let $H_v$ be a connected graph on $m+1$ vertices with a specified vertex $v$ and $V\left(H_v\right)=\{v_1,v_2,\dots ,v_m,v\}$. Let $G=G[F;H_v,l]$. Note that $G$ has $n(m+1)$ vertices.

Let $deg\left(v\right)=l,1\le l\le m$. Without loss of generality assume that $N\left(v\right)=\{v_1,v_2,\dots ,v_l\}$. Let $H_1$ be the subgraph of $H_v$ induced by the vertices $\{v_1,v_2,\dots ,v_l\}$ and $H_2$ be the subgraph of $H_v$ induced by the vertices $\{v_{l+1},v_{l+2},\dots ,v_m\}$. Suppose that $H_v=H_1\vee (H_2+\left\{v\right\})$.

Let $v_j^i$ denote the $j$th vertex of $H_v$ in the $i$th copy of $H_v$ in $G$, for $i=1,2,\dots ,n;j=1,2,\dots ,m$, and let $V_j\left(H_v\right)=\{v_j^1,v_j^2,\dots ,v_j^n\}$. Then $V\left(F\right)\cup \left({\cup }_{j=1}^m{V}_j\left(H_v\right)\right)$ is a partition of $V\left(G\right)$. Using this partition, the Laplacian matrix of $G=G[F;H_v,l]$ can be expressed as $L\left(G\right)=\left[\begin{array}{ccc}\hfill L\left(F\right)+l{I}_n\hfill & \hfill -{\mathbf{1}}_l^T\otimes I_n\hfill & \hfill \mathbf{0}\hfill \\ \hfill -{\mathbf{1}}_l\otimes I_n\hfill & \hfill \left(L\left(H_1\right)+(m-l+1)I_l\right)\otimes I_n\hfill & \hfill -J_{l\times (m-l)}\otimes I_n\hfill \\ \hfill \mathbf{0}\hfill & \hfill -J_{(m-l)\times l}\otimes I_n\hfill & \hfill \left(L\left(H_2\right)+l{I}_{m-l}\right)\otimes I_n\hfill \end{array}\right].$

The following is one of the main results of this article, which describes the complete Laplacian spectrum of $G[F;H_v,l]$ using that of $F$ and $H_v$.

Theorem 3

Let $F$ be a connected graph on $n$ vertices and $H_v$ be a graph on $m+1$ vertices $\{v_1,v_2,\dots ,v_m,v\}$, with a specified vertex $v$ with degree $l,1\le l\le m$. Let $N\left(v\right)=\{v_1,v_2,\dots ,v_l\}$ and $H_1$ be the subgraph of $H_v$ induced by the vertices $\{v_1,v_2,\dots ,v_l\}$and $H_2$ be the subgraph of $H_v$ induced by the vertices $\{v_{l+1},v_{l+2},\dots ,v_m\}$. Suppose that $H_v=H_1\vee (H_2+\left\{v\right\})$. Let $\sigma \left(F\right)=(0={\beta }_1,{\beta }_2,\dots ,{\beta }_n)$, $\sigma \left(H_1\right)=(0={\mu }_1,{\mu }_2,\dots ,{\mu }_l)$ and $\sigma \left(H_2\right)=(0={\nu }_1,{\nu }_2,\dots ,{\nu }_{m-l}).$ Then the Laplacian spectrum of $G=G[F;H_v,l]$ consists of

(i)	the roots of the equation ${\lambda }^3-{\lambda }^2({\beta }_i+l+m+1)+\lambda \left({\beta }_i+l\right)(m+1)-l{\beta }_i=0,$for $i=1,2,\dots ,n$;

(ii)	${\mu }_j+m-l+1$ with multiplicity at least $n$, for $j=2,\dots ,m-l$; and

(iii)

${\nu }_j+l$ with multiplicity at least $n$, for $j=2,\dots ,l$.

Proof

To prove part (i), suppose that $x_1,x_2,\dots ,x_n$ are the eigenvectors of $L\left(F\right)$ corresponding to the eigenvalue ${\beta }_1,{\beta }_2,\dots ,{\beta }_n$, respectively. Now for $i=1,2,\dots ,n$, consider a vector of the form $X=\left(\begin{array}{c}\hfill k_1{x}_i\hfill \\ \hfill {\mathbf{1}}_l\otimes x_i\hfill \\ \hfill k_2{\mathbf{1}}_{m-l}\otimes x_i\hfill \end{array}\right),$where $k_1$ and $k_2$ are two arbitrary constants. $X$ is an eigenvector of $L\left(G\right)$ corresponding to an eigenvalue $\lambda$ (say) if and only if it satisfies the equation $L\left(G\right)X=\lambda X$, which gives the following system of equations $k_1({\beta }_i+l)-l=k_1\lambda ,-k_1+m-l+1-k_2(m-l)=\lambda ,-l+k_{2}l=k_2\lambda .$ Eliminating $k_1$ and $k_2$, we get ${\lambda }^3-{\lambda }^2({\beta }_i+l+m+1)+\lambda \left({\beta }_i+l\right)(m+1)-l{\beta }_i=0.$Hence part (i) follows.

To prove part (ii) and (iii), let ${\mathbf{1}}_l,y_2,\dots ,y_l$ be the eigenvectors of $L\left(H_1\right)$ corresponding to the eigenvalues ${\mu }_1,{\mu }_2,\dots ,{\mu }_l$, respectively. Similarly, let ${\mathbf{1}}_{m-l},z_2,\dots ,z_{m-l}$ be the eigenvectors of $L\left(H_2\right)$ corresponding to the eigenvalues ${\nu }_1,{\nu }_2,\dots ,{\nu }_{m-l}$, respectively. Note that, for $j=2,3,\dots ,l$ and $p=2,3,\dots ,m-l$, $y_j$ and $z_p$ are orthogonal to ${\mathbf{1}}_l$ and ${\mathbf{1}}_{m-l}$, respectively. Hence for $i=1,2,\dots ,n$; $j=2,3,\dots ,l$; $p=2,3,\dots ,m-l$; $\left(\begin{array}{c}\hfill {\mathbf{0}}_n\hfill \\ \hfill y_j\otimes e_i\hfill \\ \hfill {\mathbf{0}}_{n(m-l)}\hfill \end{array}\right)\text{and}\left(\begin{array}{c}\hfill {\mathbf{0}}_n\hfill \\ \hfill {\mathbf{0}}_{ln}\hfill \\ \hfill z_p\otimes e_i\hfill \end{array}\right)$are eigenvectors of $L\left(G\right)$ corresponding to the eigenvalues ${\mu }_j+m-l+1$ and ${\nu }_p+l$, respectively. Hence the proof.  □

The following example illustrates the above theorem.

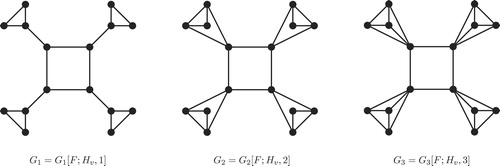
Example 4

Consider the graphs $F=C_4$ and $H=C_3$. Taking $l=1,2$ and $3$, we have graphs $G_1=G_1[F;H_v,1],G_2=G_1[F;H_v,2]$, and $G_3=G_1[F;H_v,3]$, respectively. See Fig. 1. It can be checked that $\sigma \left(F\right)=(0,2^{\left(2\right)},4)$ and $\sigma \left(H_v\right)=(0,1,3,4)$, where the exponents within parenthesis indicate the multiplicities (number of occurrence) of the corresponding eigenvalues. Then the Laplacian spectrum of $G_i,i=1,2,3,$ are (computed through a matlab program) $\sigma \left(G_1\right)=(0,0.1864^{\left(2\right)},0.2215,1,2.4707^{\left(2\right)},3^{\left(4\right)},3.2892,4,4.3429^{\left(2\right)},5.4893);\sigma \left(G_2\right)=(0,0.2907^{\left(2\right)},0.3961,2,2.8061^{\left(2\right)},3.1099,4^{\left(5\right)},4.9032^{\left(2\right)},6.4940);\sigma \left(G_3\right)=(0,0.3542^{\left(2\right)},0.5359,4^{\left(9\right)},5.6458^{\left(2\right)},7.4641).$

One can check that $\sigma \left(G_i\right),i=1,2,3$ matches with that obtained using the above theorem.

Fig. 1 $[F;H_v,l]$ for different $l$.

Remark 5

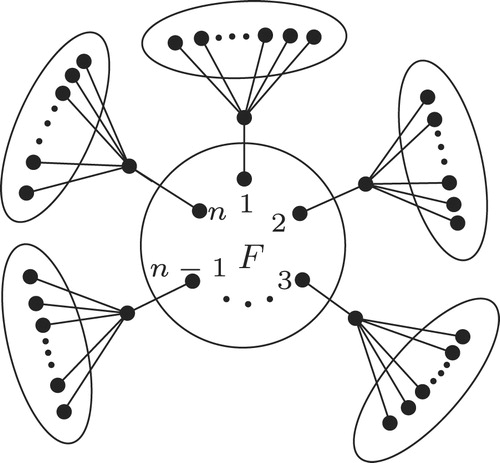
In a particular case, if we take $H_1=K_1$ and $H_2=(m-1)K_1$, the empty graph on $m-1$ vertices (in Theorem 3), we will get an interesting class of graphs. See Fig. 2. Notice that this class is nothing but the class of graphs obtained by taking a graph $F$ on $n$ vertices and then taking $n$ copies of a star on $m+1$ vertices and attaching one pendant vertex of $i$th copy of the star to the $i$th vertex of $F$. The complete Laplacian spectra of these graphs can be described easily using Theorem 3.

Fig. 2 A graph with pockets as stars.

Remark 6

As ${\beta }_1=0$, substituting the value in the equation given in Theorem 3 (ii), we get ${\lambda }^3-{\lambda }^2(m+l+1)+\lambda l(m+1)=0$ whose roots are $0,l$ and $m+1$. So $l$ is always an eigenvalue of $L\left(G[F;H_v,l]\right)$, with corresponding eigenvector $\left(\begin{array}{c}\hfill (l-m){\mathbf{1}}_n\hfill \\ \hfill {\mathbf{0}}_{ln}\hfill \\ \hfill {\mathbf{1}}_{(m-l)n}\hfill \end{array}\right).$

Remark 7

In Theorem 3, $H_v=H_1\vee (H_2+\left\{v\right\})$. Since $\sigma \left(H_1\right)=(0={\mu }_1,{\mu }_2,\dots ,{\mu }_l)$ and $\sigma \left(H_2\right)=(0={\nu }_1,{\nu }_2,\dots ,{\nu }_{m-l})$, we have $\sigma (H_2+\left\{v\right\})=(0,0,{\nu }_2,\dots ,{\nu }_{m-l})$. Thus, using Theorem 1, the Laplacian spectrum of $H_v$ consists of the eigenvalues $0;{\mu }_2+m-l+1,\dots ,{\mu }_l+m-l+1;l,{\nu }_2+l,\dots ,{\nu }_{m-l}+l;m+1.$ So, notice that all the eigenvalues of $L\left(H_v\right)$ are also the eigenvalues of $L\left(G\right)$. Further, except $0,l$ and $m+1$, all other eigenvalues of $L\left(H_v\right)$ are of multiplicity at least $n$ in $\sigma \left(G\right)$.

The following is auseful corollary of Theorem 3 which describes a construction of new Laplacian cospectral graphs from known pairs of nonisomorphic Laplacian cospectral graphs.

Corollary 8

Let $(F,\widehat{F}),(H_1,{\widehat{H}}_1)$ and $(H_2,{\widehat{H}}_2)$ are pairs of nonisomorphic Laplacian cospectral graphs on $n,l$ and $m-l$ vertices, respectively. Construct the graphs $H_v$ and ${\widehat{H}}_{\hat{v}}$ on $m+1$ vertices such that $H_v=H_1\vee (H_2+\left\{v\right\})$ and ${\widehat{H}}_{\hat{v}}={\widehat{H}}_1\vee ({\widehat{H}}_2+\left\{\hat{v}\right\})$. Then the graphs $G=G[F;H_v,l]$ and $\widehat{G}=\widehat{G}[\widehat{F};{\widehat{H}}_v,l]$ are Laplacian cospectral, when $(F,\widehat{F})$ and $(H_v,{\widehat{H}}_v)$ are pairwise nonisomorphic Laplacian cospectral graphs.

Proof

Proof is immediate from Theorem 3.  □

Remark 9

If $(F,\widehat{F}),(H_1,{\widehat{H}}_1)$ and $(H_2,{\widehat{H}}_2)$ are pairs of nonisomorphic Laplacian cospectral graphs on $n,l$ and $m-l$ vertices, respectively, then by taking different combinations of them one can have at least $2^3-1=7$ nonisomorphic Laplacian cospectral graphs which are Laplacian cospectral to $G[F,H_v,l]$, where $H_v=H_1\vee (H_2+\left\{v\right\})$.

When $H_v$ is not expressible as $H_1\vee (H_2+\left\{v\right\})$ for any $H_1$ and $H_2$, we still can describe some of the Laplacian eigenvalues of $G[F;H_v,l]$.

Theorem 10

Let $F$ be a connected graph on $n$ vertices and $H_v$ be any graph on $m+1$ vertices with a specified vertex $v$. Then the Laplacian spectrum of $H_v$ is contained in the Laplacian spectrum of $G=G[F;H_v,l]$. Furthermore, if $\lambda$ is an eigenvalue of $L\left(H_v\right)$ afforded by an eigenvector $y$ such that its $v$th component, $y\left(v\right)=0$, then $\lambda$ is in the Laplacian spectrum of $G$ occurring at least $n$ times.

Proof

Observe that the Laplacian matrix of $G=G[F;H_v,l]$ can be expressed as $L\left(G\right)=\text{diag}(L\left(F\right),{\mathbf{0}}_{mn})+L\left(H_v\right)\otimes I_n.$Without loss of generality, let us assume that the vertex $v$ be the first vertex of $H_v$. Let $x$ be an eigenvector of $L\left(H_v\right)$ corresponding to an eigenvalue $\alpha$ (say) such that $x\left(1\right)=x\left(v\right)=1$. Let $\tilde{x}={\left(x\left(2\right),\dots ,x(m+1)\right)}^T$. Now it can be observed that $\left(\begin{array}{c}\hfill {\mathbf{1}}_n\hfill \\ \hfill \tilde{x}\otimes {\mathbf{1}}_n\hfill \end{array}\right)$ is an eigenvector of $L\left(G\right)$ corresponding to the eigenvalue $\alpha$.

Finally, if $\lambda$ is an eigenvalue of $L\left(H_v\right)$ afforded by an eigenvector $y$ such that its $v$th component, $y\left(v\right)=0$, then $\left(\begin{array}{c}\hfill {\mathbf{0}}_n\hfill \\ \hfill \tilde{y}\otimes e_i\hfill \end{array}\right)$, for $i=1,\dots ,n$, are the eigenvectors of $L\left(G\right)$ corresponding to the eigenvalue $\lambda$, where $\tilde{y}={\left(y\left(2\right),\dots ,y(m+1)\right)}^T$. Hence the result.  □

3 Laplacian spectrum of a graph with pockets

In this section, we consider the case when $k$ is not necessarily equal to $n$. Let $F$ be a connected graph with vertex set $\{u_1,u_2,\dots ,u_n\}$. Let $H_v$ be a graph on $m+1$ vertices with a specified vertex $v$ and $V\left(H_v\right)=\{v_1,v_2,\dots ,v_m,v\}$. Let $deg\left(v\right)=l,1\le l\le m$. Without loss of generality, assume that $N\left(v\right)=\{v_1,v_2,\dots ,v_l\}$. Let $H_1$ be the subgraph of $H_v$ induced by the vertices $\{v_1,v_2,\dots ,v_l\}$ and $H_2$ be the subgraph of $H_v$ induced by the vertices $\{v_{l+1},v_{l+2},\dots ,v_m\}$. Suppose that $H_v=H_1\vee (H_2+\left\{v\right\})$.

Let $G=G[F,u_1,\dots ,u_k;H_v,l]$ be the graph obtained by taking one copy of $F$ and $k$ copies of $H_v$, and then attaching the $i$th copy of $H_v$ to the vertex $u_i,i=1,\dots ,k,$ at the vertex $v$ of $H_v$ (identify $u_i$ with the vertex $v$ of the $i$th copy). In general, it is difficult to characterize all the Laplacian eigenvalues of $G$. In the following theorem we describe $k(m-2)$ eigenvalues of $L\left(G\right)$ and prove that the remaining $n+2k$ eigenvalues are independent of thegraph $H_v$.

Theorem 11

Let $G=G[F,u_1,\dots ,u_k;H_v,l]$ be the graph as described above. Suppose that $\sigma \left(H_1\right)=(0={\mu }_1,{\mu }_2,\dots ,{\mu }_l)$, $\sigma \left(H_2\right)=(0={\nu }_1,{\nu }_2,\dots ,{\nu }_{m-l})$. Let $\widehat{G}=\widehat{G}[F,u_1,\dots ,u_k;{\widehat{H}}_v,l]$, where ${\widehat{H}}_v=l{K}_1\vee \left((m-l)K_1+\left\{v\right\}\right)$. Then ${\mu }_j+m-l+1$ for $j=2,\dots ,m-l$ and ${\nu }_p+l$ for $p=2,\dots ,l$ are eigenvalues of $L\left(G\right)$ each of multiplicity $k$, and the other $n+2k$ eigenvalues are independent of the graph $H_v$. That is, if

(i)	$m-l+1\in \sigma \left(\widehat{G}\right)$ with multiplicity $k(m-l-1)$,

(ii)	$l\in \sigma \left(\widehat{G}\right)$ with multiplicity $k(l-1)$ and

(iii)

${\alpha }_i\in \sigma \left(\widehat{G}\right)$, for $i=1,\dots ,n+2k$;

then

(i)	${\mu }_j+m-l+1\in \sigma \left(G\right)$ with multiplicity $k$ for $j=2,\dots ,m-l$,

(ii)	${\nu }_j+l\in \sigma \left(G\right)$ with multiplicity $k$, for $j=2,\dots ,l$ and

(iii)

${\alpha }_i\in \sigma \left(G\right)$, for $i=1,\dots ,n+2k$.

Proof

The Laplacian matrix of $G=G[F,u_1,\dots ,u_k;H_v,l]$ can be expressed as where $L_1=L\left(H_1\right)\otimes I_k$ and $L_2=L\left(H_2\right)\otimes I_k$. So the Laplacian matrix of $\widehat{G}=\widehat{G}[F,u_1,\dots ,u_k;{\widehat{H}}_v,l]$ can be related to $L\left(G\right)$ as $L\left(G\right)=L\left(\widehat{G}\right)+\text{diag}({\mathbf{0}}_n,L_1,L_2).$Now, suppose that ${\mathbf{1}}_l,y_2,\dots ,y_l$ are the eigenvectors of $L\left(H_1\right)$ corresponding to the eigenvalues ${\mu }_1,{\mu }_2,\dots ,{\mu }_l$, respectively. Similarly, let ${\mathbf{1}}_{m-l},z_2,\dots ,z_{m-l}$ be the eigenvectors of $L\left(H_2\right)$ corresponding to the eigenvalues ${\nu }_1,{\nu }_2,\dots ,{\nu }_{m-l}$, respectively. Then observe that for $i=1,2,\dots ,k$; $j=2,3,\dots ,l$; $p=2,3,\dots ,m-l$, $\left(\begin{array}{c}\hfill {\mathbf{0}}_n\hfill \\ \hfill y_j\otimes e_i\hfill \\ \hfill {\mathbf{0}}_{k(m-l)}\hfill \end{array}\right)\text{and}\left(\begin{array}{c}\hfill {\mathbf{0}}_n\hfill \\ \hfill {\mathbf{0}}_{lk}\hfill \\ \hfill z_p\otimes e_i\hfill \end{array}\right)$are eigenvectors of $L\left(G\right)$ corresponding to the eigenvalues ${\mu }_j+m-l+1$ and ${\nu }_p+l$, respectively. Similarly, for $i=1,2,\dots ,k$; $j=2,3,\dots ,l$; $p=2,3,\dots ,m-l$, $\left(\begin{array}{c}\hfill {\mathbf{0}}_n\hfill \\ \hfill (e_1-e_j)\otimes e_i\hfill \\ \hfill {\mathbf{0}}_{k(m-l)}\hfill \end{array}\right)\text{and}\left(\begin{array}{c}\hfill {\mathbf{0}}_n\hfill \\ \hfill {\mathbf{0}}_{kl}\hfill \\ \hfill (e_1-e_p)\otimes e_i\hfill \end{array}\right)$are eigenvectors of $L\left(\widehat{G}\right)$ corresponding to the eigenvalues $m-l+1$ and $l$, respectively. Furthermore, by choosing vectors of the form $\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill k_1{\mathbf{1}}_l\otimes x\hfill \\ \hfill k_2{\mathbf{1}}_{m-l}\otimes x\hfill \end{array}\right),$for some $k_1,k_2$, we get the same set of eigen-equations for $L\left(G\right)$ and $L\left(\widehat{G}\right)$. Hence the result follows.  □

Now, consider the case when $F=F_1\vee F_2$, where $F_1$ is the subgraph of $F$ induced by the vertices $u_1,\dots ,u_k$ and $F_2$ is the subgraph of $F$ induced by the vertices $u_{k+1},\dots ,u_n$. In this case, we describe the Laplacian matrix and the complete Laplacian spectrum of $G[F,u_1,\dots ,u_k;H_v,l]$.

Let $v_j^i$ denote the $j$th vertex of $H_v$ in the $i$th copy of $H_v$ in $G$, for $i=1,2,\dots ,k;j=1,2,\dots ,m$, and let $V_j\left(H_v\right)=\{v_j^1,v_j^2,\dots ,v_j^k\}$. Then $V\left(F_1\right)\cup V\left(F_2\right)\cup \left({\cup }_{j=1}^m{V}_j\left(H_v\right)\right)$ is a partition of the vertex set of $G=G[F,u_1,\dots ,u_k;H_v,l]$. Using this partition, the Laplacian matrix of $G$ can be expressed as $L\left(G\right)=\left[\begin{array}{cccc}\hfill L_1\hfill & \hfill -J_{k\times (n-k)}\hfill & \hfill -{\mathbf{1}}_l^T\otimes I_k\hfill & \hfill \mathbf{0}\hfill \\ \hfill -J_{(n-k)\times k}\hfill & \hfill L_2\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill -{\mathbf{1}}_l\otimes I_k\hfill & \hfill \mathbf{0}\hfill & \hfill L_3\hfill & \hfill -J_{l\times (m-l)}\otimes I_k\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill -J_{(m-l)\times l}\otimes I_k\hfill & \hfill L_4\hfill \end{array}\right],$where $L_1=L\left(F_1\right)+(n-k+l)I_k,L_2=L\left(F_2\right)+k{I}_{n-k},L_3=(L\left(H_1\right)+(m-l+1)I_l)\otimes I_k$, and $L_4=(L\left(H_2\right)+l{I}_{m-l})\otimes I_k.$

The following result describes the complete Laplacian spectrum of $G[F,u_1,\dots ,u_k;H_v,l]$.

Theorem 12

Let $G=G[F,u_1,\dots ,u_k;H_v,l]$ be the graph as described above. Let $\sigma \left(F_1\right)=(0={\alpha }_1,{\alpha }_2,\dots ,{\alpha }_k)$, $\sigma \left(F_2\right)=(0={\beta }_1,{\beta }_2,\dots ,{\beta }_{n-k})$, $\sigma \left(H_1\right)=(0={\mu }_1,{\mu }_2,\dots ,{\mu }_l)$, and $\sigma \left(H_2\right)=(0={\nu }_1,{\nu }_2,\dots ,{\nu }_{m-l})$. Then the Laplacian spectrum of $G$ consists of the eigenvalues as

(i)

$0$;

(ii)	the roots of the equation ${\lambda }^3-{\lambda }^2(m+n+l+1)+\lambda \left(l(m+k+1)+n(m+1)\right)-l(n+mk)=0;$

(iii)

for $i=2,3,\dots ,k$, the roots of the equation ${\lambda }^3-{\lambda }^2({\alpha }_i+n-k+l+m+1)+\lambda ({\alpha }_i+n-k+l)(m+1)-l({\alpha }_i+n-k)=0;$

(iv)	${\beta }_2+k,\dots ,{\beta }_{n-k}+k$; and

(v)	${\mu }_j+m-l+1$ and ${\nu }_p+l$ for $i=2,3,\dots ,l$ and $p=2,3,\dots ,m-l$, each with multiplicity at least $k$.

Proof

Proof of part (i) is trivial.

To prove part (ii), consider the vector $X=\left(\begin{array}{c}\hfill {\mathbf{1}}_k\hfill \\ \hfill k_1{\mathbf{1}}_{n-k}\hfill \\ \hfill k_2{\mathbf{1}}_l\otimes {\mathbf{1}}_k\hfill \\ \hfill k_3{\mathbf{1}}_{m-l}\otimes {\mathbf{1}}_k\hfill \end{array}\right),$ where $k_1,k_2$ and $k_3$ are some arbitrary constants. Then $X$ would be an eigenvector for $L\left(G\right)$ if it satisfies the matrix equation $L\left(G\right)X=\lambda X$ for some $\lambda$, which after simplification gives the following system of equations $n-k+l-k_1(n-k)-k_{2}l=\lambda ,-k+k_{1}k=k_1\lambda ,-1+k_2(1+m-l)-k_3(m-l)=k_2\lambda ,-l{k}_2+k_{3}l=k_3\lambda ,$ in $4$ unknowns $k_1,k_2,k_3$ and $\lambda$. Now eliminating $k_1,k_2$ and $k_3$, we get ${\lambda }^4-{\lambda }^3(m+n+l+1)+{\lambda }^2\left(l(m+k+1)+n(m+1)\right)-\lambda l(n+mk)=0.$Hence we get result (ii).

To prove (iii), suppose that ${\mathbf{1}}_k,x_2,\dots ,x_k$ are the eigenvectors of $L\left(F\right)$ corresponding to the eigenvalues ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_k$, respectively. Now for $i=2,\dots ,k$, consider the vectors $X_i=\left(\begin{array}{c}\hfill k_1{x}_i\hfill \\ \hfill {\mathbf{0}}_{n-k}\hfill \\ \hfill {\mathbf{1}}_l\otimes x_i\hfill \\ \hfill k_2{\mathbf{1}}_{m-l}\otimes x_i\hfill \end{array}\right),$where $k_1$ and $k_2$ are two arbitrary constants. From the eigen-equations, we have $k_1({\alpha }_i+n-k+l)-k_{2}l=k_1\lambda ,-k_1+k_2(m-l+1)-(m-l)=\lambda ,-k_{2}l+l=k_2\lambda .$ Then solving the above equations for $\lambda$, we have the required result.

To prove (iv), suppose that ${\mathbf{1}}_{n-k},{\widehat{x}}_2,\dots ,{\widehat{x}}_{n-k}$ are eigenvectors of $L\left(F_2\right)$ corresponding to the eigenvalues ${\beta }_1,{\beta }_2,\dots ,{\beta }_{n-k}$, respectively. Consider the vectors $\widehat{X_i}=\left(\begin{array}{c}\hfill {\mathbf{0}}_k\hfill \\ \hfill {\widehat{x}}_i\hfill \\ \hfill {\mathbf{0}}_{lk}\hfill \\ \hfill {\mathbf{0}}_{(m-l)k}\hfill \end{array}\right),$for $i=2,3,\dots ,n-k$. Now using Theorem 1, it can be observed that $X_i$ is an eigenvector of $L\left(G\right)$ corresponding to the eigenvalue ${\beta }_i+k$, for $i=2,\dots ,n-k$. Hence the proof.

Proof of part (v) follows directly from parts (ii) and (iii) of Theorem 3.  □

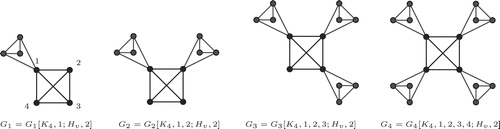
Example 13

Consider the four graphs $G_1,G_2,G_3$ and $G_4$ shown in Fig. 3, obtained from the two graphs $F=K_4$ and $H_v$ such that $H_v\setminus \left\{v\right\}=K_3$. Observe that, $G_1$ has one pocket and in this case $F_1=K_1,F_2=K_3$ and $F=K_1\vee K_3$. Similarly, $G_2$, $G_3$ and $G_4$ are graphs with $2$, $3$, and $4$ pockets, respectively.

It can be checked that $\sigma \left(F\right)=(0,4^{\left(3\right)})$ and $\sigma \left(H_v\right)=(0,2,4^{\left(2\right)})$ and $\sigma \left(G_1\right)=(0,0.7269,3.1404,4^{\left(3\right)},6.1326);\sigma \left(G_2\right)=(0,0.3961,1.0968,3.1099,3.1939,4^{\left(3\right)},5.7093,6.4940);\sigma \left(G_3\right)=(0,0.3961^{\left(2\right)},1.5188,3.1099^{\left(2\right)},3.3111,4^{\left(3\right)},5.1701,6.4940^{\left(2\right)});\sigma \left(G_4\right)=(0,0.3961^{\left(3\right)},2,3.1099^{\left(3\right)},4^{\left(5\right)},6.4940^{\left(3\right)}).$ Notice that $\sigma \left(G_i\right),i=1,\dots ,4$ matches with that obtained as described in the above theorem.

Fig. 3 Graphs having different number of pockets.

Remark 14

Let ${\lambda }_F\in \sigma \left(F\right).$ Now (iii) and (iv) of Theorem 12 can be stated in terms of ${\lambda }_F$ as follows. If ${\lambda }_F-n+k\in \sigma \left(F_1\right)$, then all the roots of ${\lambda }^3-{\lambda }^2({\lambda }_F+l+m+1)+\lambda ({\lambda }_F+l)(m+1)-l{\lambda }_F=0$belong to $\sigma \left(G\right)$. Furthermore, if ${\lambda }_F-k\in \sigma \left(F_2\right)$, then ${\lambda }_F\in \sigma \left(G\right)$.

The following corollary gives a construction of new Laplacian cospectral graphs from the known ones.

Corollary 15

Let $(F_1,{\widehat{F}}_1),(F_2,{\widehat{F}}_2),(H_1,{\widehat{H}}_1)$ and $(H_2,{\widehat{H}}_2)$ be pairs of nonisomorphic Laplacian cospectral graphs on $k,n-k,l$ and $m-l$ vertices, respectively. Let $F=F_1\vee F_2$, $\widehat{F}={\widehat{F}}_1\vee {\widehat{F}}_2$, $H_v=H_1\vee (H_2+\left\{v\right\})$ and ${\widehat{H}}_{\hat{v}}={\widehat{H}}_1\vee ({\widehat{H}}_2+\left\{\hat{v}\right\})$. Let $V\left(F_1\right)=\{u_1,u_2,\dots ,u_k\}$ and $V\left({\widehat{F}}_1\right)=\{{\hat{u}}_1,{\hat{u}}_2,\dots ,{\hat{u}}_k\}$. Then the graphs $G=G[F,u_1,\dots ,u_k;H_v,l]$ and $\widehat{G}=\widehat{G}[\widehat{F},{\hat{u}}_1,\dots ,{\hat{u}}_k;{\widehat{H}}_{\hat{v}},l]$ (each with $k$ pockets) are Laplacian cospectral.

Proof

Proof follows from Theorem 12.  □

Notes

Peer review under responsibility of Kalasalingam University.