Some properties of 2-absorbing primary ideals in lattices

Peer review under responsibility of Kalasalingam University.

Abstract

We introduce the concepts of a primary and a 2-absorbing primary ideal and the radical of an ideal in a lattice. We study some properties of these ideals. A characterization for the radical of an ideal to be a primary ideal is given. Also a characterization for an ideal $I$ to be a 2-absorbing primary ideal is proved. Examples and counter examples are given wherever necessary.

Keywords:

• Ideal
• Prime ideal
• Primary ideal
• 2-absorbing ideal
• 2-absorbing primary ideal

1 Introduction

Badawi [1] introduced the concept of a 2-absorbing ideal in a commutative ring. A proper ideal $I$ of a commutative ring $R$ is said to be a 2-absorbing ideal, if whenever $a,b,c\in R$, $abc\in I$, then either $ab\in I$ or $ac\in I$ or $bc\in I$. Payrovi and Babaei [2] extended the concept of 2-absorbing ideals in commutative rings.

Badawi [3] introduced 2-absorbing primary ideals in commutative rings. A proper ideal $I$ of a commutative ring $R$ is said to be a 2-absorbing primary ideal, if whenever $a,b,c\in R$, $abc\in I$, then either $ab\in I$ or $ac\in \sqrt{I}$ or $bc\in \sqrt{I}$. Mustafanasab and Darani [4] extended the concepts of 2-absorbing primary and weakly 2-absorbing primary ideals in commutative rings.

Manjarekar and Bingi [5] introduced 2-absorbing primary elements in multiplicative lattices. They defined, a proper element $q\in L$ to be a 2-absorbing primary if for every $a,b,c\in L,abc\le q$ implies either $ab\le q$ or $bc\le \sqrt{q}$ or $ca\le \sqrt{q}$.

Celikel et al. [6,7] introduced and studied $\varphi$-2-absorbing elements in multiplicative lattices. Let $\varphi :L\to L\cup \varnothing$ be a function. A proper element $q$ of $L$ is said to be a $\varphi$-2-absorbing element of $L$ if whenever $a,b,c\in L$ with $abc\le q$ and $abc\nleqq \varphi \left(q\right)$ implies either $ab\le q$ or $ac\le q$ or $bc\le q$. Celikel et al. [7] introduced $\varphi$-2-absorbing primary elements in multiplicative lattices as a generalization of $\varphi$-2-absorbing elements. Let $\varphi :L\to L\cup \varnothing$ be a function. A proper element $q$ of $L$ is said to be a $\varphi$-2-absorbing primary element of $L$ if whenever $a,b,c\in L$ with $abc\le q$ and $abc\nleqq \varphi \left(q\right)$ implies either $ab\le q$ or $ac\le \sqrt{q}$ or $bc\le \sqrt{q}$.

Wasadikar and Gaikwad [8] introduced the concept of a 2-absorbing ideal in a lattice. A proper ideal $I$ of a lattice $L$ is said to be a 2-absorbing ideal, if whenever $a,b,c\in L$, $a\wedge b\wedge c\in I$, then either $a\wedge b\in I$ or $a\wedge c\in I$ or $b\wedge c\in I$.

In this paper we introduce the concepts of the radical of an ideal (denoted by $\sqrt{I}$), the primary ideal and the 2-absorbing primary ideal in a lattice. It is shown that for an ideal $I$ of a lattice $L$, $\sqrt{I}$ is a prime ideal of a lattice $L$ if and only if $\sqrt{I}$ is a primary ideal of $L$. Similarly, it is shown that for an ideal $I$ of a lattice $L$, $\sqrt{I}$ is a 2-absorbing ideal of a lattice $L$ if and only if $\sqrt{I}$ is a 2-absorbing primary ideal of $L$. We prove that $I_1\times L_2$ is a 2-absorbing primary ideal of $L=L_1\times L_2$ if and only if $I$ is a 2-absorbing primary ideal of $L_1$, where $I_1$ is a proper ideal of $L_1$.

The undefined terms are from Gratzer [9].

2 Preliminaries

We generalize the concepts of primary, 2-absorbing and 2-absorbing primary ideals from ring theory to lattices.

Definition 2.1

Let $I$ be an ideal of a lattice $L$. We define the radical of $I$ as the intersection of all prime ideals containing $I$ and we denote it as $\sqrt{I}$.

Remark 2.1

If there does not exist a prime ideal containing an ideal $I$ in a lattice $L$ then $\sqrt{I}=L$.

Remark 2.2

In a distributive lattice $L$, an ideal $I$ is the intersection of all prime ideals containing it see Gratzer [9, p. 75] i.e. $I=\sqrt{I}$.

However, this may or may not hold in a non distributive lattice.

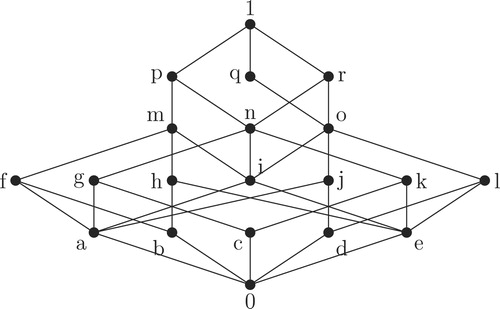
Example 2.1

Consider the ideal $I=\left(n\right]$ of the lattice shown in Fig. 1. The lattice is non distributive. We observe that $I=\sqrt{I}$ since $\sqrt{I}=\left(p\right]\cap \left(r\right]=\left(n\right]$.

short-legendFig. 1

The following example shows that $I\subset \sqrt{I}$.

Example 2.2

Consider the ideal $I=\left(l\right]$ of the lattice shown in Fig. 1. We observe that $I\subset \sqrt{I}$ since $\sqrt{I}=\left(q\right]\cap \left(r\right]=\left(o\right]$.

Definition 2.2

Let $L$ be a lattice. A proper ideal $I$ of $L$ is called primary if $a,b\in L$ and $a\wedge b\in I$ imply that either $a\in I$ or $b\in \sqrt{I}$.

Example 2.3

In the lattice $L$ shown in Fig. 1, consider the ideal $I=\left(m\right]$. Then $\sqrt{I}=\left(p\right]$. The ideal $I$ is a primary ideal.

Consider the ideal $I=\left(j\right]$ of a lattice shown in Fig. 1. Then $\sqrt{I}=\left(q\right]\cap \left(r\right]=\left(o\right]$. The ideal $I$ is not a primary ideal since $f\wedge g=a\in I$ but neither $f\in I$ nor $g\in I$. Also, neither $f\in \sqrt{I}$ nor $g\in \sqrt{I}$.

Definition 2.3

Let $L$ be a lattice. A proper ideal $I$ of $L$ is called 2-absorbing if for $a,b,c\in L$, $a\wedge b\wedge c\in I$ then either $a\wedge b\in I$ or $a\wedge c\in I$ or $b\wedge c\in I$.

Example 2.4

Consider the lattice $L$ shown in Fig. 1. Here the ideal $\left(n\right]$ is a 2-absorbing ideal.

Consider the ideal $I=\left(b\right]$ of a lattice shown in Fig. 1. The ideal $I$ is not a 2-absorbing ideal since $i\wedge j\wedge l=0\in I$ but neither $i\wedge j=a\in I$ nor $i\wedge l=e\in I$ nor $j\wedge l=d\in I$.

Definition 2.4

Let $L$ be a lattice. A proper ideal $I$ of $L$ is called a 2-absorbing primary if for $a,b,c\in L$, $a\wedge b\wedge c\in I$ then either $a\wedge b\in I$ or $a\wedge c\in \sqrt{I}$ or $b\wedge c\in \sqrt{I}$.

Example 2.5

In the lattice shown in Fig. 1, the ideal $\left(f\right]$ is a 2-absorbing primary.

Consider the lattice of divisors of $30$. Let $I=\left(0\right]$. Then $\sqrt{I}=\left(6\right]\cap \left(10\right]\cap \left(15\right]=\left(0\right]$. However, $6\wedge 10\wedge 15=0\in I$, but neither $6\wedge 10=2\in I$ nor $6\wedge 15=3\in I$ nor $10\wedge 15=5\in I$. Hence $I$ is not a 2-absorbing primary ideal.

3 Some properties of 2-absorbing primary ideals

The proofs of Lemma 3.1^{Lemma 3.2}–3.3 are obvious.

Lemma 3.1

If $I$ is a prime ideal of a lattice $L$, then $I$ is a primary ideal of $L$.

Remark 3.1

The following example shows that the converse of Lemma 3.1 does not hold.

Example 3.1

Consider the lattice $L$ shown in Fig. 1. For the ideal $I=\left(m\right]$, $\sqrt{I}=\left(p\right]$ as $\left(p\right]$ is the only prime ideal of $L$ containing $I$. $I$ is a primary ideal. However $k\wedge l=e\in I$ but neither $k\in I$ nor $l\in I$. Thus $I$ is not a prime ideal.

Lemma 3.2

If $I$ is a primary ideal of a lattice $L$, then $I$ is a 2-absorbing primary ideal of $L$.

Remark 3.2

The following example shows that the converse of Lemma 3.2 does not hold.

Example 3.2

Consider the ideal $I=\left(l\right]$ of the lattice shown in Fig. 1. Thus $\sqrt{I}=\left(q\right]\cap \left(r\right]=\left(o\right]$. Here $I$ is a 2-absorbing primary ideal. We note that $g\wedge h=0\in I$. However, neither $g\in I$ nor $h\in I$. Also, neither $g\in \sqrt{I}$ nor $h\in \sqrt{I}$. Hence $I$ is not a primary ideal of $L$.

Lemma 3.3

If $I$ is a 2-absorbing ideal of a lattice $L$, then $I$ is a 2-absorbing primary ideal of $L$.

Remark 3.3

The following example shows that the converse of Lemma 3.3 does not hold.

Example 3.3

Consider the ideal $I=\left(0\right]$ of the lattice shown in Fig. 1. Thus $\sqrt{I}=\left(p\right]\cap \left(q\right]\cap \left(r\right]=\left(i\right]$. Here $I$ is a 2-absorbing primary ideal. However $i\wedge j\wedge l=0\in I$, but neither $i\wedge j=a\in I$ nor $i\wedge l=e\in I$ nor $j\wedge l=d\in I$. Hence $I$ is not a 2-absorbing ideal of $L$.

The following lemma is from Wasadikar and Gaikwad [8].

Lemma 3.4

Let $P_1$ and $P_2$ be two distinct prime ideals of a lattice $L$, then $P_1\cap P_2$ is a 2-absorbing ideal of $L$.

Definition 3.1

Let $I$ be an ideal of a lattice $L$. We define $I$ as a $P$-primary ideal of $L$ if $P$ is the only prime ideal containing $I$.

Example 3.4

In the lattice shown in Fig. 1, the ideal $\left(m\right]$ is a $P$-primary ideal, where $P=\left(p\right]$ is the only prime ideal containing $\left(m\right]$.

The following result is an analog of [3, Theorem 2.4 (2)].

Theorem 3.1

Let $L$ be a lattice. Suppose that $I_1$ is a $P_1$-primary ideal of $L$ for some prime ideal $P_1$ of $L$ and $I_2$ is a $P_2$-primary ideal of $L$ for some prime ideal $P_2$ of $L$. Then $I_1\cap I_2$ is a 2-absorbing primary ideal of $L$.

Proof

Let $I=I_1\cap I_2$. Then $\sqrt{I}=P_1\cap P_2$. Now suppose that $x\wedge y\wedge z\in I$ for some $x,y,z\in L$, $x\wedge z\notin \sqrt{I}$ and $y\wedge z\notin \sqrt{I}$. Then $x,y,z\notin \sqrt{I}=P_1\cap P_2$. By Lemma 3.4, $\sqrt{I}=P_1\cap P_2$ is a 2-absorbing ideal of $L$. Since $x\wedge z,y\wedge z\notin \sqrt{I}$, we have $x\wedge y\in \sqrt{I}$.

We show that $x\wedge y\in I$. Since $x\wedge y\in \sqrt{I}\subseteq P_1$, we may assume that $x\in P_1$. As $x\notin \sqrt{I}$ and $x\wedge y\in \sqrt{I}\subseteq P_2$, we conclude that $x\notin P_2$ and $y\in P_2$. Since $y\in P_2$ and $y\notin \sqrt{I}$, we have $y\notin P_1$.

If $x\in I_1$ and $y\in I_2$, then $x\wedge y\in I$ and we are done. We may assume that $x\notin I_1$. Since $I_1$ is a $P_1$-primary ideal and $x\notin I_1$, we have $y\wedge z\in P_1$. Since $y\in P_2$ and $y\wedge z\in P_1$, we have $y\wedge z\in \sqrt{I}$, which is a contradiction. Thus $x\in I_1$.

Since $I_2$ is a $P_2$-primary ideal of $L$ and if $y\notin I_2$ then $x\wedge z\in P_2$. Since $x\in P_1$ and $x\wedge z\in P_1$, we have $x\wedge z\in \sqrt{I}$, which is a contradiction. Thus $y\in I_2$. Hence $x\wedge y\in I$. □

Theorem 3.2

Let $I$ be a proper ideal of a lattice $L$ such that $\sqrt{I}$ is a prime ideal of $L$. Then $I$ is a 2-absorbing primary ideal of $L$.

Proof

Suppose that $a\wedge b\wedge c\in I$ for some $a,b,c\in L$ and $a\wedge b\notin I$.

$\left(a\right)$ Suppose that $a\wedge b\notin \sqrt{I}$. Since $\sqrt{I}$ is a prime ideal of $L$, $c\in \sqrt{I}$ and so $a\wedge c\in \sqrt{I}$ and $b\wedge c\in \sqrt{I}$.

$\left(b\right)$ Suppose that $a\wedge b\in \sqrt{I}$. As $\sqrt{I}$ is a prime ideal, we have either $a\in \sqrt{I}$ or $b\in \sqrt{I}$. Hence $a\wedge c\in \sqrt{I}$ or $b\wedge c\in \sqrt{I}$. Thus $I$ is a 2-absorbing primary ideal of $L$. □

Remark 3.4

However, the converse of Theorem 3.2 need not hold.

Example 3.5

Consider the ideal $I=\left(l\right]$ of the lattice shown in Fig. 1. Thus $\sqrt{I}=\left(q\right]\cap \left(r\right]=\left(o\right]$. Here $I$ is a 2-absorbing primary ideal. However, $g\wedge h=0\in \sqrt{I}$, but neither $g\in \sqrt{I}$ nor $h\in \sqrt{I}$. Thus $\sqrt{I}$ is not a prime ideal of $L$.

Theorem 3.3

Let $I$ be an ideal of a lattice $L$. Then $\sqrt{I}$ is a prime ideal of $L$ if and only if $\sqrt{I}$ is a primary ideal of $L$.

Proof

Suppose that $\sqrt{I}$ is a prime ideal of $L$. If $a\wedge b\in \sqrt{I}$ then either $a\in \sqrt{I}$ or $b\in \sqrt{I}$. As $\sqrt{I}=\sqrt{\sqrt{I}}$, either $a\in \sqrt{I}$ or $b\in \sqrt{\sqrt{I}}$. Hence $\sqrt{I}$ is a primary ideal of $L$.

Conversely, suppose that $\sqrt{I}$ is a primary ideal of $L$. Let $a\wedge b\in \sqrt{I}$. As $\sqrt{I}$ is a primary ideal, either $a\in \sqrt{I}$ or $b\in \sqrt{\sqrt{I}}=\sqrt{I}$. Thus $\sqrt{I}$ is a prime ideal of $L$. □

Similarly, we can prove the following characterization for 2-absorbing and 2-absorbing primary ideals of a lattice $L$.

Theorem 3.4

Let $I$ be an ideal of a lattice $L$. Then $\sqrt{I}$ is a 2-absorbing ideal of $L$ if and only if $\sqrt{I}$ is a 2-absorbing primary ideal of $L$.

Theorem 3.5

Let $I$ be a 2-absorbing primary ideal of a lattice $L$ and suppose that $x\wedge y\wedge J\subseteq I$ for some $x,y\in L$ and some ideal $J$ of $L$. If $x\wedge y\notin I$, then $x\wedge J\subseteq \sqrt{I}$ or $y\wedge J\subseteq \sqrt{I}$.

Proof

Let $x\wedge y\notin I$. Suppose that $x\wedge J⊈\sqrt{I}$ and $y\wedge J⊈\sqrt{I}$. Then there exist some $j_1$ and some $j_2$ in $J$ such that $x\wedge j_1\notin \sqrt{I}$ and $y\wedge j_2\notin \sqrt{I}$. As $x\wedge y\wedge j_1\in I$, we have $y\wedge j_1\in \sqrt{I}$ since $I$ is a 2-absorbing primary ideal. Similarly, $x\wedge y\wedge j_2\in I$ implies $x\wedge j_2\in \sqrt{I}$.

Since $x\wedge y\wedge (j_1\vee j_2)\in I$ and $x\wedge y\notin I$, we have either $x\wedge (j_1\vee j_2)\in \sqrt{I}$ or $y\wedge (j_1\vee j_2)\in \sqrt{I}$. Suppose that $x\wedge (j_1\vee j_2)\in \sqrt{I}$. Therefore, $(x\wedge j_1)\vee (x\wedge j_2)\le x\wedge (j_1\vee j_2)\in \sqrt{I}$ and so $(x\wedge j_1)\vee (x\wedge j_2)\in \sqrt{I}$. Hence $x\wedge j_2\in \sqrt{I}$ and $x\wedge j_1\in \sqrt{I}$, which is a contradiction.

Similarly, if $y\wedge (j_1\vee j_2)\in \sqrt{I}$ then $(y\wedge j_1)\vee (y\wedge j_2)\in \sqrt{I}$. Hence $y\wedge j_1\in \sqrt{I}$ and $y\wedge j_2\in \sqrt{I}$, which is a contradiction. Hence $x\wedge J\subseteq \sqrt{I}$ or $y\wedge J\subseteq \sqrt{I}$. □

Remark 3.5

The converse of Theorem 3.5 does not hold.

Example 3.6

Consider the ideal $I=\left(l\right]$ of the lattice shown in Fig. 1. Thus $\sqrt{I}=\left(o\right]$. $I$ is a 2-absorbing primary ideal. Consider the ideal $J=\left(e\right]$. Now, $h\wedge i\wedge J=J\subseteq I$, $h\wedge J=J\subseteq I$ and $i\wedge J=J\subseteq I$, but $h\wedge i\in I$.

We give a characterization of a 2-absorbing primary ideal, which is an analog of [3, Theorem 2.19].

Theorem 3.6

Let $I$ be a proper ideal of a lattice $L$. Then $I$ is a 2-absorbing primary ideal if and only if whenever $I_1{I}_2{I}_3\subseteq I$ for some ideals $I_1,I_2,I_3$ of $L$, then $I_1{I}_2\subseteq I$ or $I_1{I}_3\subseteq \sqrt{I}$ or $I_2{I}_3\subseteq \sqrt{I}$.

Proof

Let $I$ be an ideal of $L$ such that if $I_1{I}_2{I}_3\subseteq I$ for some ideals $I_1,I_2,I_3$ of $L$ then $I_1{I}_2\subseteq I$ or $I_1{I}_3\subseteq I$ or $I_2{I}_3\subseteq I$ or $I_1{I}_3\subseteq \sqrt{I}$ or $I_2{I}_3\subseteq \sqrt{I}$. We show that $I$ is a 2-absorbing primary ideal of $L$. Let $a\wedge b\wedge c\in I$ for $a,b,c\in L$. This implies that $\left(a\right]\wedge \left(b\right]\wedge \left(c\right]\subseteq I$. Let $I_1=\left(a\right]$, $I_2=\left(b\right]$ and $I_3=\left(c\right]$. By hypothesis, either $I_1{I}_2\subseteq I$ or $I_1{I}_3\subseteq \sqrt{I}$ or $I_2{I}_3\subseteq \sqrt{I}$. Hence either $a\wedge b\in I$ or $a\wedge c\in \sqrt{I}$ or $b\wedge c\in \sqrt{I}$. Thus $I$ is a 2-absorbing primary ideal of $L$.

Conversely, suppose that $I$ is a 2-absorbing primary ideal. Let $I_1{I}_2{I}_3\subseteq I$ for some ideals $I_1,I_2,I_3$ of $L$. Suppose that $I_1{I}_2⊈I$. We show that $I_1{I}_3\subseteq \sqrt{I}$ or $I_2{I}_3\subseteq \sqrt{I}$. Suppose that $I_1{I}_3⊈\sqrt{I}$ and $I_2{I}_3⊈\sqrt{I}$. Then there exist $q_1\in I_1$ and $q_2\in I_2$ such that $q_1\wedge I_3⊈\sqrt{I}$ and $q_2\wedge I_3⊈\sqrt{I}$. As $q_1\wedge q_2\wedge I_3\subseteq I$, we have $q_1\wedge q_2\in I$ by Theorem 3.5. Since $I_1{I}_2⊈I$, we have $a\wedge b\notin I$ for some $a\in I_1$, $b\in I_2$. Since $a\wedge b\wedge I_3\subseteq I$ and $a\wedge b\notin I$, we have $a\wedge I_3\subseteq \sqrt{I}$ or $b\wedge I_3\subseteq \sqrt{I}$ by Theorem 3.5. We consider three cases.

Case 1: Suppose that $a\wedge I_3\subseteq \sqrt{I}$ but $b\wedge I_3⊈\sqrt{I}$. Since $q_1\wedge b\wedge I_3\subseteq I$ and $b\wedge I_3⊈\sqrt{I}$ and $q_1\wedge I_3⊈\sqrt{I}$, we conclude that $q_1\wedge b\in I$ by Theorem 3.5. Since $(a\vee q_1)\wedge b\wedge I_3\subseteq I$ and $a\wedge I_3\subseteq \sqrt{I}$, but $q_1\wedge I_3⊈\sqrt{I}$, we conclude that $(a\vee q_1)\wedge I_3⊈\sqrt{I}$. Since $b\wedge I_3⊈\sqrt{I}$ and $(a\vee q_1)\wedge I_3⊈\sqrt{I}$, we conclude that $(a\vee q_1)\wedge b\in I$ by Theorem 3.5. Since $(a\wedge b)\vee (q_1\wedge b)\le (a\vee q_1)\wedge b\in I$, we have $(a\wedge b)\vee (q_1\wedge b)\in I$. Thus $q_1\wedge b\in I$ and $a\wedge b\in I$, a contradiction.

Case 2: Suppose that $b\wedge I_3\subseteq \sqrt{I}$, but $a\wedge I_3⊈\sqrt{I}$.

Since $a\wedge q_2\wedge I_3\subseteq I$ and $a\wedge I_3⊈\sqrt{I}$ and $q_2\wedge I_3⊈\sqrt{I}$, we conclude that $a\wedge q_2\in I$ by Theorem 3.5. Since $a\wedge (b\vee q_2)\wedge I_3\subseteq I$ and $b\wedge I_3\subseteq \sqrt{I}$, but $q_2\wedge I_3⊈\sqrt{I}$, we conclude that $(b\vee q_2)\wedge I_3⊈\sqrt{I}$. Since $a\wedge I_3⊈\sqrt{I}$ and $(b\vee q_2)\wedge I_3⊈\sqrt{I}$, we conclude that $a\wedge (b\vee q_2)\in I$ by Theorem 3.5. Since $(a\wedge b)\vee (a\wedge q_2)\le a\wedge (b\vee q_2)\in I$, we have $(a\wedge b)\vee (a\wedge q_2)\in I$. Thus $a\wedge q_2\in I$ and $a\wedge b\in I$, a contradiction.

Case 3: $a\wedge I_3\subseteq \sqrt{I}$ and $b\wedge I_3\subseteq \sqrt{I}$.

Since $b\wedge I_3\subseteq \sqrt{I}$ and $q_2\wedge I_3⊈\sqrt{I}$, we conclude that $(b\vee q_2)\wedge I_3⊈\sqrt{I}$. Since $q_1\wedge (b\vee q_2)\wedge I_3\subseteq I$ and $q_1\wedge I_3⊈\sqrt{I}$ and $(b\vee q_2)\wedge I_3⊈\sqrt{I}$, we conclude that $q_1\wedge (b\vee q_2)\in I$ by Theorem 3.5. As $(q_1\wedge b)\vee (q_1\wedge q_2)\le q_1\wedge (b\vee q_2)\in I$, we have $(q_1\wedge b)\vee (q_1\wedge q_2)\in I$. Hence $b\wedge q_1\in I$. Since $a\wedge I_3\subseteq \sqrt{I}$ and $q_1\wedge I_3⊈\sqrt{I}$, we conclude that $(a\vee q_1)\wedge I_3⊈\sqrt{I}$. Since $(a\vee q_1)\wedge q_2\wedge I_3\subseteq I$ and $q_2\wedge I_3⊈\sqrt{I}$ and $(a\vee q_1)\wedge I_3⊈\sqrt{I}$, we conclude that $(a\vee q_1)\wedge q_2\in I$ by Theorem 3.5. As $(a\wedge q_2)\vee (q_1\wedge q_2)\le (a\vee q_1)\wedge q_2\in I$, we have $(a\wedge q_2)\vee (q_1\wedge q_2)\in I$. Hence $a\wedge q_2\in I$. Now, since $(a\vee q_1)\wedge (b\vee q_2)\wedge I_3\subseteq I$ and $(a\vee q_1)\wedge I_3⊈\sqrt{I}$ and $(b\vee q_2)\wedge I_3⊈\sqrt{I}$, we conclude that $(a\vee q_1)\wedge (b\vee q_2)\in I$ by Theorem 3.5. We conclude that $a\wedge b\in I$, a contradiction. Hence $I_1{I}_3\subseteq \sqrt{I}$ or $I_2{I}_3\subseteq \sqrt{I}$. □

Theorem 3.7

Let $f:L\to L^{\prime }$ be a homomorphism of lattices. Then the following statements hold:

(1)	If $P^{\prime }$ is a prime ideal of $L^{\prime }$, then $f^{-1}\left(P^{\prime }\right)$ is a prime ideal of $L$.

(2)	If $f$ is an isomorphism and $P$ is a prime ideal of $L$, then $f\left(P\right)$ is a prime ideal of $L^{\prime }$.

Proof

(1) Let $a\wedge b\in f^{-1}\left(P^{\prime }\right)$ for $a,b\in L$. Then $f(a\wedge b)\in P^{\prime }$. Hence $f\left(a\right)\wedge f\left(b\right)\in P^{\prime }$. This implies that either $f\left(a\right)\in P^{\prime }$ or $f\left(b\right)\in P^{\prime }$. That is either $a\in f^{-1}\left(P^{\prime }\right)$ or $b\in f^{-1}\left(P^{\prime }\right)$. Thus $f^{-1}\left(P^{\prime }\right)$ is a prime ideal of $L$.

(2) Let $a^{\prime }\wedge b^{\prime }\in f\left(P\right)$ for $a^{\prime },b^{\prime }\in L^{\prime }$. Then there exist some $a,b\in L$ such that $f\left(a\right)=a^{\prime }$ and $f\left(b\right)=b^{\prime }$. Thus $f\left(a\right)\wedge f\left(b\right)=a^{\prime }\wedge b^{\prime }\in f\left(P\right)$. Thus $f(a\wedge b)\in f\left(P\right)$. Hence $a\wedge b\in P$. As $P$ is a prime ideal of L, either $a\in P$ or $b\in P$. That is either $f^{-1}\left(a^{\prime }\right)\in P$ or $f^{-1}\left(b^{\prime }\right)\in P$. Hence either $a^{\prime }\in f\left(P\right)$ or $b\in f\left(P\right)$. Thus $f\left(P\right)$ is a prime ideal of $L^{\prime }$. □

Theorem 3.8

Let $f:L\to L^{\prime }$ be a homomorphism of lattices. Then the following statements hold:

(1)	If $I^{\prime }$ is an ideal of $L^{\prime }$, then $f^{-1}\left(\sqrt{I^{\prime }}\right)=\sqrt{f^{-1}\left(I^{\prime }\right)}$.

(2)	If $f$ is an isomorphism and $I$ is an ideal of $L$, then $f\left(\sqrt{I}\right)=\sqrt{f\left(I\right)}$.

Proof

(1) Let $P_i^{\prime }$’s be all prime ideals of $L^{\prime }$ containing $I^{\prime }$ where $i\in \Lambda$. Then $f^{-1}\left(\sqrt{I^{\prime }}\right)=f^{-1}(\bigcap P_i^{\prime })$. Which implies that $f^{-1}\left(\sqrt{I^{\prime }}\right)=\bigcap f^{-1}\left(P_i^{\prime }\right)$. As $P_i^{\prime }$’s are prime ideals of $L^{\prime }$, $f^{-1}\left(P_i^{\prime }\right)$’s are prime ideals of $L$, by Theorem 3.7 (1) and as $I^{\prime }\subseteq \bigcap P_i^{\prime }$, we have $f^{-1}\left(I^{\prime }\right)\subseteq \bigcap f^{-1}\left(P_i^{\prime }\right)$. Which implies that $\bigcap f^{-1}\left(P_i^{\prime }\right)=\sqrt{f^{-1}\left(I^{\prime }\right)}$. Hence $f^{-1}\left(\sqrt{I^{\prime }}\right)=\sqrt{f^{-1}\left(I^{\prime }\right)}$.

(2) Let $P_i$’s be all prime ideals of $L$ containing $I$ where $i\in \Lambda$. Then $f\left(\sqrt{I}\right)=f(\bigcap P_i)$. This implies that $f\left(\sqrt{I}\right)=\bigcap f\left(P_i\right)$. As $P_i$’s are prime ideals of $L$, $f\left(P_i\right)$’s are prime ideals of $L^{\prime }$, by Theorem 3.7 (2) and as $I\subseteq \bigcap P_i$, we have $f\left(I\right)\subseteq \bigcap f\left(P_i\right)$. Implies that $\bigcap f\left(P_i\right)=\sqrt{f\left(I\right)}$. Hence $f\left(\sqrt{I}\right)=\sqrt{f\left(I\right)}$. □

The following result is an analog of [3, Theorem 2.20].

Theorem 3.9

Let $f:L\to L^{\prime }$ be a homomorphism of lattices. Then the following statements hold:

(1)	If $I^{\prime }$ is a 2-absorbing primary ideal of $L^{\prime }$, then $f^{-1}\left(I^{\prime }\right)$ is a 2-absorbing primary ideal of $L$.

(2)	If $f$ is an isomorphism and $I$ is a 2-absorbing primary ideal of $L$, then $f\left(I\right)$ is a 2-absorbing primary ideal of $L^{\prime }$.

Proof

$\left(1\right)$ Let $a,b,c\in L$ such that $a\wedge b\wedge c\in f^{-1}\left(I^{\prime }\right)$. Then $f(a\wedge b\wedge c)=f\left(a\right)\wedge f\left(b\right)\wedge f\left(c\right)\in I^{\prime }$. As $I^{\prime }$ is 2-absorbing primary ideal, we have either $f\left(a\right)\wedge f\left(b\right)\in I^{\prime }$ or $f\left(a\right)\wedge f\left(c\right)\in \sqrt{I^{\prime }}$ or $f\left(b\right)\wedge f\left(c\right)\in \sqrt{I^{\prime }}$. That is either $a\wedge b\in f^{-1}\left(I^{\prime }\right)$ or $a\wedge c\in f^{-1}\left(\sqrt{I^{\prime }}\right)$ or $b\wedge c\in f^{-1}\left(\sqrt{I^{\prime }}\right)$. As $f^{-1}\left(\sqrt{I^{\prime }}\right)=\sqrt{f^{-1}\left(I^{\prime }\right)}$, by Theorem 3.8 (1), $a\wedge b\in f^{-1}\left(I^{\prime }\right)$ or $a\wedge c\in \sqrt{f^{-1}\left(I^{\prime }\right)}$ or $b\wedge c\in \sqrt{f^{-1}\left(I^{\prime }\right)}$. Thus $f^{-1}\left(I^{\prime }\right)$ is a 2-absorbing primary ideal of $L$.

$\left(2\right)$ Let $a^{\prime },b^{\prime },c^{\prime }\in L^{\prime }$ and $a^{\prime }\wedge b^{\prime }\wedge c^{\prime }\in f\left(I\right)$. Then there exist $a,b,c\in L$ such that $f\left(a\right)=a^{\prime }$, $f\left(b\right)=b^{\prime }$, $f\left(c\right)=c^{\prime }$ and $f\left(a\right)\wedge f\left(b\right)\wedge f\left(c\right)=a^{\prime }\wedge b^{\prime }\wedge c^{\prime }\in f\left(I\right)$. That is $f\left(a\right)\wedge f\left(b\right)\wedge f\left(c\right)\in f\left(I\right)$. Hence $a\wedge b\wedge c\in I$. As $I$ is a 2-absorbing primary ideal, we have either $a\wedge b\in I$ or $a\wedge c\in \sqrt{I}$ or $b\wedge c\in \sqrt{I}$. That is either $f^{-1}(a^{\prime }\wedge b^{\prime })\in I$ or $f^{-1}(a^{\prime }\wedge c^{\prime })\in \sqrt{I}$ or $f^{-1}(b^{\prime }\wedge c^{\prime })\in I$. Thus either $a^{\prime }\wedge b^{\prime }\in f\left(I\right)$ or $a^{\prime }\wedge c^{\prime }\in f\left(\sqrt{I}\right)$ or $b^{\prime }\wedge c^{\prime }\in f\left(\sqrt{I}\right)$. As $f\left(\sqrt{I}\right)=\sqrt{f\left(I\right)}$, by Theorem 3.8 (2) $a^{\prime }\wedge b^{\prime }\in f\left(I\right)$ or $a^{\prime }\wedge c^{\prime }\in \sqrt{f\left(I\right)}$ or $b^{\prime }\wedge c^{\prime }\in \sqrt{f\left(I\right)}$. Hence $f\left(I\right)$ is a 2-absorbing ideal of $L^{\prime }$. □

4 2-absorbing primary ideals in product lattices

In this section we prove some results on 2-absorbing primary ideals in product lattices. The notion of the product lattice is from Gratzer [9, p. 27].

The proof of the following theorem is obvious.

Theorem 4.1

Let $L=L_1\times L_2$, where $L_1$ and $L_2$ are lattices. Let $P_i$’s and $Q_j$’s be ideals of $L_1$ and $L_2$ respectively, where $i\in {\Lambda }_1$ and $j\in {\Lambda }_2$. Then $\bigcap (P_i\times Q_j)=\bigcap P_i\times \bigcap Q_j$.

Theorem 4.2

Let $L=L_1\times L_2$, where each $L_i$, $(i=1,2)$ is a lattice with 1. Then the following hold:

(1)	If $I_1$ is an ideal of $L_1$, then $\sqrt{I_1\times L_2}=\sqrt{I_1}\times L_2$.

(2)	If $I_2$ is an ideal of $L_2$, then $\sqrt{L_1\times I_2}=L_1\times \sqrt{I_2}$.

Proof

(1) Let $(a,b)\in \sqrt{I_1\times L_2}$. Thus $(a,b)\in {\bigcap }_{i\in \Lambda }(P_i\times L_2)$, where and $P_i$’s are all prime ideals of a lattice $L_1$ containing $I_1$. Thus $a\in {\bigcap }_{i\in \Lambda }{P}_i$, $b\in L_2$. Thus $a\in \sqrt{I_1}$, $b\in L_2$ and so $(a,b)\in \sqrt{I_1}\times L_2$.

If $(a,b)\in \sqrt{I_1}\times L_2$ then $a\in \sqrt{I_1}$, $b\in L_2$. Thus $a\in {\bigcap }_{i\in \Lambda }{P}_i$, $b\in L_2$ and so $(a,b)\in {\bigcap }_{i\in \Lambda }(P_i\times L_2)$. i.e. $(a,b)\in \sqrt{I_1\times L_2}$. Hence $\sqrt{I_1\times L_2}=\sqrt{I_1}\times L_2$.

(2) Proof is similar to that of (1). □

The following characterization gives a relation between a 2-absorbing primary ideal of a product of two lattices and a 2-absorbing primary ideal of one of the lattice in this product.

Theorem 4.3

Let $L=L_1\times L_2$, where $L_1$ and $L_2$ are lattices. Let $I$ be a proper ideal of $L_1$. Then $I\times L_2$ is a 2-absorbing primary ideal if and only if $I$ is a 2-absorbing primary ideal of $L_1$.

Proof

Suppose that $I\times L_2$ is a 2-absorbing ideal of $L$. Let $a\wedge b\wedge c\in I$ for $a,b,c\in L_1$. Then $(a\wedge b\wedge c,x)\in I\times L_2$ for $x\in L_2$. As $I\times L_2$ is a 2-absorbing primary ideal of $L$, either $(a\wedge b,x)\in I\times L_2$ or $(a\wedge c,x)\in \sqrt{I\times L_2}$ or $(b\wedge c,x)\in \sqrt{I\times L_2}$. Then either $(a\wedge b,x)\in I\times L_2$ or $(a\wedge c,x)\in \sqrt{I}\times L_2$ or $(b\wedge c,x)\in \sqrt{I}\times L_2$, by Theorem 4.2. Hence either $a\wedge b\in I$ or $a\wedge c\in \sqrt{I}$ or $b\wedge c\in \sqrt{I}$.

Conversely, suppose that $I$ is a 2-absorbing primary ideal of $L_1$. Let $(a\wedge b\wedge c,x)\in I$ for $a,b,c\in L_1$ and $x\in L_2$. As $I$ is a 2-absorbing primary ideal of $L_1$, either $(a\wedge b,x)\in I\times L_2$ or $(a\wedge c,x)\in \sqrt{I}\times L_2$ or $(b\wedge c,x)\in \sqrt{I}\times L_2$. That is either $(a\wedge b,x)\in I\times L_2$ or $(a\wedge c,x)\in \sqrt{I\times L_2}$ or $(b\wedge c,x)\in \sqrt{I\times L_2}$, by Theorem 4.2. □

Theorem 4.4

Let $L=L_1\times L_2$, where $L_1$ and $L_2$ are lattices. Let $I_1$ and $I_2$ be proper ideals of $L_1$ and $L_2$ respectively. If $I=I_1\times I_2$ is a 2-absorbing primary ideal of $L$ then $I_1$ and $I_2$ are 2-absorbing primary ideals of $L_1$ and $L_2$ respectively.

Proof

Let $a\wedge b\wedge c\in I_1$ for some $a,b,c\in L_1$. Then $(a\wedge b\wedge c,x)\in I_1\times I_2$ for $x\in I_2$. As $I_1\times I_2$ is a 2-absorbing primary ideal, either $(a\wedge b,x)\in I_1\times I_2$ or $(a\wedge c,x)\in \sqrt{I_1\times I_2}$ or $(b\wedge c,x)\in \sqrt{I_1\times I_2}$, that is either $(a\wedge b,x)\in I_1\times I_2$ or $(a\wedge c,x)\in \sqrt{I_1}\times \sqrt{I_2}$ or $(b\wedge c,x)\in \sqrt{I_1}\times \sqrt{I_2}$, by Theorem 4.2. Hence $a\wedge b\in I_1$ or $a\wedge c\in \sqrt{I_1}$ or $b\wedge c\in \sqrt{I_1}$. Thus $I_1$ is a 2-absorbing primary ideal of $L_1$. Similarly, we can show that $I_2$ is a 2-absorbing primary ideal of $L_2$. □

Remark 4.1

The converse of Theorem 4.4 need not hold.

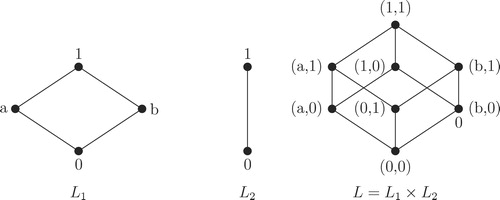
Example 4.1

Consider the lattices $L_1$, $L_2$ and $L=L_1\times L_2$ as shown in Fig. 2. Consider the ideals $I_1=0$, $I_2=0$ of the lattices $L_1$ and $L_2$ respectively. Thus $I_1\times I_2=(0,0)$ and $\sqrt{I_1\times I_2}=(0,0)$. The ideals $I_1$ and $I_2$ are 2-absorbing primary ideals of $L_1$ and $L_2$ respectively. But for $(a,1)\wedge (1,0)\wedge (b,1)=(0,0)\in I_1\times I_2$, neither $(a,1)\wedge (1,0)=(a,0)\in I_1\times I_2$ nor $(a,1)\wedge (b,1)=(0,1)\in I_1\times I_2$ nor $(1,0)\wedge (b,1)=(b,0)\in I_1\times I_2$. Thus $I_1\times I_2$ is not a 2-absorbing primary ideal of $L$.

short-legendFig. 2

Now we give a characterization of a 2-absorbing primary ideal in a product of two lattices, which is an analog of [3, Theorem 2.23].

Theorem 4.5

Let $L=L_1\times L_2$, where $L_1$ and $L_2$ are bounded lattices. Let $J$ be a proper ideal of $L$. Then the following statements are equivalent:

(1)	$J$ is a 2-absorbing primary ideal of $L$.

(2)	Either $J=I_1\times L_2$ for some 2-absorbing primary ideal $I_1$ of $L_1$ or $J=L_1\times I_2$ for some 2-absorbing primary ideal $I_2$ of $L_2$ or $J=I_1\times I_2$ for some primary ideal $I_1$ of $L_1$ and some primary ideal $I_2$ of $L_2$.

Proof

$\left(1\right)⟹\left(2\right)$. Suppose that $J$ is a 2-absorbing primary ideal of $L$. Then $J=I_1\times I_2$ for some ideal $I_1$ of $L_1$ and some ideal $I_2$ of $L_2$.

Case 1: If $I_2=L_2$ then $I_1\ne L_1$. Thus $J=I_1\times L_2$. Let $a\wedge b\wedge c\in I_1$ for some $a,b,c\in L_1$. Then $(a\wedge b\wedge c,x\wedge y\wedge z)\in I_1\times L_2$, where $x,y,z\in L_2$. As $J$ is a 2-absorbing primary ideal, we have either $(a\wedge b,x\wedge y)\in I_1\times L_2$ or $(a\wedge c,x\wedge z)\in \sqrt{I_1\times L_2}$ or $(b\wedge c,y\wedge z)\in \sqrt{I_1\times L_2}$. By Lemma 3.1, either $(a\wedge b,x\wedge y)\in I_1\times L_2$ or $(a\wedge c,x\wedge z)\in \sqrt{I_1}\times L_2$ or $(b\wedge c,y\wedge z)\in \sqrt{I_1}\times L_2$. Thus $I_1$ is a 2-absorbing primary ideal of $L_1$.

Case 2: If $I_1=L_1$ then $I_2\ne L_2$. Thus $J=L_1\times I_2$. Similarly, as in previous case, $I_2$ is a 2-absorbing primary ideal of $L_2$.

Case 3: Now if $I_1\ne L_1$ and $I_2\ne L_2$ then $J=I_1\times I_2$. That is $\sqrt{J}=\sqrt{I_1}\times \sqrt{I_2}$. On the contrary, suppose that $I_1$ is not a primary ideal of $L_1$. Then there are $a,b\in L_1$ such that $a\wedge b\in I_1$ but neither $a\in I_1$ nor $b\in \sqrt{I_1}$. Let $x=(a,1)$, $y=(1,0)$ and $c=(b,1)$. Then $x\wedge y\wedge c=(a\wedge b,0)\in J$ but neither $x\wedge y=(a,0)\in J$ nor $x\wedge c=(a\wedge b,1)\in \sqrt{J}$ nor $y\wedge c=(b,0)\in \sqrt{J}$, which is a contradiction. Thus $I_1$ is a primary ideal of $L_1$. Suppose that $I_2$ is not a primary ideal of $L_2$. Then there exist $d,e\in L_2$ such that $d\wedge e\in I_2$ but neither $d\in I_2$ nor $e\in \sqrt{I_2}$. Let $x=(1,d)$, $y=(0,1)$ and $c=(1,e)$. Then $x\wedge y\wedge c=(0,d\wedge e)\in J$ but neither $x\wedge y=(0,d)\in J$ nor $x\wedge c=(1,d\wedge e)\in \sqrt{J}$ nor $y\wedge c=(0,e)\in \sqrt{J}$, which is a contradiction. Thus $I_2$ is a primary ideal of $L_2$.

$\left(2\right)⟹\left(1\right)$. Suppose that $J=I_1\times L_2$ for some 2-absorbing primary ideal $I_1$ of $L_1$. Let $(a_1,b_1)\wedge (a_2,b_2)\wedge (a_3,b_3)\in I_1\times L_2$. Then $a_1\wedge a_2\wedge a_3\in I_1$. As $I_1$ is 2-absorbing primary ideal of $L_1$, we have either $a_1\wedge a_2\in I_1$ or $a_1\wedge a_3\in \sqrt{I_1}$ or $a_2\wedge a_3\in \sqrt{I_1}$. That is either $(a_1,b_1)\wedge (a_2,b_2)\in I_1\times L_2$ or $(a_1,b_1)\wedge (a_3,b_3)\in \sqrt{I_1}\times L_2$ or $(a_2,b_2)\wedge (a_3,b_3)\in \sqrt{I_1}\times L_2$. Hence either $(a_1,b_1)\wedge (a_2,b_2)\in I_1\times L_2$ or $(a_1,b_1)\wedge (a_3,b_3)\in \sqrt{I_1\times L_2}$ or $(a_2,b_2)\wedge (a_3,b_3)\in \sqrt{I_1\times L_2}$ by Theorem 4.2. Thus $J=I_1\times L_2$ is a 2-absorbing primary ideal of $L$. Similarly $L_1\times I_2$ is a 2-absorbing primary ideal of $L$. Suppose that $J=I_1\times I_2$ for some primary ideal $I_1$ of $L_1$ and some primary ideal $I_2$ of $L_2$. Then $P=I_1\times L_2$ and $Q=L_1\times I_2$ are primary ideals of $L$. Hence $P\cap Q=I_1\times I_2$. Thus $J=I_1\times I_2$ is a 2-absorbing primary ideal, by Theorem 3.1. □

The following theorem is a generalization of Theorem 4.5, which is an analog of [3, Theorem 2.24].

Theorem 4.6

Let $L=L_1\times L_2\cdots \times L_n$, where $2\le n<\infty$, and $L_1,L_2,\dots ,L_n$ are lattices. Let $J$ be a proper ideal of $L$. Then the following statements are equivalent.

(1)	$J$ is a 2-absorbing primary ideal of $L$.

(2)

Either $J={\prod }_{t=1}^n{I}_t$ such that for some $k\in 1,2,\dots ,n$, $I_k$ is a 2-absorbing primary ideal of $L_k$, and $I_t=L_t$ for every $t\in 1,2,\dots ,n\setminus k$ or $J={\prod }_{t=1}^n{I}_t$ such that for some $k,m\in 1,2,\dots ,n$, $I_k$ is a primary ideal of $L_k$, $I_m$ is a primary ideal of $L_m$, and $I_t\ne L_t$ for every $t\in 1,2,\dots ,n\setminus k,m$.

Proof

$\left(1\right)\iff \left(2\right)$ We prove this theorem by induction on $n$. Assume $n=2$. Then by Theorem 4.5, the result holds. Thus suppose that $3\le n<\infty$ and assume that the result is valid when $K=L_1\times L_2\cdots L_{n-1}$. Now we prove the result when $L=K\times L_n$. By Theorem 4.5, $J$ is a 2-absorbing primary ideal of $L$ if and only if either $J=A\times L_n$ for some 2-absorbing primary ideal $A$ of $K$ or $J=K\times A_n$ for some 2-absorbing primary ideal $A_n$ of $L_n$ or $J=A\times A_n$ for some primary ideal $A$ of $K$ and some primary ideal $A_n$ of $L_n$. Now observe that a proper ideal $B$ of $K$ is a primary ideal of $K$ if and only if $B={\prod }_{t=1}^{n-1}{I}_t$ such that for some $k\in 1,2,\dots ,n-1$, $I_k$ is a primary ideal of $L_k$, and $I_t\ne L_t$ for every $t\in 1,2,\dots ,n-1\setminus k,m$. □

Notes

Peer review under responsibility of Kalasalingam University.