Generalizations of supplemented lattices

Peer review under responsibility of Kalasalingam University.

Abstract

Some generalizations of the concept of a supplemented lattice, namely a soc-supplemented-lattice, soc-amply-supplemented-lattice, soc-weak-supplemented-lattice, soc-$\oplus$-supplemented-lattice and completely soc-$\oplus$-supplemented-lattice are introduced. Various results are proved to show the relationship between these lattices. We have also proved that, if $L$ is a soc-$\oplus$-supplemented-lattice satisfying the summand intersection property (SIP), then $L$ is a completely soc-$\oplus$-supplemented-lattice.

Keywords:

• Modular lattice
• Supplemented lattice
• Soc-supplemented-lattice
• Soc-amply-supplemented-lattice
• Soc-weak-supplemented-lattice

1 Introduction

Mutlu [1], Tohidi [2], Wang and Ding [3], Wisbauer [4] and many others have studied the concept of a supplemented module and its generalizations. Let $N$ and $L$ be submodules of a module $M$. $N$ is called a $supplement$ of $L$ if $N+L=M$ and $N$ is minimal with respect to this property. A module $M$ is called an $amply$ $supplemented$ $module$ if for any two submodules $A$ and $B$ of $M$ with $A+B=M$, $B$ contains a supplement of $A$. A module $M$ is called $\oplus \text{-}\mathit{supplemented}$ if each submodule of $M$ has a supplement that is a direct summand of $M$.

In 2012, Tohidi [2] introduced some generalizations of the concept of a supplemented module namely, a soc-supplemented-module, a soc-amply-supplemented-module, a soc-weak-supplemented-module, a soc-$\oplus$-supplemented-module and a completely soc-$\oplus$-supplemented-module. He proved various results to show relationship between these modules. He showed that, a direct summand of a soc-amply-supplemented-module is also a soc-amply-supplemented-module.

Călugăreanu [5] used lattice theory in module theory and studied several concepts from module theory in lattice theory. He introduced the concept of a supplement in terms of elements. Alizade and Toksoy [6] introduced the concepts of an ample supplement and an amply supplemented lattice in the context of a complete modular lattice. In [7] they also introduced the concepts of a weak supplement, a weakly supplemented lattice in the context of a complete modular lattice.

In this paper, we introduce the concepts of a soc-supplemented-lattice, a soc-amply-supplemented-lattice, a soc-weak-supplemented-lattice, a soc-$\oplus$-supplemented-lattice and a completely soc-$\oplus$-supplemented-lattice and obtain some results in the context of modular lattices.

Throughout in this paper $L$ denotes a lattice. Wherever necessary we assume that $Soc\left(a\right)$ exists for any $a\in L$ and $Soc\left(L\right)=Soc\left(1\right)$.

2 Preliminaries

We recall some terms from lattice theory. These and undefined terms can be found in Grätzer [8].

Definition 1

A lattice $L$ is called modular if for $a,b,c\in L$ with $a\le c$, $a\vee (b\wedge c)=(a\vee b)\wedge c$.

Definition 2

If $a,b,c\in L$ are such that $a\vee b=c$ and $a\wedge b=0$ then we say that $a,b$ are direct summands of $c$ and we write $c=a\oplus b$. We say that $c$ is a direct sum of $a$ and $b$.

Definition 3

Let $L$ be a lattice with 0. An element $a\in L$ is called an atom, if there does not exist any $b\in L$ such that $0<b<a$.

Definition 4

A lattice $L$ with 0 is said to be an atomistic lattice if every non-zero element $a\in L$ is the join of atoms of $L$ contained in $a$.

Definition 5

[5, p. 47]

The join of all atoms of $L$, denoted by $Soc\left(L\right)$, is called the socle of the lattice $L$.

For $a\in L$, $Soc\left(a\right)$ is the socle of the lattice $[0,a]$.

We recall some definitions from Alizade and Toksoy [6,7] and from Călugăreanu [5].

Definition 6

An element $a\in L$ is said to be small in $L$ if $a\vee b\ne 1$ for every $b\ne 1$. We then write $a\ll L$.

Definition 7

An element $a\in L$ is called a supplement of an element $b\in L$ if $a\vee b=1$ and $a$ is minimal with respect to this property.

Lemma 1

Let $L$ be a modular lattice and $a,b\in L$. $a$ is a supplement of $b$ in $L$ if and only if $a\vee b=1$ and $a\wedge b$ is small in $[0,a]$.

Proof

Suppose that $a$ is a supplement of $b$ in $L$. Then $a\vee b=1$ and $a$ is minimal with respect to this property. Let $(a\wedge b)\vee c=a$ for some $c\in [0,a],c<a$. Then $1=a\vee b=(a\wedge b)\vee c\vee b=b\vee c=1$, a contradiction. Hence $a\wedge b$ is small in $[0,a]$.

Conversely, suppose that $a\vee b=1$ and $a\wedge b$ is small in $[0,a]$. Let $c\vee b=1$ for some $c<a$. We have $c\vee (b\wedge a)=(c\vee b)\wedge a=a$, a contradiction. Hence $a$ is a supplement of $b$ in $L$.

Remark 1

The above equivalence does not hold in a nonmodular lattice.

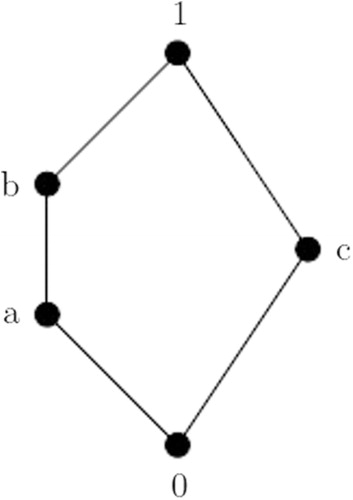
Example 1

In the lattice shown in Fig. 1, $b\vee c=1$ and $b\wedge c=0$ is small in $[0,b]$ but $b$ is not a supplement of $c$.

short-legendFig. 1

Definition 8

An element $a\in L$ is said to have ample supplements in $L$ if for every element $b\in L$ with $a\vee b=1$, $[0,b]$ contains a supplement of $a$ in $L$.

A lattice $L$ is said to be amply supplemented if every element $a\in L$ has ample supplements in $L$.

Definition 9

An element $a\in L$ is a weak supplement of $b\in L$ in $L$ if and only if $a\vee b=1$ and $a\wedge b\ll L$.

A lattice $L$ is said to be weakly supplemented if every element $a\in L$ has a weak supplement in $L$.

3 Soc-s-lattices, soc-a-s-lattices and soc-w-s-lattices

In this section, $L$ denotes a lattice with $0$ and $1$.

Definition 10

Let $a,b\in L$, $a\ne 0,1$ and $b\ne 0,1$ be such that $a\vee b=1$, then $b$ is called a soc-supplement of $a$ in case $a\wedge b\le Soc\left(b\right)$.

An element $a\in L$ is called a soc-supplement element if $a$ is a soc-supplement of some element in $L$.

A lattice $L$ is called a soc-supplemented lattice if every element of $L$ has a soc-supplement in $L$. In short we say that $L$ is a soc-s-lattice.

Example 2

Every complemented lattice is a soc-supplemented lattice.

Example 3

Let $L$ be a finite lattice with only one atom and two dual atoms whose meet is different from that atom. Then $L$ is not a soc-supplemented lattice.

Definition 11

A lattice $L$ is called a soc-amply-supplemented lattice if $1=a\vee b$, where $a,b\in L$ imply that $a$ has a soc-supplement $c\in L$ such that $c\le b$. In short we say that $L$ is a soc-a-s-lattice.

An element $a\in L$ is called a soc-amply-supplemented element if $a=b\vee c$, where $b\le a,c\le a$ imply that $b$ has a soc-supplement $d\le a$ such that $d\le c$. In short we say that $a$ is a soc-a-s-element.

Let $L$ be a lattice and $a\in L$. $a$ is said to have a soc-ample-supplement in $L$ if for any $b\in L$ with $a\vee b=1$, $a$ has a soc-supplement $c\in L$ such that $c\le b$.

Example 4

Every atomistic complemented lattice is a soc-a-s-lattice.

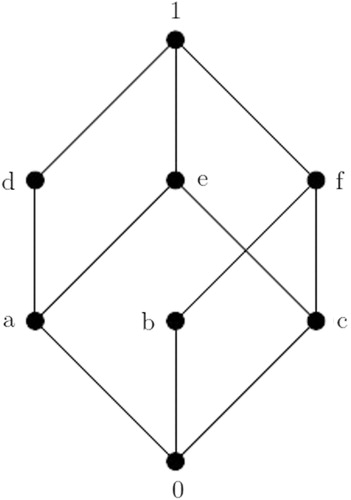
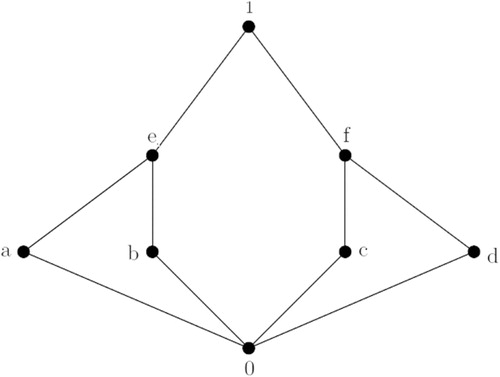
Example 5

In the lattice $L$ shown in Fig. 2, for elements $e,f\in L$, $1=e\vee f$, here $c\le f$ but $c$ is not a soc-supplement of $e$ because $c\vee e\ne 1$. Hence $L$ is not a soc-a-s-lattice.

short-legendFig. 2

The following two results are analogues of Proposition 2.1 and Lemma 2.2 from Tohidi [2].

Theorem 2

Let $L$ be a modular soc-a-s-lattice and $a\in L$ be a direct summand of $1$. Then $a$ is a soc-a-s-element.

Proof

Let $L$ be a soc-a-s-lattice and let $a$ be a direct summand of $1$. Then $a\oplus b=1$ for some $b\in L$.

To show: $a$ is a soc-a-s-element. Let $a=c\vee d$, where $c,d\in L$. Then $1=(c\vee d)\vee b=c\vee (d\vee b)=c\vee (d\oplus b)$. Since $L$ is a soc-a-s-lattice, there exists $f\in L$ such that $f\le c$ with $f\vee (d\oplus b)=1$ and $f\wedge (d\oplus b)\le Soc\left(f\right)$. Now, by using modularity, we get $a=a\wedge [f\vee (d\vee b)]=f\vee [(d\vee b)\wedge a]=f\vee [d\vee (b\wedge a)]=f\vee d.$Also, $f\wedge d\le f\wedge (d\oplus b)\le Soc\left(f\right)$. Hence $a$ is a soc-a-s-element.

Theorem 3

Let $L$ be a modular lattice, $a,b\in L$ and $a$ be a soc-s-element. If $a\vee b$ has a soc-supplement in $L$ then so does $b$.

Proof

Suppose that $a\vee b$ has a soc-supplement say $c$ in $L$. Then $(a\vee b)\vee c=1$ and $(a\vee b)\wedge c\le Soc\left(c\right)$. Since $a$ is a soc-s-element and $(c\vee b)\wedge a\le a$, there exists $d\in L$ such that $d\le a$, $a=[(c\vee b)\wedge a]\vee d$ and $[(c\vee b)\wedge a]\wedge d\le Soc\left(d\right)$. Then $(c\vee b)\wedge d\le Soc\left(d\right)$. Now, by modularity, we get $1=a\vee b\vee c=[(c\vee b)\wedge a]\vee d\vee b\vee c=a\wedge [(c\vee b)\vee d]\vee (b\vee c)=(b\vee c\vee a)\wedge (c\vee b\vee d)=(c\vee b)\vee d.$Thus, $d$ is a soc-supplement of $c\vee b$ in $L$.

Claim

$c\vee d$ is a soc-supplement of $b$ in $L$.

Clearly $(c\vee d)\vee b=1$. We have $(d\vee b)\wedge c\le (a\vee b)\wedge c\le Soc\left(c\right)$. By modularity, we get

$(c\vee d)\wedge b\le (c\vee d)\wedge (d\vee b)\wedge (c\vee b)\le (d\vee b)\wedge (c\vee d)\wedge (c\vee b)\le [(d\vee b)\wedge c]\vee d\wedge (c\vee b)\le [c\wedge (d\vee b)]\vee [d\wedge (c\vee b)]\le Soc\left(c\right)\vee Soc\left(d\right)\le Soc(c\vee d).$

Thus $c\vee d$ is a soc-supplement of $b$ in $L$.

Theorem 4

Let $L$ be a modular lattice and $a,b\in L$ be soc-supplemented elements. If $1=a\oplus b$, then $L$ is a soc-s-lattice.

Proof

Let $c\in L$ be such that $a\vee b\vee c=1$ and $a\vee b\vee c$ has trivially a soc-supplement 0 in $L$. Then by Theorem 3, $b\vee c$ has a soc-supplement in $L$. Again by Theorem 3, $c$ has a soc-supplement in $L$. Hence $L$ is a soc-s-lattice.

The following result is analogue of Proposition 2.5 from Tohidi [2].

Theorem 5

Let $L$ be a modular lattice and $a,b\in L$ be such that $a\vee b=1$. If $a$ and $b$ have soc-ample-supplements in $L$ then $a\wedge b$ also has a soc-ample-supplement in $L$.

Proof

Let $a,b\in L$ be such that $a\vee b=1$. Suppose that $a$ and $b$ have soc-ample-supplements in $L$.

To show: $a\wedge b$ has a soc-ample-supplement in $L$. Let $c\in L$ be such that $(a\wedge b)\vee c=1$. Then $a=(a\wedge b)\vee (c\wedge a)$ and $b=(a\wedge b)\vee (c\wedge b)$. Therefore, $1=a\vee (c\wedge b)$ and $1=b\vee (c\wedge a)$. Since $a$ and $b$ have soc-ample-supplements in $L$, there exist $d,e\in L$ such that $d\le c\wedge b$ and $e\le c\wedge a$. Also $a\vee d=1$, $a\wedge d\le Soc\left(d\right)$ and $b\vee e=1$, $b\wedge e\le Soc\left(e\right)$. Now $d\le c$ and $e\le c$ implies that $d\vee e\le c$. Now, $a=(a\wedge b)\vee e$ and $b=(b\wedge a)\vee d$. Therefore, $1=(a\wedge b)\vee (e\vee d)$. Now, by modularity, we get

$(e\vee d)\wedge (a\wedge b)\le (e\vee d)\wedge (d\vee (a\wedge b))\wedge (e\vee (a\wedge b))\le (d\vee (a\wedge b))\wedge (e\vee d)\wedge (e\vee (a\wedge b))\le d\vee [e\wedge (d\vee (a\wedge b))]\wedge (e\vee (a\wedge b))\le [e\wedge (d\vee (a\wedge b))]\vee [d\wedge (e\vee (a\wedge b))]\le [e\wedge (d\vee a)\wedge b]\vee [d\wedge (e\vee b)\wedge a]\le [e\wedge 1\wedge b]\vee [d\wedge 1\wedge a]\le (e\wedge b)\vee (d\wedge a)\le Soc\left(e\right)\vee Soc\left(d\right)\le Soc(e\vee d).$

Hence $d\vee e$ is a soc-a-supplement of $a\wedge b$ in $L$.

The following result is an analogue of Theorem 2.6 from Tohidi [2].

Theorem 6

Let $L$ be a modular lattice and $a\in L$. Then the following statements are equivalent.

(i) There is a decomposition $1=b\oplus c$, where $b,c\in L$ with $b\le a$ and $c\wedge a\le Soc\left(c\right)$.

(ii) $a$ has a soc-supplement $d\in L$ in $L$ such that $d\wedge a$ is a direct summand of $a$.

Proof

$\left(i\right)\Rightarrow \left(ii\right)$ Let $1=b\oplus d$ with $b\le a$ and $d\wedge a\le Soc\left(d\right)$. Then $a\vee d=1$ and $a\wedge d\le Soc\left(d\right)$ which means $d$ is a soc-supplement of $a$ in $L$.

We have $a=a\wedge 1=a\wedge (b\vee d)=b\vee (d\wedge a)$ by using modularity. Also $b\wedge (d\wedge a)=0$. Hence $d\wedge a$ is a direct summand of $a$.

$\left(ii\right)\Rightarrow \left(i\right)$ Suppose that $d$ is a soc-supplement of $a$ such that $a=b\oplus (d\wedge a)$. Then, $1=a\vee d=b\vee (d\wedge a)\vee d=b\vee d$ and $b\wedge d=(b\wedge a)\wedge d=0$. Hence $b$ is a direct summand of $1$.

Călugăreanu [5] developed the concept of an essential element in a lattice with least element 0.

Definition 12

[5, p. 39]

Let $L$ be a lattice with 0. An element $a\in L$ is called an essential element if $a\wedge b\ne 0$, for any nonzero $b\in L$.

If $a$ is essential in $[0,b]$ then we say that $a$ is essential in $b$ and write $a{\le }_{e}b$ and call $b$ as an essential extension of $a$.

If $a{\le }_{e}b$ and there is no $c\in L$ such that $a{\le }_{e}c$ and $b<c$, then we say that $b$ is a maximal essential extension of $a$.

Theorem 7

Let $L$ be a modular lattice, $a,b\in L$. Let $b$ be a soc-supplement of $a$ in $L$. If $a$ is an essential element of $L$, then $a\wedge b=Soc\left(b\right)$ is a minimal essential element of $[0,b]$.

Proof

Let $0\ne c\in L$ be such that $c\le b$. Since $a$ is essential in $L$, $a\wedge c\ne 0$, so $(a\wedge b)\wedge c\ne 0$. Thus $a\wedge b$ is an essential element in $[0,b]$. Now $Soc\left(b\right)\le a\wedge b$. Since $b$ is a soc-supplement of $a$ in $L$, we have $1=a\vee b$ and $a\wedge b\le Soc\left(b\right)$. Thus $a\wedge b=Soc\left(b\right)$. Hence $Soc\left(b\right)=a\wedge b$ is a minimal essential element in $[0,b]$.

Theorem 8

Let $L$ be a modular lattice. If every element in $L$ is a soc-s-element, then $L$ is a soc-a-s-lattice.

Proof

Let $a,b\in L$ be such that $a\vee b=1$. We have $a\wedge b\le b$ and since $b$ is a soc-s-element. Let $c\in L$ be such that $c\le b$, $b=(a\wedge b)\vee c$ and $(a\wedge b)\wedge c\le Soc\left(c\right)$. Thus $a\wedge c\le Soc\left(c\right)$. Also $1=a\vee b=a\vee [(a\wedge b)\vee c]=a\vee c.$ Thus $1=a\vee c$ and $a\wedge c\le Soc\left(c\right)$ imply $L$ is a soc-a-s-lattice.

Definition 13

A lattice $L$ is said to be a soc-weakly supplemented lattice if for any element $a\in L$, $a\ne 0,1$ there exists $b\in L$ such that $a\vee b=1$ and $a\wedge b\le Soc\left(1\right)$. In short we say that $L$ is a soc-w-s-lattice.

An element $a\in L$ is called soc-weak-supplement if $a$ is a soc-weak-supplement of some element $b\in L$.

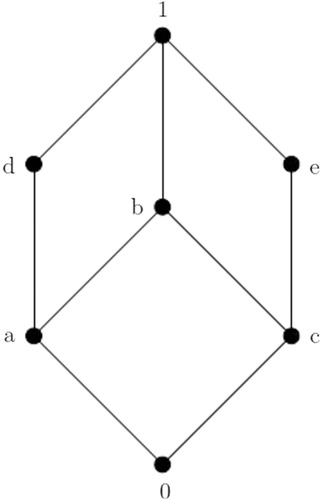
Example 6

Every complemented lattice is a soc-w-s-lattice.

Example 7

In the lattice $L$ shown in Fig. 3, for elements $f,h\in L$ such that $f\vee h=1$ but $d=f\wedge h\nleqq Soc\left(1\right)=a$ that is $d\nleqq a$. Hence $L$ is not a soc-w-s-lattice.

short-legendFig. 3

The following lemma is an analogue of Proposition 9.8 from Anderson and Fuller [9].

Lemma 9

Let $L$ and $L^{\prime }$ be two lattices and $f:L\to L^{\prime }$ be a homomorphism satisfying $f\left({\vee }_{i\in I}{a}_i\right)={\vee }_{i\in I}f\left(a_i\right)$ then $f\left(Soc\left(1\right)\right)\le Soc\left(1^{\prime }\right)$ for $1\in L$ and $1^{\prime }\in L^{\prime }$.

Proof

For $1\in L$ and $1^{\prime }\in L^{\prime }$, $Soc\left(1\right)$ $=\vee ($all atoms of $L)$ and

$Soc\left(1^{\prime }\right)$ $=\vee ($all atoms of $L^{\prime })$. Now, $f\left(Soc\left(1\right)\right)=f[\vee \left(\text{all atoms of}L\right)]=\vee \left[f\left(\text{all atoms of}L\right)\right]=Soc\left(1^{\prime }\right).$Hence, $f\left(Soc\left(1\right)\right)\le Soc\left(1^{\prime }\right)$.

We show that a homomorphic image of a Soc-w-s-lattice is a Soc-w-s-lattice under a condition.

Theorem 10

Let $L$ be a lattice satisfying $f\left({\vee }_{i\in I}{a}_i\right)={\vee }_{i\in I}f\left(a_i\right)$. Then any homomorphic image of a soc-w-s-lattice is a soc-w-s-lattice.

Proof

Let $f:L\to L^{\prime }$ be an epimorphism and $L$ be a soc-w-s-lattice. To show: $L^{\prime }$ is a soc-w-s-lattice. Let $a\in L^{\prime }$ then $f^{-1}\left(a\right)\le L$. Since $L$ is a soc-w-s-lattice, $f^{-1}\left(a\right)$ has a soc-weak-supplement $b\in L$, that means $L=f^{-1}\left(a\right)\vee b$ and $f^{-1}\left(a\right)\wedge b\le soc\left(1\right)$. Then $f\left(f^{-1}\left(a\right)\right)\vee f\left(b\right)=f\left(1\right)=1^{\prime }\in L^{\prime }$ imply $1^{\prime }=a\vee f\left(b\right)$. Now, $a\wedge f\left(b\right)=f(f^{-1}\left(a\right)\wedge b)\le f\left(Soc\left(1\right)\right)\le Soc\left(1^{\prime }\right)\left(\text{by Lemma 9}\right).$

Thus $1^{\prime }=a\vee f\left(b\right)$ and $a\wedge f\left(b\right)\le Soc\left(1^{\prime }\right)$ implies $L^{\prime }$ is a soc-w-s-lattice.

Lemma 11

Let $L$ be an atomistic lattice and $a,b\in L$. If $a\le b$, then

$Soc\left(a\right)=a\wedge Soc\left(b\right)$.

Proof

Let $a\le b$. It is clear that $Soc\left(a\right)\le a\wedge Soc\left(b\right)$. Let $x\le a\wedge Soc\left(b\right)$. Since $L$ is atomistic,

$x=\vee q_i:q_i$ is an atom of $L$ and $q_i\le x$. Now, $x\le a$ implies $q_i\le a$ for all $q_i\le x$. Then $x\le \vee q_i\le Soc\left(a\right)$. Thus $Soc\left(a\right)=a\wedge Soc\left(b\right)$.

Theorem 12

Let $L$ be an atomistic modular lattice. If $L$ is a soc-w-s-lattice then every supplement element of $L$ is a soc-w-s-element.

Proof

Suppose that $a\in L$ is a supplement in $L$. Since $L$ is a soc-w-s-lattice, for any element $b\in L$ such that $b\le a$, there exists $c\in L$ such that $b\vee c=1$ and $b\wedge c\le Soc\left(1\right)$. Now, by modularity, we get $a=a\wedge 1=a\wedge [b\vee c]=b\vee [a\wedge c]$ and $b\wedge (a\wedge c)=a\wedge (b\wedge c)\le a\wedge Soc\left(1\right)=Soc\left(a\right)\le Soc\left(1\right)$ by Lemma 11. Thus $a=b\vee (a\wedge c)$ and $b\wedge (a\wedge c)\le Soc\left(1\right)$ imply $a$ is a soc-w-s-element.

The following result is analogue of Lemma 2.18 from Tohidi [2].

Theorem 13

Let $L$ be a modular lattice, $a,b\in L$ and $a$ be a soc-w-s-element. If $a\vee b$ has a soc-w-supplement in $L$, then so does $b$.

Proof

Let $a\vee b$ have a soc-w-supplement in $L$, then there exists $c\in L$ such that $(a\vee b)\vee c=1$ and $(a\vee b)\wedge c\le Soc\left(1\right)$. Since $a$ is a soc-w-s-element and $(c\vee b)\wedge a\le a$, there exists $d\in L$ such that $d\le a$, $a=[(c\vee b)\wedge a]\vee d$ and $[(c\vee b)\wedge a]\wedge d\le Soc\left(a\right)$ that is $(c\vee b)\wedge d\le Soc\left(a\right)$. Now, by modularity, we get

$1=a\vee b\vee c=[(c\vee b)\wedge a]\vee d\vee b\vee c=a\wedge [(c\vee b)\vee d]\vee (b\vee c)=(b\vee c\vee a)\wedge (c\vee b\vee d)=(c\vee b)\vee d=(c\vee d)\vee b$

and

$(c\vee d)\wedge b\le (c\vee d)\wedge (d\vee b)\wedge (c\vee b)\le (d\vee b)\wedge (c\vee d)\wedge (c\vee b)\le [(d\vee b)\wedge c]\vee d\wedge (c\vee b)\le [c\wedge (d\vee b)]\vee [d\wedge (c\vee b)]\le Soc\left(1\right)\vee Soc\left(a\right)\le Soc\left(1\right).$

Thus $c\vee d$ is a soc-w-supplement of $b$ in $L$.

Theorem 14

Let $L$ be a modular lattice and $1=a\vee b$, $a,b\in L$. If $a$ and $b$ are soc-w-s-elements, then $L$ is a soc-w-s-lattice.

Proof

Let $c\in L$ such that $a\vee b\vee c=1$ and let $a\vee b\vee c$ have a soc-w-supplement 0 in $L$. Then by Theorem 13, $a\vee c$ has a soc-w-supplement in $L$. Again by Theorem 13, $c$ has a soc-w-supplement in $L$. Hence $L$ is soc-w-s-lattice.

Theorem 15

Every soc-a-s-lattice is a soc-s-lattice and every soc-s-lattice is a soc-w-s-lattice.

Proof

Let $L$ be a soc-a-s-lattice. To show: $L$ is a soc-s-lattice. Let $a,b\in L$ such that $a\vee b=1$.

We claim: $a\wedge b\le Soc\left(b\right)$.

Since $L$ is a soc-a-s-lattice, there exists $c\in L$ such that $c\le b$, $1=a\vee c$ and $a\wedge c\le Soc\left(c\right)$. Now, $a\wedge c\le a\wedge b\le Soc\left(c\right)\le Soc\left(b\right)$. Thus $a\wedge b\le Soc\left(b\right)$. Hence $L$ is a soc-s-lattice.

Next, let $L$ be a soc-s-lattice. To prove: $L$ is soc-w-s-lattice. Let $a\in L$. Since $L$ is a soc-s-lattice, there exists $b\in L$ such that $a\vee b=1$ and $a\wedge b\le Soc\left(b\right)$. Now $a\wedge b\le Soc\left(b\right)\le Soc\left(1\right)$ that is $a\wedge b\le Soc\left(1\right)$. Hence $L$ is soc-w-s-lattice.

Remark 2

The following example shows that the converse of the above theorem need not be true.

Example 8

The lattice $L$ shown in Fig. 2 is a soc-w-s-lattice but not a soc-a-s-lattice. Since, for $e,f\in L$, $1=e\vee f$, here $c\le f$ but $c$ is not a soc-supplement of $e$ because $c\vee e\ne 1$. Hence $L$ is not a soc-a-s-lattice.

4 Soc-$\oplus$-supplemented-lattices, completely soc-$\oplus$-supplemented-lattices and lattices satisfying the summand intersection property

Definition 14

A lattice $L$ is called a soc-$\oplus$-supplemented-lattice if every element $a\in L$ has a soc-supplement $b\in L$ such that $1=b\oplus c$, for some $c\in L$. In short we say that $L$ is a soc-$\oplus$-s-lattice.

Example 9

Every complemented lattice is a soc-$\oplus$-s-lattice.

Example 10

In the lattice $L$ shown in Fig. 4, $d\vee b=1$. Here $b$ is a soc-supplement of $d$, but $b$ is not a direct summand of 1. Hence $L$ is not a soc-$\oplus$-s-lattice.

short-legendFig. 4

The following theorem is an analogue of Lemma 3.1 from Tohidi [2].

Theorem 16

Let $L$ be a modular lattice and $a,b\in L$ be such that $a\vee b$ has a soc-supplement $c\in L$ in $L$ and $a\wedge (b\vee c)$ has a soc-supplement $d\in L$ in $a$. Then $c\vee d$ is a soc-supplement of $b$ in $L$.

Proof

Let $c$ be a soc-supplement of $a\vee b$ in $L$ and $d$ be a soc-supplement of $a\wedge (b\vee c)$ in $a$. Then $(a\vee b)\vee c=1$ with $(a\vee b)\wedge c\le Soc\left(c\right)$ and $[a\wedge (b\vee c)]\vee d=a$ with $[a\wedge (b\vee c)]\wedge d\le Soc\left(d\right)$ that is $(b\vee c)\wedge d\le Soc\left(d\right)$. Now, by modularity, we get

$1=a\vee b\vee c=[(c\vee b)\wedge a]\vee d\vee b\vee c=a\wedge [(c\vee b)\vee d]\vee (b\vee c)=(b\vee c\vee a)\wedge (c\vee b\vee d)=c\vee b\vee d=b\vee (c\vee d)$

and

$(c\vee d)\wedge b\le (c\vee d)\wedge (d\vee b)\wedge (c\vee b)\le (d\vee b)\wedge (c\vee d)\wedge (c\vee b)\le [(d\vee b)\wedge c]\vee d\wedge (c\vee b)\le [c\wedge (d\vee b)]\vee [d\wedge (c\vee b)]\le Soc\left(c\right)\vee Soc\left(d\right)\le Soc(c\vee d).$

Thus $1=(c\vee d)\vee b$ and $(c\vee d)\wedge b\le Soc(c\vee d)$ imply $c\vee d$ is a soc-supplement of $b$ in $L$.

Theorem 17

Let $L$ be a modular lattice, $a,b\in L$ be soc- $\oplus$-s-elements and $1=a\oplus b$. Then $L$ is a soc- $\oplus$-s-lattice.

Proof

Let $c\in L$. Then $a\vee b\vee c=1$ such that $a\vee b\vee c$ has trivially soc-supplement $0$ in $L$. Let $d\in L$ be a soc-supplement of $b\wedge (a\vee c)$ in $b$, so that $d$ is a direct summand of $b$. Then by Theorem 16, $d$ is a soc-supplement of $a\vee c$ in $L$. Let $e$ be a soc-supplement of $a\wedge (c\vee d)$ in $a$ such that $e$ is a direct summand of $a$. Again by Theorem 16, we have $d\vee e$ is a soc-supplement of $c$ in $L$. Since $d$ is a direct summand of $b$ and $e$ is a direct summand of $a$ then $e\oplus d=e\vee d$ is a direct summand of $1$. Hence $L$ is a soc-$\oplus$-s-lattice.

Definition 15

A lattice $L$ is said to be completely soc-$\oplus$-s-lattice if every direct summand of $1$ other than an atom is a soc-$\oplus$-s-element.

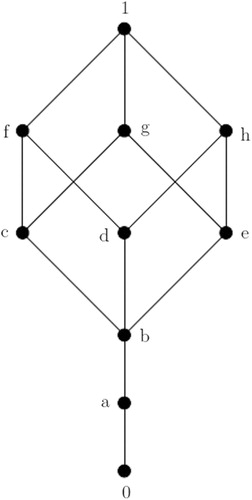
Example 11

In the lattice $L$ shown in Fig. 5, direct summands $e$ and $f$ of 1 which are not atoms are soc-$\oplus$-s-elements. For example, $e\in L$ with $e=a\vee b$ such that $a\wedge b=0,Soc\left(b\right)=b$ and $0\le b$, here $b$ is a soc-supplement of $a$ in $e$ which is a direct summand of $e$. Hence $L$ is a completely soc-$\oplus$-s-lattice.

short-legendFig. 5

Example 12

In the lattice shown in Fig. 4, direct summands $d$ and $e$ of 1 which are not atoms are not soc-$\oplus$-s-element because there is no such $w,x,y,z\in L$ such that $d=w\vee x$ and $e=y\vee z$. Hence $L$ is not a completely soc-$\oplus$-s-lattice.

The concept of the summand intersection property is known in module theory, see Akalan, Birkenmeier and Tercan [10].

The concept of the summand intersection property is also known in lattice theory, see Nimbhorkar and Shroff [11].

Definition 16

A lattice $L$ satisfies Summand Intersection Property (SIP), if for any direct summands $a,b\in L$ of 1, $a\wedge b$ is also a direct summand of $1$.

Theorem 18

Let $L$ be a modular lattice. Suppose that $L$ is a soc- $\oplus$-s-lattice satisfying $SIP$. Then $L$ is a completely soc- $\oplus$-s-lattice.

Proof

Let $a\in L$ be a direct summand of 1. To show: $a$ is a soc-$\oplus$-s-element. Let $b\le a$. Since $L$ is soc-$\oplus$-s-lattice, there exists a soc-supplement $c\in L$ of $b$ such that $b\vee c=1$, $b\wedge c\le Soc\left(c\right)$ and $c\oplus d=1$. Now, by modularity, we get $a=a\wedge 1=a\wedge (b\vee c)=b\vee (c\wedge a)$. Since $L$ satisfies the property $SIP$, $a\wedge c$ is a direct summand of 1. So $b\wedge (a\wedge c)=b\wedge c$, $b\wedge c\le Soc\left(c\right)\le Soc\left(1\right)$ that is $b\wedge c\le Soc\left(1\right)$ and $b\wedge c\le a\wedge c$. Therefore, $b\wedge c\le (a\wedge c)\wedge Soc\left(1\right)=Soc(a\wedge c)$. Thus $a\wedge c$ is a soc-supplement of $b$ in $a$ which is a direct summand of $a$. Hence $a$ is a soc-$\oplus$-s-lattice.

Notes

Peer review under responsibility of Kalasalingam University.