On edge-graceful labeling and deficiency for regular graphs

Peer review under responsibility of Kalasalingam University.

Abstract

An edge-graceful labeling of a finite simple graph with $p$ vertices and $q$ edges is a bijection from the set of edges to the set of integers $\{1,2,\dots ,q\}$ such that the vertex sums are pairwise distinct modulo $p$, where the vertex sum at a vertex is the sum of labels of all edges incident to such vertex. A graph is called edge-graceful if it admits an edge-graceful labeling. In 2005 Hefetz (2005) proved that a regular graph of even degree is edge-graceful if it contains a 2-factor consisting of $m{C}_n$, where $m,n$ are odd. In this article, we show that a regular graph of odd degree is edge-graceful if it contains either of two particular 3-factors, namely, a claw factor and a quasi-prism factor. We also introduce a new notion called edge-graceful deficiency, which is a parameter to measure how close a graph is away from being an edge-graceful graph. In particular the edge-graceful deficiency of a regular graph of even degree containing a Hamiltonian cycle is completely determined.

Keywords:

• Edge-graceful
• Edge-graceful deficiency
• Claw factor
• Quasi-prism
• Hamiltonian cycle

1 Introduction and background

All graphs in this paper are finite simple, undirected, and without loops unless otherwise stated. In 1990, N. Hartsfield and G. Ringel [1] introduced the concepts called antimagic labeling and antimagic graphs.

Definition 1

Let $G=(V,E)$ be a graph with $p$ vertices, $q$ edges, and without any isolated vertex. An antimagic edge labeling is a bijection $f:E\to \{1,2,\dots ,q\}$, such that the induced vertex sum $f^{+}:V\to {\mathbb{Z}}^{+}$ given by $f^{+}\left(u\right)=\sum \{f\left(uv\right):uv\in E\}$ is injective. A graph is called antimagic if it admits an antimagic labeling. If moreover for $G$ the vertex sums $f^{+}$ are consecutive integers, we say $G$ admits an $(a,1)$-antimagic labeling and $G$ is an $(a,1)$-antimagic graph.

Definition 2

Let $G=(V,E)$ be a graph with $p$ vertices, $q$ edges, and without any isolated vertex. An edge-graceful edge labeling is a bijection $f:E\to \{1,2,\dots ,q\}$, such that the induced vertex sum $f^{+}:V\to {\mathbb{Z}}_p$ given by $f^{+}\left(u\right)=\sum \{f\left(uv\right):uv\in E\}\left(modp\right)$ is injective. A graph is called edge-graceful if it admits an edge-graceful labeling.

Note that an $(a,1)$-antimagic labeling is an edge-graceful labeling, and an edge-graceful labeling is necessarily an antimagic labeling.

In 1985 S.P. Lo [2] introduced such notion of edge-graceful labeling. In 2005 D. Hefetz [3] proved that, for an edge-graceful graph $G$, it is still edge-graceful after adding an arbitrary even factor. In 2008, T.-M. Wang [4] studied edge-graceful spectrum of graphs. Most recently M. Bača et al. [5] studied the existence for $(a,1)$-antimagic-ness of certain 3-regular graphs. Many various types of graphs have been shown to be antimagic [3–15^{[3][4][5][6][7][8][9][10][11][12][13][14][15]}] over the years. For more conjectures and open problems on various types of antimagic labeling problems, interested readers can refer to the dynamic survey article of J. Gallian [16].

In this paper, we show that an odd regular graph is edge-graceful if it contains a quasi-prism factor or a claw factor. Also a more general concept called edge-graceful deficiency is introduced, and we completely determine the edge-graceful deficiency of Hamiltonian regular graphs of even degree.

2 Odd regular graphs with a quasi-prism factor

The following is a necessary condition for a graph $G$ to be an edge-graceful graph:

Lemma 3

[2]

Let $G$ be a graph with $p$ vertices and $q$ edges. If $G$ is edge-graceful, then $q(q+1)\equiv \frac{p(p-1)}{2}\left(modp\right)$.

In 2005 D. Hefetz [3] proved the following:

Lemma 4

D. Hefetz [3]

Assume $H$ is a graph which is obtained from a graph $G$ by adding an arbitrary even factor. If $G$ is edge-graceful, then $H$ is edge-graceful.

According to the 2-factorization of an even regular graph by Petersen [17], the edge-graceful-ness of regular graphs can be reduced to the study of that of 2-regular graphs and 3-regular graphs. D. Hefetz mentioned the following sufficient condition for edge-graceful even regular graphs:

Corollary 5

D. Hefetz [3]

Assume $H$ is an even regular graph which contains a $2$-factor consisting of $m{C}_n$, where $m,n$ are odd. Then $H$ is edge-graceful.

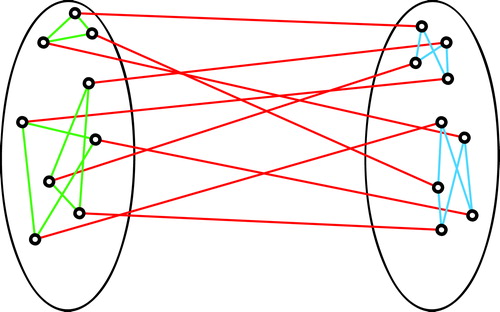
In this section we show that an odd regular graph is edge-graceful if it contains a quasi-prism factor, which is a particular 3-regular spanning subgraph. It is clear that a 3-regular graph has even number of vertices. We define quasi-prisms as follows:

Definition 6

A quasi-prism $G(U,V)$ is a 3-regular graph with $2k$ vertices $U=\{u_1,u_2,\dots ,u_k\}$ and $V=\{v_1,v_2,\dots ,v_k\}$, which consists of the edge-disjoint union of a 1-factor and two $2$-regular subgraphs induced by $U$ and $V$ respectively. (See Fig. 1.)

Fig. 1 An example of a quasi-prism.

The generalized Petersen graphs $GP(n,k)$ are examples of quasi-prisms $G(U,V)$ for which 2-regular subgraphs induced by $U$ and $V$ are defined as follows.

Definition 7

Let $n$, $k$ be integers such that $n\ge 3$ and $1\le$ $k$ $\le$ $\lfloor \frac{n-1}{2}\rfloor$. The generalized Petersen graph $GP(n,k)$ is defined by $V\left(GP(n,k)\right)=\{u_i,v_i|1\le i\le n\}$, and $E\left(GP(n,k)\right)=\{u_i{u}_{i+1},u_i{v}_i,v_i{v}_{i+k}|1\le i\le n\}$ where the subscripts are taken modulo $n$. (See Fig. 2.) We call $u_1,u_2,\dots ,u_n$ an outer cycle, and $v_1,v_2,\dots ,v_n$ an inner cycle.

Fig. 2 Generalized Petersen graphs.

Now, we are in a position to show the following:

Theorem 8

All quasi-prisms are edge-graceful.

Proof

We have a convention that the notation $[a,b]$ stands for the set of all integers between $a$ and $b$ (inclusive), namely, $\{a,a+1,\dots ,b\}$. Let $G(U,V)$ be a quasi-prism with $4n$ vertices and $6n$ edges. Also let $G(U,V)$ be the 3-regular graph with $4n$ vertices $U=\{u_1,u_2,\dots ,u_{2n}\}$ and $V=\{v_1,v_2,\dots ,v_{2n}\}$, which consists of the edge-disjoint union of a 1-factor and two $2$-regular subgraphs induced by $U$ and $V$ respectively. We denote by $G\left[U\right]$ and $G\left[V\right]$ these two $2$-regular subgraphs induced by $U$ and $V$ respectively and denote the edge set of the 1-factor by $\{u_i{v}_i:1\le i\le 2n\}$. In the following in order to obtain the required edge-graceful labeling we label edges over the 1-factor with integers within $[n+1,3n]$, label edges over $G\left[U\right]$ with integers within $[3n+1,5n]$, and label edges over $G\left[V\right]$ with integers within $[1,n]\cup [5n+1,6n]$.

For the purpose of labeling, we assign an orientation so that, over each connected component (connected 2-cycle) of $G\left[U\right]$ and $G\left[V\right]$, the flow direction is either clockwise or counter-clockwise. Then we denote the edges of $G\left[U\right]$ by $e_{out}\left(u_i\right)$ and $e_{in}\left(u_i\right)$ respectively to be the outgoing edge label from the vertex $u_i$ and the incoming edge label to the vertex $u_i$ according to the given orientation. Similarly we denote the edges of $G\left[V\right]$ by $e_{out}\left(v_i\right)$ and $e_{in}\left(v_i\right)$ respectively. Note that there is a one-to-one correspondence between $\{e_{out}\left(u_i\right):1\le i\le 2n\}$ and $\{e_{in}\left(u_i\right):1\le i\le 2n\}$, also an one-to-one correspondence between $\{e_{out}\left(v_i\right):1\le i\le 2n\}$ and $\{e_{in}\left(v_i\right):1\le i\le 2n\}$. In fact these bijections are valid even restricted to each connected cycle with the fixed orientation.

Then we may start labeling by the following steps.

Step 1. First we label edges $\{u_i{v}_i:1\le i\le 2n\}$ over the 1-factor with integers within $[n+1,3n]$ in a bijective fashion. Then we denote $w_m\left(u_i\right)$ and $w_m\left(v_i\right)$ the partial vertex sums thus far at the vertices $u_i$ and $v_i$ respectively contributed by the above given edge labeling over $u_i{v}_i$.

Step 2. Then we label the edges over $G\left[U\right]$ using the following rule for $1\le i\le 2n$: $e_{in}\left(u_i\right)=6n+1-w_m\left(u_i\right).$

Let $w\left(u_i\right)$ be the vertex sum at the vertex $u_i$ via adding all incident edge labels. Therefore, $w\left(u_i\right)=e_{in}\left(u_i\right)+w_m\left(u_i\right)+e_{out}\left(u_i\right)=6n+1+e_{out}\left(u_i\right)$, hence the vertex sums over $G\left[U\right]$ is $[n+2,3n+1]$ modulo $4n$.

Step 3. We label the edges over $G\left[V\right]$ using the following rule for $1\le i\le 2n$:

Step 3-1. If $n+1\le w_m\left(v_i\right)\le 2n$, label the edges over $G\left[V\right]$ using the rule: $e_{in}\left(v_i\right)=3n+1-w_m\left(v_i\right).$

Step 3-2. If $2n+1\le w_m\left(v_i\right)\le 3n$, label the edges over $G\left[V\right]$ using the rule: $e_{in}\left(v_i\right)=7n+1-w_m\left(v_i\right).$

Let $w\left(v_i\right)$ be the vertex sum at the vertex $v_i$ via adding all incident edge labels. Therefore, it can be calculated and seen that the vertex sums over $G\left[V\right]$ is $[1,n+1]\cup [3n+2,4n]$ modulo $4n$.

Finally it may be seen that, from the above steps we have the desired edge-graceful labeling and the proof is complete.   $■$

Therefore, by the above result combined with Lemma 4 by Hefetz [3], one sees immediately that any odd regular graph containing a quasi-prism factor is edge-graceful.

Most recently M. Bača et al. [5] showed the existence of $(a,1)$-antimagic-ness for certain regular graphs, which are examples of edge-graceful graphs. However these results naturally lead one to ask the following general question comparing edge-graceful-ness and $(a,1)$-antimagic-ness: Does there exist any graph which is edge-graceful but not $(a,1)$-antimagic? As far as we know, the complete graph $K_4$ is not $(a,1)$-antimagic, but is edge-graceful. This fact shows that the set of $(a,1)$-antimagic graphs is properly contained in the set of edge-graceful graphs.

In fact it is interesting to answer the following:

Problem 9

Determine all 2-regular graphs/3-regular graphs which are not $(a,1)$-antimagic, but are edge-graceful.

3 Odd regular graphs with a claw factor

In this section we study another sufficient condition for an edge-graceful regular graphs of odd degree, namely, containing a claw factor.

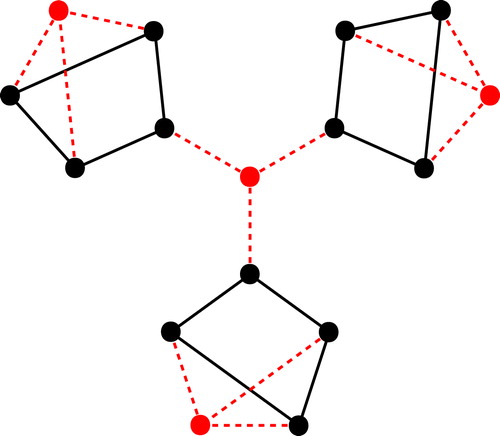
There is a well known cubic graph without any perfect matching as shown in Fig. 3, given by J. Petersen as a related example for the fact that if a cubic graph is bridgeless then it admits a perfect matching. It is noticed the example can be treated as a factorization of one claw factor as explained below and one degenerate 2-factor and can be shown to be edge-graceful. We extend this fact to a more general situation in the following. We define a claw factor as a spanning subgraph consisting of vertex disjoint $K_{1,3}$’s, as seen in Fig. 3.

Fig. 3 A cubic graph without any perfect matching but with a claw factor.

We are then in a position to show the following.

Theorem 10

Let $G$ be a 3-regular graph with $4n$ vertices and $6n$ edges. Suppose $G$ contains a claw factor, that is, $G$ can be decomposed into the union of a claw factor $C$ and a 2-regular subgraph induced by all pendant vertices of the claws in $C$. Then $G$ is edge-graceful.

Proof

Note that $G$ has the claw factor consisting of $n$ vertex disjoint claws, which is named as $K\left(i\right)$ for $1\le i\le n$. Let the center vertex of $K\left(i\right)$ of degree 3 be $v_i$ for $1\le i\le n$ and all other pendant vertices be $u_j$ for $1\le j\le 3n$.

We use $1,2,\dots ,3n$ to label the edges of 2-regular subgraph induced by all pendant vertices of the claws in $C$, and use the rest $3n+1,3n+2,\dots ,6n$ to label the edges of the claw factor $C$. Precisely we label the three edges of the claw $K\left(i\right)$ by $3n+i,4n+i,6n+1-i$ for $1\le i\le n$. Therefore the vertex sum at the vertex $v_i$ is $13n+i+1$ for $1\le i\le n$, namely $13n+2,13n+3,\dots ,14n+1$.

On the other hand, in order to label the edges over $E\left(G\right)-E\left(C\right)$ properly, we put orientations over each connected cycle component either clockwise or counterclockwise. Then define the outgoing edge label at the vertex $u_j$ by $f^{out}\left(u_j\right)=6n+1-w\left(u_j\right)$ for $1\le j\le 3n$, where $w\left(u_j\right)$ is the partial vertex sum while labeling the edges of claws in $C$, thus $w\left(u_j\right)$ ranges from $3n+1,3n+2,\dots$ to $6n$. Therefore, the vertex sums over $u_j$ are $6n+1+j$ for $1\le j\le 3n$, namely $6n+2,6n+3,\dots ,9n+1$. Combined with the vertex sums over $v_i$ for $1\le i\le n$, that is $13n+2,13n+3,\dots ,14n+1$, we may see immediately that $G$ is edge-graceful since the vertex sums reduced modulo $4n$ are all distinct.   $■$

Therefore by the above result combined with Lemma 4 by Hefetz [3], one concludes immediately that a regular graph of odd degree containing a claw factor is edge-graceful.

4 Edge-graceful deficiency

We define in this section a new notion edge-graceful deficiency for graphs, which is a parameter for studying those graphs which do not admit any edge-graceful labeling, and furthermore to measure how close they are away from being an edge-graceful graph.

Definition 11

The edge-graceful deficiency ${\delta }_m\left(G\right)$ of a graph $G$ is defined as the minimum value of $k$ such that the one-to-one vertex labeling $f:E\left(G\right)\to \{1,2,\dots ,q+k\}$ is edge-graceful, that is, the induced vertex sum mapping $f^{+}:V\to {\mathbb{Z}}_p$ given by $f^{+}\left(u\right)=\sum \{f\left(uv\right):uv\in E\}\left(modp\right)$ is injective. Therefore the edge-graceful deficiency of an edge-graceful graph is 0.

Note that a necessary condition for a graph with $p$ vertices and $q$ edges to be edge-graceful is $q(q+1)\equiv \frac{p(p-1)}{2}\left(modp\right)$, as deduced in Lemma 3. Thus we have the following:

Corollary 12

If the cycle $C_n$ is edge-graceful, then $n$ is odd.

Previously it was already proved that $C_n$ is edge-graceful when $n$ is odd, thus ${\delta }_m\left(C_n\right)=0$ when $n$ is odd. In below we determine completely the edge-graceful deficiency of cycles. Also as a corollary the edge-graceful deficiency of Hamiltonian regular graphs of even degree is obtained.

In order to show the above results, we start with the following general observation that, every graph $G$ of order $p\equiv 2(mod4)$ cannot be edge-graceful:

Lemma 13

Let $G$ be a graph of order $p\equiv 2(mod4)$. Then ${\delta }_m\left(G\right)=+\infty$.

Proof

Let $G$ has $q$ edges and $p=4k+2$ vertices. Assign labels $e_1,e_2,\dots ,e_q$ to edges of graph $G$, and suppose the existence of an edge-graceful labeling with the associated vertex-weights $0,1,\dots ,4k+1\left(mod(4k+2)\right)$. Consider the sum of all vertex-weights: $0+1+\cdots +(4k+1)=(4k+1)(2k+1)\left(mod(4k+2)\right)$which is also equal to $2(e_1+e_2+\cdots +e_q)$. Note that $2(e_1+e_2+\cdots +e_q)$ is even, but $(4k+1)(2k+1)\left(mod(4k+2)\right)$ is odd, a contradiction.   $■$

As a corollary we have the following:

Corollary 14

${\delta }_m\left(C_{4n+2}\right)=+\infty$.

The remaining part for edge-graceful deficiency of cycles is ${\delta }_m\left(C_{4n}\right)$, and we prove it as follows.

Lemma 15

${\delta }_m\left(C_{4n}\right)=1$ for $n\ge 1$.

Proof

Now we show that, with one extra edge label $4n+1$ allowed, there exists an $(a,1)$-antimagic labeling for $C_{4n}$, thus there exists an edge-graceful labeling for $C_{4n}$.

Let the vertex set and the edge set of $C_{4n}$ be $V\left(C_{4n}\right)=\{v_i:i=1,2,\dots ,4n\}$ and $E\left(C_{4n}\right)=\{v_i{v}_{i+1}:i=1,2,\dots ,4n-1\}\cup \left\{v_1{v}_{4n}\right\}$. If the missing value is $n+1$ then the $(a,1)$-antimagic labeling $f$ can be defined as follows: $f\left(v_1{v}_{4n}\right)=4n+1,$ $f\left(v_i{v}_{i+1}\right)=\left\{\begin{array}{cc}\frac{i+1}{2}\hfill & \text{if}i=1,3,\dots ,2n-1,\hfill \\ \frac{i+3}{2}\hfill & \text{if}i=2n+1,2n+3,\dots ,4n-1,\hfill \\ 2n+1+\frac{i}{2}\hfill & \text{if}i=2,4,\dots ,4n-2.\hfill \end{array}\right.$

Then we find that the vertex-weights form the set $\{2n+3,2n+4,\dots ,6n+2\}$, and reduced modulo $\left(4n\right)$ gives us the required result.   $■$

To summarize up, we have the following for the edge-graceful deficiency for cycles:

Theorem 16

The edge-graceful deficiency of cycles is as follows: ${\delta }_m\left(C_n\right)=\left\{\begin{array}{c}\hfill 0,n\equiv 1\left(mod2\right).\hfill \\ \hfill 1,n\equiv 0\left(mod4\right).\hfill \\ \hfill +\infty ,n\equiv 2\left(mod4\right).\hfill \end{array}\right.$

More generally, with the help of Theorem 16 and Lemma 4 by Hefetz [3], we have the following:

Theorem 17

Let $G$ be a Hamiltonian graph of order $n\ge 3$. Then the edge-graceful deficiency of $G$ is as follows: ${\delta }_m\left(G\right)=\left\{\begin{array}{c}\hfill 0,n\equiv 1\left(mod2\right).\hfill \\ \hfill 1,n\equiv 0\left(mod4\right).\hfill \\ \hfill +\infty ,n\equiv 2\left(mod4\right).\hfill \end{array}\right.$

As a corollary we have the following example for edge-graceful deficiency of the higher dimensional toroidal grids, i.e. the Cartesian product of $t$ cycles $C_{m_1}\square C_{m_2}\square \cdots \square C_{m_t},m_i\ge 3$, for each $i$. Note that $C_{m_1}\square C_{m_2}\square \cdots \square C_{m_t},m_i\ge 3$ always contains a Hamiltonian cycle.

Corollary 18

Let $m_i\ge 3$ for each $i$. Then for the higher dimensional toroidal grid $C_{m_1}\square C_{m_2}\square \cdots \square C_{m_t}$ of order $p$, one has ${\delta }_m(C_{m_1}\square C_{m_2}\square \cdots \square C_{m_t})=\left\{\begin{array}{cc}0\hfill & \text{if}p\equiv 1,3(mod4),\hfill \\ 1\hfill & \text{if}p\equiv 0(mod4),\hfill \\ +\infty \hfill & \text{if}p\equiv 2(mod4).\hfill \end{array}\right.$

5 Concluding remarks

In this article, we obtain edge-graceful labeling of regular graphs with particular types of 3-factors (odd regular graphs containing pseudo-prisms). Also the edge-graceful-ness is shown for the class of odd regular graphs with claw factors, which contains the case of certain odd regular graphs without any 1-factor.

Note that in 2005 D. Hefetz [3] proved that a regular graph of even degree is edge-graceful if it contains a $2$-factor consisting of $m{C}_n$, where $m,n$ are odd. Therefore, it is natural to ask the following:

Problem 19

Determine the edge-graceful deficiency for the $2$-regular graph $m{C}_n$, if $m$ or $n$ is even.

If Problem 19 is answered, then so is answered the edge-graceful deficiency for an arbitrary regular graph of even degree containing a 2-factor $m{C}_n$. More general we have the following:

Problem 20

Determine the edge-graceful deficiency for a general 2-regular/3-regular graph.

If Problem 20 is answered, then so is answered the edge-graceful deficiency for an arbitrary regular graph of even/odd degree, respectively.

Notes

Peer review under responsibility of Kalasalingam University.