Natural partial order on rings with involution

Peer review under responsibility of Kalasalingam University.

Abstract

In this paper, we introduce a partial order on rings with involution, which is a generalization of the partial order on the set of projections in a Rickart $\ast$-ring. We prove that a $\ast$-ring with the natural partial order forms a sectionally semi-complemented poset. It is proved that every interval $[0,x]$ forms a Boolean algebra in case of abelian Rickart $\ast$-rings. The concepts of generalized comparability $\left(GC\right)$ and partial comparability $\left(PC\right)$ are extended to involve all the elements of a $\ast$-ring. Further, it is proved that these concepts are equivalent in finite abelian Rickart $\ast$-rings.

Keywords:

• $\ast$-ring
• Partial order
• Generalized comparability
• Partial comparability

1 Introduction

An involution $\ast$ on an associative ring $R$ is a mapping such that ${(a+b)}^{\ast }=a^{\ast }+b^{\ast }$, ${\left(ab\right)}^{\ast }=b^{\ast }{a}^{\ast }$ and ${\left(a^{\ast }\right)}^{\ast }=a$ for all $a,b\in R$. A ring with an involution $\ast$ is called a $\ast$-ring. Clearly, identity mapping is an involution if and only if the ring is commutative. An element $e$ of a $\ast$-ring $R$ is a projection if $e=e^2$ and $e=e^{\ast }$. For a nonempty subset $B$ of $R$, we write $r\left(B\right)=x\in R:bx=0,\forall b\in B$, and call $r\left(B\right)$ a right annihilator of $B$ in $R$. A Rickart $\ast$-ring $R$ is a $\ast$-ring in which right annihilator of every element is generated, as a right ideal, by a projection in $R$. Every Rickart $\ast$-ring contains unity. For each element $a$ in a Rickart $\ast$-ring, there is unique projection $e$ such that $ae=a$ and $ax=0$ if and only if $ex=0$, called a right projection of $a$ denoted by $RP\left(a\right)$. In fact, $r\left(a\right)=(1-RP\left(a\right))R$. Similarly, the left annihilator $l\left(a\right)$ and the left projection $LP\left(a\right)$ are defined for each element $a$ in a Rickart $\ast$-ring $R$. The set of projections $P\left(R\right)$ in a Rickart $\ast$-ring $R$ forms a lattice, denoted by $L\left(P\left(R\right)\right)$, under the partial order ‘$e\le f$ if and only if $e=fe=ef$’. In fact, $e\vee f=f+RP\left(e(1-f)\right)$ and $e\wedge f=e-LP\left(e(1-f)\right)$. This lattice is extensively studied by I. Kaplanski [1], S. K. Berberian [2], S. Maeda in [3,4] and others.

Drazin [5] was first to introduce the $\ast$-order given by $a\underset{\ast }{⩽}b$ if and only if $a^{\ast }a=a^{\ast }b$ and $a{a}^{\ast }=b{a}^{\ast }$, which is a partial order on a semigroup with proper involution (i.e., $a{a}^{\ast }=0$ implies $a=0$). In particular, the obvious choices for $\ast$-rings with proper involution are all commutative rings with no nonzero nilpotent elements, all Boolean rings, the ring $B\left(H\right)$ of all bounded linear operators on any complex Hilbert space $H$, all Rickart $\ast$-ring. Janowitz [6] studied $\ast$-order. Thakare and Nimbhorkar [7] used $\ast$-order on a Rickart $\ast$-ring and generalized the comparability axioms to involve all elements of a $\ast$-ring. Mitsch [8] defined a partial order on a semigroup $S$ by $a{\le }_{M}b$ if and only if $a=xb=by,xa=a$ for some $x,y\in S$. We modify the order of Mitsch to have partial order on a $\ast$-ring.

In this paper, we introduce a partial order on a $\ast$-ring which is an extension of the partial order on the set of projections in a Rickart $\ast$-ring. For a $\ast$-ring $R$, it is proved that the poset $(R,\le )$ is a sectionally semi-complemented (SSC) poset. For an abelian Rickart $\ast$-ring, we prove that every interval $[0,x]$ is an orthomodular poset, in fact, an orthomodular lattice. In the last section, comparability axioms are introduced to involve all elements of the $\ast$-ring.

2 Natural partial order and its properties

We introduce the following order on a $\ast$-ring with unity.

Definition 2.1

Let $R$ be a $\ast$-ring with unity. Define a relation $\le$ on $R$ by $a\le b$ if and only if $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$, for some $x\in R$.

Note that, $a\le b$ with the above order implies $a{\le }_{M}b$, where ${\le }_M$ is Mitsch partial order. For, let $x\in R$ be such that $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$. Then for $y=x^{\ast }$ we get $a=xb=by$, $xa=a$, i.e., $a{\le }_{M}b$.

Proposition 2.2

Let $R$ be a $\ast$-ring with unity. Then the relation $\le$ given in Definition 2.1 is a partial order on $R$.

Proof

Reflexive: for $x=1$, we have $a=xa=a{x}^{\ast }$. Hence $a\le a,\forall a\in R$.

Antisymmetric: Let $a\le b$ and $b\le a$. Then there exist $x,y\in R$ such that $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$ and $b=yb=ya=b{y}^{\ast }=a{y}^{\ast }$, hence $b=ya=y\left(b{x}^{\ast }\right)=b{x}^{\ast }=a$.

Transitive: Let $a\le b$ and $b\le c$. Hence there exist $x,y\in R$ such that $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$ and $b=yb=yc=b{y}^{\ast }=c{y}^{\ast }$. Then $\left(xy\right)a=\left(xy\right)\left(b{x}^{\ast }\right)=x\left(yb\right)x^{\ast }=xb{x}^{\ast }=a{x}^{\ast }=a,\left(xy\right)c=x\left(yc\right)=xb=a,a{\left(xy\right)}^{\ast }=\left(xb\right)\left(y^{\ast }{x}^{\ast }\right)=x\left(b{y}^{\ast }\right)x^{\ast }=xb{x}^{\ast }=a{x}^{\ast }=a$ and $c{\left(xy\right)}^{\ast }=c\left(y^{\ast }{x}^{\ast }\right)=\left(c{y}^{\ast }\right)x^{\ast }=b{x}^{\ast }=a$. Hence $a\le c$. □

Henceforth $\mathbf{R}$ denotes a $\ast$-ring with unity and we say that $a\le b$ through $x$ whenever $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$.

Note 2.3

If we restrict this partial order to the set of projections in a Rickart $\ast$-ring, then it coincides with the usual partial order for projections given in Berberian [2].

Remark 2.4

This order is generally different from the $\ast$-order.

For, let $a=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 2\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right],b=\left[\begin{array}{cc}\hfill 2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\in R=M_2\left({\mathbb{Z}}_3\right)$with transpose as an involution. Since $R$ is a Rickart $\ast$-ring, the $\ast$-order on $R$ does exist.

Then $a^{\ast }a=\left[\begin{array}{cc}\hfill 2\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right]=a^{\ast }b$, $a{a}^{\ast }=\left[\begin{array}{cc}\hfill 2\hfill & \hfill 2\hfill \\ \hfill 2\hfill & \hfill 2\hfill \end{array}\right]=b{a}^{\ast }$, hence $a\underset{\ast }{⩽}b$.

Next let $x=\left[\begin{array}{cc}\hfill x_1\hfill & \hfill x_2\hfill \\ \hfill x_3\hfill & \hfill x_4\hfill \end{array}\right]$be such that $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$. Then $a=xa$ gives

$\left[\begin{array}{cc}\hfill 1\hfill & \hfill 2\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill x_1\hfill & \hfill x_2\hfill \\ \hfill x_3\hfill & \hfill x_4\hfill \end{array}\right]\left[\begin{array}{cc}\hfill 1\hfill & \hfill 2\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill x_1+x_2\hfill & \hfill 2(x_1+x_2)\hfill \\ \hfill x_3+x_4\hfill & \hfill 2(x_3+x_4)\hfill \end{array}\right]$and $a=a{x}^{\ast }$ gives

$\left[\begin{array}{cc}\hfill 1\hfill & \hfill 2\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 2\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right]\left[\begin{array}{cc}\hfill x_1\hfill & \hfill x_3\hfill \\ \hfill x_2\hfill & \hfill x_4\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill x_1+2x_2\hfill & \hfill x_3+2x_4\hfill \\ \hfill x_1+2x_2\hfill & \hfill x_3+2x_4\hfill \end{array}\right]$.

On comparing, we get $x_1+x_2=1=x_1+2x_2$, which gives $x_2=0,x_1=1$. Similarly $x_3+x_4=1,x_3+2x_4=2$, giving $x_3=0,x_4=1$, i.e., $x=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$. But $xb\ne a$. Hence $a\nleqq b$. On the other hand, if $c=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill \end{array}\right],d=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill \end{array}\right]$ and $y=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$, then $c\le d$ through $y$. While $c^{\ast }c\ne c^{\ast }d$, hence $c\underset{\ast }{\nleqq }d$. Thus these two partial orders (natural partial order and $\ast$-order) are distinct. In fact, the two orders are incomparable.

Proposition 2.5

Let $R$ be a commutative $\ast$-ring. Then $a\le b$ implies $a\underset{\ast }{⩽}b$.

Proof

Let $a\le b$. Then there exists $x\in R$ such that $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$. This yields $a^{\ast }b={\left(xa\right)}^{\ast }b=a^{\ast }{x}^{\ast }b=a^{\ast }\left(b{x}^{\ast }\right)=a^{\ast }a$ and since $R$ is commutative, we get $a{a}^{\ast }=b{a}^{\ast }$. Hence $a\underset{\ast }{⩽}b$. □

Note that the converse of the implication in the above proposition is not true in general, since $\ast$-order is not a partial order on ${\mathbb{Z}}_{12}$ with identity mapping as an involution. Indeed $6^{\ast }.6=6^{\ast }.0=0^{\ast }.0$, so $\ast$-order is not antisymmetric.

In the next result, we provide properties of the natural partial order.

Theorem 2.6

Let $R$ be a $\ast$-ring with unity. Then the following statements hold.

(1)	0 is the least element of the poset $R$.

(2)	If $h$ is a central projection, then $ha\le a,\forall a\in R$.

(3)	$a\le e,a\in R,e\in P\left(R\right)$ implies $a\in P\left(R\right)$.

(4)	$a\le b$ if and only if $a^{\ast }\le b^{\ast }$.

(5)	If $a\le b$, then $r\left(b\right)\subseteq r\left(a\right)$ and $l\left(b\right)\subseteq l\left(a\right)$.

(6)	$a\le b,$ $b$ regular (i.e., $b{b}^{\prime }b=b$ for some $b^{\prime }\in R$) imply $a$ is regular.

(7)	$a\le b$ and $a$ has the right (resp. left) inverse imply $a=b$, i.e., every element having the right (resp. left) inverse is maximal.

(8)	The following statements are equivalent: (a) For any $a,b\in R$, if $a\le b$ then $ac\le bc$ for all $c\in R$. (b) For any $a,b\in R$, if $a\le b$ then $ca\le cb$ for all $c\in R$.

Proof

$\left(1\right)$ and $\left(2\right)$ are obvious.

$\left(3\right)$ Suppose $a\le e,e\in P\left(R\right)$. Let $a\le e$ through $x$ for some $x\in R$, i.e., $a=xa=xe=a{x}^{\ast }=e{x}^{\ast }$. This yields $a^2=xe.e{x}^{\ast }=xe{x}^{\ast }=a{x}^{\ast }=a$. Also, $a^{\ast }={\left(xe\right)}^{\ast }=e{x}^{\ast }=a$, hence $a\in P\left(R\right).$

$\left(4\right)$ Let $a\le b$. Then $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$ for some $x\in R$. Hence $a^{\ast }=x{a}^{\ast }=a^{\ast }{x}^{\ast }=b^{\ast }{x}^{\ast }=x{b}^{\ast }$ which gives $a^{\ast }\le b^{\ast }$. The converse follows from the fact that ${\left(a^{\ast }\right)}^{\ast }=a$.

$\left(5\right)$ Obvious.

$\left(6\right)$ Suppose $a\le b$ and $b$ is regular, i.e., $b{b}^{\prime }b=b$ for some $b^{\prime }\in R$. Let $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$ for some $x\in R$. Then $a=a{x}^{\ast }=xb{x}^{\ast }=xb{b}^{\prime }b{x}^{\ast }=\left(xb\right)b^{\prime }\left(b{x}^{\ast }\right)=a{b}^{\prime }a$. Hence $a$ is regular.

$\left(7\right)$ Let $c\in R$ be such that $ac=1$ (resp. $ca=1$) and $a\le b$. Let $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$ for some $x\in R$. Then $a=xa$ (resp. $a=a{x}^{\ast }$) gives $ac=xac$ (resp. $ca=ca{x}^{\ast }$). Thus $1=x$ (resp. $1=x^{\ast }$). Hence $a=b$, i.e, $a$ is a maximal element.

$\left(8\right)$ $\left(a\right)\Rightarrow \left(b\right)$ Suppose $a\le b$. By $\left(4\right)$ above, we have $a^{\ast }\le b^{\ast }$. By assumption, $a^{\ast }{c}^{\ast }\le b^{\ast }{c}^{\ast }$ for any $c^{\ast }\in R$, which gives ${\left(ca\right)}^{\ast }\le {\left(cb\right)}^{\ast }$. Again by $\left(4\right)$ above, we have $ca\le cb$ for any $c\in R$.

$\left(b\right)\Rightarrow \left(a\right)$ Follows similarly. □

In a poset $P$, the principal order ideal generated by $a\in P$ is given by $\left(a\right]=x\in P:x\le a$.

Proposition 2.7

If $a$ and $b$ are central elements of a $\ast$-ring $R$ which generate the same ideals of a ring $R$, then there is an order isomorphism between the set of elements $\le a$ and the set of elements $\le b$.

Proof

Let $a$ and $b$ be central elements with $Ra=Rb$. Then $a=bs,b=at$ for some $s,t\in R$. Denote $\left(a\right]=x\in R:x\le a$. Define $\varphi :\left(a\right]\to \left(b\right]$ by $\varphi \left(x\right)=xt$. We claim that $xt\le b,\forall x\in \left(a\right]$. As $x\le a$, we have $x=x_{1}x=x_{1}a=a{x}_1^{\ast }=x{x}_1^{\ast }$ for some $x_1\in R$. Then $x_{1}xt=xt$, $xt{x}_1^{\ast }=x_{1}at{x}_1^{\ast }=x_{1}b{x}_1^{\ast }=x_1{x}_1^{\ast }b=x_1{x}_1^{\ast }at=x_{1}a{x}_1^{\ast }t=x_{1}xt=xt$, $x_{1}b=x_{1}at=xt$ and $b{x}_1^{\ast }=x_1^{\ast }b=x_1^{\ast }at=a{x}_1^{\ast }t=xt$. Hence $xt\le b$. Now, let $x,y\in \left(a\right]$ be such that $x=x_{1}x=x_{1}a=a{x}_1^{\ast }=x{x}_1^{\ast }$ and $y=y_{1}y=y_{1}a=a{y}_1^{\ast }=y{y}_1^{\ast }$ for some $x_1,y_1\in R$. Then $\varphi \left(x\right)=\varphi \left(y\right)$ if and only if $xt=yt$ if and only if $x_{1}at=y_{1}at$ if and only if $x_{1}b=y_{1}b$ if and only if $x_{1}a=y_{1}a$ if and only if $x=y$. Hence $\varphi$ is well defined and one-to-one. Let $z\in \left(b\right]$. Then as above $zs\in \left(a\right]$ and $z=z_{1}b=z_{1}z=b{z}_1^{\ast }=z{z}_1^{\ast }$ for some $z_1\in R$. Also $\varphi \left(zs\right)=zst=z_{1}bst=z_{1}at=z_{1}b=z$, i.e., $\varphi$ is a bijection.

Now, suppose that $x,y\in \left(a\right]$ with $x\le y$. Then $x=x_{1}x=x_{1}a=a{x}_1^{\ast }=x{x}_1^{\ast }$, $y=y_{1}y=y_{1}a=a{y}_1^{\ast }=y{y}_1^{\ast }$ and $x=x_{2}x=x_{2}y=y{x}_2^{\ast }=x{x}_2^{\ast }$, for some $x_1,x_2,y_1\in R$. Next, $\left(x_1{x}_2\right)xt=x_{1}xt=xt$, $\left(x_1{x}_2\right)yt=x_{1}xt=xt$, $xt{\left(x_1{x}_2\right)}^{\ast }=xt{x}_2^{\ast }{x}_1^{\ast }=x_{1}at{x}_2^{\ast }{x}_1^{\ast }=x_{1}b{x}_2^{\ast }{x}_1^{\ast }=x_1{x}_2^{\ast }{x}_1^{\ast }b=x_1{x}_2^{\ast }{x}_1^{\ast }at=a{x}_1{x}_2^{\ast }{x}_1^{\ast }t=x{x}_2^{\ast }{x}_1^{\ast }t=x{x}_1^{\ast }t=xt$and $yt{\left(x_1{x}_2\right)}^{\ast }=yt{x}_2^{\ast }{x}_1^{\ast }=y_{1}at{x}_2^{\ast }{x}_1^{\ast }=y_{1}b{x}_2^{\ast }{x}_1^{\ast }=y_1{x}_2^{\ast }{x}_1^{\ast }b=y_1{x}_2^{\ast }{x}_1^{\ast }at=y_{1}a{x}_2^{\ast }{x}_1^{\ast }t=y{x}_2^{\ast }{x}_1^{\ast }t=x{x}_1^{\ast }t=xt$. Consequently $\varphi \left(x\right)\le \varphi \left(y\right)$. This implies that $\varphi$ is an order isomorphism. In fact, $\psi :\left(b\right]\to \left(a\right]$ defined by $\psi \left(y\right)=ys$, works as an inverse of $\varphi$. In the same manner we can prove that for $u,v\in \left(b\right],u\le v$ implies $\psi \left(u\right)\le \psi \left(v\right)$. Now, suppose that $\varphi \left(x\right)\le \varphi \left(y\right)$. Then $\varphi \left(x\right),\varphi \left(y\right)\in \left(b\right]$, so $\psi \left(\varphi \left(x\right)\right)\le \psi \left(\varphi \left(y\right)\right)$, that is $x\le y$. □

Theorem 2.8

Condition of Compatibility

If $xa=a{x}^{\ast }$, $\forall a,x\in R$, then the natural partial order is compatible with multiplication.

Proof

In view of Theorem 2.6 (8), it is enough to show that $a\le b$ implies $ac\le bc,\forall c\in R$. Let $a\le b$, then there exists $x\in R$ such that $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$. Hence $ac=xac=xbc=a{x}^{\ast }c=b{x}^{\ast }c$, i.e., $ac=xac$, $ac{x}^{\ast }=c{a}^{\ast }{x}^{\ast }=c{\left(xa\right)}^{\ast }=c{a}^{\ast }=ac$. Also $bc{x}^{\ast }=c{b}^{\ast }{x}^{\ast }=c{\left(xb\right)}^{\ast }=c{a}^{\ast }=ac$, hence $ac\le bc$. □

Definition 2.9

Two elements $a$ and $b$ in a $\ast$-ring $R$ are orthogonal, denoted by $a\perp b$, if there exists $x\in R$ such that $xa=a=a{x}^{\ast }$ and $xb=0=b{x}^{\ast }$.

The orthogonality relation in a $\ast$-ring has the following properties.

Theorem 2.10

For elements $a,b,c$ in a $\ast$-ring $R$ , the following statements hold.

(1)	$a\perp a$ implies $a=0$.

(2)	$a\perp b$ if and only if $b\perp a$ if and only if $a\perp (-b)$.

(3)	$a\perp b$, $c\le a$ imply $c\perp b$.

(4)	$a\perp b$ if and only if $a\le a-b$.

(5)	$a\le b$ implies $b-a\le b$ and $b-a\perp a$.

(6)	If $a\perp b$, then $a\wedge b=0$ and $a+b$ is an upper bound of both $a,b$.

(7)	$a\perp b$, $(a+b)\perp c$ imply $a\perp (b+c)$.

Proof

$\left(1\right),\left(2\right)$ Obvious.

$\left(3\right)$ Suppose that $a\perp b$ and $c\le a$. Let $x,y\in R$ be such that $a=xa=a{x}^{\ast }$, $xb=0=b{x}^{\ast }$ and $c=yc=c{y}^{\ast }=ya=a{y}^{\ast }$. Then $\left(yx\right)c=yxa{y}^{\ast }=ya{y}^{\ast }=c{y}^{\ast }=c$. Similarly, $c{\left(yx\right)}^{\ast }=c$. On the other hand, $\left(yx\right)b=0$ and $b{\left(yx\right)}^{\ast }=0$. Consequently, $c\perp b$.

$\left(4\right)$ Suppose $a$ and $b$ are orthogonal. Let $x\in R$ be such that $a=xa=a{x}^{\ast }$ and $xb=0=b{x}^{\ast }$. Then $a=x(a-b)=(a-b)x^{\ast }=xa=a{x}^{\ast }$, hence $a\le a-b$. Conversely, suppose that $a\le a-b$. Let $x\in R$ be such that $a=x(a-b)=(a-b)x^{\ast }=xa=a{x}^{\ast }$. Then $a=x(a-b)$ and $a=xa$ gives $xb=0$. Similarly, $b{x}^{\ast }=0$. Hence $a\perp b$.

$\left(5\right)$ Let $x\in R$ be such that $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$. Then $(1-x)(b-a)=b-a-xb+xa=b-a-a+a=b-a$, $(1-x)b=b-xb=b-a$, $b{(1-x)}^{\ast }=b-b{x}^{\ast }=b-a$ and $(b-a){(1-x)}^{\ast }=b-a-b{x}^{\ast }+a{x}^{\ast }=b-a-a+a=b-a$. Hence $b-a\le b$. Also $(1-x)(b-a)=b-a=(b-a){(1-x)}^{\ast }$ and $(1-x)a=0=a{(1-x)}^{\ast }$. Hence $b-a\perp a$.

$\left(6\right)$ Suppose $a\perp b$ and $x$ be such that $xa=a=a{x}^{\ast },xb=0=b{x}^{\ast }$. Let $c\le a$ and $c\le b$ i.e. $c=x_{1}c=x_{1}a=c{x}_1^{\ast }=a{x}_1^{\ast }$ and $c=x_{2}c=x_{2}b=c{x}_2^{\ast }=b{x}_2^{\ast }$ for some $x_1,x_2\in R$. Then $x_{1}a=c=x_{2}b$ gives $c=x_{1}a=x_{2}b=x_{1}a{x}^{\ast }=x_{2}b{x}^{\ast }=0$. Hence $a\wedge b=0$. From $\left(2\right)$, $\left(4\right)$ and $\left(5\right)$, we have $a\le a+b$ and $b=(a+b)-a\le a+b$.

$\left(7\right)$ Suppose that $a\perp b$, $(a+b)\perp c$. From $\left(6\right)$, we have $a\le a+b$ and $a+b\le a+b+c$. This gives $a\le a+b+c$. Then from $\left(5\right)$, we get $(b+c)\perp a$, as required. □

A poset $P$ with 0 is called sectionally semi-complemented (in brief SSC) if, for $a,b\in P$, $0<a<b$, there exists an element $c\in P$ such that $0<c<b$ and ${a,c}^l=0$, where ${a,c}^l=x\in P:x\le a\text{and}x\le c$. Thus from $\left(5\right)$ and $\left(6\right)$ of Theorem 2.10, we have the following result.

Theorem 2.11

Let $R$ be a $\ast$-ring. Then the poset $(R,\le )$ is an SSC poset.

A ring is called an abelian ring if all of its idempotents are central.

Lemma 2.12

Let $R$ be an abelian Rickart $\ast$-ring. If $a\le b$, then there exists a projection $e$ such that $a=ae=be$.

Proof

Suppose $a\le b$, then there exists $x\in R$ such that $a=xa=xb=a{x}^{\ast }=b{x}^{\ast }$. Since $a=xa$, we have $(1-x)a=0$. This gives $a\in r1-x=eR$ for some projection $e\in R$. Then $ea=a=ae$ and $(1-x)e=0$, i.e., $e=xe=e{x}^{\ast }$. Also, $a=xb$ implies $ea=exb=xeb=eb$. Thus $a=ae=be$. □

Proposition 2.13

In an abelian Rickart $\ast$-ring $R$, the following statements are equivalent.

(i)

$a\le b$.

(ii)	There exists $x\in R$ such that $a=ax=bx$.

(iii)

$ab=a^2$.

Proof

(i)$\Rightarrow$ ii) Follows from Lemma 2.12.

(ii)$\Rightarrow$ iii) Let $a=ax=bx$. Then $ax-bx=0$ gives $(a-b)x=0$, hence $RP(a-b)x=0$. Since $R$ is abelian, $xRP(a-b)=0$. Hence $x(a-b)=0$ giving $xa=xb$. Now consider $ab=\left(ax\right)b=a\left(xb\right)=a\left(xa\right)=a^2$.

(iii)$\Rightarrow$ i) Let $ab=a^2$, i.e., $a(b-a)=0$. Then $RP\left(a\right)$ is a projection such that $a=RP\left(a\right)a$ and $RP\left(a\right)(b-a)=0$, i.e., $RP\left(a\right)b=RP\left(a\right)a=a$, hence $a\le b$. □

As a consequence of the above result for abelian Rickart $\ast$-rings, our partial order is equivalent to Abian’s partial order given by $a\le b$ if and only if $ab=a^2$ in [9].

Lemma 2.14

If $R$ is an abelian Rickart $\ast$-ring, then $a\perp b$ implies $a\wedge b=0$ and $a\vee b=a+b$.

Proof

Suppose $a\perp b$. By Theorem 2.10 $\left(6\right)$, $a\wedge b=0$ and $a+b$ is an upper bound of $a$ and $b$. Let $a\le c$ and $b\le c$, then there exist projections $e,f$ such that $a=ea=ec$ and $b=fb=fc$. Since $a\perp b$, there exists $x\in R$ such that $xa=a=a{x}^{\ast }$ and $xb=0=b{x}^{\ast }$. Let $y=ex+f(1-x)$. Then $y(a+b)=exa+exb+f(1-x)a+f(1-x)b=a+b$, $(a+b)y^{\ast }=a+b$, $yc=exc+f(1-x)c=a+b$ and $c{y}^{\ast }=a+b$, i.e., $a+b\le c$. Thus $a\vee b=a+b.$ □

Before proceeding further, we need the definition of orthomodular poset. An orthomodular poset is a partially ordered set $P$ with 0 and 1 equipped with a mapping $x\to x^{\perp }$ (called the orthocomplementation) satisfying the following conditions.

(i)	$a\le b\Rightarrow b^{\perp }\le a^{\perp }$,

(ii)	${\left(a^{\perp }\right)}^{\perp }=a$ for all $a\in P$,

(iii)

$a\vee a^{\perp }=1$ and $a\wedge a^{\perp }=0,$ for all $a\in P$,

(iv)	$a\le b^{\perp }$ implies that $a\vee b$ exists in $P$,

(v)	$a\le b\Rightarrow b=a\vee {(a\vee b^{\perp })}^{\perp }$.

The following result is essentially due to Marovt et al.[10, Theorem 1].

Theorem 2.15

Let $R$ be a Rickart $\ast$-ring. Then $a\underset{\ast }{⩽}b$ if and only if there exist projections $p$ and $q$ such that $a=pb=bq$.

In an abelian Rickart $\ast$-ring any idempotent is a projection. Recall the definition of the minus partial order in a Rickart ring, originally introduced in [11]: $a{\le }^{-}b$ if and only if $a=pb=bq$ for some idempotents $p$ and $q$. Hence, in an abelian Rickart $\ast$-ring we have $a{\le }^{-}b$ if and only if $a=RP\left(a\right)b=bRP\left(a\right)$, so by Theorem 2.15, we conclude that $a{\le }^{-}b$ implies $a{\le }^{\ast }b$. Now, from the above considerations and from Proposition 2.13 and Theorem 2.15, it follows that the natural partial order, the star partial order and the minus partial order are equivalent in any abelian Rickart $\ast$-ring.

We know that, if $R$ is a Rickart $\ast$-ring, then the set of projections $P\left(R\right)$ forms a lattice and the set $e\in P\left(R\right):e\le x^{\prime \prime }$ is a sublattice of $P\left(R\right)$, where $x^{\prime }$ is a projection which generates the right annihilator of $x$.

Theorem 2.16

In an abelian Rickart $\ast$-ring $R$ every interval $[0,x]$ is ortho-isomorphic to $e\in P\left(R\right):e\le x^{\prime \prime }.$ Hence every interval $[0,x]$ is a Boolean algebra.

Proof

The first assertion follows from Lemma 4 in [6] and in abelian case, $P\left(R\right)$ is Boolean. □

3 Comparability axioms

Two projections $e$ and $f$ are said to be equivalent, written $e\sim f$, if there is $w\in eRf$ such that $e=w{w}^{\ast }$ and $f=w^{\ast }w$. The relation $\sim$ is an equivalence relation on the set of projections in a Rickart $\ast$-ring. A projection $e$ is said to be dominated by a projection $f$ if $e\sim g\le f$, for some projection $g$ in $R$. We write $e\lesssim f$ to mean that $e$ is dominated by a projection $f$. Two projections $e$ and $f$ are said to be generalized comparable if there exists a central projection $h$ such that $he\lesssim hf$ and $(1-h)f\lesssim (1-h)e$. A $\ast$-ring is said to satisfy the generalized comparability $\left(GC\right)$ if any two projections are generalized comparable. Two projections $e$ and $f$ are said to be partially comparable if there exist non zero projections $e_0$, $f_0$ in $R$ such that $e_0\le e$, $f_0\le f$ and $e_0\sim f_0$. If for any pair $e,f$ of projections in $R$, $eRf\ne 0$ implies $e$ and $f$ are partially comparable, then $R$ is said to satisfy partial comparability ($PC$). More about comparability axioms on the set of projections in a Rickart $\ast$-ring can be found in Berberian [2].

Drazin [5] extended the relation of equivalence of two projections to arbitrary elements of a $\ast$-ring as follows.

Definition 3.1

[5, Definition 2*]

Let $R$ be a $\ast$-ring with unity. We say that $a\sim b$ if and only if there exists $x\in aRb,y\in bRa$ such that $a{a}^{\ast }=x{x}^{\ast },b{b}^{\ast }=y{y}^{\ast },a^{\ast }a=y^{\ast }y,b^{\ast }b=x^{\ast }x$.

This relation is symmetric on a $\ast$-ring. Thakare and Nimbhorkar [7] extended the comparability axioms using the above relation and $\ast$-order to involve all elements of a Rickart $\ast$-ring.

We provide a relation which is symmetric and transitive on arbitrary elements of a $\ast$-ring as an extension of the relation of equivalence of two projections.

Definition 3.2

Let $R$ be a $\ast$-ring with unity. We say that $a\sim b$ if and only if there exists $x,y\in R$ such that $a{a}^{\ast }=x{x}^{\ast },b{b}^{\ast }=y{y}^{\ast },a^{\ast }a=y^{\ast }y,b^{\ast }b=x^{\ast }x$ with $x=ax=xb$ and $y=by=ya$.

Now, we extend the concepts of dominance, $GC,PC$ etc. from the set of projections in a Rickart $\ast$-ring to general elements in a $\ast$-ring.

Definition 3.3

(1)	Let $R$ be a $\ast$-ring with unity. We say that $a$ is dominated by $b$ if $a\sim c\le b$ for some $c\in R$. In notation $a\lesssim b$.

(2)	A $\ast$-ring $R$ is said to satisfy the generalized comparability for elements ($GC$), if for any $a,b\in R$ there exists a central projection $h$ such that $ha\lesssim hb$ and $(1-h)b\lesssim (1-h)a$.

(3)

Two elements $a,b$ in a $\ast$-ring $R$ are said to be partially comparable if there exists two non-zero elements $c,d$ in $R$ such that $c\le a,d\le b$ with $c\sim d$. A $\ast$-ring $R$ is said to satisfy the partial comparability for elements ($PC$), if for any $a,b\in R$, $aRb\ne 0$ implies $a$ and $b$ are partially comparable.

Clearly, if $a\le b$ or $a\sim b$, then $a\lesssim b$.

Lemma 3.4

If $a\lesssim b$ and $h$ is a central projection, then $ha\lesssim hb$.

Definition 3.5

Two elements $a$ and $b$ in a $\ast$-ring $R$ are said to be very orthogonal if there exists a central projection $h$ such that $ha=a$ and $hb=0$.

The relevance of very orthogonality to generalized comparability is as follows (an analogous result for projections is proved in [2]):

Theorem 3.6

If $a$ and $b$ are elements of a $\ast$-ring $R$, then the following statements are equivalent.

(i)	$a$ and $b$ are generalized comparable.

(ii)	There exists orthogonal decompositions $a=x+y$, $b=z+w$ with $x\sim z$, $y$ and $w$ are very orthogonal.

Proof

(i) $\Rightarrow$ (ii) Suppose $a$ and $b$ are generalized comparable. Let $h$ be a central projection such that $ha\lesssim hb$ and $(1-h)b\lesssim (1-h)a$. Then $ha\sim k_1\le hb$, $(1-h)b\sim k_2\le (1-h)a$, for some $k_1,k_2\in R$. Hence $k_1=m_1{k}_1=m_{1}hb=k_1{m}_1^{\ast }=hb{m}_1^{\ast },$ for some $m_1\in R$. Then $k_1=m_{1}hb$ gives $k_{1}h=m_{1}hbh=m_{1}hb=k_1$. Similarly, $k_2=(1-h)k_2$. Also $ha{k}_2^{\ast }=ha(1-h)k_2^{\ast }=0={\left(ha\right)}^{\ast }{k}_2$, $(1-h)b{k}_1^{\ast }={\left[(1-h)b\right]}^{\ast }{k}_1=0$.

We claim that $ha+k_2\sim k_1+(1-h)b$. Since $ha\sim k_1$, there exist $x_1,y_1\in R$ such that $\left(ha\right){\left(ha\right)}^{\ast }=x_1{x}_1^{\ast },k_1{k}_1^{\ast }=y_1{y}_1^{\ast },{\left(ha\right)}^{\ast }\left(ha\right)=y_1^{\ast }{y}_1$ and $k_1^{\ast }{k}_1=x_1^{\ast }{x}_1$ with $x_1=ha{x}_1=x_1{k}_1$ and $y_1=k_1{y}_1=y_{1}ha$. Clearly, $x_1=h{x}_1$ and $y_1=h{y}_1$, since $k_{1}h=k_1$. Similarly, since $(1-h)b\sim k_2$, there exist $x_2,y_2\in R$ such that $k_2{k}_2^{\ast }=x_2{x}_2^{\ast },\left[(1-h)b\right]{\left[(1-h)b\right]}^{\ast }=y_2{y}_2^{\ast },k_2^{\ast }{k}_2=y_2^{\ast }{y}_2$ and ${\left[(1-h)b\right]}^{\ast }\left[(1-h)b\right]=x_2^{\ast }{x}_2$ with $x_2=k_2{x}_2=x_2(1-h)b$ and $y_2=(1-h)b{y}_2=y_2{k}_2$. Clearly, $x_2=(1-h)x_2$ and $y_2=(1-h)y_2$, since $k_2(1-h)=k_2$.

Let $x=x_1+x_2$ and $y=y_1+y_2$. Since $h{k}_2=0$ and $(1-h)k_1=0$, we have $(ha+k_2)x=(ha+k_2)(x_1+x_2)=ha{x}_1+ha{x}_2+k_2{x}_1+k_2{x}_2=x_1+0+0+x_2=x$, $x[k_1+(1-h)b]=(x_1+x_2)[k_1+(1-h)b]=x_1{k}_1+x_1(1-h)b+x_2{k}_1+x_2(1-h)b=x_1+0+0+x_2=x$. Similarly, we have $y=[k_1+(1-h)b]y=y(ha+k_2)$.

Also, $x{x}^{\ast }=(x_1+x_2){(x_1+x_2)}^{\ast }=x_1{x}_1^{\ast }+x_1{x}_2^{\ast }+x_2{x}_1^{\ast }+x_2{x}_2^{\ast }=x_1{x}_1^{\ast }+0+0+x_2{x}_2^{\ast }=\left(ha\right){\left(ha\right)}^{\ast }+k_2{k}_2^{\ast }=[ha+k_2]{[ha+k_2]}^{\ast }$ and $x^{\ast }x={(x_1+x_2)}^{\ast }(x_1+x_2)=x_1^{\ast }{x}_1+x_1^{\ast }{x}_2+x_2^{\ast }{x}_1+x_2^{\ast }{x}_2=x_1^{\ast }{x}_1+0+0+x_2^{\ast }{x}_2=k_1^{\ast }{k}_1+{\left[(1-h)b\right]}^{\ast }\left[(1-h)b\right]={[k_1+(1-h)b]}^{\ast }[k_1+(1-h)b]$. On the other hand, $y{y}^{\ast }=(y_1+y_2){(y_1+y_2)}^{\ast }=y_1{y}_1^{\ast }+y_1{y}_2^{\ast }+y_2{y}_1^{\ast }+y_2{y}_2^{\ast }=k_1{k}_1^{\ast }+0+0+\left[(1-h)b\right]{\left[(1-h)b\right]}^{\ast }=[k_1+(1-h)b]{[k_1+(1-h)b]}^{\ast }$ and $y^{\ast }y={(y_1+y_2)}^{\ast }(y_1+y_2)=y_1^{\ast }{y}_1+y_1^{\ast }{y}_2+y_2^{\ast }{y}_1+y_2^{\ast }{y}_2=y_1^{\ast }{y}_1+0+0+y_2^{\ast }{y}_2={\left(ha\right)}^{\ast }\left(ha\right)+k_2^{\ast }{k}_2={[ha+k_2]}^{\ast }[ha+k_2]$. Therefore $ha+k_2\sim k_1+(1-h)b$.

Next, we claim that $ha+k_2\le a$ and $k_1+(1-h)b\le b$. Since $h$ is a central projection, $k_2\le (1-h)a\le a$ and $ha\le a$, implies $k_2=x_1{k}_2=x_{1}a=k_2{x}_1^{\ast }=a{x}_1^{\ast }$ and $ha=x_{2}ha=x_{2}a=ha{x}_2^{\ast }=a{x}_2^{\ast }$, for some $x_1,x_2\in R$. Let $y_1=x_1+h{x}_2$. Then $y_1(ha+k_2)=x_{1}ha+x_1{k}_2+h{x}_{2}ha+h{x}_2{k}_2=ha+k_2$, $(ha+k_2)y_1^{\ast }=ha{x}_1^{\ast }+k_2{x}_1^{\ast }+ha{x}_2^{\ast }h+k_2{x}_2^{\ast }h=ha+k_2$ and $y_{1}a=a{(x_1+h{x}_2)}^{\ast }=ha+k_2=a{y}_1^{\ast }$, therefore $ha+k_2\le a$. Similarly, $(1-h)b+k_1\le b$. Now put $ha+k_2=x$, $(1-h)b+k_1=z$, $y=a-x$ and $w=b-z$ implies $hb-k_1=b-z=w$. Then $hw=h(hb-k_1)=hb-k_1=w$ and $hy=h(a-x)=ha-hx=ha-ha-h{k}_2=0$ (since $h{k}_2=0$), i.e., $y$ and $w$ are very orthogonal. Thus $a=x+y,b=z+w$ where $x\perp y$, $z\perp w$ such that we get $x\sim z$ with $y$ and $w$ are very orthogonal.

(ii) $\Rightarrow$ (i) Let $h$ be a central projection such that $hw=w$ and $hy=0$. Then $ha=hx+hy=hx$ and $(1-h)b=(1-h)z+(1-h)w=(1-h)z$, where $ha=hx\sim hz\le hb$ and $(1-h)b=(1-h)z\sim (1-h)x\le (1-h)a$. Thus $ha\lesssim hb$ and $(1-h)b\lesssim (1-h)a$. Hence $a,b$ are generalized comparable. □

Next result implies that $GC$ for elements is stronger than $PC$ for elements.

Theorem 3.7

Let $R$ be a $\ast$-ring with proper involution. If $R$ has $GC$ for elements, then it has $PC$ for elements.

Proof

Let $a,b$ are elements of $R$ which are not partially comparable. We will show that $aRb=0$. Applying $GC$ to the pair $a,b$ we get orthogonal decompositions $a=x+y$ and $b=z+w$, where $x\sim z$ and $y,w$ are very orthogonal. If $x\ne 0$ and $z\ne 0$ then $a$ and $b$ are partially comparable, which is a contradiction to the assumption. Also, since the involution on $R$ is proper, the case $x=0$ and $z\ne 0$ (or $x\ne 0$ and $z=0$) is impossible. Hence $x=0=z$, i.e., $a,b$ are very orthogonal. Let $h$ be a central projection such that $ha=a$ and $hb=0$. Then $aRb=haRb=aRhb=0$. Thus $R$ has $PC$ for elements. □

Lemma 3.8

In an abelian Rickart $\ast$-ring $a\perp b$ if and only if $RP\left(a\right)RP\left(b\right)=0$.

Proof

In a Rickart $\ast$-ring, $ab=0$ if and only if $RP\left(a\right)b=0$. Since all projections in $R$ are central, we get $RP\left(a\right)\in r\left(b\right)=(1-RP\left(b\right))R$. Which yields $RP\left(b\right)RP\left(a\right)=0$. Conversely, if $RP\left(a\right)RP\left(b\right)=0$, then $ab=\left(aRP\left(a\right)\right)\left(bRP\left(b\right)\right)=aRP\left(a\right)RP\left(b\right)b=0$. In fact $ab=0$ if and only if $ba=0$.

Next, suppose that $a\perp b$. Then there exists $x\in R$ such that $xa=a=a{x}^{\ast }$ and $xb=0=b{x}^{\ast }$, thus $a(1-x^{\ast })=0$. Hence $RP\left(a\right)(1-x^{\ast })=0$, this gives $RP\left(a\right)=RP\left(a\right)x^{\ast }$, i.e. $RP\left(a\right)=xRP\left(a\right)$. Since $R$ is abelian, we get $RP\left(a\right)=RP\left(a\right)x$. As $xb=0$, this yields $RP\left(a\right)b=RP\left(a\right)xb=0$. Consequently, $ab=0$. Conversely, if $ab=0$, then $RP\left(a\right)RP\left(b\right)=0$. Thus $RP\left(a\right)a=a=aRP\left(a\right)$ and $RP\left(a\right)b=0=bRP\left(a\right)$. Hence $a\perp b$. □

Thus in an abelian Rickart $\ast$-ring, $a\perp b$ if and only if $ab=0$ if and only if $ba=0$. The next result shows that the relation $\sim$ is finitely additive.

Theorem 3.9

Let $R$ be an abelian Rickart $\ast$-ring. If $a_1\perp a_2,b_1\perp b_2$ with $a_1\sim b_1$ and $a_2\sim b_2$, then $a_1+a_2\sim b_1+b_2$, i.e., the relation $\sim$ is finitely additive.

Proof

Since $a_1\perp a_2,b_1\perp b_2$, we have $RP\left(a_1\right)RP\left(a_2\right)=0=RP\left(b_1\right)RP\left(b_2\right)$. Also, $a_1\sim b_1$ and $a_2\sim b_2$ there exists $x_i,y_i\in R$ such that $a_i{a}_i^{\ast }=x_i{x}_i^{\ast },a_i^{\ast }{a}_i=y_i^{\ast }{y}_i,b_i{b}_i^{\ast }=y_i{y}_i^{\ast },b_i^{\ast }{b}_i=x_i^{\ast }{x}_i$ with $x_i=a_i{x}_i=x_i{b}_i$ and $y_i=b_i{y}_i=y_i{a}_i$ for $i=1,2$. This gives $x_i(1-a_i)=0$(since in an abelian Rickart $\ast$-ring $RP\left(x\right)=LP\left(x\right)$), hence $RP\left(x_i\right)=RP\left(x_i\right)RP\left(a_i\right)$, for $i=1,2$. Then for $i\ne j$, we have $x_i{a}_j=x_{i}RP\left(x_i\right)a_{j}RP\left(a_j\right)=x_{i}RP\left(x_i\right)RP\left(a_i\right)a_{j}RP\left(a_j\right)=x_{i}RP\left(x_i\right)RP\left(a_i\right)RP\left(a_j\right)a_j=0$. Moreover $x_i{x}_j^{\ast }=0=x_i^{\ast }{x}_j$ for $i\ne j$. Similarly, we have $b_j{x}_i=0$ for $i\ne j$.

Let $x=x_1+x_2$ and $y=y_1+y_2$. Then $(a_1+a_2)x=a_1{x}_1+a_2{x}_1+a_1{x}_2+a_2{x}_2=x_1+0+0+x_2$ and $(b_1+b_2)x=b_1{x}_1+b_1{x}_2+b_2{x}_1+b_2{x}_2=x_1+0+0+x_2=x$. Consider $x{x}^{\ast }=x_1{x}_1^{\ast }+x_2{x}_1^{\ast }+x_1{x}_2^{\ast }+x_2{x}_2^{\ast }=a_1{a}_1^{\ast }+0+0+a_2{a}_2^{\ast }=(a_1+a_2){(a_1+a_2)}^{\ast }$ and $x^{\ast }x=x_1^{\ast }{x}_1+x_2^{\ast }{x}_1+x_1^{\ast }{x}_2+x_2^{\ast }{x}_2=b_1^{\ast }{b}_1+b_1^{\ast }{b}_2={(b_1+b_2)}^{\ast }(b_1+b_2)$. Similarly, $y=(b_1+b_2)y=y(a_1+a_2)$, $y{y}^{\ast }=(b_1+b_2){(b_1+b_2)}^{\ast }$ and $y^{\ast }y={(a_1+a_2)}^{\ast }(a_1+a_2)$. Therefore $a_1+a_2\sim b_1+b_2$. □

The above result ensures that the converse of Theorem 3.7 is true for finite abelian Rickart $\ast$-rings.

Theorem 3.10

Let $R$ be a finite abelian Rickart $\ast$-ring. Then $GC$ for elements and $PC$ for elements are equivalent.

Proof

Suppose that $R$ has $PC$ for elements. It is enough to show that, $PC$ for elements implies $GC$ for elements. Let $a,b\in R$. If $aRb=0$, then $ab=0$. This gives $RP\left(a\right)b=0$. Since $R$ is an abelian ring, we get $a$ and $b$ are very orthogonal. Hence we are done. Suppose $aRb\ne 0$. Hence there exist $a_0\le a$ and $b_0\le b$ such that $a_0\sim b_0$. Let $a_1,b_1$ be the maximal elements such that $a_1\le a$, $b_1\le b$ and $a_1\sim b_1$ (since $R$ is finite, such maximal elements exist). Then $a_2=a-a_1$ and $b_2=b-b_1$ are such that $a_2\le a$, $b_2\le b$, $a_1\perp a_2$ and $b_1\perp b_2$. If $a_{2}R{b}_2\ne 0$, then by assumption, there exist $a_3\le a_2$ and $b_3\le b_2$ such that $a_3\sim b_3$. By Theorem 3.9, we get $a_1+a_3\sim b_1+b_3$. Thus $a_1\le a_1+a_3\le a$ and $b_1\le b_1+b_3\le b$ with $a_1+a_3\sim b_1+b_3$, a contradiction to maximality of $a_1$ and $b_1$. Hence $a_{2}R{b}_2=0$. This gives $a_2$ and $b_2$ very orthogonal. Thus we get an orthogonal decompositions $a=a_1+a_2$, $b=b_1+b_2$ such that $a_1\sim b_1$, $a_2$ and $b_2$ very orthogonal. By Theorem 3.6 we have $a$ and $b$ are generalized comparable. □

Proposition 3.11

Let $R$ be a $\ast$-ring with $GC$ for elements and $e$ is any projection in $R$. Then $eRe$ also has $GC$ for elements.

Proof

Let $a,b\in eRe\subseteq R$. Then there exists a central projection $h$ in $R$ such that $ha\lesssim hb$, $(1-h)b\lesssim (1-h)a$. Let $g=ehe=he\in eRe$ and $x$ be any element in $eRe$. Then $gx=hex=hx=xh=xeh=xhe=xg$. Hence $g$ is a central projection in $eRe$ with $ga=hea=ha,gb=heb=hb$, i.e., $ga\lesssim gb$ and $(e-g)b=eb-heb=b-hb=(1-h)b$, $(e-g)a=ea-hea=a-ha=(1-h)a$, i.e., $(e-g)b\lesssim (e-g)a$. Thus $a$ and $b$ are generalized comparable in $eRe$. □

Corollary 3.12

If the matrix ring $M_n\left(R\right)$ has $GC$ for elements, then $R$ has $GC$ for elements.

An ideal $I$ of a $\ast$-ring $R$ is a $\ast$-ideal if $a^{\ast }\in I$ whenever $a\in I$.

Proposition 3.13

Let $I$ be a $\ast$-ideal of $R$. If $R$ has $GC$ for elements, then $R∕I$ has $GC$ for elements.

Proof

Let $a+I$, $b+I\in R∕I$. Applying $GC$ to $a,b\in R$, there exists a central projection $h\in R$ such that $ha\lesssim hb$ and $(1-h)b\lesssim (1-h)a$. Then passing to cosets, $h+I$ is central projection in $R∕I$ such that $(h+I)(a+I)\lesssim (h+I)(b+I)$ and $[(1+I)-(h+I)](b+I)\lesssim [(1+I)-(h+I)](a+I)$. Hence $R∕I$ has $GC$ for elements. □

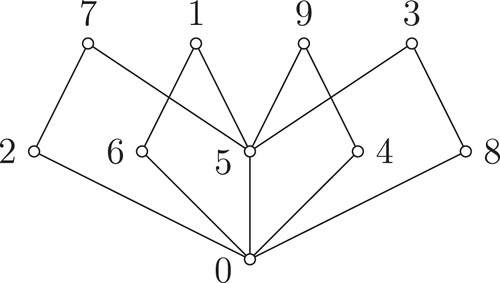
Remark 3.14

The converse of the above statement is not true. For, let $R={\mathbb{Z}}_{10}$ with the identity map as an involution and $I=0,2,4,6,8$. Then $R∕I=0+I,1+I$ which has $GC$ for elements trivially. The poset $R$ with natural partial order is depicted in Fig. 1.

Here $R$ does not have $GC$ for elements. On the contrary, if $R$ has $GC$ for elements, then by Theorem 3.7, $R$ has $PC$ for elements. Let $a=2$ and $b=4$. Then $aRb\ne 0$ and $2\nsim 4$, since $2.2^{\ast }=4$ and $4^{\ast }.4=6$ and $R$ being commutative there is no $x\in R$ such that $x{x}^{\ast }=4$ and $x^{\ast }x=6$. Hence $2$ and $4$ are not partially comparable in $R$, a contradiction.

Fig. 1 Poset of ${\mathbb{Z}}_{10}$.

Notes

Peer review under responsibility of Kalasalingam University.