Energy of a semigraph

Peer review under responsibility of Kalasalingam University.

Abstract

Semigraph is a generalization of graph. We introduce the concept of energy in a semigraph in two ways, one, the matrix energy $E_m$, as summation of singular values of the adjacency matrix of a semigraph, and the other, polynomial energy $E_{re}$, as energy of the characteristic polynomial of the adjacency matrix. We obtain some bounds for $E_m$ and show that $E_m$ is never a square root of an odd integer and $E_{re}$ cannot be an odd integer. We investigate matrix energy of a partial semigraph and change in the matrix energy due to edge deletion.

Keywords:

• Semigraph
• Matrix energy of a semigraph
• Polynomial energy of a semigraph
• Edge induced complete semigraph
• Edge induced complete closure

1 Introduction

Let $G$ be a graph of order $n$ and let $A$ be the adjacency matrix of $G$. The eigenvalues ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$ of $A$ are called eigenvalues of $G$. The energy of a graph is defined as the sum of the absolute values of its eigenvalues [1] and it is an extensively studied quantity [2,3]. There are two generalizations of graph energy. Nikiforov [4] generalized the concept of graph energy to that of the energy of any matrix. He defined the energy of a matrix $M$ as the sum of the singular values of $M$. Another generalization of the graph energy is due to Mateljevic [5] who defined the energy of an arbitrary polynomial such that Coulson integration formula remains valid.

Sampathkumar [6] generalized the definition of a graph to a semigraph in the following way.

Definition 1

A $semigraphG$ is an ordered pair of two sets $V$ and $X$, where $V$ is a non-empty set whose elements are called vertices of $G$ and $X$ is a set of $n$-tuples, called edges of $G$, of distinct vertices, for various $n$ ($n$ at least $2$) satisfying the following conditions:

1.	(SG1) — Any two edges have at most one vertex in common.

2.	(SG2) — Two edges ($u_1,u_2,\dots ,u_n$) and ($v_1,v_2,\dots ,v_m$) are considered to be equal if (a) $m=n$ and (b) either $u_i=v_i$ for $i=1,2,\dots ,n$; or $u_i=v_{n+1-i}$, for $i=1,2,\dots ,n$.

Clearly the edge $(u_1,u_2,\dots ,u_m)$ is same as $(u_m,u_{m-1},\dots ,u_1)$. For the edge $e=(u_1,u_2,\dots ,u_n)$, $u_1$ and $u_n$ are called the end vertices of $e$ and $u_2,u_3,\dots ,u_{n-1}$ are called the middle vertices of $e$. A subedge of an edge $e=(v_{i_1},v_{i_2},\dots ,v_{i_n})$ is a $k$-tuple $e^{\prime }=(v_{i_{j_1}},v_{i_{j_2}},\dots ,v_{i_{j_k}})$, where $1\le j_1<j_2<\cdots <j_k\le n$. We say that $e^{\prime }$ is the subedge induced by the set of vertices $v_{i_{j_1}},v_{i_{j_2}},\dots ,v_{i_{j_k}}$. A partial edge of $e$ is a $(k-j+1)$-tuple $e^{\prime \prime }=(v_{i_j},v_{i_{j+1}},\dots ,v_{i_k})$, where $1\le j<k\le n$. A semigraph $G^{\prime }=(V^{\prime },X^{\prime })$ is a subsemigraph (partial semigraph) of a semigraph $G=(V,X)$ if $V^{\prime }\subseteq V$ and the edges in $G^{\prime }$ are the subedges (partial edges) of the edges in $G$.

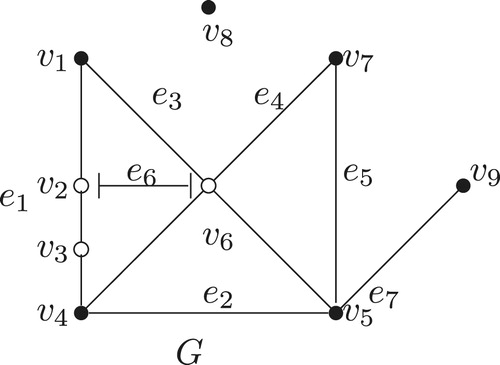
Example 1

Consider a semigraph $G=(V,X)$ in Fig. 1, where $V=v_1,v_2$, $\dots$, $v_9$ and $X=(v_1,v_2,v_3,v_4),(v_4,v_5),(v_1,v_6,v_5),(v_4,v_6,v_7)$, $(v_5,v_7),(v_2,v_6)$ , $(v_5,v_9).$ In $G$, vertices $v_1,v_4,v_5,v_7,$ and $v_9$ are the end vertices, $v_3$ is a middle vertex, $v_2$ and $v_6$ are the middle-end vertices and $v_8$ is an isolated vertex.

Fig. 1 Example of a semigraph.

The adjacency matrix of a semigraph is defined as follows [7].

Definition 2

Let $G(V,X)$ be a semigraph with vertex set $V=1,2,\dots ,m$ and edge set $X=e_1,e_2,\dots ,e_n$. The adjacency matrix of $G(V,X)$ is an $m\times m$ matrix $A\left(G\right)=\left[a_{ij}\right]$ defined as follows:

1.	for every edge $e_i$ of $X$ of cardinality, say $k$, let $e_i=(i_1,i_2,\dots ,i_k)$ such that $i_1,i_2,\dots ,i_k$ are distinct vertices in $V$, for all $i_r\in e_i;r=1,2,\dots ,k$ (a) $a_{i_1{i}_r}=r-1$ (b) $a_{i_k{i}_r}=k-r$
2.	All the remaining entries of $A\left(G\right)$ are zero.

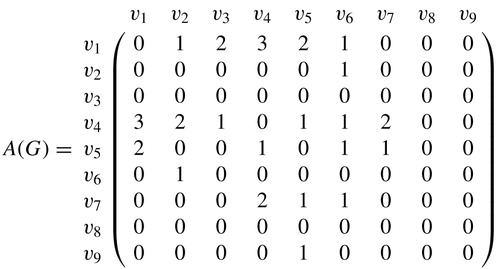
Example 2

For the semigraph $G(V,X)$ given in Fig. 1, the adjacency matrix of $G$ is

A matrix $A$ is said to be semigraphical if there exists a semigraph $G$ such that the adjacency matrix of $G$ is $A$. The cardinality of an edge $e$ is the number of vertices on that edge and is denoted by $e$. In [8], the expanse of a semigraph $G(V,X)$ is defined as $\mathcal{E}\left(G\right)=maxe-1:e\in X$. For the terms not defined here, the reader may refer to [69^[10]–11].

In this paper, we define the polynomial energy $E_{re}$ of a semigraph using the concept of energy of a polynomial. Also, we define the matrix energy $E_m$ of a semigraph using the singular values of its adjacency matrix. For the graphs, these two definitions coincide with the definition of graph energy. Bapat et al. [12] proved that the energy of a graph is never an odd integer. This holds for our definition of $E_{re}$. It has been proved that the energy of a graph is never the square root of an odd integer [13]. This holds for our definition of $E_m$. In Section 2, we obtain some bounds for $E_m$ and prove that $E_m$ is never the square root of an odd integer and in Section 3, we prove that $E_{re}$ is never an odd integer. In Section 4, we discuss the energy of partial semigraphs and change in the matrix energy due to edge deletion.

2 Matrix energy of a semigraph $E_m\left(G\right)$

Nikiforov defined the energy of a general matrix (not necessarily square) as the summation of the singular values of that matrix.

Definition 3

Let $A\left(G\right)$ be the adjacency matrix of a semigraph $G$. The matrix energy of a semigraph $G$, denoted by $E_m\left(G\right)$, is defined as the summation of the singular values of $A\left(G\right)$.

We observe the following.

1.

$A\left(G\right)A{\left(G\right)}^{\prime }$ is a positive semidefinite matrix. So its eigenvalues ${\lambda }_1,{\lambda }_2,\dots$, ${\lambda }_n$ are non-negative and therefore the singular values of $A\left(G\right)$ are non-negative real numbers. Thus, $E_m\left(G\right)\ge 0$. In fact, $E_m\left(G\right)=0$ if and only if the number of edges in $G$ is zero.

2.

If $G_1$ is a semigraph obtained by relabeling of the vertices of $G$, then $A\left(G_1\right)A{\left(G_1\right)}^{\prime }$ is obtained by interchanging the rows and the corresponding columns of $A\left(G\right)A{\left(G\right)}^{\prime }$. Therefore the eigenvalues of $A\left(G\right)A{\left(G\right)}^{\prime }$ and $A\left(G_1\right)A{\left(G_1\right)}^{\prime }$ are same and thus the singular values of $G$ and $G_1$ are same. Hence the energy $E_m$ of a semigraph is well defined.

In [14], we see that for a graph $G$ with non-empty edge set, the energy $E\left(G\right)$ of $G$ is greater or equal to 2. For a semigraph $G$, we obtain a similar bound. First, we note that if $e=(i_1,i_2,\dots ,i_k)$ is an edge of a semigraph $G$, then the principal submatrix of $A\left(G\right)$ induced by the rows and columns $i_1,i_2,\dots ,i_k$ is the adjacency matrix of the edge induced partial semigraph $G_1=〈e〉$. Let ${\sigma }_i\left(B\right),i=1,\dots ,n$, denote the singular values of a matrix $B$.

Theorem 1

If $G$ is a semigraph with nonempty edge set, then $E_m\left(G\right)\ge 2\mathcal{E}\left(G\right)$.

Proof

If the expanse of a semigraph $G$ is $k$, then there exists an edge $e\in G\left(X\right)$ with cardinality $k+1$. The adjacency matrix $A\left(〈e〉\right)$ is a principal submatrix of $A\left(G\right)$ and each of the two nonzero singular values is greater than $k$. As, ${\sum }_{i=1}^n{\sigma }_i\left(A\left(〈e〉\right)\right)\le {\sum }_{i=1}^n{\sigma }_i\left(A\left(G\right)\right)$, the result follows.

In fact, the singular values of $A\left(〈e〉\right)$ are $k\sqrt{\frac{k+1}{2}}$ and $\sqrt{\frac{k(k+1)(k+2)}{6}}$, hence $E_m\left(G\right)\ge k\sqrt{\frac{k+1}{2}}+\sqrt{\frac{k(k+1)(k+2)}{6}}$. □

From the fact that the adjacency matrix of a graph is a symmetric matrix, its singular values are same as eigenvalues. Thus for a graph $G$, its energy $E\left(G\right)$ is same as $E_m\left(G\right)$.

Corollary 1

For a graph $G$ with nonempty edge set, $E_m\left(G\right)=E\left(G\right)\ge 2$.

Proof

The result follows as $\mathcal{E}\left(G\right)=1$. □

If the cardinality of an edge $e$ of a semigraph is denoted by $k_e+1$, then clearly $k_e\ge 1$. Now we have the following lemma.

Lemma 1

If $A=A\left(G\right)$ is the adjacency matrix of a semigraph $G$ on $n$ vertices and ${\mu }_1,{\mu }_2$, $\dots ,{\mu }_n$ are the eigenvalues of $A{A}^{\prime }$, then $\sum _{i=1}^n{\mu }_i=2\sum _{e\in X}(1^2+2^2+\cdots +k_e^2).$

Proof

Corresponding to every edge $e$ of cardinality $k_e+1$, there is a sequence $1,2,\dots ,k_e$ in the rows corresponding to the end vertices of that edge. So every edge contributes $2\sum (1^2+2^2+\cdots +k_e^2)$ to the trace of $A{A}^{\prime }$.

Thus, $trace\left(A{A}^{\prime }\right)=2{\sum }_{e\in X}(1^2+2^2+\cdots +k_e^2)$.

Hence, ${\sum }_{i=1}^n{\mu }_i=2{\sum }_{e\in X}(1^2+2^2+\cdots +k_e^2)$. □

The following result gives the bounds for $E_m\left(G\right)$.

Theorem 2

For a semigraph $G$ on $n$ vertices $\sqrt{2\sum _{e\in X}(1^2+2^2+\cdots +k_e^2)}\le E_m\left(G\right)\le \sqrt{2n\sum _{e\in X}(1^2+2^2+\cdots +k_e^2)}.$

Proof

Let ${\mu }_i,i=1,2,\dots ,n$ be the eigenvalues of $A{A}^{\prime }$ and ${\sigma }_i,i=1,2,\dots ,n$ be the singular values of $A$. Consider the two vectors $({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)$ and $(1,1,\dots ,1)$. By Cauchy–Schwarz’s inequality, we have

${({\sigma }_1+{\sigma }_2+\cdots +{\sigma }_n)}^2\le n\sum _{i=1}^n{\sigma }_i^2=n\sum _{i=1}^n{\mu }_i=2n\sum _{e\in X}(1^2+2^2+\cdots +k_e^2).$

Thus, (1) $E_m{\left(G\right)}^2\le 2n\sum _{e\in X}(1^2+2^2+\cdots +k_e^2)$(1) and (2) $E_m{\left(G\right)}^2={\left(\sum _{i=1}^n{\sigma }_i\right)}^2\ge \sum _{i=1}^n{\sigma }_i^2=2\sum _{i=1}^n{\mu }_i$(2) The result follows from Eqs. $\left(1\right),\left(2\right)$ and Lemma 1. □

As $k_e=1$ for every edge of a graph, we have the following observation.

Corollary 2

If $G$ is a graph on $n$ vertices and $m$ edges, then $\sqrt{2m}\le E\left(G\right)\le \sqrt{2mn}.$

Theorem 3

For a semigraph $G$ on $n$ vertices, $E_m{\left(G\right)}^2\ge 2\sum _{e\in X}(1^2+2^2+\cdots +k_e^2)+n(n-1){\Delta }^{\frac{1}{n}},$where $\Delta =det\left(A{A}^{\prime }\right)$.

Proof

Let ${\sigma }_i,i=1,\dots ,n$, be the singular values of $G$. We have

(3) $E_m{\left(G\right)}^2={\left(\sum _{i=1}^n{\sigma }_i\right)}^2=\sum _{i=1}^n{\sigma }_i^2+2\sum _{1\le i<j\le n}{\sigma }_i{\sigma }_j=trace\left(A\left(G\right)A{\left(G\right)}^{\prime }\right)+\sum _{i\ne j}{\sigma }_i{\sigma }_j$(3)

As ${\sigma }_i$’s are non-negative numbers, so ${\sigma }_i{\sigma }_j$ are $n(n-1)$ non-negative numbers.

Therefore, arithmetic mean of ${\sigma }_i{\sigma }_j\ge$ geometric mean of ${\sigma }_i{\sigma }_j$ implies

$\frac{1}{n(n-1)}\sum _{i\ne j}{\sigma }_i{\sigma }_j\ge {\left(\prod _{i\ne j}{\sigma }_i{\sigma }_j\right)}^{\frac{1}{n(n-1)}}={\left(\prod _{i=1}^n{\sigma }_i^{2(n-1)}\right)}^{\frac{1}{n(n-1)}}={\left(\prod _{i=1}^n{\mu }_i^{(n-1)}\right)}^{\frac{1}{n(n-1)}}={\left(\prod _{i=1}^n{\mu }_i\right)}^{\frac{1}{n}}=det{\left(A{A}^{\prime }\right)}^{\frac{1}{n}}$

Thus, (4) $\sum _{i\ne j}{\sigma }_i{\sigma }_j\ge n(n-1){\Delta }^{\frac{1}{n}},$(4) where $\Delta =det\left(A{A}^{\prime }\right)$. From Eqs. (3), (4(4) $\sum _{i\ne j}{\sigma }_i{\sigma }_j\ge n(n-1){\Delta }^{\frac{1}{n}},$(4) ) and Lemma 1 the result follows. □

Corollary 3

If $G$ is a graph on $n$ vertices and $m$ edges, then $E{\left(G\right)}^2\ge 2m+n(n-1){\Delta }^{\frac{1}{n}}$.

For a matrix $A=\left[a_{ij}\right]$, the norm $\Vert A{\Vert }_2$ is defined as $\sqrt{{\sum }_{ij}{a}_{ij}^2}$. The following lemma can be seen in [4].

Lemma 2

If $A$ is any non-constant matrix and ${\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n$ are singular values of $A$, then (5) $E\left(A\right)\ge {\sigma }_1+\frac{{\Vert A\Vert }_2^2-{\sigma }_1^2}{{\sigma }_2}.$(5)

Now, we obtain a lower bound for $E_m$.

Theorem 4

If $G$ is a semigraph on $n$ vertices having largest singular value ${\sigma }_1$ and second largest singular value ${\sigma }_2$, then $E_m\left(G\right)\ge {\sigma }_1+\frac{2n\sum _{e\in X}(1^2+2^2+\cdots +k_e^2)-{\sigma }_1^2}{{\sigma }_2}.$

Proof

By substituting $A=A\left(G\right)$ and using Lemma 1 and, we get the result. □

Example 3

If $G(V,X)$ is a path semigraph, $V=1,2,\dots ,n$ and $X=e(1,2,\dots ,n)$, then the nonzero singular values of $G$ are ${\sigma }_1=(n-1)\sqrt{\frac{n}{2}}$ and ${\sigma }_2=\sqrt{\frac{(n-1)n(n+1)}{6}}$. The energy of $G$ is $E_m={\sigma }_1+\frac{2n\sum _{e\in X}(1^2+2^2+\cdots +k_e^2)-{\sigma }_1^2}{{\sigma }_2}.$Thus the bound given in Theorem 4 is attained.

Theorem 5

$E_m$ is never the square root of an odd integer.

Proof

As ${\sum }_{i=1}^n{\mu }_i=trace\left(A{A}^{\prime }\right)$, we have ${\sum }_{i=1}^n{\mu }_i=2t$, where $t={\sum }_{e\in X}(1^2+2^2+\cdots +k_e^2)$ is a positive integer. If ${\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n$ are the singular values of $A$, then (6) ${({\sigma }_1+{\sigma }_2+\cdots +{\sigma }_n)}^2=\sum _{i=1}^n{\sigma }_i^2+2\sum _{i<j}{\sigma }_i{\sigma }_j=2t+2\sum _{i<j}{\sigma }_i{\sigma }_j.$(6)

Therefore, $E_m^2=2(t+{\sum }_{i<j}{\sigma }_i{\sigma }_j)$. If $(t+{\sum }_{i<j}{\sigma }_i{\sigma }_j)$ is an integer, then $E_m^2$ is an even integer. Thus $E_m$ is never the square root of an odd integer. □

3 Polynomial energy of a semigraph $E_{re}$

The energy $E_{re}\left(\varphi \right)$ of a polynomial $\varphi$ is defined as $E_{re}\left(\varphi \right)=\sum Re\left(z_i\right)$, where $z_i$’s are the roots of $\varphi$ (see [5]). The eigenvalues of a semigraph are the zeros of the characteristic polynomial of its adjacency matrix.

Definition 4

Let $G$ be a semigraph on $n$ vertices with eigenvalues ${\lambda }_1,{\lambda }_2,\dots$, ${\lambda }_n$. The polynomial energy of the semigraph $G$, denoted by $E_{re}\left(G\right)$, is defined as $E_{re}\left(G\right)={\sum }_{i=1}^{n}Re\left({\lambda }_i\right)$.

If a semigraph $G$ is a graph, then $E_{re}=E_m={\sum }_{i=1}^n{\lambda }_i$, where ${\lambda }_i$’s are the eigenvalues of $G$.

Let $A$ and $B$ be matrices of order $m\times n$ and $p\times q$, respectively. The Krönecker product of $A$ and $B$, denoted by $A\otimes B$, is the $mp\times nq$ block matrix $\left[a_{ij}B\right]$. We have the following lemma.

Lemma 3

If $G_1$ and $G_2$ are two semigraphs of orders $m$ and $n$ respectively, and $A_1$ and $A_2$ are the adjacency matrices of $G_1$ and $G_2$ with eigenvalues ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_m$ and ${\mu }_1,{\mu }_2,\dots ,{\mu }_n$ respectively, then $A=A_1\otimes I_1+I_2\otimes A_2$ is a semigraphical matrix, where $I_1,I_2$ are the identity matrices of appropriate sizes. Further, ${\lambda }_i+{\mu }_j$, where $i=1,2,\dots ,m;j=1,2,\dots ,n$ are the eigenvalues of $A$.

Proof

Let $V_1=u_1,u_2,\dots ,u_m$ and $V_2=v_1,v_2,\dots ,v_n$ be the vertex sets of the semigraphs $G_1$ and $G_2$, respectively. Let $V=V_1\times V_2$. Consider the semigraph $G$ with vertex set $V$. $e=((u_{i_1},v_{i_1}),(u_{i_2},v_{i_2}),\dots ,(u_{i_k},v_{i_k}))$ is an edge of $G$ if and only if $(u_{i_1},u_{i_2},\dots ,u_{i_k})$ is an edge of $G_1$ and $v_{i_1}=v_{i_2}=\cdots =v_{i_k}$; or $(v_{i_1},v_{i_2},\dots ,v_{i_k})$ is an edge of $G_2$ and $u_{i_1}=u_{i_2}=\cdots =u_{i_k}$. $G$ is called the product of the semigraphs $G_1$ and $G_2$, and is denoted by $G_1\times G_2$. We observe that the adjacency matrix of $G_1\times G_2$ is $A_1\otimes I+I\otimes A_2$. Hence the eigenvalues of $G_1\times G_2$ are ${\lambda }_i+{\mu }_j$, where $i=1,2,\dots ,m;j=1,2,\dots ,n$. □

The following lemma can be seen in [9].

Lemma 4

[9]

If $\alpha$ is a zero of a monic polynomial with integer coefficients, then $\alpha$ is an integer.

Thus we have the following result.

Theorem 6

$E_{re}\left(G\right)$ is never an odd integer.

Proof

Let $A$ be the adjacency matrix of a semigraph $G$ and ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$ be the eigenvalues of $G$. Since the trace of $A$ is zero, we have (7) $\sum _{i=1}^n{\lambda }_i=0.$(7) Let ${\Lambda }^{+}$ be the set of ${\lambda }_i$’s having positive real part, and ${\Lambda }^{-}$ be the set of ${\lambda }_i$’s having negative real part.

If $x+iy$ is an eigenvalue of $G$, then $x-iy$ is also an eigenvalue of $G$. Further, both $x+iy,x-iy\in {\Lambda }^{+}$ (or ${\Lambda }^{-}$). Therefore, ${\sum }_{{\Lambda }^{+}}{\lambda }_i$ and ${\sum }_{{\Lambda }^{-}}{\lambda }_i$ are real numbers and ${\sum }_{{\Lambda }^{+}}{\lambda }_i={\sum }_{{\Lambda }^{+}}Re\left({\lambda }_i\right)$, ${\sum }_{{\Lambda }^{-}}{\lambda }_i={\sum }_{{\Lambda }^{-}}Re\left({\lambda }_i\right)$.

From Eq. (7(7) $\sum _{i=1}^n{\lambda }_i=0.$(7) ), we have ${\sum }_{{\Lambda }^{+}}{\lambda }_i+{\sum }_{{\Lambda }^{-}}{\lambda }_i=0$, that is, ${\sum }_{{\Lambda }^{+}}{\lambda }_i=-{\sum }_{{\Lambda }^{-}}{\lambda }_i$.

Suppose ${\Lambda }^{+}={\lambda }_1,{\lambda }_2,\dots ,{\lambda }_r$. Therefore (8) $E_{re}\left(G\right)=\sum _{i=1}^{n}Re\left({\lambda }_i\right)=2\sum _{{\Lambda }^{+}}Re\left({\lambda }_i\right)=2\sum _{i=1}^{r}Re\left({\lambda }_i\right).$(8) By Lemma 3, $({\lambda }_1+{\lambda }_2+\cdots +{\lambda }_r)$ is an eigenvalue of the semigraph $G\times G\times \cdots \times G$ ($r$ times). Thus $({\lambda }_1+{\lambda }_2+\cdots +{\lambda }_r)$ is a zero of a monic polynomial with integer coefficients. Therefore, if $({\lambda }_1+{\lambda }_2+\cdots +{\lambda }_r)$ is a rational number then it is an integer. Hence the result follows from Eq. (8(8) $E_{re}\left(G\right)=\sum _{i=1}^{n}Re\left({\lambda }_i\right)=2\sum _{{\Lambda }^{+}}Re\left({\lambda }_i\right)=2\sum _{i=1}^{r}Re\left({\lambda }_i\right).$(8) ). □

Not only $E_{re}\left(G\right)$ is never an odd integer, but also every even integer is a polynomial energy of some semigraph as shown in the example below.

Example 4

Consider $G(V,X)$, with vertex set $V=1,2,\dots ,k+1$ and edge set $X=e(1,2,\dots ,k+1)$. The eigenvalues of $G$ are $k,-k$. Thus, $E_{re}=2k$.

4 Matrix energy $E_m$ and partial semigraphs

For a graph $G$, we know $E\left(G\right)\ge 2$. Now we obtain a similar bound for a semigraph. It is easy to observe that if $e$ is an edge of $G$, then the adjacency matrix $A\left(e\right)$ of the edge induced partial semigraph is a principal submatrix of $A\left(G\right)$. For a semigraph $G$, let ${\sigma }_i\left(G\right)$ denote the singular values of $G$.

Theorem 7

If $G$ is a semigraph with expanse $k$, then $E_m\left(G\right)\ge 2k$.

Proof

If expanse of $G$ is $k$, then $G$ contains an edge $e$ of cardinality $k+1$. The adjacency matrix of $〈e〉$, the edge induced partial semigraph is $A\left(e\right)=\left(\begin{array}{cccccc}\hfill \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill k-1\hfill & \hfill k\hfill \\ \hfill \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \hfill & \hfill k\hfill & \hfill k-1\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right).$

The positive singular values of $A\left(e\right),{\sigma }_i\left(A\left(e\right)\right)$ are greater than $k$. Since $\sum {\sigma }_i\left(A\left(e\right)\right)\le {\sum }_{i=1}^p{\sigma }_i\left(A\left(G\right)\right)$, we have $2k\le E_m\left(G\right)$. □

Theorem 8

If $G_1$ is a partial semigraph of $G$ and $C$ is a cut set consisting of only graphical edges such that $G_1$ is a component of the semigraph obtained by deleting $C$ from $G$, then $E_m\left(G_1\right)\le E_m\left(G\right)$.

Proof

Let $G_1$ and $G_2$ be the components obtained by deleting edges of $C$ from $G$. As $G-C=G_1\cup G_2$, so $A\left(G\right)=\left[\begin{array}{ccc}\hfill \hfill & \hfill A\left(G_1\right)\hfill & \hfill X\hfill \\ \hfill \hfill & \hfill X^{\prime }\hfill & \hfill A\left(G_2\right)\hfill \end{array}\right]$, where $X=A\left(C\right)$.

Therefore, $\sum {\sigma }_i\left(A\left(G_1\right)\right)\le \sum {\sigma }_i\left(A\left(G\right)\right)$. Hence, $E_m\left(G_1\right)\le E_m\left(G\right)$. □

Corollary 4

If $e$ is a bridge, then $E_m(G-e)\le E_m\left(G\right)$.

If a bridge is deleted, the energy of a semigraph always decreases. But edge deletion does not always imply the same. In fact, $E_m\left(G\right)$ may increase or decrease if an edge is deleted from a semigraph. In the example given below, one edge deletion decreases $E_m\left(G\right)$, while when the other edge is deleted $E_m\left(G\right)$ increases.

Example 5

Consider the semigraph $G=K_8^5$ with the vertex set $V\left(G\right)=1,2,3$, $4,5,6,7,8$ and the edge set $X\left(G\right)=(1,2,3,4,5),(1,6),(2,6),(3,6),(4$, $6),(5,6),(1,7),(2,7),(3,7),(4,7),(5,7),(1,8),(2,8),(3,8),(4,8),(5,8),(6,7),(6,8),(7,8)$. The adjacency matrix of $K_8^5$ is

Clearly the energy of $E_m\left(G\right)=17.37831$.

If we delete any edge joining a vertex of a semigraphical edge $(1,2$, $3,4,5)$ and any of the vertices $6,7,8$, the energy $E_m\left(G\right)$ increases. Whereas if any edge between the vertices $6,7,8$ or a partial/full edge $(1,2,3,4,5)$ is deleted then the energy $E_m\left(G\right)$ decreases.

The following are some examples where energy increases. $E_m(G-(1,6))=E_m(G-(5,6))=17.841059,E_m(G-(2,6))=17.939753$, $E_m(G-(3,6))=17.981907,E_m(G-(4,6))=17.939794$.

If we delete any of the edges $(4,5),(6,7),(8,7),E_m\left(G\right)$ decreases. $E_m(G-(4,5))=15.6333,E_m(G-(6,7))=16.67771,E_m(G-(8,7))=16.67771$.

Now we find some partial semigraphs of a given semigraph $G$ such that matrix energy of partial semigraph is necessarily less than or equal to the matrix energy of $G$. If $B$ is a principal submatrix of a square matrix $A$, then $E_m\left(B\right)\le E_m\left(A\right)$ (see [14]). However not all the principal submatrices of $A\left(G\right)$ are semigraphical. Also, every partial semigraph of $G$ does not have adjacency matrix which is a principal submatrix of $A\left(G\right)$.

Definition 5

Let $X_1$ be a nonempty subset of the edges of a semigraph $G(V,X)$ and $V_1$ be the set of the vertices belonging to the edges in $X_1$. The semigraph $G_1$ with vertex set $V_1$ and edge set $X_1$ is called the edge induced partial semigraph of $G$, induced by $X_1$. Further, this edge induced partial semigraph of $G$, induced by $X_1$, is called the edge induced complete semigraph if every edge containing two or more vertices of $V_1$ is in $X_1$.

Example 6

Consider a semigraph $G=(V,X)$ with $V=1,2,\dots ,8$, $X=e_1(1,2,3,4),e_2(4,5),e_3(1,6,5),e_4(4,6,7),e_5(5,7),e_6(2,6),e_7(5,8)$. A semigraph $G_1(V_1,X_1)$ with $V_1=1,5,6,8$ and $X_1=e_3(1,6,5),e_7(5,8)$ is an edge induced complete semigraph of the semigraph $G$. But $G_2(V_2,X_2)$ with $V_2=4,5,7$, $X_2=e_2(4,5),e_5(5,7)$ is not an edge induced complete semigraph of $G$, as $G$ contains the edge $e_4(4,6,7)$ but $G_2$ does not contain $e_4$ even though the vertices $4,7\in V_2$.

Definition 6

Let $X_1$ be a subset of $X$. Edge induced complete closure of $X_1$ is the smallest subset $Y$ of $X$ containing $X_1$ such that the edge induced partial semigraph of $Y$ is an edge induced complete semigraph.

Edge induced complete closure of $X_1$ is denoted by $\overline{X_1}$.

Algorithm to find edge induced complete closure:

Algorithm 1

Given: A nonempty subset $X_1$ of (full) edges of a semigraph $G$, to find $\overline{X_1}$.

1.	If $X_1=e$, then $\overline{X_1}=X_1$.

2.	If $X_1\ge 2$, then let $m_0=X_1,V_0=$ set of vertices on the edges of $m_0$. If $u,v\in V_0$ such that $u,v$ belong to an edge $e\in X$ and $e\notin m_0$, then add $e$ to $m_0$. $m_1=m_0\cup e\in X:\exists u,v\in V_0$ such that u,v are vertices of e and $e\notin m_0$.

3.	In general $m_{i+1}=m_i\cup e\in X:\exists u,v\in V_i$ such that $u,v$ belong to $e$ and $e\notin m_i$ and $V_{i+1}=$ set of vertices on the edges of $m_{i+1}$. If $m_{i+1}=m_i$ then $m_{i+1}=\overline{m_0}$.

4.	As $G$ has finitely many edges, the above process halts. □

Lemma 5

If $G_1$ is an edge induced complete semigraph of $G$, then $A\left(G_1\right)$ is a principal submatrix of $A\left(G\right)$.

Proof

Proof is clear from the definition of edge induced complete semigraph. □

Theorem 9

If $G_1$ is an edge induced complete semigraph of $G$, then $E_m\left(G_1\right)\le E_m\left(G\right)$.

Proof

The proof follows from Lemma 5. □

The above condition is sufficient, but not necessary for a partial semigraph $G_1$ of $G$ to have energy $E_m\left(G_1\right)\le E_m\left(G\right)$.

Example 7

Consider the semigraph $G$ with $V=1,2,3,4,5,6,7,8$, $X=e_1(8,7,2,6),e_2(1,2,3,4),e_3(3,7),e_4(2,5),e_5(6,5)$. The adjacency matrix of $G$ is

$E_m\left(G\right)=18.046392$.

Consider the edge induced partial semigraph $G_1=〈e_1,e_2〉$ of $G$ with $E_m\left(G_1\right)=14.716249$. Here $G_1$ is not an edge induced complete semigraph of $G$ and $E_m\left(G_1\right)\le E_m\left(G\right)$.

Notes

Peer review under responsibility of Kalasalingam University.