Some classes of trees with maximum number of holes two

Abstract

An $L\left(2,1\right)$-coloring of a simple connected graph $G$ is an assignment of non-negative integers to the vertices of $G$ such that adjacent vertices color difference is at least two, and vertices that are at distance two from each other get different colors. The maximum color assigned in an $L\left(2,1\right)$-coloring is called span of that coloring. The span of a graph $G$ denoted by $\lambda \left(G\right)$ is the smallest span taken over all $L\left(2,1\right)$-colorings of $G$. A hole is an unused color within the range of colors used by the coloring. An $L\left(2,1\right)$-coloring $f$ is said to be irreducible if no other $L\left(2,1\right)$-coloring can be produced by decreasing a color of $f$. The maximum number of holes of a graph $G$, denoted by $H_{\lambda }\left(G\right)$, is the maximum number of holes taken over all irreducible $L\left(2,1\right)$-colorings with span $\lambda \left(G\right)$. Laskar and Eyabi (Christpher, 2009) conjectured that if $T$ is a tree, then $H_{\lambda }\left(T\right)=2$ if and only if $T=P_n$, $n>4$. We show that this conjecture does not hold by providing a counterexample. Also, we give some classes of trees with maximum number of holes two.

Keywords:

• $L\left(2,1\right)$-coloring
• Span of a graph
• Irreducible coloring
• Maximum number of holes

1 Introduction

The Channel assignment problem is the problem of assigning frequencies to transmitters without interference. One of the variations of Channel assignment problem is $L\left(2,1\right)$-coloring of graphs. An $L\left(2,1\right)$-coloring of a graph $G$, introduced by Griggs and Yeh [1] is an assignment $f$ from the vertex set of $G$ to $\{0,1,2,\dots ,k\}$ such that $|f\left(u\right)-f\left(v\right)|⩾2$ if $d(u,v)=1$, and $|f\left(u\right)-f\left(v\right)|⩾1$ if $d(u,v)=2$, where $d(u,v)$ denotes the distance between the vertices $u$ and $v$. The span of $f$ is the largest integer assigned by $f$. The $L\left(2,1\right)$-span or span $\lambda \left(G\right)$ of a graph $G$ is the smallest span of $f$ taken over all $L\left(2,1\right)$-colorings of $G$. In the introductory paper, they have proved that $\lambda \left(P_n\right)=4$ for $n⩾5$ and they have shown that $\lambda \left(T\right)$ is either $\Delta +1$ or $\Delta +2$ for any tree $T$ with maximum degree $\Delta$. We refer a tree is Type-I if $\lambda \left(T\right)=\Delta +1$, otherwise Type-II. In a graph $G$ with maximum degree $\Delta$, we refer a vertex $v$ as a major vertex if its degree is $\Delta$, otherwise it is a minor vertex. A $\Delta$-path segment is a path between two major vertices. Wang [2] has proved that if a tree $T$ does not contain $\Delta$-path segments of length 1, 2 and 4, then $T$ is Type-I. Zhai et al. [3] improved the above condition as if $T$ does not contains $\Delta$-path segment of length 2 and 4, then $\lambda \left(T\right)=\Delta +1$. Mandal and Panigrahi [4] have found that $\lambda \left(T\right)=\Delta +1$ if $T$ has at most one $\Delta$-path segment of length either 2 or 4 and all other $\Delta$-path segments are of length at least 7. Wood and Jacob [5] have given a complete characterization of the $L(2,1)$-span of trees up to twenty vertices. Fishburn et al. [6] have introduced the concept of irreducibility of $L(2,1)$-coloring. An $L(2,1)$-coloring $f$ of a graph $G$ is said to be irreducible if there is no $L(2,1)$-coloring $g$ of $G$ such that $g\left(v\right)⩽f\left(v\right)$ for all vertices $v$ in $G$ and $g\left(u\right)<f\left(u\right)$ for at least one vertex $u$ of $G$. An integer $l$ between 0 and the span of an $L\left(2,1\right)$-coloring $f$ is said to be a hole if there is no vertex $v$ such that $f\left(v\right)=l$. The maximum number of holes over all irreducible span colorings of a graph $G$ is denoted by $H_{\lambda }\left(G\right)$. Laskar and Eyabi [7] have determined the maximum number of holes for paths, cycles, stars and complete bipartite graphs as 2, 2, 1 and 1 respectively. Also, they showed that $H_{\lambda }\left(T\right)\le 1$ for any Type-I tree $T$ and $H_{\lambda }\left(T\right)\le 2$ if $T$ is Type-II tree. Further, they conjectured as below.

Fig. 2.1. Irreducible L (2, 1)-span coloring of T₁ with two holes.

Conjecture 1.1

[7] For any tree $T$, $H_{\lambda }\left(T\right)=2$ if and only if $T$ is a path $P_n$, $n>4$.

In this paper, we give a counterexample for Conjecture 1.1 by giving a two hole irreducible span coloring for a Type-II tree which is not a path. Also, we consider some Type-II trees given by Wood and Jacob [5] and for each tree, we construct infinitely many Type-II trees with maximum number of holes two.

2 Counterexample

In this section, we give a counterexample to Conjecture 1.1. Wood and Jacob [5] have proved that a tree $T$ with maximum degree $\Delta =3$ and containing a subtree $T_1$ with four major vertices $v_1,v_2,v_3$ and $v_4$ of $T$ such that $v_1{v}_2$, $v_3{v}_4\in E\left(T\right)$, $d\left(v_2,v_3\right)=4$ and $d\left(v_1,v_4\right)=6$ is Type-II. For this subtree $T_1$, we define an irreducible span coloring with two holes which disproves Conjecture 1.1. For the sake of completeness, we give the proof given by Wood and Jacob [5] to show $T$ is Type-II.

Theorem 2.1

[5] A tree $T$ with maximum degree $\Delta =3$ and containing a subtree $T_1$ as below, is Type-II.

Proof

Suppose $T_1$ is Type-I, that is $\lambda \left(T_1\right)=4$. Let $f$ be a span coloring of $T_1$. In any span coloring of a Type-I tree, any major vertex receives either 0 or $\Delta +1$. Without loss of generality, let $f\left(v_1\right)=4$ and $f\left(v_2\right)=0$. If $f\left(v_3\right)=4$ and $f\left(v_4\right)=0$, then there is no possibility for coloring the vertices between $v_2$ and $v_3$. Suppose that $f\left(v_3\right)=0$ and $f\left(v_4\right)=4$. Since $f\left(v_1\right)=4$, $f\left(v_2\right)=0$ and $f\left(v_3\right)=0$, the only possibility for coloring the vertices between $v_2$ and $v_3$ is $〈314〉$. which is not possible as $f\left(v_4\right)=4$. Therefore $T_1$ is Type-II and hence $T$. $■$

The following example gives a counterexample for Conjecture 1.1.

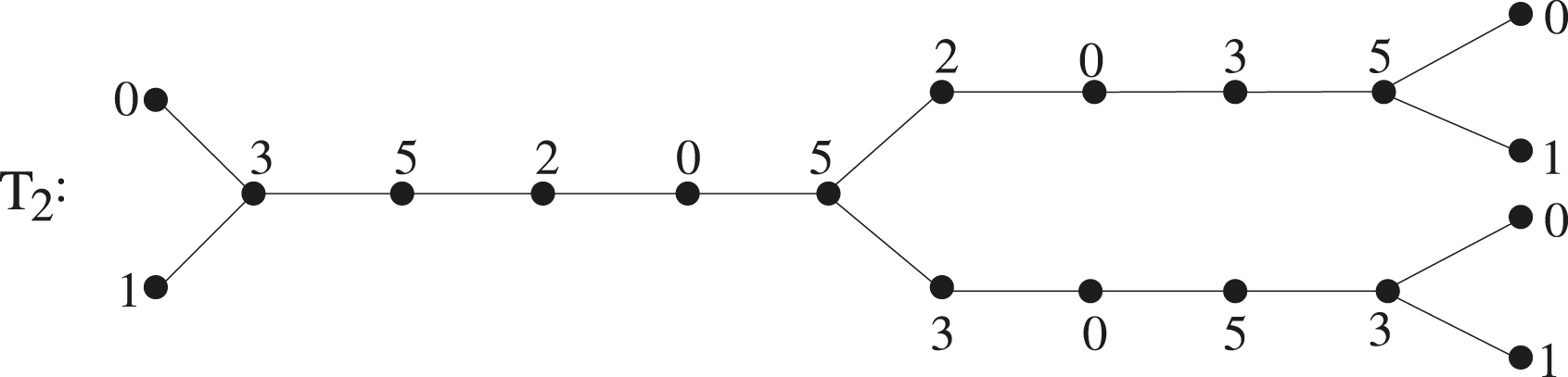
Example 2.2

It is clear that the coloring of $T_1$ given in Fig. 2.1 is an irreducible $L\left(2,1\right)$-span coloring with two holes.

3 Some classes of Type-II trees with maximum number of holes two

Wood and Jacob [5] have given some sufficient conditions for a tree to be Type-II. We consider some of their sufficient conditions as below.

Theorem 3.1

[5] A tree $T$ with maximum degree $\Delta$ and containing any of the following subtrees is Type-II.

1.	$\Delta =3,$
2.	$\Delta =3,$
3.	$\Delta =3,$
4.	$\Delta =3,$
5.	$\Delta =4,$

Now, we show that $H_{\lambda }\left(T_i\right)=1$, $2⩽i⩽6$. Later, in this section, we construct some classes of Type-II trees from $T_i$, $2⩽i⩽6$ with maximum number of holes two. In the following theorem, we prove that there is no irreducible $L\left(2,1\right)$-span coloring with two holes for $T_i$, $2⩽i⩽6$.

Theorem 3.2

For the trees $T_i$, $2⩽i⩽6$, $H_{\lambda }\left(T_i\right)⩽1$.

Proof

First, we consider $T_2$ with the following labeling and prove $H_{\lambda }\left(T_2\right)⩽1$.

Suppose that $T_2$ has an irreducible $L\left(2,1\right)$-span coloring $f$ with two holes $h$, $h^{\prime }$. Since 0, the span of $f$ and any two consecutive colors cannot be holes, the possibilities for $\{h,h^{\prime }\}$ are $\{1,3\}$, $\{1,4\}$ and $\{2,4\}$. If $\{h,h^{\prime }\}=\{1,3\}$, then any major vertex receives only either 0 or 2. If $f\left(v_1\right)=0$, then neighbors of $v_1$ receives 2, 4 and 5. Since at least one of the pendant vertices $u_1$ and $u_2$ receives the color 4 or 5 which is reducible to 3, $f\left(v_1\right)\ne 0$. So, $f\left(v_1\right)$, $f\left(v_3\right)$ and $f\left(v_4\right)$ must be 2. If $f\left(w_1\right)=0$, then $f\left(w_3\right)$ and $f\left(v_2\right)$ must be 2 and 0 respectively (as $f\left(w_2\right)$ is either 4 or 5). With this partial coloring there is no possibility for coloring the path $w_4{w}_5{w}_6$ (only two colors 4 and 5 are available). If $f\left(w_1\right)$ is either 4 or 5. Then $f\left(w_2\right)$ and $f\left(v_2\right)$ must be 0 and 2 respectively. Since either $w_4$ or $w_7$ receives 0, there is no possible coloring for either $w_5{w}_6$ or $w_8{w}_9$. Therefore, there is no irreducible span coloring of $T_2$ with holes 1 and 3.

If $\{h,h^{\prime }\}=\{1,4\}$, then any major vertex receives only 0 or 5. If $f\left(v_1\right)=5$, then one of the colors assigned to $u_1$ or $u_2$ reduces to 1. So, $f\left(v_1\right)$, $f\left(v_3\right)$ and $f\left(v_4\right)$ must be 0. If $u_1$ or $u_2$ receives 5 then it reduces to a hole 4. Therefore $u_1$ and $u_2$ receive the colors 2 and 3, and $w_1$ receives the color $5$. Since $f\left(w_1\right)=5$ and $f\left(w_2\right)=2$ or 3, $w_3$ and $v_2$ receive 0 and 5 respectively. With this partial coloring there is no possibility for coloring the path $w_4{w}_5{w}_6$ (only two colors 2 and 3 are available). Therefore, there is no irreducible span coloring of $T_2$ with 1 and 4 as holes.

If $\{h,h^{\prime }\}=\{2,4\}$, then any major vertex receives only 3 or 5. If $f\left(v_1\right)=3$ and $f\left(w_1\right)$ is 0 or 1, then $f\left(w_2\right)=5$ and $f\left(v_2\right)=3$. In this case color 5 received by $w_2$ reduces to a hole 4. If $f\left(v_1\right)=3$ and $f\left(w_1\right)=5$, then $f\left(w_3\right)$ and $f\left(v_2\right)$ must be 3 and 5 respectively. With this partial coloring the possibilities for coloring the path $w_4{w}_5{w}_6{v}_3$ are $〈0315〉$ and $〈1305〉$. In both the cases, one of the pendant vertices $u_3$ or $u_4$ receives 3, which reduces to a hole 2. If $f\left(v_1\right)=5$, then $f\left(w_1\right)$ must be $3$ otherwise $u_1$ or $u_2$ receives 3 which reduces to a hole $2$. So, $f\left(w_3\right)$ and $f\left(v_2\right)$ must be 5 and 3 respectively. With this partial coloring the possibilities for coloring the path $w_4{w}_5{w}_6$ are $〈051〉$ and $〈150〉$. In both the cases, the color 5 reduces to a hole 4. Therefore $H_{\lambda }\left(T_2\right)⩽1$.

Now, we consider $T_3$ with labeling as below.

Suppose that $T_3$ has an irreducible $L\left(2,1\right)$-span coloring $f$ with two holes $h$, $h^{\prime }$. The possibilities for $\{h,h^{\prime }\}$ are $\{1,3\}$, $\{1,4\}$ and $\{2,4\}$. If $\{h,h^{\prime }\}=\{1,3\}$, then as in $T_2$, $f\left(v_1\right)$, $f\left(v_3\right)$ and $f\left(v_4\right)$ must be 2. Since $v_2$ is adjacent to $v_3$, $f\left(v_2\right)=0$. With this partial coloring there is no possibility for coloring the path $w_1{w}_2{w}_3$. If $\{h,h^{\prime }\}=\{1,4\}$, then $f\left(v_1\right)$, $f\left(v_3\right)$ and $f\left(v_4\right)$ must be 0. As $v_2$ and $v_3$ are adjacent, $v_2$ receives $5$. With this partial coloring there is no possibility for coloring the path $w_1{w}_2{w}_3$. If $\{h,h^{\prime }\}=\{2,4\}$, then any major vertex receives only 3 or 5. If $f\left(v_3\right)=3$ and $f\left(v_2\right)=5$, the possibilities for coloring the path $v_1{w}_1{w}_2{w}_3$ are $〈5031〉$ and $〈5130〉$. In both the cases, $u_1$ or $u_3$ receives 3 which reduces to 2. If $f\left(v_3\right)=5$ and $f\left(v_2\right)=3$, then the possibilities to color the path $w_1{w}_2{w}_3$ are $〈051〉$ and $〈150〉$. In both the cases, the color 5 reduces to a hole 4. Therefore, there is no irreducible $L\left(2,1\right)$-span coloring for $T_3$ with two holes.

Next, we consider $T_4$ along with the following labeling.

Suppose that $T_4$ has an irreducible $L\left(2,1\right)$-span coloring $f$ with two holes $h$, $h^{\prime }$. Then $\{h,h^{\prime }\}$ is $\{1,3\}$ or $\{1,4\}$ or $\{2,4\}$. If $\{h,h^{\prime }\}=\{1,3\}$, then any major vertex receives only either 0 or 2. Since one of the vertices $v_1$ or $v_2$ must receive 0, a pendant vertex adjacent to it receives 4 or 5 which reduces to a hole 3. If $\{h,h^{\prime }\}=\{1,4\}$, then any major vertex receives only either 0 or 5. Since one of the vertices $v_1$ or $v_2$ must receive 5, a pendant vertex adjacent to it receives 2 or 3 which reduces to a hole 1. If $\{h,h^{\prime }\}=\{2,4\}$, then any major vertex receives only 3 or 5. If $f\left(v_1\right)=3$ and $f\left(v_2\right)=5$, then $f\left(w_2\right)=3$ which implies $f\left(v_3\right)=5$. Since the coloring is irreducible, $f\left(u_4\right)$ cannot be 3. With this partial coloring, there is no possibility for coloring the path $w_4{w}_5{w}_6$. If $f\left(v_1\right)=5$ and $f\left(v_2\right)=3$ then $f\left(w_2\right)=5$ which reduces to 4. Therefore $H_{\lambda }\left(T_4\right)⩽1$.

Now, consider $T_5$ with labeling as below.

Suppose that $T_5$ has an irreducible $L\left(2,1\right)$-span coloring $f$ with two holes $h$, $h^{\prime }$. The possibilities for $\{h,h^{\prime }\}$ are $\{1,3\}$, $\{1,4\}$ and $\{2,4\}$. If $\{h,h^{\prime }\}=\{1,3\}$, then as in $T_2$, $f\left(v_1\right)$, $f\left(v_3\right)$ and $f\left(v_5\right)$ must be 2, and $f\left(v_2\right)=f\left(v_4\right)=0$. With this partial coloring there is no possibility for coloring the path $w_2{w}_3{w}_4{w}_5$. If $\{h,h^{\prime }\}=\{1,4\}$, then as in $T_2$, $f\left(v_1\right)$, $f\left(v_3\right)$ and $f\left(v_5\right)$ must be 0. Then one of the pendant vertices $u_1$ and $u_2$ receives the color 5 which is reducible to 4. If $\{h,h^{\prime }\}=\{2,4\}$, then any major vertex receives only 3 or 5. If $v_1$ receives 5, then $f\left(v_2\right)=3$ and one of the pendant vertices $u_1$ and $u_2$ receives the color 3 which is reducible to 2. Therefore $f\left(v_1\right)$ and $f\left(v_5\right)$ must be 3 and hence $f\left(v_2\right)=5$, $f\left(v_3\right)=3$ and $f\left(v_4\right)=5$. With this partial coloring there is no possibility to color the path $w_2{w}_3{w}_4{w}_5$. Therefore $H_{\lambda }\left(T_5\right)⩽1$.

Finally, we consider the tree $T_6$ along with labeling as below.

Suppose $T_6$ has an irreducible $L\left(2,1\right)$-span coloring $f$ with holes $h$, $h^{\prime }$. The possibilities for $\{h,h^{\prime }\}$ are $\{1,3\}$, $\{1,5\}$ and $\{3,5\}$. If $\{h,h^{\prime }\}=\{1,3\}$, then any major vertex receives 0 or 2 only. Without loss of generality, we assume $f\left(v_1\right)=0$ and $f\left(v_2\right)=2$. Then one of the pendant vertices adjacent to $v_1$ must receive 4 which reduces to 3. Similarly one can see that other two cases are not possible. Therefore $H_{\lambda }\left(T_6\right)⩽1$. $■$

Theorem 3.3

For the trees $T_i$, $2⩽i⩽6$, $H_{\lambda }\left(T_i\right)=1$.

Proof

From Theorem 3.2, we have $H_{\lambda }\left(T_i\right)⩽1$, $2⩽i⩽6$. It is easy to see that the colorings of $T_i$, $2⩽i⩽6$ given below are irreducible $L\left(2,1\right)$-span colorings with one hole. Therefore $H_{\lambda }\left(T_i\right)=1$, $2⩽i⩽6$.

$■$

3.1 Construction of Type-II trees with maximum number of holes two

We start this subsection with a lemma that gives a Type-II tree with maximum number of holes two from a Type-II tree with a two hole $L\left(2,1\right)$-span coloring without changing the span. Later, we apply this lemma on trees $T_i$, $1⩽i⩽6$ to construct infinitely many trees with maximum number of holes two.

Lemma 3.4

If $T$ is a Type-II tree and $T$ has a two hole reducible span coloring, then there exists a tree $T^{\prime }$ such that $T$ is a subtree of $T^{\prime }$, $\lambda \left(T^{\prime }\right)=\lambda \left(T\right)$ and $H_{\lambda }\left(T^{\prime }\right)=2$.

Proof

Let $T$ be a Type-II tree with maximum degree $\Delta$ and let $f$ be a reducible $L\left(2,1\right)$-span coloring of $T$ with two holes $h$ and $h^{\prime }$. Without loss of generality $h<h^{\prime }$. Now, we give a procedure to construct $T^{\prime }$ from $T$.

Step-I: Whenever a vertex color reduction is possible to a color other than hole, we reduce the color. Finally, $f$ is an $L\left(2,1\right)$-span coloring of $T$ with no vertex color can be reduced to a color other than hole.

Step-II: Suppose that a color received by a minor vertex $u$ reduces to $h^{\prime }$. Let $k$ be the order of the set $S_u=\{c:0⩽c<h^{\prime },c\ne h\text{and c is not the color assigned to any}$ $\text{neighbor of u}\}$. Now we attach $k$ new pendant vertices and we assign them the $k$ colors from $S_u$. Apply this procedure to all the minor vertices whose color reduces to $h^{\prime }$.

Step-III: We follow the procedure of Step-II for all the minor vertices in the tree obtained from Step-II by replacing $h^{\prime }$ by $h$. Let $T^{\prime }$ obtained finally.

Next, we show that the coloring of $T^{\prime }$ is an irreducible span coloring. From Step-I, Step-II and Step-III, it is clear that none of the minor vertex colors is reducible. Now, we prove that any major vertex color is not reducible to a hole. Suppose that a color $l$ assigned to a major vertex $u$ reduces to a hole $l^{\prime }$. It is clear that $l\ne 0,1$. If $2⩽l⩽\Delta +1$, then none of the colors $l^{\prime }-1$, $l^{\prime }$, $l^{\prime }+1$, $l-1$, $l$ and $l+1$ can be given to the neighbors of $u$. Since in any case the colors $l^{\prime }-1$, $l^{\prime }$, $l^{\prime }+1$, $l-1$, $l$ and $l+1$ are at least 4, it is not possible to color the $\Delta$ neighbors of $u$. If $l=\Delta +2$, then $l^{\prime }<\Delta +1$ is not possible as above. So, $l=\Delta +2$ and $l^{\prime }=\Delta +1$. Since $0,1,2,\dots ,\Delta -1$ are used to color the $\Delta$ neighbors of $u$, the other hole must be $\Delta$ which is not possible as $\Delta$ and $\Delta +1$ are consecutive. $■$

Theorem 3.5

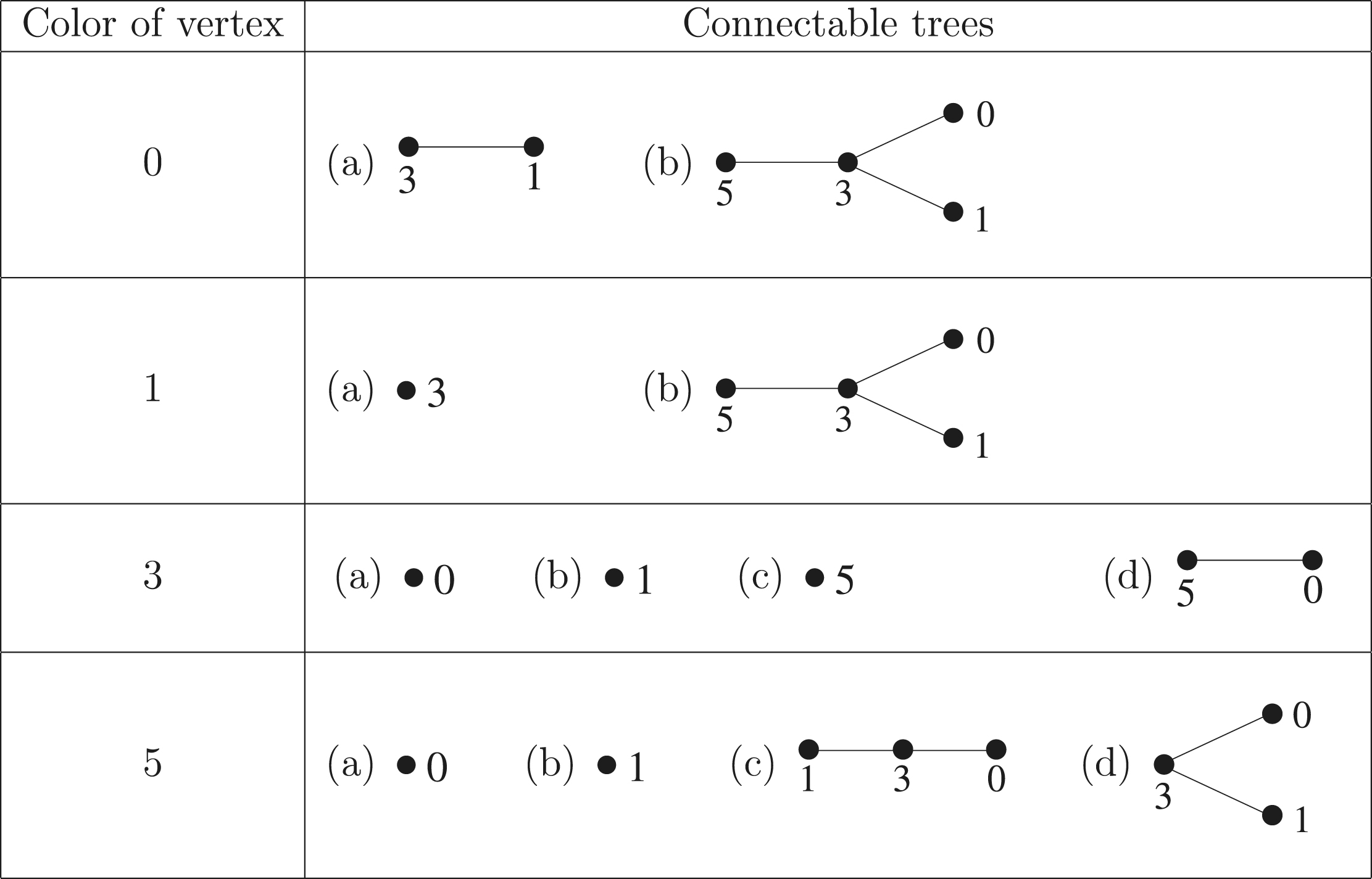
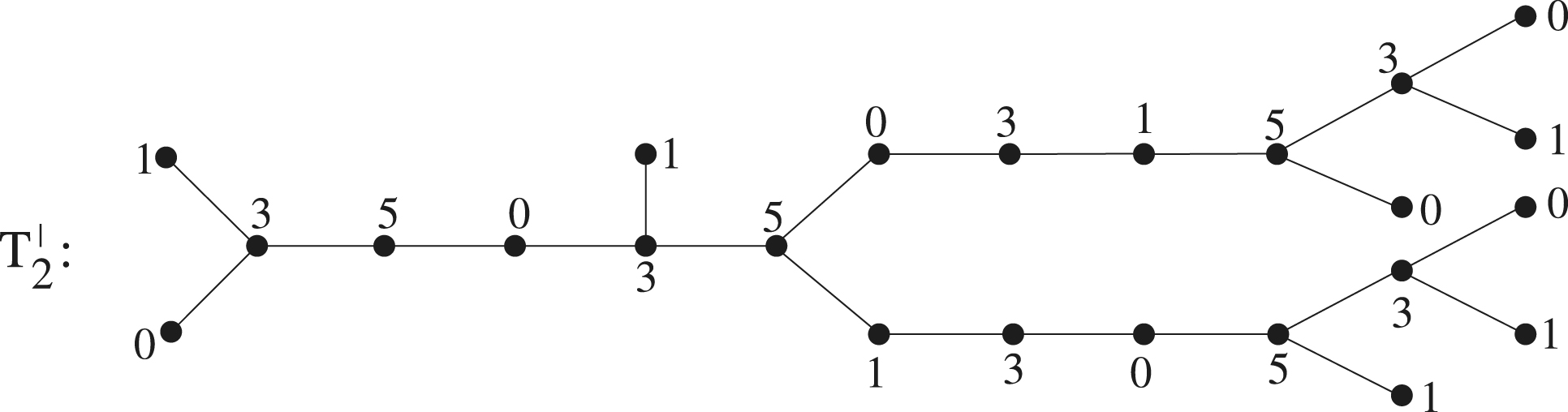
There are infinitely many Type-II trees with $\Delta =3$ and maximum number of holes two.

Proof

Since the trees $T_i$, $2⩽i⩽5$ have reducible $L\left(2,1\right)$-span colorings with two holes, we apply Lemma 3.4 and get the following trees $T_i^{\prime }$, $2⩽i⩽5$ with irreducible span colorings $f_i$, $2⩽i⩽5$ with two holes.

Let $f_1$ be the irreducible $L\left(2,1\right)$-span coloring of $T_1$ given in Example 2.2 and let $T_1^{\prime }=T_1$. Now, we construct infinitely many Type-II trees with $\Delta =3$ and maximum number of holes two from $T_i^{\prime }$, $1⩽i⩽5$. When we say connecting two trees, we mean adding an edge between them. Let $c$ be a color of a vertex $u$ in $T_i^{\prime }$, $1⩽i⩽5$. Depending on the colors of neighbors of $u$, we connect the trees (one at a time) given in Table 3.1 corresponding to the color $c$ with the first vertex to $T_i^{\prime }$ at $u$. In the case of connecting a single vertex, first we connect the smallest colored vertex to maintain irreducibility. It is easy to see that after every step the tree obtained is Type-II with maximum number of holes two and $\Delta =3$. Also, since at every step, connecting of trees to the pendant vertices is possible, we get infinitely many trees. $■$

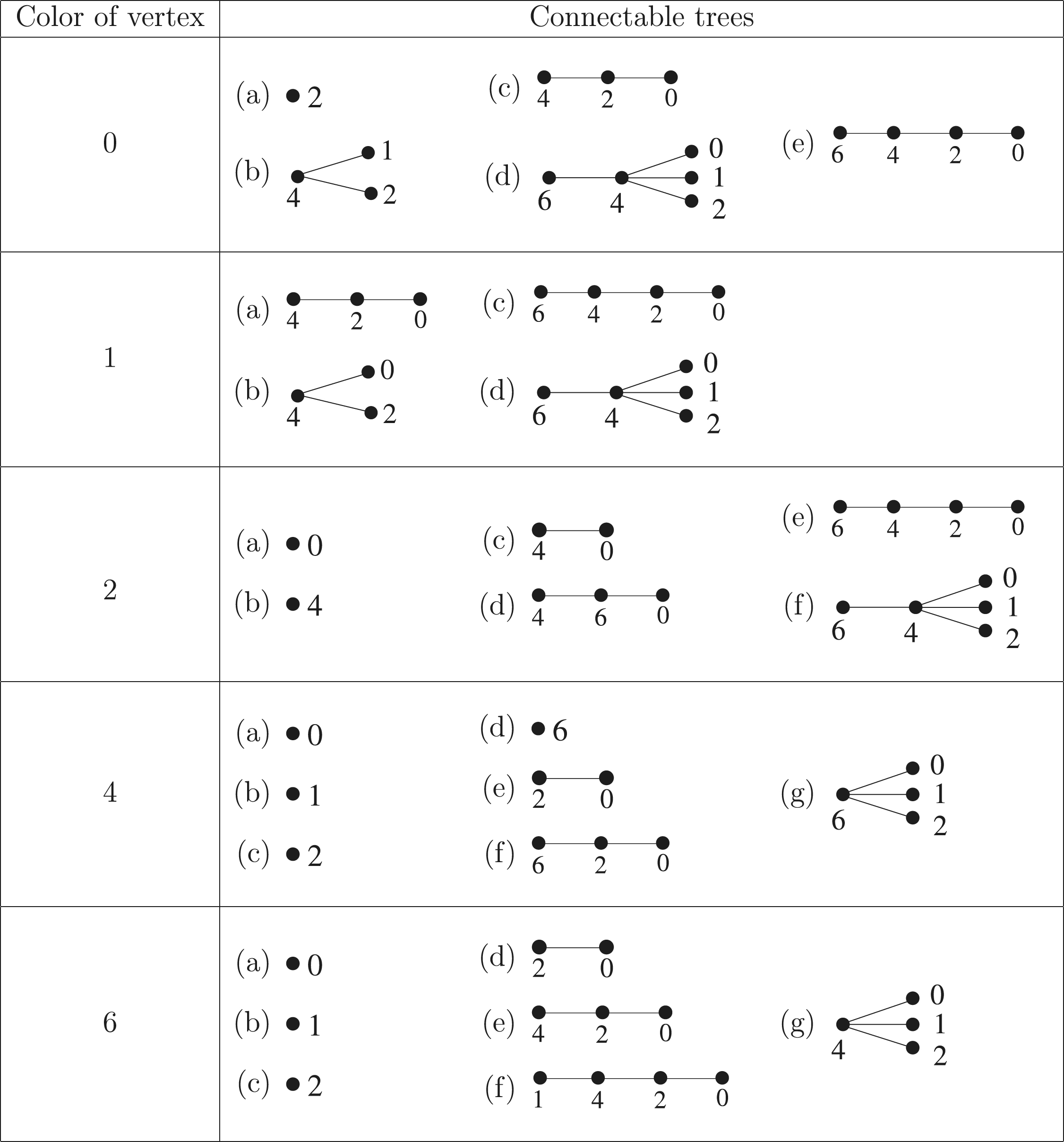
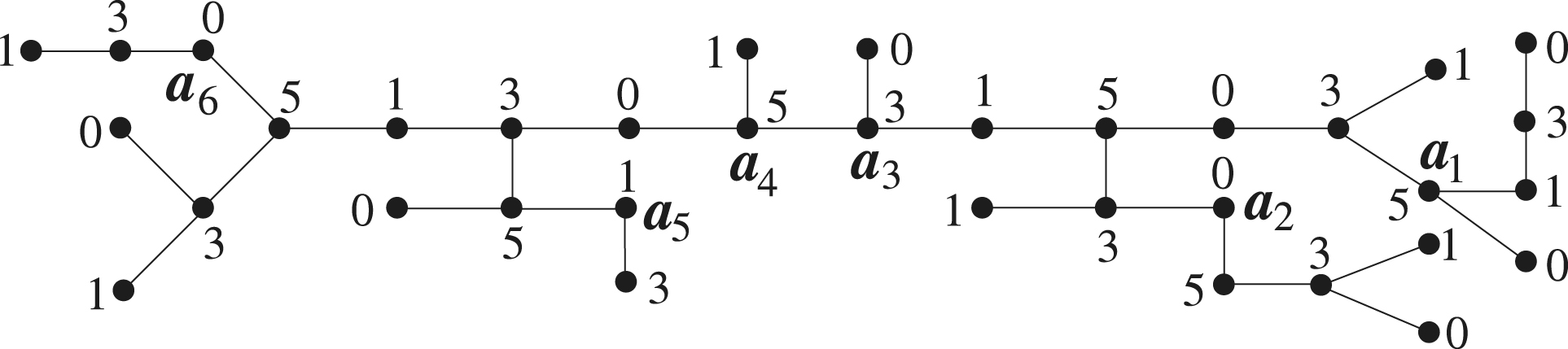
Example 3.6

In this example, we give an illustration of Theorem 3.5 for the tree $T_5^{\prime }$. The vertex $a_1$ has the color 5 and its neighbor’s color is 3 in $T_5^{\prime }$. From Theorem 3.5, there are only two possibilities (a) and (c) corresponding to color 5 in Table 3.1 out of which (a) is connected first. Later, out of the two possibilities, (b) and (c) for the vertex $a_1$, (c) is connected. Similarly, some trees are connected for the vertices $a_i$, $1⩽i⩽6$.

Theorem 3.7

There are infinitely many Type-II trees with $\Delta =4$ and maximum number of holes two.

Proof

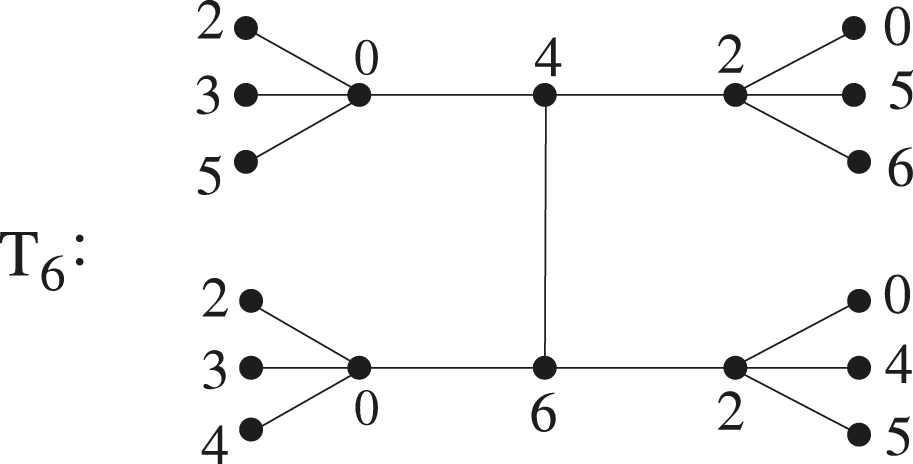
We apply Lemma 3.4 on $T_6$ to get figure $T_6^{\prime }$ with coloring f₆ as below. Rest of the proof is similar to that of Theorem 3.5 and using Table 3.2. $■$

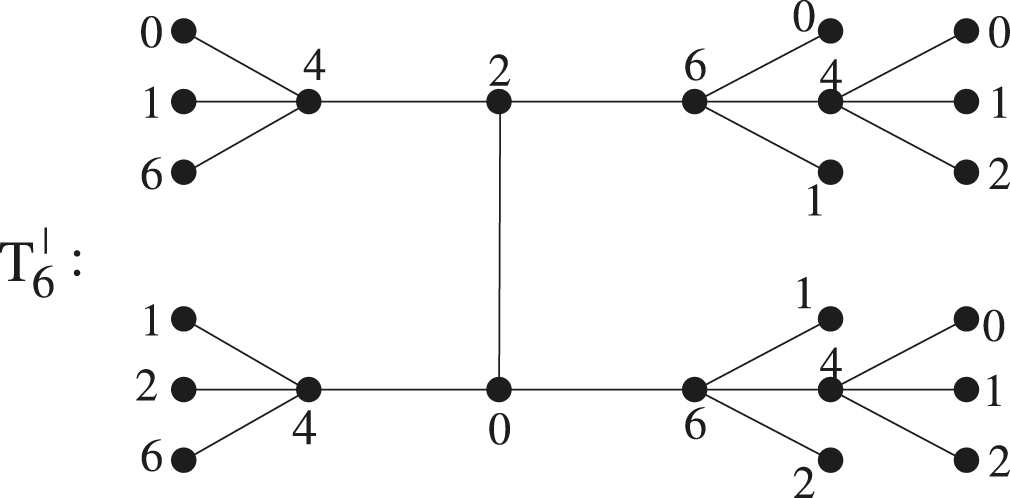
Remark

Tables 3.1 and 3.2 are obtained using the concept in the proof of Lemma 3.4. It is easy to see that connecting a tree (not a tree obtained by connecting some trees from the table) to $T_i^{\prime }$, $1⩽i⩽6$ other than the trees listed in the tables, produces a reducible L (2, 1)-span coloring for the resultant tree. Therefore, the class of trees generated from the tables is complete with respect to $f_i$, $1⩽i⩽6$. Changing two hole coloring of $T_i^{\prime }$, $1⩽i⩽6$ produces different class of Type-II trees with maximum number of holes two.