F index of graphs based on four new operations related to the strong product

Abstract

For a molecular graph, the first Zagreb index of a graph is equal to the sum of squares of the vertex degrees of the graph and the forgotten topological index (F-index) of a graph is defined as the sum of cubes of the vertex degrees of the graph. These parameters have applications in chemistry and drug structures. In this paper, we study the F index of strong product of two connected graphs in which one of the graphs is obtained by using four new sums called F sums of graphs and the other is any connected graph.

Keywords:

• F index
• Degree
• Subdivision of graph
• Total graph
• Strong product

1 Introduction

Throughout this paper we consider only simple connected graphs, that is, connected graphs without loops and multiple edges. For a graph $G=(V,E)$ with vertex set $V=V\left(G\right)$ and edge set $E=E\left(G\right)$, the degree of a vertex $v$ in $G$ is the number of edges incident to $v$ and is denoted by $d_G\left(v\right)$.

A graphical invariant is a number related to a graph which is structurally invariant. In chemical graph theory, these invariant numbers are also known as the topological indices. The first and second Zagreb indices of a graph are among the most studied vertex degree based topological indices. These indices were introduced by Gutman and Trinajestić [1], to study the structure dependency of the total $\pi$-electron energy on molecular structure, and this was elaborated on in [2]. Another vertex degree based topological index was defined in [1] where the Zagreb indices were introduced, and this index was not further studied until it was studied by Furtula and Gutman in the article [3]. A few basic properties of the forgotten topological index and the significant enhancement of physico-chemical applicability of the first Zagreb index are shown in [3].

Also forgotten topological index of several widely chemical structures which often appear in drug molecular graphs were presented in [4]. The lower and upper bounds of forgotten topological index in terms of graph irregularity, Zagreb indices, graph size and maximum/minimum vertex degrees were given in [5].

For a (molecular) graph $G$, the first Zagreb index $M_1\left(G\right)$ and the second Zagreb index $M_2\left(G\right)$ are, respectively, defined as follows: $$M_1=M_1\left(G\right)=\sum _{v\in V\left(G\right)}{d}_G^2\left(v\right),M_2=M_2\left(G\right)=\sum _{uv\in E\left(G\right)}{d}_G\left(u\right)d_G\left(v\right).$$Also, $M_1\left(G\right)={\sum }_{uv\in E\left(G\right)}[d_G\left(u\right)+d_G\left(v\right)]$. For more details on these indices see the recent papers [6–13] and the references therein. The zeroth-order general Randić index is a more general case of the first Zagreb index [14,15] and see survey paper on Randić index [16].

In [17], exact expressions for the first and second Zagreb indices of graph operations containing the Cartesian product, composition, join, disjunction, and symmetric difference of graphs were presented. Also, exact expressions for the first and second Zagreb indices of graphs based on operations related to the Cartesian product and the lexicographic product were given in [18] and [19], respectively. The closed formulas for the F-index of four operations of graphs to Cartesian product were determined in [20].

In this work, we will study the F index of four new operations related to the strong product on graphs. For this purpose, we recall some operations on graphs in the following (see also [17–21]).

The strong product of two connected graphs $G_1$ and $G_2$, which is denoted by $G_1\circ G_2$, is a graph such that the set of vertices is $V\left(G_1\right)\times V\left(G_2\right)$ and two vertices $u=(u_1,v_1)$ and $v=(u_2,v_2)$ are adjacent in $G_1\circ G_2$ if and only if, either (i) $u_1=u_2$ and $v_1$ is adjacent with $v_2$, or (ii) $u_1$ is adjacent with $u_2$ and $v_1=v_2$, or (iii) $u_1$ is adjacent with $u_2$ and $v_1$ is adjacent with $v_2$.

It is easy to see that $d_{G_1\circ G_2}(u_1,v_1)=d_{G_1}\left(u_1\right)+d_{G_2}\left(v_1\right)+d_{G_1}\left(u_1\right)d_{G_2}\left(v_1\right)$.

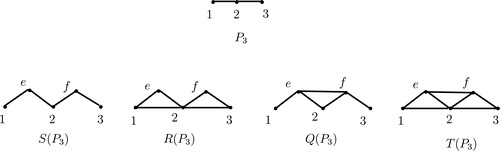
For a connected graph $G$, there are four related graphs as follows:

(a) $S\left(G\right)$ is the graph obtained by inserting an additional vertex in each edge of $G$. Equivalently, each edge of $G$ is replaced by a path of length 2.

(b) $R\left(G\right)$ is obtained from $G$ by adding a new vertex corresponding to each edge of $G$, then joining each new vertex to the end vertices of the corresponding edge.

(c) $Q\left(G\right)$ is obtained from $G$ by inserting a new vertex into each edge of $G$, then joining with edges those pairs of new vertices on adjacent edges of $G$.

(d) $T\left(G\right)$ has as its vertices the edges and vertices of $G$. Adjacency in $T\left(G\right)$ is defined as adjacency or incidence for the corresponding elements of $G$.

The graphs $S\left(G\right)$ and $T\left(G\right)$ are called the subdivision and total graph of $G$, respectively. For more details on these operations we refer the reader to [22]. The graphs $R\left(G\right)$ and $Q\left(G\right)$ are called the triangle parallel graph and the line superposition graph of $G$ in [23], respectively.

Note that (i) $R\left(G\right)$ can be obtained by replacing each edge of $G$ by a triangle, its vertex set is the union of $V\left(G\right)$ and $E\left(G\right)$, and its edge set is the union of the respective edge sets of $G$ and $S\left(G\right)$; (ii) $Q\left(G\right)$ is a graph on the same vertex set as $S\left(G\right)$ whose edge set is the union of the edge sets of $S\left(G\right)$ and the line graph $L\left(G\right)$ of $G$.

Yarahmadi et al. [23] presented explicit formulas expressing the eccentric connectivity indices of $S\left(G\right),R\left(G\right),Q\left(G\right),T\left(G\right)$ in terms of the eccentric connectivity index of the original graph $G$ and some auxiliary invariants.

If $G$ is $P_3$, then $S\left(P_3\right),R\left(P_3\right),Q\left(P_3\right)$ and $T\left(P_3\right)$ are shown in Fig. 1 (see [18,19]).

Fig. 1 $P_3,S\left(P_3\right),R\left(P_3\right),Q\left(P_3\right)andT\left(P_3\right)$.

Based on the Cartesian product $G_1\times G_2$ of two connected graphs $G_1$ and $G_2$ and the four types $S,R,Q,T$ of graphs resulting from edge subdivision above, M. Eliasi and B. Taeri [21] introduced four new operations on these graphs.

The expression for the Wiener index $W\left(G_1{+}_F{G}_2\right)$ of the $F$-sums of graph $G_1{+}_F{G}_2$ in terms of $W\left(F\left(G_1\right)\right)$ and $W\left(G_2\right)$ and the first and second Zagreb indices for the $F$-sums of graph were obtained in [21] and [18], respectively.

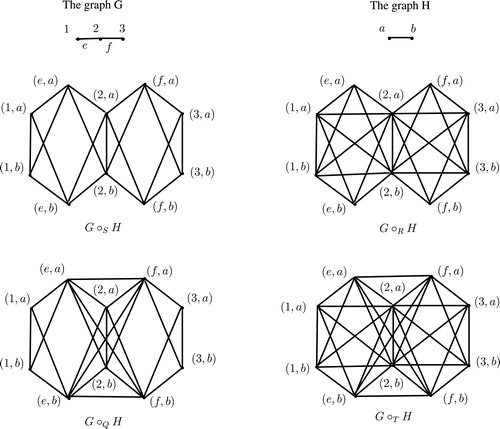
Also based on the strong product $G_1\circ G_2$ of two connected graphs $G_1$ and $G_2$ and the four types $S,R,Q,T$ of graphs resulting from edge subdivision, we also introduce four new operations on these graphs in the following:

Let $F\in \left\{S,R,Q,T\right\}$. The $F$-sum of $G_1$ and $G_2$, denoted by $G_1{\circ }_F{G}_2$, is defined by $F\left(G_1\right)\circ G_2-E^{\ast }$, where $E^{\ast }=\{(u,v_1)(u,v_2)\in E(F\left(G_1\right)\circ G_2):u\in V\left(F\left(G_1\right)\right)-V\left(G_1\right),v_1{v}_2\in E\left(G_2\right)\}$, i.e., $G_1{\circ }_F{G}_2$ is a graph with the set of vertices $V\left(G_1{\circ }_F{G}_2\right)=V\left(F\left(G_1\right)\right)\times V\left(G_2\right)=(V\left(G_1\right)\cup E\left(G_1\right))\times V\left(G_2\right)$ and two vertices $u=(u_1,v_1)$ and $v=(u_2,v_2)$ of $G_1{\circ }_F{G}_2$ are adjacent if and only if, either (i) $u_1=u_2\in V\left(G_1\right)$ and $v_1{v}_2\in E\left(G_2\right)$, or (ii) $u_1{u}_2\in E\left(F\left(G_1\right)\right)$ and $v_1=v_2\in V\left(G_2\right)$, or (iii) $u_1{u}_2\in E\left(F\left(G_1\right)\right)$ and $v_1{v}_2\in E\left(G_1\right)$.

For any vertex $(x,y)\in V\left(G_1{\circ }_F{G}_2\right)$, the degree of $(x,y)$ in the $F$-strong product $G_1{\circ }_F{G}_2$ is $$d(x,y)=\left\{\begin{array}{cc}{d}_{F\left(G_1\right)}\left(x\right)+d_{G_2}\left(y\right)+d_{F\left(G_1\right)}\left(x\right)d_{G_2}\left(y\right),\hfill & \text{if}x\in V\left(G_1\right);\hfill \\ d_{F\left(G_1\right)}\left(x\right)+d_{F\left(G_1\right)}\left(x\right)d_{G_2}\left(y\right),\hfill & \text{if}x\in V\left(F\left(G_1\right)\right)-V\left(G_1\right).\hfill \end{array}\right.$$ $P_3{\circ }_S{P}_2$, $P_3{\circ }_R{P}_2$, $P_3{\circ }_Q{P}_2$ and $P_3{\circ }_T{P}_2$ are shown in Fig. 2.

Fig. 2 Graphs $G$ and $H$ and $G{\circ }_{F}H$.

In this work, we will study the F index for the $F$-strong product of graphs.

2 The F index for $F$-strong product of graphs

Firstly, we will give the expression for the F index of $G_1{\circ }_S{G}_2$ in terms of F index and Zagreb indices of graphs $G_1$ and $G_2$.

Theorem 1

Let $G_i$ be a connected graph with $n_i$ vertices and $e_i$ edges, $i=\text{1,2}$. Then $$\begin{array}{cc}\hfill F\left(G_1{\circ }_S{G}_2\right)=& [n_2+3M_1\left(G_2\right)+6e_2]F\left(G_1\right)+[n_1+3M_1\left(G_1\right)+14e_1]F\left(G_2\right)\hfill \\ \hfill & +6e_2{M}_1\left(G_1\right)+30e_1{M}_1\left(G_2\right)+6M_1\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +F\left(G_1\right)F\left(G_2\right)+48e_1{e}_2+8n_2{e}_1.\hfill \end{array}$$

Proof

For any vertex $(x,y)\in V\left(G_1{\circ }_S{G}_2\right)$, the degree $d(x,y)$ of $(x,y)$ is $$\begin{array}{cc}\hfill d(x,y)=& \left\{\begin{array}{cc}{d}_{S\left(G_1\right)}\left(x\right)+d_{G_2}\left(y\right)+d_{S\left(G_1\right)}\left(x\right)d_{G_2}\left(y\right),\hfill & \text{if}x\in V\left(G_1\right);\hfill \\ d_{S\left(G_1\right)}\left(x\right)+d_{S\left(G_1\right)}\left(x\right)d_{G_2}\left(y\right),\hfill & \text{if}x\in V\left(S\left(G_1\right)\right)-V\left(G_1\right)\hfill \end{array}\right.\hfill \\ \hfill =& \left\{\begin{array}{cc}{d}_{G_1}\left(x\right)+d_{G_2}\left(y\right)+d_{G_1}\left(x\right)d_{G_2}\left(y\right),\hfill & \text{if}x\in V\left(G_1\right);\hfill \\ 2+2d_{G_2}\left(y\right),\hfill & \text{if}x\in V\left(S\left(G_1\right)\right)-V\left(G_1\right).\hfill \end{array}\right.\hfill \end{array}$$

For $v_1{v}_2\in E\left(G_2\right)$ and $u_1{u}_2\in E\left(S\left(G_1\right)\right)$, if $u_1\in V\left(G_1\right)$ and $u_2\in V\left(S\left(G_1\right)\right)-V\left(G_1\right)$, i.e., $u_2$ is a new vertex inserted on an edge incident to $u_1$, then $(u_1,v_1)(u_2,v_2)\in E\left(G_1{\circ }_S{G}_2\right)$ and $(u_1,v_2)(u_2,v_1)\in E\left(G_1{\circ }_S{G}_2\right)$. $$\begin{array}{cc}\hfill F\left(G_1{\circ }_S{G}_2\right)=& \sum _{(u_1,v_1)(u_2,v_2)\in E\left(G_1{\circ }_s{G}_2\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill =& \sum _{u_1=u_2\in V\left(G_1\right)}\sum _{v_1{v}_2\in E\left(G_2\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & +\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{u_1{u}_2\in E\left(S\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & +\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{u_1{u}_2\in E\left(S\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill =& \sum {}_1+\sum {}_2+\sum {}_3.\hfill \end{array}$$Then $$\begin{array}{cc}\hfill & \sum {}_1=\sum _{u_1=u_2\in V\left(G_1\right)}\sum _{v_1{v}_2\in E\left(G_2\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{u\in V\left(G_1\right)}\sum _{v_1{v}_2\in E\left(G_2\right)}[{(d\left(u\right)+d\left(v_1\right)+d\left(u\right)d\left(v_1\right))}^2+{(d\left(u\right)+d\left(v_2\right)+d\left(u\right)d\left(v_2\right))}^2]\hfill \\ \hfill & =\sum _{u\in V\left(G_1\right)}\sum _{v_1{v}_2\in E\left(G_2\right)}[2d^2\left(u\right)+d^2\left(v_1\right)+d^2\left(v_2\right)+d^2\left(u\right)(d^2\left(v_1\right)+d^2\left(v_2\right))\hfill \\ \hfill & +2d\left(u\right)(d\left(v_1\right)+d\left(v_2\right))+2d^2\left(u\right)(d\left(v_1\right)+d\left(v_2\right))+2d\left(u\right)(d^2\left(v_1\right)+d^2\left(v_2\right))]\hfill \\ \hfill & =\sum _{u\in V\left(G_1\right)}[e_2\left(2d^2\left(u\right)\right)+F\left(G_2\right)+d^2\left(u\right)F\left(G_2\right)+2d\left(u\right)M_1\left(G_2\right)\hfill \\ \hfill & +2d^2\left(u\right)M_1\left(G_2\right)+2d\left(u\right)F\left(G_2\right)]\hfill \\ \hfill & =2e_2{M}_1\left(G_1\right)+n_{1}F\left(G_2\right)+M_1\left(G_1\right)F\left(G_2\right)+2\left(2e_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +2M_1\left(G_1\right)M_1\left(G_2\right)+2\left(2e_1\right)F\left(G_2\right)\hfill \\ \hfill & =2e_2{M}_1\left(G_1\right)+n_{1}F\left(G_2\right)+M_1\left(G_1\right)F\left(G_2\right)+4e_1{M}_1\left(G_2\right)+2M_1\left(G_1\right)M_1\left(G_2\right)+4e_{1}F\left(G_2\right).\hfill \end{array}$$and $$\begin{array}{cc}\hfill & \sum {}_2=\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{u_1{u}_2\in E\left(S\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & (\text{Without loss of generality, we assume that}{u}_1\in V\left(G_1\right),u_2\in V\left(S\left(G_1\right)\right)-V\left(G_1\right).)\hfill \\ \hfill & =\sum _{v\in V\left(G_2\right)}\sum _{u_1{u}_2\in E\left(S\left(G_1\right)\right)}[{(d\left(u_1\right)+d\left(v\right)+d\left(u_1\right)d\left(v\right))}^2+{(d\left(u_2\right)+d\left(u_2\right)d\left(v\right))}^2]\hfill \\ \hfill & =\sum _{v\in V\left(G_2\right)}\sum _{u_1{u}_2\in E\left(S\left(G_1\right)\right)}[d^2\left(u_1\right)+d^2\left(u_2\right)+d^2\left(v\right)(d^2\left(u_1\right)+d^2\left(u_2\right))+2d\left(v\right)(d^2\left(u_1\right)\hfill \\ \hfill & +d^2\left(u_2\right))+2d\left(u_1\right)d\left(v\right)+2d\left(u_1\right)d^2\left(v\right)+d^2\left(v\right)]\hfill \\ \hfill & =\sum _{v\in V\left(G_2\right)}[F\left(S\left(G_1\right)\right)+d^2\left(v\right)F\left(S\left(G_1\right)\right)+2d\left(v\right)F\left(S\left(G_1\right)\right)\hfill \\ \hfill & +2d\left(v\right)M_1\left(G_1\right)+2d^2\left(v\right)M_1\left(G_1\right)+2e_1{d}^2\left(v\right)]\hfill \\ \hfill & =n_{2}F\left(S\left(G_1\right)\right)+M_1\left(G_2\right)F\left(S\left(G_1\right)\right)+4e_{2}F\left(S\left(G_1\right)\right)+4e_2{M}_1\left(G_1\right)\hfill \\ \hfill & +2M_1\left(G_1\right)M_1\left(G_2\right)+2e_1{M}_1\left(G_2\right).\hfill \end{array}$$

Note that $F\left(S\left(G_1\right)\right)=F\left(G_1\right)+8e_1$, we have $$\sum {}_2=[n_2+M_1\left(G_2\right)+4e_2]F\left(G_1\right)+2M_1\left(G_1\right)M_1\left(G_2\right)+10e_1{M}_1\left(G_2\right)+4e_2{M}_1\left(G_1\right)+8e_1(n_2+4e_2).$$ $$\begin{array}{cc}\hfill & \sum {}_3=\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{u_1{u}_2\in E\left(S\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(S\left(G_1\right)\right)u_1\in V\left(G_1\right),}{u_2\in V\left(S\left(G_1\right)\right)-V\left(G_1\right)}}[{(d\left(u_1\right)+d\left(v_1\right)+d\left(u_1\right)d\left(v_1\right))}^2+{(d\left(u_2\right)+d\left(u_2\right)d\left(v_2\right))}^2]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(S\left(G_1\right)\right)u_1\in V\left(G_1\right),}{u_2\in V\left(S\left(G_1\right)\right)-V\left(G_1\right)}}[d^2\left(u_1\right)+d^2\left(u_2\right)+d^2\left(v_1\right)+d^2\left(u_1\right)d^2\left(v_1\right)+2d\left(u_1\right)d\left(v_1\right)\hfill \\ \hfill & +2d^2\left(u_1\right)d\left(v_1\right)+2d\left(u_1\right)d^2\left(v_1\right)+d^2\left(u_2\right)d^2\left(v_2\right)+2d^2\left(u_2\right)d\left(v_2\right)]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(S\left(G_1\right)\right)u_1\in V\left(G_1\right),}{u_2\in V\left(S\left(G_1\right)\right)-V\left(G_1\right)}}[[d^2\left(u_1\right)+d^2\left(u_2\right)]+\left[d^2\left(v_1\right)\right]+\left[d^2\left(u_1\right)d^2\left(v_1\right)\right]\hfill \\ \hfill & +\left[2d\left(u_1\right)d\left(v_1\right)\right]+\left[2d^2\left(u_1\right)d\left(v_1\right)\right]+\left[2d\left(u_1\right)d^2\left(v_1\right)\right]+\left[d^2\left(u_2\right)d^2\left(v_2\right)\right]+\left[2d^2\left(u_2\right)d\left(v_2\right)\right]]\hfill \\ \hfill & =2e_{2}F\left(G_1\right)+16e_1{e}_2+2e_{1}F\left(G_2\right)+F\left(G_1\right)F\left(G_2\right)+2M_1\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +2F\left(G_1\right)M_1\left(G_2\right)+2M_1\left(G_1\right)F\left(G_2\right)+8e_{1}F\left(G_2\right)+16e_1{M}_1\left(G_2\right).\hfill \end{array}$$Hence, $$\begin{array}{cc}\hfill F\left(G_1{\circ }_S{G}_2\right)=& [n_2+3M_1\left(G_2\right)+6e_2]F\left(G_1\right)+[n_1+3M_1\left(G_1\right)+14e_1]F\left(G_2\right)\hfill \\ \hfill & +6e_2{M}_1\left(G_1\right)+30e_1{M}_1\left(G_2\right)+6M_1\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +F\left(G_1\right)F\left(G_2\right)+48e_1{e}_2+8n_2{e}_1.■\hfill \end{array}$$

Theorem 2

Let $G_i$ be a connected graph with $n_i$ vertices and $e_i$ edges, $i=\text{1,2}$. Then $$\begin{array}{cc}\hfill F\left(G_1{\circ }_R{G}_2\right)=& 8[n_2+6e_2]F\left(G_1\right)+[n_1+20e_1]F\left(G_2\right)+8F\left(G_1\right)F\left(G_2\right)\hfill \\ \hfill & +48e_1{e}_2+24e_2{M}_1\left(G_1\right)+36e_1{M}_1\left(G_2\right)+24M_1\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +24F\left(G_1\right)M_1\left(G_2\right)+12F\left(G_2\right)M_1\left(G_1\right)+8n_2{e}_1.\hfill \end{array}$$

Proof

$$\begin{array}{cc}\hfill F\left(G_1{\circ }_R{G}_2\right)=& \sum _{(u_1,v_1)(u_2,v_2)\in E\left(G_1{\circ }_R{G}_2\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill =& \sum _{u_1=u_2\in V\left(G_1\right)}\sum _{v_1{v}_2\in E\left(G_2\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & +\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{u_1{u}_2\in E\left(R\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & +\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{u_1{u}_2\in E\left(R\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill =& \sum {}_1+\sum {}_2+\sum {}_3.\hfill \end{array}$$Then $$\begin{array}{cc}\hfill & \sum {}_1=\sum _{u_1=u_2\in V\left(G_1\right)}\sum _{v_1{v}_2\in E\left(G_2\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =8e_2{M}_1\left(G_1\right)+n_{1}F\left(G_2\right)+4M_1\left(G_1\right)F\left(G_2\right)+8e_1{M}_1\left(G_2\right)+8M_1\left(G_1\right)M_1\left(G_2\right)+8e_{1}F\left(G_2\right)\hfill \end{array}$$since $d\left(u\right)$ in $R\left(G_1\right)$ is $2d\left(u\right)$ in $G_1$, i.e., $d_{R\left(G_1\right)}\left(u\right)=2d_{G_1}\left(u\right)$. $$\begin{array}{cc}\hfill \sum {}_2& =\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{u_1{u}_2\in E\left(R\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1,u_2\in V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & +\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(R\left(G_1\right)\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _2^{\prime }+\sum _2^{″}\hfill \end{array}$$ $$\begin{array}{cc}\hfill & \sum _2^{\prime }=\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1,u_2\in V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(G_1\right)}{u_1,u_2\in V\left(G_1\right)}}[{(d\left(u_1\right)+d\left(v\right)+d\left(u_1\right)d\left(v\right))}^2+{(d\left(u_2\right)+d\left(v\right)+d\left(u_2\right)d\left(v\right))}^2]\hfill \\ \hfill & =\sum _{v\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(G_1\right)}{u_1,u_2\in V\left(G_1\right)}}[4(d^2\left(u_1\right)+d^2\left(u_2\right))+2d^2\left(v\right)+4d^2\left(v\right)(d^2\left(u_1\right)+d^2\left(u_2\right))\hfill \\ \hfill & +4d\left(v\right)(d\left(u_1\right)+d\left(u_2\right))+4d^2\left(v\right)(d\left(u_1\right)+d\left(u_2\right))+8d\left(v_1\right)(d^2\left(u_1\right)+d^2\left(u_2\right))]\hfill \\ \hfill & =4n_{2}F\left(G_1\right)+2e_1{M}_1\left(G_2\right)+4M_1\left(G_2\right)F\left(G_1\right)+8e_2{M}_1\left(G_1\right)+4M_1\left(G_1\right)M_1\left(G_2\right)+16e_{2}F\left(G_1\right),\hfill \end{array}$$ $$\begin{array}{cc}\hfill & \sum _2^{″}=\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(R{G}_1\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(G_1\right)}{u_1\in V\left(G_1\right),u_2\in V\left(R{G}_1\right)-V\left(G_1\right)}}[{(d\left(u_1\right)+d\left(v\right)+d\left(u_1\right)d\left(v\right))}^2+{(d\left(u_2\right)+d\left(u_2\right)d\left(v\right))}^2]\hfill \end{array}$$ $$\begin{array}{cc}\hfill & =\sum _{v\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(G_1\right)}{u_1\in V\left(G_1\right),u_2\in V\left(R{G}_1\right)-V\left(G_1\right)}}[4d^2\left(u_1\right)+d^2\left(v\right)+4d^2\left(u_1\right)d^2\left(v\right)+4d\left(u_1\right)d\left(v\right)\hfill \\ \hfill & +4d\left(u_1\right)d^2\left(v\right)+8d^2\left(u_1\right)d\left(v\right)+d^2\left(u_2\right)+d^2\left(u_2\right)d^2\left(v\right)+2d^2\left(u_2\right)d\left(v\right)]\hfill \\ \hfill & =4n_{2}F\left(G_1\right)+2e_1{M}_1\left(G_2\right)+4M_1\left(G_2\right)F\left(G_1\right)+8e_2{M}_1\left(G_1\right)\hfill \\ \hfill & +4M_1\left(G_1\right)M_1\left(G_2\right)+16e_{2}F\left(G_1\right)+8n_2{e}_1+8e_1{M}_1\left(G_2\right)+32e_1{e}_2,\hfill \end{array}$$ $$\begin{array}{cc}\hfill \sum {}_2& =8(n_2+4e_2)F\left(G_1\right)+16e_2{M}_1\left(G_1\right)+12e_1{M}_1\left(G_2\right)+8M_1\left(G_2\right)F\left(G_1\right)\hfill \\ \hfill & +8M_1\left(G_1\right)M_1\left(G_2\right)+8n_2{e}_1+32e_1{e}_2.\hfill \end{array}$$ $$\begin{array}{cc}\hfill \sum {}_3& =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{u_1{u}_2\in E\left(R\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(S\left(G_1\right)\right)}{u_1,u_2\in V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & +\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(S\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(R\left(G_1\right)\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _3^{\prime }+\sum _3^{″}.\hfill \end{array}$$ $$\begin{array}{cc}\hfill & \sum _3^{\prime }=\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1,u_2\in V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1,u_2\in V\left(G_1\right)}}[{(d\left(u_1\right)+d\left(v_1\right)+d\left(u_1\right)d\left(v_1\right))}^2+{(d\left(u_2\right)+d\left(v_2\right)+d\left(u_2\right)d\left(v_2\right))}^2]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1,u_2\in V\left(G_1\right)}}[d^2\left(u_1\right)+d^2\left(u_2\right)+d^2\left(v_1\right)+d^2\left(v_2\right)+d^2\left(u_1\right)d^2\left(v_1\right)+d^2\left(u_2\right)d^2\left(v_2\right)\hfill \\ \hfill & +2d\left(u_1\right)d\left(v_1\right)+2d\left(u_2\right)d\left(v_2\right)+2d\left(u_1\right)d^2\left(v_1\right)+2d\left(u_2\right)d^2\left(v_2\right)+2d^2\left(u_1\right)d\left(v_1\right)+2d^2\left(u_2\right)d\left(v_2\right)]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1,u_2\in V\left(G_1\right)}}[4[d^2\left(u_1\right)+d^2\left(u_2\right)]+[d^2\left(v_1\right)+d^2\left(v_2\right)]+4[d^2\left(u_1\right)d^2\left(v_1\right)+d^2\left(u_2\right)d^2\left(v_2\right)]\hfill \\ \hfill & +4[d\left(u_1\right)d\left(v_1\right)+d\left(u_2\right)d\left(v_2\right)]+4[d\left(u_1\right)d^2\left(v_1\right)+d\left(u_2\right)d^2\left(v_2\right)]+8[d^2\left(u_1\right)d\left(v_1\right)+2d^2\left(u_2\right)d\left(v_2\right)]]\hfill \\ \hfill & =8e_{2}F\left(G_1\right)+2e_{1}F\left(G_2\right)+4F\left(G_1\right)F\left(G_2\right)+4M_1\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +4M_1\left(G_1\right)F\left(G_2\right)+8F\left(G_1\right)M_1\left(G_2\right),\hfill \end{array}$$ $$\begin{array}{cc}\hfill & \sum _3^{″}=\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(R\left(G_1\right)\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(R\left(G_1\right)\right)-V\left(G_1\right)}}\left[{(d\left(u_1\right)+d\left(v_1\right)+d\left(u_1\right)d\left(v_1\right))}^2{(d\left(u_2\right)+d\left(u_2\right)d\left(v_2\right))}^2\right]\hfill \end{array}$$ $$\begin{array}{cc}\hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(R\left(G_1\right)\right)-V\left(G_1\right)}}[d^2\left(u_1\right)+d^2\left(u_2\right)+d^2\left(v_1\right)+d^2\left(u_1\right)d^2\left(v_1\right)+2d\left(u_1\right)d\left(v_1\right)\hfill \\ \hfill & +2d^2\left(u_1\right)d\left(v_1\right)+2d\left(u_1\right)d^2\left(v_1\right)+d^2\left(u_2\right)d^2\left(v_2\right)+2d^2\left(u_2\right)d\left(v_2\right)]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(R\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(R\left(G_1\right)\right)-V\left(G_1\right)}}[\left[d^2\left(u_1\right)\right]+\left[d^2\left(u_2\right)\right]+\left[d^2\left(u_1\right)d^2\left(v_1\right)\right]+\left[2d\left(u_1\right)d\left(v_1\right)\right]\hfill \\ \hfill & +\left[2d^2\left(u_1\right)d\left(v_1\right)\right]+\left[d^2\left(v_1\right)\right]+\left[2d\left(u_1\right)d^2\left(v_1\right)\right]+\left[d^2\left(u_2\right)d^2\left(v_2\right)\right]+\left[2d^2\left(u_2\right)d\left(v_2\right)\right]]\hfill \\ \hfill & =8e_{2}F\left(G_1\right)+16e_1{e}_2+4F\left(G_1\right)F\left(G_2\right)+4M_1\left(G_1\right)M_1\left(G_2\right)+8F\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +2e_{1}F\left(G_2\right)+4M_1\left(G_1\right)F\left(G_2\right)+8e_{1}F\left(G_2\right)+16e_1{M}_1\left(G_2\right),\hfill \end{array}$$ $$\begin{array}{cc}\hfill \sum {}_3& =16e_{2}F\left(G_1\right)+12e_{1}F\left(G_2\right)+8F\left(G_1\right)F\left(G_2\right)+8M_1\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +16F\left(G_1\right)M_1\left(G_2\right)+8F\left(G_2\right)M_1\left(G_1\right)+16e_1{M}_1\left(G_2\right)+16e_1{e}_2.\hfill \end{array}$$Hence, $$\begin{array}{cc}\hfill F\left(G_1{\circ }_R{G}_2\right)=& 8[n_2+6e_2]F\left(G_1\right)+[n_1+20e_1]F\left(G_2\right)+8F\left(G_1\right)F\left(G_2\right)\hfill \\ \hfill & +48e_1{e}_2+24e_2{M}_1\left(G_1\right)+36e_1{M}_1\left(G_2\right)+24M_1\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +24F\left(G_1\right)M_1\left(G_2\right)+12F\left(G_2\right)M_1\left(G_1\right)+8n_2{e}_1.■\hfill \end{array}$$

Theorem 3

Let $G_i$ be a connected graph with $n_i$ vertices and $e_i$ edges, $i=\text{1, 2}$. Then $$\begin{array}{cc}\hfill F\left(G_1{\circ }_Q{G}_2\right)=& [n_2+12e_2+9M_1\left(G_2\right)]F\left(G_1\right)+[n_1+6e_1+3M_1\left(G_1\right)+6M_2\left(G_1\right)]F\left(G_2\right)\hfill \\ \hfill & +[n_2+4e_2+M_1\left(G_2\right)][M_4\left(G_1\right)+2M_2^1\left(G_1\right)+\sum _{u\in V\left(G_1\right)}{d}^2\left(u\right)\sum _{v\in N\left(u\right)}d\left(v\right)]\hfill \\ \hfill & +6[e_2{M}_1\left(G_1\right)+e_1{M}_1\left(G_2\right)+2(e_2+M_1\left(G_2\right))M_2\left(G_1\right)]\hfill \\ \hfill & +2[2F\left(G_1\right)F\left(G_2\right)+3M_1\left(G_1\right)M_1\left(G_2\right)]\hfill \end{array}$$where $M_2^1\left(G_1\right)={\sum }_{uv\in E\left(G_1\right)}$ (du+dv)dudv

Proof

$$\begin{array}{cc}\hfill F\left(G_1{\circ }_Q{G}_2\right)=& \sum _{(u_1,v_1)(u_2,v_2)\in E\left(G_1{\circ }_Q{G}_2\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill =& \sum _{u_1=u_2\in V\left(G_1\right)}\sum _{v_1{v}_2\in E\left(G_2\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & +\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & +\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill =& \sum {}_1+\sum {}_2+\sum {}_3.\hfill \end{array}$$Then $$\begin{array}{cc}\hfill & \sum {}_1=\sum _{u_1=u_2\in V\left(G_1\right)}\sum _{v_1{v}_2\in E\left(G_2\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =2e_2{M}_1\left(G_1\right)+n_{1}F\left(G_2\right)+M_1\left(G_1\right)F\left(G_2\right)+4e_1{M}_1\left(G_2\right)+2M_1\left(G_1\right)M_1\left(G_2\right)+4e_{1}F\left(G_2\right)\hfill \end{array}$$as this summation is same in $F\left(G_1{\circ }_S{G}_2\right)$. $$\begin{array}{cc}\hfill \sum {}_2& =\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V(\left(Q{G}_1\right)-V\left(G_1\right))}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & +\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1,u_2\in V\left(Q\left(G_1\right)\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _2^{\prime }+\sum _2^{″}.\hfill \end{array}$$ $$\begin{array}{cc}\hfill \sum _2^{\prime }& =\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(Q{G}_1\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q{G}_1\right)}{u_1\in V\left(G_1\right),u_2\in V\left(Q{G}_1\right)-V\left(G_1\right)}}[{(d\left(u_1\right)+d\left(v\right)+d\left(u_1\right)d\left(v\right))}^2+{(d\left(u_2\right)+d\left(u_2\right)d\left(v\right))}^2]\hfill \\ \hfill & =\sum _{v\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(G_1\right)}{u_1\in V\left(G_1\right),u_2\in V\left(Q{G}_1\right)-V\left(G_1\right)}}[d^2\left(u_1\right)+d^2\left(v\right)+d^2\left(u_1\right)d^2\left(v\right)+2d\left(u_1\right)d\left(v\right)\hfill \\ \hfill & +2d\left(u_1\right)d^2\left(v\right)+2d^2\left(u_1\right)d\left(v\right)+d^2\left(u_2\right)+d^2\left(u_2\right)d^2\left(v\right)+2d^2\left(u_2\right)d\left(v\right)]\hfill \end{array}$$Consider $$S_1=\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q{G}_1\right)}{u_1\in V\left(G_1\right),u_2\in V\left(Q{G}_1\right)-V\left(G_1\right)}}{d}^2\left(u_1\right)$$In $S_1$, $u_1\in V\left(G_1\right)$ and $d^2{u}_1$ occurs $d{u}_1$ times. Thus $$S_1=\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q{G}_1\right)}{u_1\in V\left(G_1\right),u_2\in V\left(Q{G}_1\right)-V\left(G_1\right)}}{d}^3\left(u_1\right)=F\left(G_1\right).$$Let $$S_2=\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q{G}_1\right)}{u_1\in V\left(G_1\right),u_2\in V\left(Q{G}_1\right)-V\left(G_1\right)}}{d}^2\left(u_2\right)$$as $u_2=uv\in E\left(G_1\right)$, $d^2{u}_2$ occurs two times. Therefore $$\begin{array}{cc}\hfill S_2=2\sum _{u_2=uv\in V\left(Q{G}_1\right)-V\left(G_1\right)}{[du+dv]}^2& =2\sum _{uv\in E\left(G_1\right)}[d^{2}u+d^{2}v+2dudv]\hfill \\ \hfill & =2[F\left(G_1\right)+2M_2\left(G_1\right)]\hfill \end{array}$$Hence $$\begin{array}{cc}\hfill \sum _2^{\prime }& =n_{2}F\left(G_1\right)+2e_1{M}_1\left(G_2\right)+M_1\left(G_2\right)F\left(G_1\right)+4e_2{M}_1\left(G_1\right)+4e_{2}F\left(G_1\right)+2M_1\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +2n_2[F\left(G_1\right)+2M_2\left(G_1\right)]+2M_1\left(G_2\right)[F\left(G_1\right)+2M_2\left(G_1\right)]+8e_2[F\left(G_1\right)+2M_2\left(G_1\right)]\hfill \end{array}$$ $$\begin{array}{cc}\hfill \sum _2^{″}& =\sum _{v_1=v_2\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1,u_2\in V\left(Q{G}_1\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q{G}_1\right)}{u_1,u_2\in V\left(Q{G}_1\right)-V\left(G_1\right)}}[{(d\left(u_1\right)+d\left(u_1\right)d\left(v\right))}^2+{(d\left(u_2\right)+d\left(u_2\right)d\left(v\right))}^2]\hfill \\ \hfill & =\sum _{v\in V\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q{G}_1\right)}{u_1,u_2\in V\left(Q{G}_1\right)-V\left(G_1\right)}}[[d^2\left(u_1\right)+d^2\left(u_2\right)]+d^2\left(v\right)[d^2\left(u_1\right)+d^2\left(u_2\right)]\hfill \\ \hfill & +2d\left(v\right)[d^2\left(u_1\right)+d^2\left(u_2\right)]]\hfill \end{array}$$Consider $$S_3=\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q{G}_1\right)}{u_1,u_2\in V\left(Q{G}_1\right)-V\left(G_1\right)}}[d^2\left(u_1\right)+d^2\left(u_2\right)]$$In $S_3$, coefficient of $d^{2}u$ = 2 $C_{d_{G_1}\left(u\right)}^2$ + ${\sum }_{v\in N\left(u\right)}$ d(v) – d(u)

= $d^2\left(u\right)$ – 2d(u) + ${\sum }_{v\in N\left(u\right)}$ d(v)

Therefore, $$\begin{array}{cc}\hfill \sum _{u\in V\left(G_1\right)}{d}^2\left(u\right)& =\sum _{u\in V\left(G_1\right)}[d^2\left(u\right)-2d\left(u\right)+\sum _{v\in N\left(u\right)}d\left(v\right)]d^2\left(u\right)\hfill \\ \hfill & =M_4\left(G_1\right)-2F\left(G_1\right)+\sum _{u\in V\left(G_1\right)}{d}^2\left(u\right)\sum _{v\in N\left(u\right)}d\left(v\right)\hfill \end{array}$$For coefficient of dudv, let $u_1{u}_2\in E\left(Q{G}_1\right)$ with $u_1=uv$ and $u_2=wz$. As $u_1{u}_2\in E\left(Q{G}_1\right)$, we have either $v=w$ or $z$ or $u=w$ or $z$. So $uv$ is adjacent to all those vertices in $G_1$ which are adjacent to $u$ and $v$. So number of such $dudv$ is ($du+dv-2$).

Therefore, $$\begin{array}{cc}\hfill 2\sum _{uv\in E\left(G_1\right)}dudv& =2\sum _{uv\in E\left(G_1\right)}(du+dv-2)dudv\hfill \\ \hfill & =2\sum _{uv\in E\left(G_1\right)}(du+dv)dudv-4\sum _{uv\in E\left(G_1\right)}dudv\hfill \\ \hfill & =2M_2^1\left(G_1\right)-4M_2\left(G_1\right)\hfill \\ \hfill So,\\ \hfill S_3& =M_4\left(G_1\right)-2F\left(G_1\right)+\sum _{u\in V\left(G_1\right)}{d}^2\left(u\right)\sum _{v\in N\left(u\right)}d\left(v\right)\hfill \\ \hfill & +2M_2^1\left(G_1\right)-4M_2\left(G_1\right)\hfill \end{array}$$ $$\begin{array}{cc}\hfill So\sum _2^{″}& =[n_2+4e_2+M_1\left(G_2\right)][M_4\left(G_1\right)-2F\left(G_1\right)+2M_2^1\left(G_1\right)-4M_2\left(G_1\right)]\hfill \\ \hfill & +\sum _{u\in V\left(G_1\right)}{d}^2\left(u\right)\sum _{v\in N\left(u\right)}d\left(v\right)\hfill \end{array}$$ $$\begin{array}{cc}\hfill \sum {}_2& =2[e_1+M_{!}\left(G_1\right)]M_1\left(G_2\right)+4e_2{M}_1\left(G_1\right)+[n_2+4e_2+M_1\left(G_2\right)][M_4\left(G_1\right)+F\left(G_1\right)\hfill \\ \hfill & +\sum _{u\in V\left(G_1\right)}{d}^2\left(u\right)\sum _{v\in N\left(u\right)}d\left(v\right)+2M_2^1\left(G_1\right)]\hfill \end{array}$$ $$\begin{array}{cc}\hfill \sum {}_3& =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(Q\left(G_1\right)\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & +\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1,u_2\in V\left(Q\left(G_1\right)\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _3^{\prime }+\sum _3^{″}.\hfill \end{array}$$ $$\begin{array}{cc}\hfill \sum _3^{\prime }& =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(Q\left(G_1\right)\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(Q\left(G_1\right)\right)-V\left(G_1\right)}}[{(d\left(u_1\right)+d\left(v_1\right)+d\left(u_1\right)d\left(v_1\right))}^2+{(d\left(u_2\right)+d\left(u_2\right)d\left(v_2\right))}^2]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1\in V\left(G_1\right),u_2\in V\left(Q\left(G_1\right)\right)-V\left(G_1\right)}}[d^2\left(u_1\right)+d^2\left(u_1\right)d^2\left(v_1\right)+2d\left(u_1\right)d\left(v_1\right)+2d\left(u_1\right)d^2\left(v_1\right)\hfill \\ \hfill & +2d^2\left(u_1\right)d\left(v_1\right)+d^2\left(v_1\right)+d^2\left(u_2\right)+d^2\left(u_2\right)d^2\left(v_2\right)+2d^2\left(u_2\right)d\left(v_2\right)]\hfill \\ \hfill & =2e_{2}F\left(G_1\right)+F\left(G_1\right)F\left(G_2\right)+2M_1\left(G_1\right)M_1\left(G_2\right)+2M_1\left(G_1\right)F\left(G_2\right)+2F\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +2e_{1}F\left(G_2\right)+[4e_2+2F\left(G_2\right)+4M_1\left(G_2\right)][F\left(G_1\right)+2M_2\left(G_1\right)]\hfill \\ \hfill & =6[e_2+M_1\left(G_2\right)]F\left(G_1\right)+3F\left(G_1\right)F\left(G_2\right)+2M_1\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +2[e_1+M_1\left(G_1\right)+2M_2\left(G_1\right)]F\left(G_2\right)+8M_2\left(G_1\right)[e_2+M_1\left(G_2\right)],\hfill \end{array}$$ $$\begin{array}{cc}\hfill \sum _3^{″}& =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1,u_2\in V\left(Q\left(G_1\right)\right)-V\left(G_1\right)}}[d{(u_1,v_1)}^2+d{(u_2,v_2)}^2]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1,u_2\in V\left(Q\left(G_1\right)\right)-V\left(G_1\right)}}\left[{(d\left(u_1\right)+d\left(u_1\right)d\left(v_1\right))}^2{(d\left(u_2\right)+d\left(u_2\right)d\left(v_2\right))}^2\right]\hfill \\ \hfill & =\sum _{v_1{v}_2\in E\left(G_2\right)}\sum _{\genfrac{}{}{0ex}{}{u_1{u}_2\in E\left(Q\left(G_1\right)\right)}{u_1,u_2\in V\left(Q\left(G_1\right)\right)-V\left(G_1\right)}}[[d^2\left(u_1\right)+d^2\left(u_2\right)]+[d^2\left(u_1\right)d^2\left(v_1\right)+d^2\left(u_2\right)d^2\left(v_2\right)]\hfill \\ \hfill & +2[d^2\left(u_1\right)d\left(v_1\right)+d^2\left(u_2\right)d\left(v_2\right)]]\hfill \\ \hfill & =2e_2[F\left(G_1\right)+2M_2\left(G_1\right)]+F\left(G_2\right)[F\left(G_1\right)+2M_2\left(G_1\right)]+2M_1\left(G_2\right)[F\left(G_1\right)+2M_2\left(G_1\right)],\hfill \end{array}$$ $$\begin{array}{cc}\hfill \sum {}_3& =8[e_2+M_1\left(G_2\right)]F\left(G_1\right)+4F\left(G_1\right)F\left(G_2\right)+2M_1\left(G_1\right)M_1\left(G_2\right)\hfill \\ \hfill & +2[e_1+M_1\left(G_1\right)+3M_2\left(G_1\right)]F\left(G_2\right)+12[e_2+M_1\left(G_2\right)]M_2\left(G_1\right).\hfill \end{array}$$Hence, $$\begin{array}{cc}\hfill F\left(G_1{\circ }_Q{G}_2\right)=& [n_2+12e_2+9M_1\left(G_2\right)]F\left(G_1\right)+[n_1+6e_1+3M_1\left(G_1\right)+6M_2\left(G_1\right)]F\left(G_2\right)\hfill \\ \hfill & +[n_2+4e_2+M_1\left(G_2\right)][M_4\left(G_1\right)+2M_2^1\left(G_1\right)+\sum _{u\in V\left(G_1\right)}{d}^2\left(u\right)\sum _{v\in N\left(u\right)}d\left(v\right)]\hfill \\ \hfill & +6[e_2{M}_1\left(G_1\right)+e_1{M}_1\left(G_2\right)+2(e_2+M_1\left(G_2\right))M_2\left(G_1\right)]\hfill \\ \hfill & +2[2F\left(G_1\right)F\left(G_2\right)+3M_1\left(G_1\right)M_1\left(G_2\right)]■\hfill \end{array}$$

Combining Theorems 2 and 3 we get

Theorem 4

$$\begin{array}{cc}\hfill F\left(G_1{\circ }_T{G}_2\right)& =[8n_2+54e_2]F\left(G_1\right)+[n_1+12e_1]F\left(G_2\right)+11F\left(G_1\right)F\left(G_2\right)+24e_2{M}_1\left(G_1\right)\hfill \\ \hfill & +12[e_1{M}_1\left(G_2\right)+e_2{M}_2\left(G_1\right)]+24M_1\left(G_1\right)M_1\left(G_2\right)+12M_1\left(G_1\right)F\left(G_2\right)\hfill \\ \hfill & +30F\left(G_1\right)M_1\left(G_2\right)+6M_2\left(G_1\right)[2M_1\left(G_2\right)+F\left(G_2\right)]\hfill \\ \hfill & +[n_2+M_1\left(G_2\right)+4e_2][M_4\left(G_1\right)+2M_2^1\left(G_1\right)+\sum _{u\in V\left(G_1\right)}{d}^2\left(u\right)\sum _{v\in N\left(u\right)}d\left(v\right)]\hfill \end{array}$$

Example 1

Applying theorems above to the graphs $G_1=P_m$ and $G_2=P_n$, we have $n_1=\left|V\left(G_1\right)\right|=m$, $n_2=\left|V\left(G_2\right)\right|=n$, $e_1=\left|E\left(G_1\right)\right|=m-1$, $e_2=\left|E\left(G_1\right)\right|=n-1$, $M_1\left(G_1\right)=4m-6$, $M_1\left(G_2\right)=4n-6$, $M_2\left(G_1\right)=4(m-2)$, where $m>2$, $M_2\left(G_2\right)=4(n-2)$, where $n>2$, $M_4\left(G_1\right)=16m-30$, $M_2^1\left(G_1\right)=16m-36$, where $m\ge 3$, ${\sum }_{u\in V\left(G_1\right)}$ $d^2\left(u\right)$ ${\sum }_{v\in N\left(u\right)}d\left(v\right)=16m-36$, $F\left(G_1\right)=8m-14$ and $F\left(G_2\right)=8n-14$. And $$\begin{array}{cc}\hfill F\left(P_m{\circ }_S{P}_n\right)& =728mn-1078m-990n+1460,\text{if}m\ge 2,n\ge 2;\hfill \\ \hfill F\left(P_m{\circ }_R{P}_n\right)& =2960mn-4334m-4680n+6816,\text{if}m\ge 2,n\ge 2;\hfill \\ \hfill F\left(P_m{\circ }_Q{P}_n\right)& =1952mn-2758m-3636n+5056,\text{if}m\ge 3,n\ge 2;\hfill \\ \hfill F\left(P_m{\circ }_T{P}_n\right)& =4184mn-6014m-7326n+10412,\text{if}m\ge 3,n\ge 2.\hfill \end{array}$$

Example 2

Applying theorems above to the graphs $G_1=C_m$ and $G_2=C_n$, we have $n_1=\left|V\left(G_1\right)\right|=m$, $n_2=\left|V\left(G_2\right)\right|=n$, $e_1=\left|E\left(G_1\right)\right|=m$, $e_2=\left|E\left(G_1\right)\right|=n$, $M_1\left(G_1\right)=4\mathrm{m}$, $M_1\left(G_2\right)=4n$, $M_2\left(G_1\right)=4\mathrm{m}$, $M_2\left(G_2\right)=4n$, where $m,n\ge 3$, $M_4\left(G_1\right)=16\mathrm{m}$, $M_2^1\left(G_1\right)=16\mathrm{m}$, ${\sum }_{u\in V\left(G_1\right)}$ $d^2\left(u\right)$ ${\sum }_{v\in N\left(u\right)}d\left(v\right)=16\mathrm{m}$, $F\left(G_1\right)=8\mathrm{m}$, $F\left(G_2\right)=8n$. And $$\begin{array}{cc}\hfill F\left(C_m{\circ }_S{C}_n\right)& =728mn,\text{if}m,n\ge 3;\hfill \\ \hfill F\left(C_m{\circ }_R{C}_n\right)& =2960mn,\text{if}m,n\ge 3;\hfill \\ \hfill F\left(C_m{\circ }_Q{C}_n\right)& =1952mn,\text{if}m,n\ge 3;\hfill \\ \hfill F\left(C_m{\circ }_T{C}_n\right)& =4184mn,\text{if}m,n\ge 3.\hfill \end{array}$$

Example 3

Applying theorems above to the graphs $G_1=P_m$ and $G_2=C_n$, we have $n_1=\left|V\left(G_1\right)\right|=m$, $n_2=\left|V\left(G_2\right)\right|=n$, $e_1=\left|E\left(G_1\right)\right|=m-1$, $e_2=\left|E\left(G_1\right)\right|=n$, $M_1\left(G_1\right)=4m-6$, $M_1\left(G_2\right)=4n$, $M_2\left(G_1\right)=4m-8$, $M_2\left(G_2\right)=4n$, where $m\ge 2$, $n\ge 3$, $M_4\left(G_1\right)=16m-30$, $M_2^1\left(G_1\right)=16m-36$, where $m\ge 3$, ${\sum }_{u\in V\left(G_1\right)}$ $d^2\left(u\right)$ ${\sum }_{v\in N\left(u\right)}d\left(v\right)=16m-36$, $F\left(G_1\right)=8m-14$, $F\left(G_2\right)=8n$. And $$\begin{array}{cc}\hfill F\left(P_m{\circ }_S{C}_n\right)& =728mn-990n,\text{if}m\ge 2,n\ge 3;\hfill \\ \hfill F\left(P_m{\circ }_R{C}_n\right)& =2960mn-4680n,\text{if}m\ge 2,n\ge 3;\hfill \\ \hfill F\left(P_m{\circ }_Q{C}_n\right)& =1952mn-3636n,\text{if}m,n\ge 3;\hfill \\ \hfill F\left(P_m{\circ }_T{C}_n\right)& =4184mn-7326n,\text{if}m,n\ge 3.\hfill \end{array}$$

3 Summary and conclusions

In this work, we study the F index of graphs $G_1{\circ }_F{G}_2$ based on operations related to the strong product, subdivision and total graph, and obtain the expressions for $F\left(G_1{\circ }_S{G}_2\right)$, $F\left(G_1{\circ }_R{G}_2\right)$ , $F\left(G_1{\circ }_Q{G}_2\right)$ and $F\left(G_1{\circ }_T{G}_2\right)$ in terms of F indices of $G_1,G_2$, the first Zagreb indices of $G_1,G_2$, and the second Zagreb index of $G_2$, and use them to compute the F index of $P_m{\circ }_F{P}_n$, $C_m{\circ }_F{C}_n$ and $P_m{\circ }_F{C}_n$.