On -domination in graphs

Abstract

Let $G=(V,E)$ be a graph and let $\mathcal{F}$ be a family of subsets of $V$ such that ${\bigcup }_{F\in \mathcal{F}}F=V.$ A dominating set $D$ of $G$ is called an $\mathcal{F}$-dominating set if $D\cap F\ne \varnothing$ for all $F\in \mathcal{F}.$ The minimum cardinality of an $\mathcal{F}$-dominating of $G$ is called the $\mathcal{F}$-domination number of $G$ and is denoted by ${\gamma }_{\mathcal{F}}\left(G\right).$ In this paper we present several basic results on this parameter. We also introduce the concept of $\mathcal{F}$-irredundance and obtain an inequality chain four parameters.

Keywords:

• Domination
• $\mathcal{F}$-domination
• $\mathcal{F}$-domination number
• $\mathcal{F}$-irredundance

1 Introduction

By a graph $G=(V,E)$ we mean a finite undirected graph with neither loops nor multiple edges. The order $\left|V\right|$ and the size $\left|E\right|$ are denoted by $n$ and $m$ respectively. For graph theoretic terminology we refer to Chartrand and Lesniak [1]. The main focus of this paper is a generalization of the concept of domination in graphs. For an excellent treatment of fundamentals of domination we refer to the book by Haynes et al. [2]. For survey of several advanced topics in domination we refer to the book edited by Haynes et al. [3].

Let $G=(V,E)$ be a graph. A subset $S$ of $V$ is called a dominating set of $G$ if every vertex in $V\setminus S$ is adjacent to a vertex in $S.$ A dominating set $S$ is called a minimal dominating set if no proper subset of $S$ is a dominating set. The minimum cardinality of a dominating set of $G$ is called the domination number of $G$ and is denoted by $\gamma \left(G\right).$ The maximum cardinality of a minimal dominating set of $G$ is called the upper domination number of $G$ and is denoted by $\Gamma \left(G\right).$ A subset $S$ of $V$ is called an independent set if no two vertices in $S$ are adjacent. An independent set $S$ is called a maximal independent set if no proper superset of $S$ is an independent set. The minimum cardinality of a maximal independent set of $G$ is called the independent domination number of $G$ and is denoted by $i\left(G\right).$ The maximum cardinality of an independent set of $G$ is called the independence number of $G$ and is denoted by ${\beta }_0\left(G\right).$ Let $S$ be a set of vertices and let $u\in S$. We say that a vertex $v$ is a private neighbor of $u$ with respect $S$ if $N\left[v\right]\cap S=\left\{u\right\}$. The private neighbor set $pn[u,S]$ of $u$ with respect to $S$ is defined by $pn[u,S]=\{v:N\left[v\right]\cap S=\left\{u\right\}\}$. We say that a set $S$ of vertices is irredundant if $pn[v,S]\ne \varphi$ for every $v\in S$. An irredundant set $S$ is said to be maximal, if no superset of $S$ is an irredundant set. The minimum cardinality of a maximal irredundant set in $G$ is called the irredundance number of $G$ and is denoted by $ir\left(G\right)$. Similarly, the maximum cardinality of an irredundant set in $G$ is called the upper irredundance number of $G$ and is denoted by $IR\left(G\right)$. The following inequality chain was first observed by Cockayne et al. [4].

Theorem 1.1

For any graph $G$,

$ir\left(G\right)\le \gamma \left(G\right)\le i\left(G\right)\le {\beta }_0\left(G\right)\le \Gamma \left(G\right)\le IR\left(G\right)$.

The above inequality chain is called the domination chain of $G$ and has become one of the strongest focal points of research in domination theory.

Let $X$ be a finite nonempty set and let $\mathcal{E}$ be a collection of subsets of $X.$ The pair $\mathcal{H}=(X,\mathcal{E})$ is called a hypergraph. The elements of $X$ are called vertices and the elements of $\mathcal{E}$ are called edges. We assume that ${\bigcup }_{E\in \mathcal{E}}E=X$ and $1\le \left|E\right|\le \left|X\right|-1$ for all $E\in \mathcal{E}.$ A hypergraph $\mathcal{H}$ is called simple if no edge is a proper subset of another edge. An edge $E$ of $\mathcal{H}$ is called a hyperedge if $\left|E\right|\ge 3$ and $\mathcal{H}$ is called a pure hypergraph if every edge of $\mathcal{H}$ is a hyperedge. A subset $T$ of $X$ is called a transversal of $\mathcal{H}$ if $T\cap E\ne \varnothing$ for all $E\in \mathcal{E}.$ The minimum cardinality of a transversal of $\mathcal{H}$ is called the transversal number of $\mathcal{H}$ and is denoted by $\tau \left(\mathcal{H}\right).$

Several types of domination parameters have been reported in literature and more than 65 models of domination are given in the appendix of [2].

In a social network there are several subsets of the vertex set representing a set of people with common interest and hence it is natural to consider a dominating set $D$ in which each such subset has at least one representation in $D.$ This motivates the concept of $\mathcal{F}$-domination which is the main focus of this paper.

2 Basic results

Definition 2.1

Let $G=(V,E)$ be a graph and let $\mathcal{F}$ be a family of subsets of $V$ whose union is $V.$ A dominating set $D$ of $G$ is called an $\mathcal{F}$-dominating set if $D\cap F\ne \varnothing$ for all $F\in \mathcal{F}.$ The minimum cardinality of an $\mathcal{F}$-dominating set of $G$ is called the $\mathcal{F}$-domination number of $G$ and is denoted by ${\gamma }_{\mathcal{F}}\left(G\right).$

Clearly a dominating set $D$ of $G$ is an $\mathcal{F}$-dominating set if and only if $D$ is a dominating set and is a transversal of the hypergraph $\mathcal{H}=(V,\mathcal{F}).$

Observation 2.2

If $\mathcal{F}=\left\{V\right\},$ then ${\gamma }_{\mathcal{F}}\left(G\right)=\gamma \left(G\right).$ Also if ${\mathcal{F}}_1\subseteq {\mathcal{F}}_2,$ then ${\gamma }_{{\mathcal{F}}_1}\left(G\right)\le {\gamma }_{{\mathcal{F}}_2}\left(G\right).$

Observation 2.3

If ${\mathcal{F}}_1=\{\left\{v\right\}:v\in V\}$and ${\mathcal{F}}_1\subseteq \mathcal{F},$ then ${\gamma }_{\mathcal{F}}\left(G\right)=n.$ The converse is not true. For the graph $G=(V,E)$ where $V=\{a,b,c,d\},E=\left\{ab\right\}$and $\mathcal{F}=\{\left\{a\right\},\left\{b\right\},\{c,d\}\},$ we have ${\gamma }_{\mathcal{F}}\left(G\right)=n=4.$ For a graph $G$ without isolated vertices, the converse is true as shown in the following theorem.

Theorem 2.4

Let $G$ be a graph without isolated vertices. Then ${\gamma }_{\mathcal{F}}\left(G\right)=n$ if and only if $\{\left\{v\right\}:v\in V\}\subseteq \mathcal{F}.$

Proof

Let ${\gamma }_{\mathcal{F}}\left(G\right)=n.$ Suppose there exists $u\in V$ such that $\left\{u\right\}\notin \mathcal{F}.$ Since $G$ has no isolated vertices, it follows that $V\left(G\right)-\left\{u\right\}$ is an $\mathcal{F}$-dominating set of $G.$ Hence ${\gamma }_{\mathcal{F}}\left(G\right)<n,$ which is a contradiction. The converse is obvious.

Theorem 2.5

Let $G$ be a graph without isolated vertices and let $k$ be an integer with $1\le k\le \left|V\right|=n.$ Let $\mathcal{F}=\{F\subseteq V:\left|F\right|=k\}.$ Then ${\gamma }_{\mathcal{F}}\left(G\right)\ge n-k+1.$

Proof

Let $D\subseteq V\left(G\right)$ and $\left|D\right|\le n-k.$ Then $|V-D|\ge k.$ For any subset $F\subseteq V-D$ with $\left|F\right|=k,$ we have $F\in \mathcal{F}$ and $D\cap F=\varnothing .$ Hence $D$ is not an $\mathcal{F}$-dominating set of $G,$ so that ${\gamma }_{\mathcal{F}}\left(G\right)\ge n-k+1.$

Corollary 2.6

Let $G$ be a graph without isolated vertices. Let $\mathcal{F}=\{F\subseteq V:\left|F\right|=2\}.$ Then ${\gamma }_{\mathcal{F}}\left(G\right)=n-1.$

Proof

It follows from Theorems 2.4 and 2.5 that ${\gamma }_{\mathcal{F}}\left(G\right)<n$ and ${\gamma }_{\mathcal{F}}\left(G\right)\ge n-1.$ Hence ${\gamma }_{\mathcal{F}}\left(G\right)=n-1.$

Corollary 2.7

Let $G$ be a graph without isolated vertices and let $\mathcal{F}=\{F\subseteq V:\left|F\right|=2\}.$ Let $\mathcal{H}=(V,\mathcal{F}).$ Then ${\gamma }_{\mathcal{F}}\left(G\right)=\mathcal{T}\left(\mathcal{H}\right).$

Proof

Since the hypergraph $\mathcal{H}$ is isomorphic to the complete graph, its transversal number $\tau \left(\mathcal{H}\right)=n-1.$ Thus ${\gamma }_{\mathcal{F}}\left(G\right)=\mathcal{T}\left(\mathcal{H}\right)=n-1.$

Theorem 2.8

Let $G=(V,E)$ be a graph and let $k$ be a positive integer. Let $\mathcal{P}=\{\mathcal{F}:\mathcal{F}isapartitionofVand{\gamma }_{\mathcal{F}}\left(G\right)=k\}.$ Then ${max}_{\mathcal{F}\in \mathcal{P}}\left|\mathcal{F}\right|=k.$

Proof

Let $\mathcal{F}\in \mathcal{P}$ and let $D$ be an $\mathcal{F}$-dominating set of $G$ with $\left|D\right|={\gamma }_{\mathcal{F}}\left(G\right).$ Since $D\cap F\ne \varnothing$ for all $F\in \mathcal{F}$ and $\mathcal{F}$ is a partition of $V,$ it follows that $k={\gamma }_{\mathcal{F}}\left(G\right)=\left|D\right|\ge \left|\mathcal{F}\right|.$ Hence ${max}_{\mathcal{F}\in \mathcal{P}}\left|\mathcal{F}\right|\le k.$ Also if $D=\{v_1,v_2,\dots ,v_k\},$ then $\mathcal{F}=\{\left\{v_i\right\}:1\le i<k\}\cup \{(V-D)\cup \left\{v_k\right\}\}$ is a partition of $V$ with ${\gamma }_{\mathcal{F}}\left(G\right)=k.$ Hence $\mathcal{F}\in \mathcal{P}$ and $\left|\mathcal{F}\right|=k,$ so that ${max}_{\mathcal{F}\in \mathcal{P}}\left|\mathcal{F}\right|=k.$

Theorem 2.9

Let $G=(V,E)$ be a graph and let $k$ be a positive integer. Let $\mathcal{C}=\{\mathcal{F}:{\gamma }_{\mathcal{F}}\left(G\right)=k\}.$ Then ${max}_{\mathcal{F}\in \mathcal{C}}\left|\mathcal{F}\right|=2^n-2^{n-k}.$

Proof

Let $\mathcal{F}\in \mathcal{C}$ and let $D$ be an $\mathcal{F}$-dominating set of $G$ with $\left|D\right|=k.$ Since $D\cap F\ne \varnothing$ for all $F\in \mathcal{F}$ it follows that any $F\in \mathcal{F}$ is of the form $F=D_1\cup D_2$ where $D_1$ is a nonempty subset of $D$ and $D_2$ is a subset of $V-D.$ Hence $\left|\mathcal{F}\right|\le 2^{n-k}(2^k-1)=2^n-2^{n-k}.$ Thus ${max}_{\mathcal{F}\in \mathcal{C}}\left|\mathcal{F}\right|\le 2^n-2^{n-k}.$

Now, let $\mathcal{F}=\{D_1\cup D_2:D_1\subseteq D$ and $D_1\ne \varnothing$ and $D_2\subseteq V-D\}.$ Then ${\gamma }_{\mathcal{F}}\left(G\right)=k$ and hence $\mathcal{F}\in \mathcal{C}.$ Also $\left|\mathcal{F}\right|=2^n-2^{n-k}$ and so ${max}_{\mathcal{F}\in \mathcal{C}}\left|\mathcal{F}\right|=2^n-2^{n-k}.$

Observation 2.10

Let $\mathcal{F}$ be a collection of subsets of $V$ whose union is $V.$ Then ${\gamma }_{\mathcal{F}}\left(G\right)=1$ if and only if there exists $u\in V$ such that $degu=n-1$ and $u\in F$ for all $F\in \mathcal{F}.$ In particular if $\mathcal{F}$ is a partition of $V,$ then ${\gamma }_{\mathcal{F}}\left(G\right)=1$ if and only if there exists $u\in V$ such that $degu=n-1$ and $\mathcal{F}=\left\{V\right\}.$

Theorem 2.11

Let $a,b$ and $n$ be positive integers with $a\le b\le n.$ Let $G$ be any graph of order $n$ with $\gamma \left(G\right)=a.$ Then there exists a family of subsets $\mathcal{F}$ such that ${\gamma }_{\mathcal{F}}\left(G\right)=b.$

Proof

Let $D$ be a $\gamma$-set of $G.$ If $a=b$, we take, $\mathcal{F}=\left\{V\right\}$. Suppose $a<b$. Since $\left|D\right|=\gamma \left(G\right)=a<b\le n$, we have $|V-D|=n-a\ge b-a$. Hence there exists a subset $S$ of $V-D$ such that $\left|S\right|=b-a-1$. Now, let $\mathcal{F}=\{\left\{x\right\}:x\in D\cup S\}\cup \{V-(D\cup S)\}$. Clearly, ${\gamma }_{\mathcal{F}}\left(G\right)=b.$

Observation 2.12

Let $H$ be an induced subgraph $G.$ Let $\mathcal{F}$ be a family of subsets of $V\left(G\right)$ and let ${\mathcal{F}}_1=\{F\cap V\left(H\right):F\in \mathcal{F}$ and $F\cap V\left(H\right)\ne \varnothing \}.$ Then there is no relation between ${\gamma }_{\mathcal{F}}\left(G\right)$ and ${\gamma }_{{\mathcal{F}}_1}\left(H\right).$

For example let $G=W_n=C_{n-1}+\left\{u\right\}$and let $H=C_{n-1}.$ Let $\mathcal{F}=\{\left\{u\right\},V\left(C_{n-1}\right)\}.$ Then ${\mathcal{F}}_1=\left\{V\left(C_{n-1}\right)\right\}.$

Now ${\gamma }_{\mathcal{F}}\left(G\right)=2$ and $${\gamma }_{{\mathcal{F}}_1}\left(H\right)=\left\{\begin{array}{cc}1\hfill & \text{if}n=4\hfill \\ 2\hfill & \text{if}n=\text{5, 6}\text{or 7}\hfill \\ ⌈\frac{n}{3}⌉\hfill & \text{if}n\ge 8.\hfill \end{array}\right.$$Thus ${\gamma }_{\mathcal{F}}\left(G\right)>{\gamma }_{{\mathcal{F}}_1}\left(H\right)$ if $n=4,$ ${\gamma }_{\mathcal{F}}\left(G\right)={\gamma }_{{\mathcal{F}}_1}\left(H\right)$ if $n=\text{5, 6}$ or 7 and ${\gamma }_{\mathcal{F}}\left(G\right)<{\gamma }_{{\mathcal{F}}_1}\left(H\right)$ if $n\ge 8.$

Hence the study of the effect on $\gamma {}_{\mathcal{F}}\left(G\right)$ when a vertex is deleted is an interesting area of research and results in this direction will be reported in a subsequent paper.

Theorem 2.13

Let $G$ be a graph and let $\mathcal{F}=\{F_1,F_2,\dots ,F_k\}$ be a partition of $V\left(G\right)$. Then ${\gamma }_{\mathcal{F}}\left(G\right)=\left|\mathcal{F}\right|$ if and only if there exists a dominating set $D$ of $G$ such that $|D\cap F_i|=1$, for $i=1,2,\dots ,k$.

Proof

Suppose ${\gamma }_{\mathcal{F}}\left(G\right)=\left|\mathcal{F}\right|$. Let $D$ be a ${\gamma }_{\mathcal{F}}$-set of $G$. Then $\left|D\right|={\gamma }_{\mathcal{F}}\left(G\right)=\left|\mathcal{F}\right|$ and $D\cap F_i\ne \varphi$ for all $i$. Hence it follows that $|D\cap F_i|=1$.

Conversely, suppose that there exists a dominating set $D$ of $G$ such that $|D\cap F_i|=1$, for $i=1,2,\dots ,k$. Clearly $D$ is an $\mathcal{F}$-dominating set of $G$ and $\left|D\right|=k=\left|\mathcal{F}\right|$. Hence ${\gamma }_{\mathcal{F}}\left(G\right)=\left|\mathcal{F}\right|$.

3 $\mathcal{F}$-irredundance in graphs

Since $\mathcal{F}$-Domination is a superhereditary property, minimality is equivalent to $1$-minimality ([2] page. 68). The following theorem is a characterization of minimal $\mathcal{F}$-Dominating sets.

Theorem 3.1

An $\mathcal{F}$-dominating set $D$ of $G$ is a minimal $\mathcal{F}$-dominating set if and only if for every $d\in D$, one of the following holds.

(1) $D-\left\{d\right\}$is not a dominating set of $G$

(2) There exists $F\in \mathcal{F}$ such that $D\cap F=\left\{d\right\}$.

Proof

Suppose $D$ is a minimal $\mathcal{F}$-dominating set of $G$ and $d\in D$. Then $D-\left\{d\right\}$ is not an $\mathcal{F}$-dominating set. Hence either $D-\left\{d\right\}$ is not a dominating set of $G$ or $(D-\left\{d\right\})\cap F=\varphi$, for some $F\in \mathcal{F}$. Hence either (1) or (2) holds.

The converse is obvious.

Definition 3.2

The maximum cardinality of a minimal $\mathcal{F}$-dominating set is called the upper $\mathcal{F}$-domination number of $G$ and is denoted by ${\Gamma }_{\mathcal{F}}\left(G\right)$ of $G$.

Clearly ${\gamma }_{\mathcal{F}}\left(G\right)\le {\Gamma }_{\mathcal{F}}\left(G\right)$. The following theorem shows that the difference ${\Gamma }_{\mathcal{F}}\left(G\right)-{\gamma }_{\mathcal{F}}\left(G\right)$ can be arbitrarily large.

Theorem 3.3

Let $a$ and $b$ be two positive integers with $a\le b$. Then there exists a graph $G$ and an $\mathcal{F}$ such that ${\gamma }_{\mathcal{F}}\left(G\right)=a$ and ${\Gamma }_{\mathcal{F}}\left(G\right)=b$.

Proof

If $a=1$, let $G=K_{1,b}$ and $\mathcal{F}=\left\{V\right\}$. Clearly, ${\gamma }_{\mathcal{F}}\left(G\right)=a=1$ and ${\Gamma }_{\mathcal{F}}\left(G\right)=b$.

Suppose $a\ge 2$. Let $G_1=K_a$ with $V\left(G_1\right)=\{u_1,u_2,\dots ,u_a\}$ and $G_2=K_{1,b-1}$ with $V\left(G_2\right)=\{u_1,v_1,v_2,\dots ,v_{b-1}\}$ and $E\left(G_2\right)=\{u_1{v}_1,u_1{v}_2,\dots ,u_1{v}_{b-1}\}$. Let $G=G_1\cup G_2$. Let $\mathcal{P}$ be a partition of $V(G_2-\left\{u_1\right\})$ into $a-1$ sets. Let $\mathcal{F}=\mathcal{P}\cup V\left(G_1\right)$. Since $\left|\mathcal{F}\right|=a$ and $\mathcal{F}$ is a partition of $V\left(G\right)$, it follows that ${\gamma }_{\mathcal{F}}\left(G\right)=a$. Now $S=\{v_1,v_2,\dots ,v_{b-1},u_2\}$ is a minimal $\mathcal{F}$-dominating set of $G$. Hence ${\Gamma }_{\mathcal{F}}\left(G\right)\ge \left|S\right|=b$. Let $A$ be any minimal $\mathcal{F}$-dominating set of $G$. If $\left|A\right|\ge b+1$, then $A$ contains at least two vertices of $G_1$. Hence $A$ is not a minimal $\mathcal{F}$-dominating set of $G$, which is a contradiction. Therefore ${\Gamma }_{\mathcal{F}}\left(G\right)\le b$. Hence ${\Gamma }_{\mathcal{F}}\left(G\right)=b$.

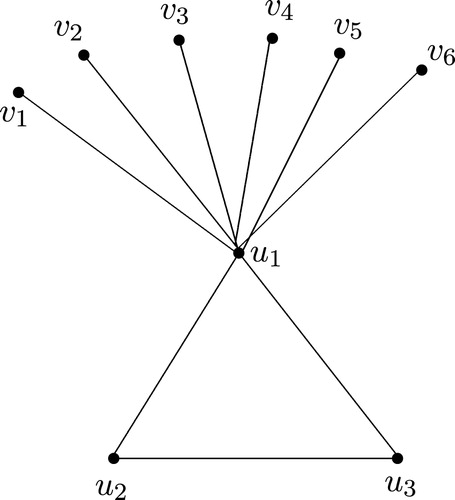
Example 3.4

An example of a graph with ${\gamma }_{\mathcal{F}}\left(G\right)=3$ and ${\Gamma }_{\mathcal{F}}\left(G\right)=7$ is given in Fig. 1. Let $F_1=\{v_1,v_2,v_3\},F_2=\{v_4,v_5,v_6\}$ and $F_3=\{u_1,u_2,u_3\}$. Let $\mathcal{F}=\{F_1,F_2,F_3\}.$ Then ${\gamma }_{\mathcal{F}}\left(G\right)=3$ and ${\Gamma }_{\mathcal{F}}\left(G\right)=7$.

Fig. 1 A graph $G$ with ${\gamma }_{\mathcal{F}}\left(G\right)=3$ and ${\Gamma }_{\mathcal{F}}\left(G\right)=7$.

As in the case of domination, we use the minimality condition of $\mathcal{F}$-dominating set for defining the concept of $\mathcal{F}$-irredundant sets.

Definition 3.5

Let $G=(V,E)$ be a graph and let $\mathcal{F}$ be a family of subsets of $V$ such that ${\bigcup }_{F\in \mathcal{F}}F=V.$ A subset $S$ of $V$ is called an $\mathcal{F}$-irredundant set if for every $v\in S$, one of the following conditions hold

(1) $pn[v,S]\ne \varphi$

(2) There exists $F\in \mathcal{F}$ such that $S\cap F=\left\{v\right\}$.

Theorem 3.6

An $\mathcal{F}$-dominating set $S$ is a minimal $\mathcal{F}$-dominating set if and only if it is $\mathcal{F}$-dominating and $\mathcal{F}$-irredundant.

Proof

It follows from the definition that any minimal $\mathcal{F}$-dominating set is $\mathcal{F}$-dominating and $\mathcal{F}$-irredundant. Conversely suppose that $S$ is $\mathcal{F}$-dominating and $\mathcal{F}$-irredundant. Let $v\in S$. If $pn[v,S]\ne \varphi$ then $S-\left\{v\right\}$ is not a dominating set of $G$. Also, if there exists $F\in \mathcal{F}$ such that $S\cap F=\left\{v\right\}$ then $(S-\left\{v\right\})\cap F=\varphi$. Hence $S-\left\{v\right\}$ is not an $\mathcal{F}$-dominating set. Hence $S$ is a minimal $\mathcal{F}$-dominating set.

It follows from the definition that any subset of an $\mathcal{F}$-irredundant set is also an $\mathcal{F}$-irredundant set. Hence $\mathcal{F}$-irredundance is a hereditary property. Thus an $\mathcal{F}$-irredundant set is maximal if and only if it is $1$-maximal. An $\mathcal{F}$-irredundant set $S$ is maximal, if and only if for every vertex $u\in V\left(G\right)-S$, $S\cup \left\{u\right\}$ is not an $\mathcal{F}$-irredundant set.

Theorem 3.7

Every minimal $\mathcal{F}$-dominating is maximal $\mathcal{F}$-irredundant.

Proof

Let S be a minimal $\mathcal{F}$-dominating set. Then it follows from Theorem 3.6 that $S$ is an $\mathcal{F}$-dominating set and an $\mathcal{F}$-irredundant set. Assume $S$ is not maximal $\mathcal{F}$-irredundant. Then by the 1-maximality condition, there exists a vertex $u\in V-S$ such that $S\cup \left\{u\right\}$ is $\mathcal{F}$-irredundant. Hence one of the following conditions hold.

1.	$pn[u,S\cup \left\{u\right\}]\ne \varphi$
2.	There exists $F\in \mathcal{F}$ such that $(S\cup \left\{u\right\})\cap F=\left\{u\right\}$.

Condition (1) implies that $u$ is not dominated by $S$ which is a contradiction.

Condition (2) implies that $S$ is not an $\mathcal{F}$-dominating set which is again a contradiction.

Hence if $S$ is minimal $\mathcal{F}$-dominating, then $S$ is maximal $\mathcal{F}$-irredundant.

Definition 3.8

The minimum cardinality of a maximal $\mathcal{F}$-irredundant set in $G$ is called the $\mathcal{F}$-irredundance number of $G$ and is denoted by $i{r}_{\mathcal{F}}\left(G\right)$. The maximum cardinality of an $\mathcal{F}$-irredundant set in $G$ is called the upper $\mathcal{F}$-irredundance number of $G$ and is denoted by $I{R}_{\mathcal{F}}\left(G\right)$.

Further it follows from Theorems 3.6 and 3.7 that $i{r}_{\mathcal{F}}\left(G\right)\le {\gamma }_{\mathcal{F}}\left(G\right)\le {\Gamma }_{\mathcal{F}}\left(G\right)\le I{R}_{\mathcal{F}}\left(G\right).$

4 Conclusion and scope

We have obtained an inequality chain of four parameters from $\mathcal{F}$-domination and $\mathcal{F}$-irredundance. To complete the chain analogous to the domination chain, we have to define the concept of $\mathcal{F}$-independence in such a way that it is a hereditary property and a $\mathcal{F}$-independent set is maximal if and only if it is $\mathcal{F}$-independent and $\mathcal{F}$-dominating. The formulation of such a definition is an open problem.