Dimension of a lobster

Abstract

A $k$-labeling of a graph is a labeling of vertices of the graph by $k$-tuples of non-negative integers in such a way that two vertices of $G$ are adjacent if and only if their label $k$-tuples differ in each coordinate. The dimension of a graph $G$ is the least $k$ such that $G$ has a $k$-labeling.

In this paper we obtain the dimension of a lobster or close bounds for it in various cases.

Keywords:

• Dimension of a graph
• Product dimension
• Lobster
• Caterpillar
• Graph labeling

1 Introduction

For a given graph $G$ (symmetric without loops), label the vertices by vectors of length $n$ with nonnegative integer coordinates in such a way that two vertices are joined by an edge if and only if the corresponding coordinates in their labeling are all different. Such a labeling is called a product representation of $G$. The least such $n$ is called the dimension of $G$. It is also the minimal number of complete graphs whose direct product (i.e. tensor product) contains $G$ as an induced subgraph. This dimension is denoted as $dim\left(G\right)$ or product dimension of $G$ or $\mathrm{pdim}\left(G\right)$ in the literature. Since $dim\left(G\right)$ is used in other contexts too, we shall use the notation $\mathrm{pdim}\left(G\right)$ in this paper.

A caterpillar is a graph which reduces to a path (called spine) after removing its pendent vertices. A lobster is a graph which reduces to a caterpillar after removing its pendent vertices. In this paper, we shall obtain dimension, or close upper and lower bounds for the dimension, for some classes of lobster.

Remark 1.1

A Criterion for Adjacent Vertices in Terms of an Inner Product Obtained from Labeling [1] Put $S\left(n\right)=\{A:A\subset \{1,2\dots ,n\}\}$.

Then $\left|S\left(n\right)\right|=2^n$. For a vector $x\in {\mathbb{N}}^n$ define vectors $\bar{x},\tilde{x}\in {\mathbf{N}}^{S\left(n\right)}$ by putting (1.1) $$\bar{x}\left(A\right)=\prod _{i\in A}{x}_{i}and\tilde{x}\left(A\right)=\prod _{i\notin A}(-x_i).$$(1.1) $\bar{x}$ and $\tilde{x}$ have $2^n$ coordinates corresponding to subsets $A\in S\left(n\right)$. Clearly (1.2) $$\prod _{i=1}^n(x_i-y_i)=\bar{x}.\tilde{y}$$(1.2) where the notation $\bar{x}.\tilde{y}$ designates the inner product of $\bar{x}$ and $\tilde{y}$.

In any product representation of a graph $G$, two vertices are adjacent if and only if their labels $x$ and $y$ satisfy $\bar{x}.\tilde{y}\ne 0$. This result will be used for getting a lower bound for the dimension of a lobster in Section 2.

For earlier results on the dimension of a path, cycle and caterpillar see [1–4].

2 A lower bound for the dimension of a lobster

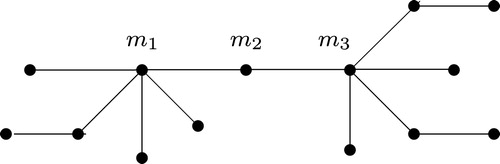
A lobster is a tree in which the removal of leaves (pendent vertices), leaves a caterpillar. Alternatively, consider stars $S_i$ with centers at $m_i$, $1\le i\le n$. Let $S_i^{\prime }$ be a graph obtained from $S_i$ in which some of the legs in $S_i$ may be further subdivided by a vertex. Next join $m_i$ to $m_{i+1}$, $1\le i\le n-1$. The resulting graph is called a Lobster. (See Fig. 1.)

Fig. 1 A lobster graph.

In this section and in Sections 3 and 4 we find bounds for dimension of a lobster and in certain cases, exact value of the dimension. Throughout this paper we denote by $L_n$ a lobster with a diametral path $P=(x^0,x^1,\dots \dots ,x^n)$. Obviously $P$ contains the spine of $L_n$.

Note 2.1

Let $L_n$ be a lobster with $deg\left(x^i\right)$ $\le 3$ where $2\le i\le n-2$. Let $B=\left\{i\right|2\le i\le n-2,deg\left(x^i\right)=3\}$. For $i\in B$, $x^i$ is called a leg vertex or a base-leg vertex. For $i\in B$, let $y^i$ be the vertex of $L_n$ of degree $2$ joined to $x^i$, and $z^i$ be the pendent vertex of $L_n$ joined to $y^i$. These three vertices form a leg (or path) of length $2$. Call $y^i$ a mid-leg vertex and $z^i$ a pendent-leg vertex of the lobster $L_n$. Thus the vertex set of $L_n$ is $$V=V\left(L_n\right)=\left\{x^i\right|0\le i\le n\}\cup \left\{y^i\right|i\in B\}\cup \left\{z^i\right|i\in B\}$$and the edge set of $L_n$ is $$E\left(L_n\right)=\left\{(x^i,x^{i+1})\right|0\le i\le n-1\}\cup \left\{(x^i,y^i)\right|i\in B\}\cup \left\{(y^i,z^i)\right|i\in B\}.$$ $x^0,x^n$ and $z^i$ for $i\in B$ are the pendent vertices of $L_n$. If $i\notin B$, $x^i$ is called a gap vertex or a non-leg vertex. Thus a leg vertex is of degree $3$ and a gap vertex $x^i$, $i\notin B$, is of degree $\le 2$.

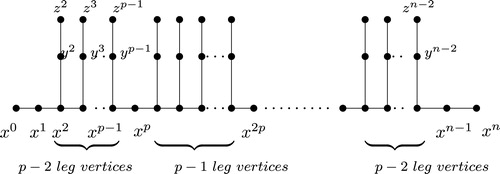
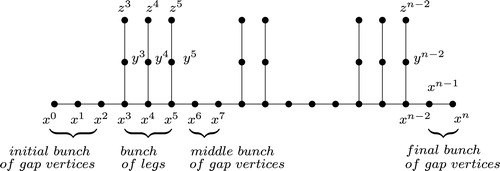
Let $x^{r+1},x^{r+2},\dots ,x^{r+t}$ be consecutive leg vertices of $L_n$ and suppose that $x^r$ and $x^{r+t+1}$ are gap vertices, i.e. $i\in B$ for $r+1\le i\le r+t$ but $r,r+t+1\notin B$. We call the induced subgraph on $x^i$, $y^i$ and $z^i$, $r+1\le i\le r+t$, a bunch of legs. The induced subgraph (path) on all gap vertices between consecutive bunches of legs is called a bunch of middle gap vertices. Note that, initial and final bunches of gap vertices in $L_n$ have at least two vertices each. Let $A=\left\{i\right|0\le i\le n\}$. From now on, our lobsters $L_n$ will have all the legs of length $2$.

Theorem 2.1

Let $L_n$, $n\ge 4$, be a lobster of length $n$ where $x^0,\dots ,x^n\in P$ and let $deg\left(x^i\right)$, $2\le i\le n-2$, be at most $3$. If all legs of the lobster are of length two and the initial and final bunches of non-leg vertices have at least two vertices, then $\mathrm{pdim}\left(L_n\right)$ satisfies the inequality,

$$\lceil {log}_2(\left|V\right|-1)\rceil \le \mathrm{pdim}\left(L_n\right).$$

Proof

Let $\mathrm{pdim}\left(L_n\right)=k$. Consider $L_n$ encoded in ${\mathbb{N}}^k$ by a product representation. For $(x_1,\dots ,x_k)$, $(y_1,\dots ,y_k)\in {\mathbb{N}}^k$, $$\prod _{i=1}^k(x_i-y_i)=\bar{x}.\tilde{y}$$where $\bar{x}$ and $\tilde{y}$ are $2^k$-tuples as defined in Eq. (1.1). For a vertex $x^i$, consider the $k$-tuple ${\mathbf{x}}^i=(x_1^i,x_2^i,\dots ,x_k^i)$ obtained by the embedding of $L_n$ in ${\mathbb{N}}^k$ and obtain $2^k$-tuples from this using (1.1). We denote these $2^k$-tuples for convenience by ${\bar{x}}^i$ and ${\tilde{x}}^i$. Similarly, we get ${\bar{y}}^i$ and ${\tilde{y}}^i$ from the vertex $y^i$ and ${\bar{z}}^i$ and ${\tilde{z}}^i$ from the vertex $z^i$. Now $(x^i,x^{i+1})\in E\left(L_n\right)$ for $i\in A$, and for $i\in B$, $(x^i,y^i),(y^i,z^i)\in E\left(L_n\right)$. As encodings of adjacent vertices agree in no coordinate, we get ${\bar{x}}^i.{\tilde{x}}^{i+1}={\prod }_{j=1}^k(x_j^i-x_j^{i+1})\ne 0$, and similarly for $i\in B$, ${\bar{x}}^i.{\tilde{y}}^i\ne 0$ and ${\bar{y}}^i.{\tilde{z}}^i\ne 0$. Also for $i,j\in A$, ${\bar{x}}^i.{\tilde{x}}^j=0$ if $|i-j|\ne 1$; for $i\in B$, ${\bar{x}}^i.{\tilde{z}}^i=0$ and for $i\in A$ and $j\in B$, ${\bar{x}}^i.{\tilde{y}}^j=0$, ${\bar{x}}^i.{\tilde{z}}^j=0$ if $i\ne j$, and also if $i,j\in B$, ${\bar{y}}^i.{\tilde{z}}^j=0$ for $i\ne j$, as encodings of non-adjacent vertices agree in at least one coordinate. We shall now show that the vectors in ${\mathbb{N}}^{S\left(k\right)}$ corresponding to the vertices $x^i$, $i\in A-\left\{0\right\}$ and $y^i$, $z^i$, $i\in B$, are $\mathbb{R}$-linearly independent, so that $\left|V\right|-1\le 2^k$. Let (2.1) $$\sum _{i\in A}{a}_i{\bar{x}}^i+\sum _{i\in B}{b}_i{\bar{y}}^i+\sum _{i\in B}{c}_i{\bar{z}}^i=0where{a}_i,b_i,c_i\in \mathbb{R}.$$(2.1)

We shall take the dot product of Eq. (2.1) with suitable ${\tilde{x}}^i$, ${\tilde{y}}^i$ and ${\tilde{z}}^i$ to show that $a_i=b_i=c_i=0$, for all $i$ appearing in (2.1). Take the dot product with ${\tilde{z}}^i$, $i\in B$, to get $b_i=0$ for $i\in B$. Now we consider the vertices $x^i$ ($i\ge 1$) of the diametral path $P$ one by one from $1\le i\le n$. Taking dot product with ${\tilde{x}}^{i-1}$, we get $a_i=0$ for $i\in A$. Now take the dot product with ${\tilde{y}}^i$, $i\in B$, to get $c_i=0$ for $i\in B$. (See Fig. 2.)

Thus, we get $\left|V\right|-1$ vectors in ${\mathbb{N}}^{S\left(k\right)}$ which are $\mathbb{R}$-linearly independent. Therefore $\left|V\right|-1\le 2^k$. Hence, $\lceil {log}_2(\left|V\right|-1)\rceil \le k=\mathrm{pdim}\left(L_n\right)$.

Fig. 2 The lobster in Theorem 2.1.

3 An upper bound for the dimension of a lobster

Theorem 3.1

Let $L_n$, $n\ge 4$, be a lobster of length $n$ and let $x^2,x^3,\dots ,$ $x^{n-2}$ be the vertices of the spine of $L_n$ with $deg\left(x^i\right)=3$ for $2\le i\le n-2$, $deg\left(x^i\right)=2$ for $i=1$, $n-1$ and $deg\left(x^i\right)=1$ for $i=0$, $n$. Let $(x^i,y^i,z^i)$ be a path of length $2$, which is the leg at $x^i$ for $2\le i\le n-2$. Then

$\mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2$.

Proof

To get the desired upper bound for $\mathrm{pdim}\left(L_n\right)$, we first show that the lobster $L_{2^k}$ can be embedded in ${\mathbb{N}}^{k+2}$. We consider the diametral path of $L_n$ given by $x^0$-$x^1$-$\cdots$-$x^n$. In analogy with a theorem of Lovász et al. ([1], Theorem 5.6), we define vectors $v_k\left(i\right)$, $u_k\left(i\right)$ and $w_k\left(i\right)$ corresponding to the vertices $x^i,y^i,z^i$ with $$v_k\left(i\right)\in K_3^{k+2},0\le i\le 2^k\text{and}{u}_k\left(i\right),w_k\left(i\right)\in K_3^{k+2},2\le i<2^k-2$$inductively as follows:

For $k=2$, define $v_2\left(i\right)$, $0\le i\le 4$, by $$v_2\left(0\right)=0000,v_2\left(1\right)=1111,v_2\left(2\right)=0022,v_2\left(3\right)=1110,v_2\left(4\right)=0001.$$

Again for $k=2$, define $u_2\left(i\right)$ and $w_2\left(i\right)$ for $i=2$, $u_2\left(2\right)=1201$, $w_2\left(2\right)=0010$.

Now for $k=3$, define $v_3\left(i\right)$, $0\le i\le 8$, by $$v_3\left(0\right)=00000,v_3\left(1\right)=11111,v_3\left(2\right)=00220,v_3\left(3\right)=11101,v_3\left(4\right)=00012,$$ $$v_3\left(5\right)=11100,v_3\left(6\right)=00221,v_3\left(7\right)=11110,v_3\left(8\right)=00001.$$

Again for $k=3$, define $u_3\left(i\right)$ and $w_3\left(i\right)$, $2\le i\le 6$, by $$u_3\left(2\right)=12011,u_3\left(3\right)=02210,u_3\left(4\right)=12201,u_3\left(5\right)=02211,u_3\left(6\right)=12000.$$ $$w_3\left(2\right)=00100,w_3\left(3\right)=10001,w_3\left(4\right)=00110,w_3\left(5\right)=10100,w_3\left(6\right)=00111.$$

For $k\ge 3$, we now define $v_k\left(i\right)$ for $0\le i\le 2^k$ by $$v^{\prime }\left(i\right)=\left\{\begin{array}{cc}0\hfill & \text{if}i\text{is even},\hfill \\ 1\hfill & \text{if}i\text{is odd},\hfill \end{array}\right.and{v}^{\prime \prime }\left(i\right)=\left\{\begin{array}{cc}1\hfill & \text{if}i\text{is even},\hfill \\ 0\hfill & \text{if}i\text{is odd}.\hfill \end{array}\right.$$ $$v_k\left(i\right)=\left\{\begin{array}{cc}{v}_{k-1}\left(i\right)v^{\prime }\left(i\right)\hfill & \text{if}0\le i<2^{k-1},\hfill \\ v_{k-1}\left(2^{k-1}\right)2\hfill & \text{if}i=2^{k-1},\hfill \\ v_{k-1}(2^k-i)v^{\prime \prime }\left(i\right)\hfill & \text{if}{2}^{k-1}+1\le i\le 2^k.\hfill \end{array}\right.$$

Again for $k\ge 3$, we define $u_k\left(i\right)$ and $w_k\left(i\right)$, $2\le i\le 2^k-2$, by

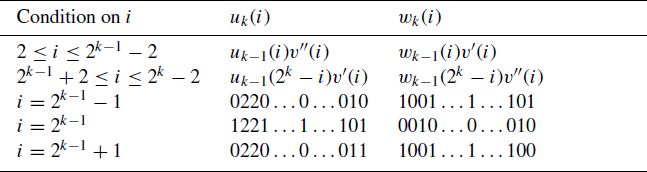
We see that the labeling works initially for $k=2$. When we go from $(k-1)$th stage of induction to $k$th stage, it is to be observed that we have essentially joined two $L_{2^{k-1}}$ to get an $L_{2^k}$; and in this process for $i=2^{k-1}-1,2^{k-1},2^{k-1}+1$, we initially have non-leg vertices which become leg-vertices in the $k$th step. Hence, these three vertices are to be treated somewhat differently. From the given formulas, we see that the adjacent vertices agree in no coordinates and the nonadjacent vertices either agree in the first $k+1$ coordinates coming from induction or agree in the (new) last coordinate. (See Fig. 3.)

This shows that the lobster $L_{2^k}$ can be embedded in ${\mathbb{N}}^{k+2}$ and $\mathrm{pdim}\left(L_{2^k}\right)\le k+2$. Now if $2^{k-1}<n\le 2^k$, then $L_n$ is an induced subgraph of $L_{2^k}$ and so $\mathrm{pdim}\left(L_n\right)\le \mathrm{pdim}\left(L_{2^k}\right)\le k+2=\lceil {log}_{2}n\rceil +2$. Hence, for any $n\ge 4$, $\mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2$.

Fig. 3 The Lobster in Theorem 3.1.

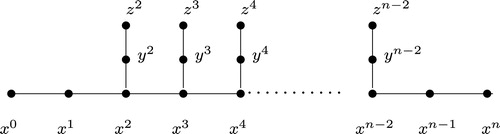
4 Dimension of a lobster

In this section we shall get upper and lower bounds for the dimension of a general lobster considered in Theorem 2.1. Then we consider two types of lobsters for which we get dimension for most $n$. In the lobsters considered in this section, for vertex $x^i\in P$ and having degree $3$, there is a leg $x^i$-$y^i$-$z^i$ associated with it, with $y^i$ as a mid-vertex and $z^i$ as a pendent vertex.

Theorem 4.1

Let $L_n$ be a lobster of diameter $n$ as considered in Theorem 2.1 . Then

$$\lceil {log}_2(n+2)\rceil \le \mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2.$$

Proof

In the notation of Theorem 2.1, there are $n+1$ $x^i$s and at least $1$ $y^i$ and $1$ $z^i$, so $\left|V\right|-1\ge n+1+1+1-1$. Thus $\left|V\right|-1\ge n+2$. Hence $\lceil {log}_2(n+2)\rceil \le \mathrm{pdim}\left(L_n\right)$.

Now $L_n$ is an induced subgraph of the lobster considered in Theorem 3.1. Hence $\mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2$.

Theorem 4.2

Let $L_n$, $n\ge 4$, be the lobster considered in Section 3 . Then

$$\lceil {log}_2\left(3(n-2)\right)\rceil \le \mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2.$$

In particular, if $\lceil {log}_{2}n\rceil =k$, then $k+1\le \mathrm{pdim}\left(L_n\right)\le k+2$.

Proof

In the notation of Theorem 2.1, there are $n+1$ $x^i$s, $n-3$ $y^i$s and $n-3$ $z^i$s, so $\left|V\right|-1=3n-6=3(n-2)$. Hence $\lceil {log}_2\left(3(n-2)\right)\rceil \le \mathrm{pdim}\left(L_n\right)$.

On the other hand, in Theorem 3.1 we proved that dimension $L_n$ satisfies $\mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2$. Hence, $\lceil {log}_2\left(3(n-2)\right)\rceil \le \mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2$.

Now let $\lceil {log}_{2}n\rceil =k$, so $2^{k-1}+1\le n\le 2^k$. Hence, $3(n-2)\ge 2^k+1$.

Theorem 4.3

Let $L_n$, $n\ge 4$, be the lobster considered in Theorem 4.2 . Let $k=\lceil {log}_{2}n\rceil$. The dimension of $L_n$ is given by

$$\mathrm{pdim}\left(L_n\right)=\lceil {log}_{2}n\rceil +2=k+2if{2}^{k-1}+2^{k-2}-\lfloor \frac{2^{k-2}}{3}\rfloor +2\le n\le 2^k.$$

For $2^{k-1}+1\le n<2^{k-1}+2^{k-2}-\lfloor \frac{2^{k-2}}{3}\rfloor +2$, $k+1\le \mathrm{pdim}\left(L_n\right)\le k+2$.

Proof

If $2^{k-1}+2^{k-2}-\lfloor \frac{2^{k-2}}{3}\rfloor +2\le n\le 2^k$, we show that, $\mathrm{pdim}\left(L_n\right)=k+2$. Let $m=2^{k-1}+2^{k-2}-\lfloor \frac{2^{k-2}}{3}\rfloor +2$, so $2(m-2)=2^k+2^{k-1}-2\lfloor \frac{2^{k-2}}{3}\rfloor$. Hence, $3(m-2)=2^k+2^{k-1}+2^{k-1}+2^{k-2}-3\lfloor \frac{2^{k-2}}{3}\rfloor$. Hence for some $t\in \{1,2\}$, $$3(m-2)=2^k+2^{k-1}+2^{k-1}+2^{k-2}-3\left(\frac{2^{k-2}-t}{3}\right)=2^{k+1}+t.$$

Now, by Theorem 4.2, $\lceil {log}_2\left(3(n-2)\right)\rceil \le \mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2$. So $$\text{for}m\le n\le 2^k,\lceil {log}_2(2^{k+1}+t)\rceil \le \mathrm{pdim}\left(L_n\right)\le \lceil {log}_2{2}^k\rceil +2.$$

Thus, $k+2\le \mathrm{pdim}\left(L_n\right)\le k+2$, so that, $\mathrm{pdim}\left(L_n\right)=k+2$.

Example 4.4

Take $k=10$. For $685\le n\le 1024$, $\mathrm{pdim}\left(L_n\right)=k+2=12$.

Let $p\ge 2$. Now we shall consider a lobster with sets of bunches with $p-1$ leg vertices followed by a gap vertex, except that for $p\ge 2$, initial and final bunches of leg vertices contain $p-2$ leg vertices.

Theorem 4.5

Let $p\ge 3$. Let $L_n$, $n\ge p+2$, be a lobster of length $n$ with $x^2,x^3,\dots ,x^{n-2}$ be the vertices of the spine of $L_n$ and let $deg\left(x^i\right)=3$ or $2$ according as $p\nmid i$ or $p|i$ for $2\le i\le n-2$. Let $n\equiv r(modp)$, $0\le r\le p-1$. Let $h=2$ if $r=1$ and $h=4$ if $r=0,2,3,\dots ,p-1$. The dimension of $L_n$ satisfies the inequality,

$$\lceil {log}_2(3n-2\lceil \frac{n}{p}\rceil -h)\rceil \le \mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2.$$

Let $k=\lceil {log}_{2}n\rceil$. In particular, for $n\ge 4$,

$$\text{for}{2}^k-\frac{(p-2)2^k}{3p-2}+2<n\le 2^k,\mathrm{pdim}\left(L_n\right)=k+2.$$

For $n\ge 6$, $k+1\le \mathrm{pdim}\left(L_n\right)\le k+2$.

For $n=5$, $p=\text{2,3}$, $\mathrm{pdim}\left(L_5\right)=k=3$.

For $n=6,7,8$, $\mathrm{pdim}\left(L_n\right)=k+1=4$. For $n=9,10,11,12$, $\mathrm{pdim}\left(L_n\right)=k+1=5$.

For $p=2$, $n\ge 5$, $\lceil {log}_2(n-2)\rceil +1\le \mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2$. (See Fig. 4 .)

Fig. 4 For the case $n=pr$.

Proof

Here $\left|V\right|-1=3n-2\lceil \frac{n}{p}\rceil -h$ where $h=2$ if $r=1$ and $h=4$ if $r=0,2,3,\dots ,p-1$. Therefore by Theorem 2.1, $\lceil {log}_2(3n-2\lceil \frac{n}{p}\rceil -h)\rceil \le \mathrm{pdim}\left(L_n\right)$, where $h=2$ if $r=1$ and $h=4$ if $r=0,2,3,\dots ,p-1$.

Now as $L_n$ is an induced subgraph of the lobster of Theorem 3.1, say $L_n^{\prime }$, we get $\mathrm{pdim}\left(L_n\right)\le \mathrm{pdim}\left(L_n^{\prime }\right)$. By Theorem 3.1, $\mathrm{pdim}\left(L_n^{\prime }\right)\le \lceil {log}_{2}n\rceil +2$. Thus, (∗) $$\lceil {log}_2(3n-2\lceil \frac{n}{p}\rceil -h)\rceil \le \mathrm{pdim}\left(L_n\right)\le \lceil {log}_{2}n\rceil +2.$$(∗)

Let $p\ge 3$. Take $k$ so that $2^{k-1}<n\le 2^k$. As $n\ge p+2$, we have $k\ge 3$. Thus $\mathrm{pdim}\left(L_n\right)\le k+2$. Now the lower and upper bounds in $(\ast )$ will be equal if $2^{k+1}<3n-2\lceil \frac{n}{p}\rceil -h$, i.e. $2^{k+1}<3n-2\frac{n+r^{\prime }}{p}-h$, where $r^{\prime }=p.\lceil \frac{n}{p}\rceil -n$ ($0\le r^{\prime }\le p-1$), i.e. $2^{k+1}<n\frac{3p-2}{p}-\frac{ph+2r^{\prime }}{p}$, i.e. $2^{k+1}\frac{p}{3p-2}+\frac{ph+2r^{\prime }}{3p-2}<n$, i.e. $2^k\frac{2p}{3p-2}+\frac{ph+2r^{\prime }}{3p-2}<n$, i.e. $2^k-\frac{p-2}{3p-2}{2}^k+\frac{ph+2r^{\prime }}{3p-2}<n$.

Further, $$\frac{ph+2r^{\prime }}{3p-2}\left\{\begin{array}{cc}=\frac{2p+2(p-1)}{3p-2}=1+\frac{p}{3p-2}\hfill & \text{if}r=1\text{,}h=2\text{,}{r}^{\prime }=p-1,\hfill \\ \le \frac{4p+2(p-2)}{3p-2}=2\hfill & \text{if}r\ne 1\text{,}h=4\text{,}0\le r^{\prime }\le p-2.\hfill \end{array}\right.$$Hence in any case we get equality for lower and upper bounds in $(\ast )$ if

$2^k-\frac{p-2}{3p-2}{2}^k+2<n\le 2^k$, and then $\mathrm{pdim}\left(L_n\right)=k+2$ for $k=3$, $5\le n\le 8$. Here $3\le p\le 6$, so $\frac{8}{7}\le \frac{p-2}{3p-2}{2}^k\le 2$. Hence for $k=3$, the condition $2^k-\frac{p-2}{3p-2}{2}^k+2<n\le 2^k$ is not satisfied. Hence we take $n\ge 4$.

Let $A=3n-2\lceil \frac{n}{p}\rceil -h=\left|V\right|-1$. Note that if $n$ is replaced by $n+1$, in the new lobster $L_{n+1}$, we have one additional vertex $x^{n+1}$. Also, at the vertex $x^{n-1}$, there will be two new vertices $y^{n-1}$, $z^{n-1}$ if and only if $p\nmid (n-1)$. Thus we get $1$ or $3$ new vertices if $n$ is replaced by $n+1$. Thus $A$ increases with $n$.

Let $p=3$ and $2^{k-1}+1\le n\le 2^k$. Now if $n=6$, then $A=10$. So $\lceil {log}_{2}A\rceil \ge 4=k+1$. Hence for $6\le n\le 8$, we have $k=3$, $A\ge 10$ and so $\lceil {log}_{2}A\rceil \ge 4=k+1$. For $n=9$, $k=4$, $A=17$, so $\lceil {log}_{2}A\rceil =5=k+1$ and for $n=10$, $A=20$, so $\lceil {log}_{2}A\rceil \ge 5=k+1$.

Now let $n\ge 11$, so $k\ge 4$. Hence $A\ge 3n-2\lceil \frac{n}{3}\rceil -4\ge 2n+n-2\lceil \frac{n}{3}\rceil -4\ge 2(2^{k-1}+1)+n-2\left(\frac{n+2}{3}\right)-4=2^k+\frac{n-10}{3}\ge 2^k+\frac{1}{3}$, so $\lceil {log}_{2}A\rceil \ge k+1$. Thus, for $n\ge 6$, $k+1\le \mathrm{pdim}\left(L_n\right)\le k+2$.

For $n=5$, $A=7$, so $\lceil {log}_{2}A\rceil =3=k\le \mathrm{pdim}\left(L_n\right)$. In fact $\mathrm{pdim}\left(L_n\right)=3$, as we can label $L_5$ by triplets as follows: $$v_3\left(0\right)=000,v_3\left(1\right)=111,v_3\left(2\right)=002,v_3\left(3\right)=120,v_3\left(4\right)=011,v_3\left(5\right)=102,$$ $$u_3\left(2\right)=012,w_3\left(2\right)=101.$$

For $6\le n\le 12$, $dim\left(L_n\right)\ge k+1$. By a similar labeling, we have checked that $\mathrm{pdim}\left(L_n\right)=k+1$ for these $n$, for $3\le p\le n-2$.

Now let $p=2$. Let $n\equiv r(mod2)$, $r=\text{0,1}$. Here, $\left|V\right|-1=3n-2\frac{n-r}{2}-4$. Thus, $\left|V\right|-1=2n-4$ for $n$ even, and $2n-3$ for $n$ odd. Hence, by Theorem 2.1, for $n$ even or odd, $\lceil {log}_2(n-2)\rceil +1\le \mathrm{pdim}\left(L_n\right)$.

Acknowledgment

The research of the second author was supported by research and development grant of Department.