?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
A hypergraph is said to be
-partite
-uniform if its vertex set
can be partitioned into non-empty sets
so that every edge in the edge set
, consists of precisely one vertex from each set
,
. It is denoted as
or
if
for
. In this paper we define
-partite self-complementary and almost self-complementary
-uniform hypergraph. We prove that, there exists an
-partite self-complementary
-uniform hypergraph
where
for
if and only if at least one of
is even. And we prove that, there exists an
-pasc
where
for
if and only if
are odd. Further, we analyze the cycle structure of complementing permutations of
-partite self-complementary
-uniform hypergraphs and
-partite almost self-complementary
-uniform hypergraphs.
1 Introduction
Let be a finite set with
vertices. By
we denote the set of all
-subsets of
. A
-uniform hypergraph is a pair
, where
.
is called a vertex set, and
an edge set of
. Two
-uniform hypergraphs
and
are isomorphic if there is a bijection
such that
induces a bijection of
onto
. If
is isomorphic to
, then
is called a self-complementary
-uniform hypergraph. Every permutation
which induces a bijection
is called a self-complementing permutation.
A. Symański, A. P. Wojda [Citation1–3] and S. Gosselin [Citation4], independently characterized and
for which there exist
-uniform self-complementary hypergraphs of order
and gave the structure of corresponding complementing permutations.
A -uniform hypergraph
is called almost self-complementary if it is isomorphic with
where
is an element of the set
. Almost self-complementary
-uniform hypergraph of order
may be called self-complementary in
. The almost self-complementary 2-uniform hypergraphs i.e. almost self-complementary graphs are introduced by Clapham in [Citation5]. In [Citation6], almost self-complementary
-uniform hypergraphs are considered. And in [Citation7], Wodja generalized corresponding results of [Citation5] for
and of [Citation6] for
for any
.
A hypergraph is said to be
-partite
-uniform [Citation8] if its vertex set
can be partitioned into non-empty sets
so that every edge in the edge set
, consists of precisely one vertex from each set
,
. It is denoted as
or
if
for
. An
-partite
-uniform hypergraph
with the vertex set
and the edge set
and
for
is called a complete
-partite
-uniform hypergraph. It is denoted as
or
. We observe that, the total number of edges in
is
. Given an
-partite
-uniform hypergraph
, we define its
-partite complement to be the
-partite
-uniform hypergraph
where
and
.
We say is the complement of
with respect to
. An
-partite
-uniform hypergraph
is said to be self-complementary if it is isomorphic to its
-partite complement
, that is there exists a bijection
such that
is an edge in
if and only if
is an edge in
.
T. Gangopadhyay and S. P. Rao Hebbare [Citation9] studied bi-partite self-complementary graphs, i.e. -partite self-complementary
-uniform hypergraphs (r
2). They characterized the structural properties of bi-partite complementing permutations. In the present paper we study
-partite self-complementary
-uniform hypergraphs and
-partite almost self-complementary
-uniform hypergraphs.
In Section 2, we prove the existence of -partite self-complementary
-uniform hypergraphs. In Section 3, we prove the existence of
-partite almost self-complementary
-uniform hypergraphs. In Sections 4 and 5 we analyze the cycle structure of complementing permutations of
-partite self-complementary
-uniform hypergraphs and the cycle structure of complementing permutations of
-partite almost self-complementary
-uniform hypergraphs respectively.
We use the shortform “-psc” for
-partite self-complementary
-uniform hypergraph.
2 Existence of 
 -partite self-complementary
-partite self-complementary 
 -uniform hypergraphs
-uniform hypergraphs
The concept of an -partite self-complementary
-uniform hypergraph with partition
of vertex set
can be interpreted as a partitioning of the edge set of
into two isomorphic factors. We note that a partitioning of the edge set of
into two isomorphic factors is possible only if
has an even number of edges i.e.
is even and this is true if and only if at least one of
is even. Conversely if we can construct an
-psc given that at least one
is even then we get a necessary and sufficient condition for existence of
-psc. Towards this we have the following theorem.
Theorem 2.1
There exists an -psc
where
for
if and only if at least one of
is even.
Proof
Firstly we construct an -psc
given that at least one of
is even. Without loss of generality, let us suppose that
is even. That is
for some positive integer
(say).
Let for
. Consider the complete
-partite
-uniform hypergraph,
.
Consider the following partition of edge set of .
is an edge in
and
is an edge in
and
.
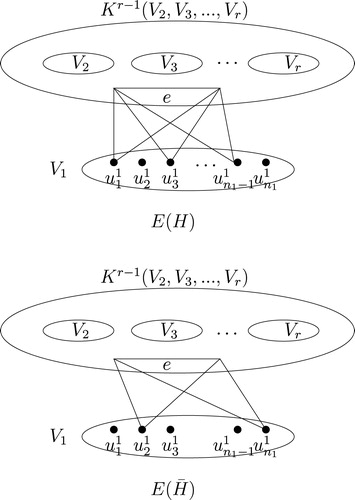
Let be the
-partite
-uniform hypergraph with edge set
. gives a diagrammatic description of
. To prove that
is
-psc, we define a bijection
as
. It can be easily checked that
is self-complementary with
as its complementing permutation.
It is clear that the partitioning of the edge set of into two isomorphic factors is not possible when
has an odd number of edges. In the next section we define an
-partite almost self-complementary
-uniform hypergraph and give a condition on number of vertices for its existence.
3 Existence of 
 -partite almost self-complementary
-partite almost self-complementary 
 -uniform hypergraphs
-uniform hypergraphs
Definition 3.1
Almost Complete -partite
-uniform Hypergraph The hypergraph
is called an almost complete
-partite
-uniform hypergraph where
is an edge in
called the deleted edge. Vertices of
will be called the special vertices.
Definition 3.2
Almost Self-complementary -partite
-uniform Hypergraph An
-partite
-uniform hypergraph
such that
for
is almost self-complementary if it is isomorphic with its complement
with respect to
.
We use the shortform “-pasc” for
-partite almost self-complementary
-uniform hypergraph.
A complete -partite
-uniform hypergraph will have an odd number of edges if each of
is odd. In the next theorem we prove that this condition is sufficient as well for the existence of an
-pasc. The proof is constructive in nature. Since the special vertices are to be treated differently and since each set in the partition contains exactly one special vertex, we start with
such that
contains even number of vertices for
. To construct
-pasc, we consider the complete
-partite
-uniform hypergraph on
and then add each vertex of
on each of these edges in such a way that we get the desired construction. The idea is the same as in the construction of Theorem 2.1.
Theorem 3.3
There exists an -pasc
where
for
if and only if
are odd.
Proof
We construct an -pasc
where
for
when each
is odd. Let
, for some positive integer
, for
.
Let and
, for
.
Consider the complete -partite
-uniform hypergraph
with edge set
.
Consider the following partition of the edge set of , where
is the deleted edge.
,
,
and
and
,
and
and
.
Now we have to consider edges containing special vertices along with
for
. For a given
, we have to consider all combinations of
special vertices
from
special vertices and remaining
vertices from
where
are distinct and belong to the set
.
Let . For
, let
and
. Note that for each
, there are
several
-subsets
. We consider all possible
-subsets.
For given , we divide the edges containing
special vertices along with
into two parts as follows.
Let,
and
.
and
.
Since . Hence the above partition is always a valid partition.
For given let,
and
.
Clearly, gives a partition of the edge set of
.
Let be the
-partite
-uniform hypergraph with edge set
. To prove
is
-pasc we define a bijection
such that
. It can be easily checked that
is almost self-complementary with
as its complementing permutation.
4 Complementing permutations of 
 -partite self-complementary
-partite self-complementary 
 -uniform hypergraphs
-uniform hypergraphs
Let be a partition of
. Any edge of
is a
-subset of
containing exactly one vertex from each of the partitioned sets
,
. Hence it is of the form
where
,
. If any
-subset of
contains more than one vertex from any one of the partitioned sets then we call it as an invalid edge. Hence any
-subset (r-tuple) of vertices in
is an invalid edge if and only if it contains at least two vertices from the same set of the partition. A permutation
on
is said to a complementing permutation of an
-psc
, if
is an edge in
whenever
is an edge in
. If
is a complementing permutation then the corresponding mapping induced on the set of edges of
is denoted by
.
Definition 4.1
Let be a partition of
. A permutation
is said to be a pure permutation on the set
if it is a permutation on the set
that can be written as a product of disjoint cycles containing all the vertices of
.
Definition 4.2
Let be a partition of
. A permutation
is said to be a mixed permutation on any
sets of
if it can be written as a product of disjoint cycles where each cycle contains at least one vertex from each of the
sets.
First we characterize those permutations on
for which
is an edge in
whenever
is an edge in
. We call such permutation as a valid permutation.
Lemma 4.3
Let be a partition of
and
be a valid permutation on
. If
is a cycle of
containing two consecutive vertices from a single set of the partition say
for some
then
must contain
where
is a pure permutation on
.
Proof
If is a
-cycle then we are done.
Let such that
.
Claim 1: .
Proof of 1: Suppose not. That is for at least one ,
. Choose that
for which
and
. This is possible since
is a cycle of
with
. Now
belong to different sets of the partition and hence any valid edge containing
and
will give
and
both belonging to
, thus giving an invalid edge, a contradiction to
is valid.
Claim 2: If there exists not belonging to the cycle
then
belongs to
where
is another cycle of
disjoint from
and contains vertices only from
.
Proof of claim 2: Let where at least one of the
(if any such exists) does not belong to
. Choose
such that
and
. Such a choice is possible since
and
is a cycle of
. Now any valid edge containing
from different sets will give an invalid edge containing
from some
, a contradiction to
is valid.
Hence contains
.
Lemma 4.4
Let be a partition of
and
be a valid permutation on
. If
is a cycle of
containing vertices from
then
(i) where
for all
and
.
(ii) must contain
where
is a mixed permutation on
.
Proof
Since is a cycle containing vertices from
, it must have length at least
and because of Lemma 4.3 no two consecutive vertices of
belong to the same set of the partition. The first
vertices of
must be one each from
in some order. If not that is suppose
such that
with
and
are not consecutive and
belong to different
’s for
then any valid edge containing
and
will give
and
both belonging to
, giving an invalid edge, a contradiction. Without loss of generality let
where
.
Claim 1: , for
where
for all
and
.
Proof of claim 1: Suppose not. Let and
be the smallest such that
. That is
for some
.
Case (i) Suppose . That is
. Then
for some
. That is
. We have
and
. Hence
and
belong to a valid edge but
and
both belong to
, a contradiction to
is valid.
Case (ii) Suppose .
.
Suppose , that is
. We have that
and
. Thus
and
belong to a valid edge whereas
and
both belong to
, a contradiction.
Suppose . We have
and
. Thus
and
belong to a valid edge but
and
both belong to
, which is a contradiction.
Hence length of must be multiple of
.
Claim 2: Every cycle of containing the vertices from
must be of the above type
with the same ordering of
.
Proof of claim 2: Suppose contains a cycle
containing vertices from
. Suppose for some
in
,
then for any edge
containing
in
and
,
is an invalid edge, a contradiction.
Claim 3: All the vertices of belong to cycles of type
.
Proof of claim 3: Suppose not. That is there is a cycle in
containing vertices from at least one of the sets
and vertices from
. Without loss, let us suppose that
contain vertices from
and
. Choose a vertex
where
from
such that
. Clearly,
and
in
belongs to
. Any valid edge
containing
and
gives
to be invalid, a contradiction.
Hence must contain
.
Further, for some
.
From Lemmas 4.3 and 4.4 we immediately get the following theorem which characterizes all valid permutations.
Theorem 4.5
(i) Any valid permutation on
is of the form
, where
is a mixed permutation on
for
such that
and
for
and
.
There cannot be a mixed permutation on
unless
, for some
.
The following remark gives a relation between the length of a cycle containing a particular edge in and the lengths of cycles in
containing the vertices of that edge where
is a valid permutation.
Remark 4.6
Let be any edge in
. Then the length of the cycle in
containing the edge
is the least common multiple of the lengths of cycles in
containing the vertices
except for the edge which contains
vertices
which belong to a cycle
of mixed permutation
on
sets (out of
) of length
such that
for
. For such an edge, length of the corresponding cycle in
depends on
instead of
. Further
will be a complementing permutation if and only if every cycle in the induced mapping
is of even length.
Following theorem gives the cycle structure of the complementing permutation of an -psc.
Theorem 4.7
A permutation is a complementing permutation of
-psc
if and only if following hold
(i) is valid, that is
, where
is a mixed permutation on
for
such that
and
for
and
.
(ii) either all the cycles in are of length even multiple of
for at least one
,
or all the cycles in
are of even length for at least one
,
.
Proof
Suppose is a complementing permutation of an
-psc
. Clearly,
must be valid. From Theorem 4.5, we have that
. For convenience we denote
by
.
Firstly we prove that for at least one ,
either all the cycles in
are of length even multiple of
or for at least one
,
all cycles in
are of even length.
Suppose not. That is for each ,
contains at least one cycle of length odd multiple of
and for each
,
contains at least one cycle of odd length. Let for each
,
be a cycle in
of length odd multiple of
and for
,
be a cycle in
of odd length. Let length of
be
where
is odd for
and length of
be
where
is odd for
. Let
and
.
Consider the edge,
in
. The length of the cycle of
containing the edge
is the least common multiple of
which is odd, a contradiction. Hence, either at least one
is even or at least one
is even. Therefore, either for at least one
,
all the cycles in
are of length even multiple of
or for at least one
,
all the cycles in
are of even length.
The following result proved by Gangopadhyay and S. P. Rao Hebbare [Citation9], on the cycle structure of the complementing permutations of a bipartite self-complementary graph (2-partite self-complementary 2-uniform hypergraphs) follows from Theorem 4.7.
Corollary 4.8
A permutation is a complementing permutation of bipartite self-complementary graph
if and only if either
(i) with all cycles in
or
are of even length or (ii)
and every cycle of
is of length a multiple of
and takes vertices alternately from
and
.
5 Complementing permutations of 
 -partite almost self-complementary
-partite almost self-complementary 
 -uniform hypergraphs
-uniform hypergraphs
Given an -pasc
, let the edges of
be colored red and the remaining edges of
be colored green. Since the 2 factors are isomorphic, there is a permutation
of the vertices of
that induces a mapping of the red edges onto the green edges. We consider
as a permutation of the vertices of
and denote by
the corresponding mapping induced on the set of edges of
. Thus
maps each red edge onto a green edge. However, the mapping
need not necessarily map each green edge onto a red edge. This would be so if
mapped
onto itself, but it may be that
maps
onto a red edge and some green edge onto e. Such a
(which, for definiteness we shall always assume induces a mapping from red to green) will (as for
-psc) be called a complementing permutation. It will be useful to consider the cycles of the induced mapping
.
For the rest of the section we denote the deleted edge by where
for
and call it as the missing edge. And the corresponding vertices
are called as the special vertices.
It is clear that the length of the cycle of containing the edge
must be odd and all the other cycles of
must be of even length.
If is any permutation on
, for
to be a complementing permutation it has to be valid and hence Theorem 4.5 holds. Remark 4.6 gives the relation between the lengths of cycles in
and
. In addition an extra requirement that exactly one cycle of
containing the deleted edge is of odd length and all the other cycles of
are of even length changes the cycle structure of complementing permutation of
-pasc from that of
-psc. And we have the following theorem.
Theorem 5.1
A permutation is a complementing permutation of
-pasc
if and only if
is valid, that is
where each
permutes vertices belonging to
number of sets of the partition
and
for
and
. Further, either
where
, where each
is a cycle of even length containing vertices from a single set of the partition. And for
,
, where each
is a valid mixed cycle of length even multiple of
containing vertices from
.
or
Among all the
’s,
, exactly one
say
is such that
where
is a cycle of odd length greater than 1 containing the vertex
and
is a cycle of even length containing vertices from
. Hence
where
where each
is a cycle of even length containing vertices from a single set of the partition. For each
,
is as in
.
or
Among all the
’s,
, exactly one
say
is such that
where
is a valid mixed cycle on
having length odd multiple
of
(
,
is even and
contains the special vertices
such that
and all other vertices from
. Each
is a valid mixed cycle on
of length even multiple of
. Hence
where for
,
is as in
and
is as in
.
Proof
Suppose is a complementing permutation of an
-pasc
. Clearly,
is valid. From Theorem 4.5, we have that
where
permutes vertices belonging to
,
permutes vertices belonging to
and so on
permutes vertices belonging to
and
for
and
. For convenience we denote
by
.
Consider the deleted edge, . We must have the length of the cycle of
containing
to be odd.
First we prove that all the special vertices belonging to any particular mixed permutation must belong to the same cycle, that is for each , the special vertices
belong to the same cycle of
.
Suppose not. That is suppose for some , the special vertices
do not belong to the same cycle of
. That is at least one vertex among these vertices belongs to a different cycle. Without loss, suppose the vertices
belong to a cycle
and the vertex
belongs to a cycle
of
of lengths
and
respectively. Clearly,
and
for some positive integers
and
. Note that both
and
must be odd. Since if either
or
is even then the cycle of
containing the edge
is of even length, a contradiction. Hence both
and
are odd. Further, since
and
there are vertices in
and
other than the special vertices which along with the remaining special vertices will form a valid edge and belong to a distinct cycle of
not containing
and at the same time having the same odd length as that of the cycle containing
, a contradiction. Hence, for each
, the special vertices
belong to the same cycle of
. Moreover, the length of this cycle is
, where
is odd.
Let be the cycle in
containing the special vertices
and having length
respectively for
, where each
is odd.
If is any other cycle in
for any
having length
then
must be even otherwise we will get a cycle of
of odd length not containing the edge
.
Let be the cycle in
of length
containing the special vertex
, for each
. Note that each
is odd. If not then, the cycle of
containing the edge
will be of even length, a contradiction.
If is any other cycle in
for any
then it must be of even length.
Observe that for any and
, at most one of
and
can be greater than 1. If not then we will get a cycle of
of odd length not containing
, a contradiction. Further,
(1) If for some ,
then
must be even with
and
for
.
(2) If for some ,
then for any vertex
in
, the cycle of
containing the special vertices other than
and
is of odd length which contains the edge
as well. And all the other cycles of
are of even length.
The cycle structure of complementing permutations of bipartite () almost self-complementary
-hypergraphs (graphs) can be obtained from Theorem 5.1 as stated in the following corollary.
Corollary 5.2
is a complementing permutation of
-pasc (bipartite almost self-complementary graph)
if and only if
is valid that is
or
where
permutes vertices belonging to
and
,
permute vertices belonging to
and
respectively. Further, either
where
and
have exactly one fixed special vertex
and
respectively, and all the other cycles of
and
are of even length.
or
where exactly one of
and
has exactly one cycle of odd length
containing the special vertex and the other has exactly one fixed special vertex. All the other cycles of
and
are of even length.
or
has a unique cycle of length
containing the special vertices
with
and all the other cycles are of length a multiple of
.
Acknowledgment
Authors wish to thank Professor N. S. Bhave for fruitful discussions.
References
- SzymańskiA., WojdaA.P., A note on k-uniform self-complementary hypergraphs of given order, Discuss. Math. Graph Theory, 29 2009 199–202
- SzymańskiA., WojdaA.P., Self-complementing permutations of k-uniform hypergraphs, Discrete Math. Theoret. Comput. Sci., 11 2009 117–124
- WojdaA., Self complementary hypergraphs, Discuss. Math. Graph Theory, 26 2006 217–224
- GosselinS., Constructing self-complementary uniform hypergraphs, Discrete Math., 310 2010 1366–1372
- ClaphamC.R.J., Graphs self-Complementary in Kn−e, Discrete Math., 81 1990 229–235
- KambleL.N., DeshpandeC.M., BamB.Y., Almost self-complementary 3-uniform hypergraphs, Discuss. Math. Graph Theory, 37 2017 131–140
- WojdaA., Almost self-complementary uniform hypergraphs, Discuss. Math. Graph Theory, 38 2018 607–610
- DiestelR., Graph Theory third ed. 2005Springer-Verlag
- T. Gangopadhyay, S.P. Rao Hebbare, Structural properties of r-partite complementing permutations, Tech. Report No. 19/77, I.S.I, Calcutta.