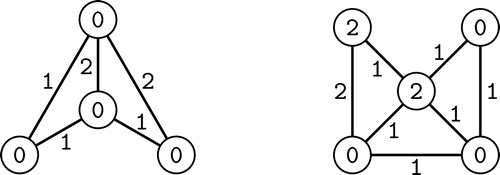Vertex irregular reflexive labeling of prisms and wheels

Abstract

For a graph $G$ we define $k$-labeling $\rho$ such that the edges of $G$ are labeled with integers $\{1,2,\dots ,k_e\}$ and the vertices of $G$ are labeled with even integers $\{0,2,\dots ,2k_v\}$, where $k=max\{k_e,2k_v\}$. The labeling $\rho$ is called a vertex irregular reflexive $k$-labeling if distinct vertices have distinct weights, where the vertex weight is defined as the sum of the label of that vertex and the labels of all edges incident this vertex. The smallest $k$ for which such labeling exists is called the reflexive vertex strength of $G$.

In this paper, we give exact values of reflexive vertex strength for prisms, wheels, fan graphs and baskets.

Keywords:

• Vertex irregular reflexive labeling
• Reflexive vertex strength
• Prism
• Wheel
• Fan graph

1 Introduction

All graphs considered in this article are connected, finite and undirected. A graph $G$ consists of a vertex set $V\left(G\right)$ and an edge set $E\left(G\right)$ or just $V$ and $E$ when the graph $G$ is clear. The graphs are also simple though they have their origin in multigraphs. In [1] the problem was posed “In a loopless multigraph, determine the fewest parallel edges required to ensure that all vertices have distinct degree”. In terms of simple graphs the problem becomes a graph labeling problem in which the number of parallel edges is represented as a positive integer on an edge and irregularity requires that the sum of all edge labels at vertices be pairwise distinct. The problem may be now expressed “assign positive values to the edges of a simply connected graph of order at least 3, in such a way that the graph becomes irregular. What is the minimum largest label over all such irregular assignments”? This minimum largest label is known as irregularity strength. Finding the irregularity strength of a graph seems to be hard even for graphs with simple structure, see [2–7].

Once the problem was considered as an edge labeling it is a simple step to pose it as a problem in total labeling in which both vertices and edges are labeled. This was first introduced by Bača et al. [8] where the authors defined vertex weight as the sum of all incident edge labels along with the label of the vertex. Now the problem is the same as in paragraph 1 except that the positive values are ascribed to both vertices and edges and we can remove the restriction of the graph being of order at least 3. The question remains one of finding the minimum largest label over all assignments. Such labeling is known as vertex irregular total $k$-labeling and total vertex irregularity strength of graph is the minimum $k$ for which the graph has a vertex irregular total $k$-labeling. The bounds for the total vertex irregularity strength given in [8] were then improved in [9,10] and recently by Majerski and Przybylo in [11].

In [12] the authors combined the total labeling problem with the original multigraph problem by identifying the vertex labels as representing loops. They referred to this labeling as an irregular reflexive labeling. This helped pose the problem in terms of real world networks but also had an effect on the vertex labels. Firstly, the vertex labels were required to be non-negative even integers (since each loop adds 2 to the vertex degree) and secondly, the vertex label 0 was permitted as representing a loopless vertex.

For a graph $G$ we define $k$-labeling $\rho$ such that the edges of $G$ are labeled with integers $\{1,2,\dots ,$ $k_e\}$ and the vertices of $G$ are labeled with even integers $\{0,2,\dots ,2k_v\}$, where $k=max\{k_e,2k_v\}$.

Specifically, under a total labeling $\rho$ the weight of a vertex $u$, denoted by $w{t}_{\rho }\left(u\right)$, is defined as $$w{t}_{\rho }\left(u\right)=\rho \left(u\right)+\sum _{uv\in E\left(G\right)}\rho \left(uv\right)$$while the weight of an edge $uv$, denoted by $w{t}_{\rho }\left(uv\right)$, is defined as $$w{t}_{\rho }\left(uv\right)=\rho \left(u\right)+\rho \left(v\right)+\rho \left(uv\right).$$

A labeling $\rho$ is said to be a vertex irregular reflexive $k$-labeling (resp. edge irregular reflexive $k$-labeling) if for $u,v\in V\left(G\right)$ is $w{t}_{\rho }\left(u\right)\ne w{t}_{\rho }\left(v\right)$ (resp. for $e,f\in E\left(G\right)$ is $w{t}_{\rho }\left(e\right)\ne w{t}_{\rho }\left(f\right)$). The smallest $k$ for which such labelings exist is called the reflexive vertex strength (resp. reflexive edge strength).

In this paper we provide exact values for the reflexive vertex strength for prisms, wheels, fans and baskets.

2 Vertex irregular reflexive labeling of prisms

Before we give the exact value of reflexive vertex strength for prisms we first prove one auxiliary lemma.

Lemma 1

The largest vertex weight of a graph $G$ of order $p$ and the minimum degree $\delta$ under any vertex irregular reflexive labeling is at least

1.	$p+\delta -1$ if $p\equiv 0(mod4)$, $p\equiv 1(mod4)$ and $\delta \equiv 0(mod2)$, or $p\equiv 3(mod4)$ and $\delta \equiv 1(mod2)$,
2.	$p+\delta$ otherwise.

Proof

Let $f$ be a vertex irregular reflexive labeling of a graph $G$ of order $p$ and the minimum degree $\delta$. Let us denote the vertices of $G$ by the symbols $v_1,v_2,\dots ,v_p$ such that $w{t}_f\left(v_i\right)<w{t}_f\left(v_{i+1}\right)$ for $i=1,2,\dots ,p-1$.

Then the vertex weight of a vertex $v_i$ is $$w{t}_f\left(v_i\right)=f\left(v_i\right)+\sum _{u{v}_i\in E\left(G\right)}f\left(u{v}_i\right)\ge 0+\sum _{u{v}_i\in E\left(G\right)}1\ge \delta .$$As the vertex weights are distinct we get $$w{t}_f\left(v_p\right)\ge w{t}_f\left(v_1\right)+p-1\ge p+\delta -1.$$Let us consider that $w{t}_f\left(v_p\right)=p+\delta -1$ which means that $$\{w{t}_f\left(v_i\right):i=1,2,\dots ,p\}=\{\delta ,\delta +1,\dots ,p+\delta -1\}.$$Thus the sum of all vertex weights is $$\sum _{i=1}^{p}w{t}_f\left(v_i\right)=\sum _{i=1}^p(\delta +i-1)=\frac{p(p+2\delta -1)}{2}.$$Evidently, this sum must be an even integer as $$\sum _{i=1}^{p}w{t}_f\left(v_i\right)=\sum _{i=1}^{p}f\left(v_i\right)+2\sum _{e\in E\left(G\right)}f\left(e\right),$$and every vertex label is even. Thus $$p(p+2\delta -1)\equiv 0(mod4),$$but it is not possible if $p\equiv 1(mod4)$ and $\delta \equiv 1(mod2)$, $p\equiv 2(mod4)$, or $p\equiv 3(mod4)$ and $\delta \equiv 0(mod2)$.

For regular graphs we immediately deduce the following corollary.

Corollary 1

Let $G$ be an $r$-regular graph of order $p$. Then $$\mathrm{rvs}\left(G\right)\ge \left\{\begin{array}{cc}⌈\frac{p+r-1}{r+1}⌉\hfill & \text{if}p\equiv 0,1(mod4)\text{,}\hfill \\ ⌈\frac{p+r}{r+1}⌉\hfill & \text{if}p\equiv 2,3(mod4)\text{.}\hfill \end{array}\right.$$

The prism $D_n$, $n\ge 3$, is a trivalent graph which can be defined as the Cartesian product $P_2\square C_n$ of a path on two vertices with a cycle on $n$ vertices. We denote the vertex set and the edge set of $D_n$ such that $V\left(D_n\right)=\{x_i,y_i:i=1,2,\dots ,n\}$ and $E\left(D_n\right)=\{x_i{x}_{i+1},y_i{y}_{i+1},x_i{y}_i:i=1,2,\dots ,n\}$, where indices are taken modulo $n$.

Theorem 1

For $n\ge 3$, $$\mathrm{rvs}\left(D_n\right)=⌈\frac{n}{2}⌉+1.$$

Proof

As the prism $D_n$ is a 3-regular graph of order $2n$, by Corollary 1 we obtain that $\mathrm{rvs}\left(D_n\right)\ge ⌈\frac{n}{2}⌉+1$.

We define the total labeling $f$ of $D_n$ in the following way $$f\left(x_i\right)=f\left(y_i\right)=0i=1,2,\dots ,⌈\frac{n}{2}⌉+1,$$$$f\left(x_i\right)=f\left(y_i\right)=⌈\frac{n}{2}⌉i=⌈\frac{n}{2}⌉+2,⌈\frac{n}{2}⌉+3,\dots ,n,\text{and}n\equiv 0,3(mod4),$$$$f\left(x_i\right)=f\left(y_i\right)=⌈\frac{n}{2}⌉+1i=⌈\frac{n}{2}⌉+2,⌈\frac{n}{2}⌉+3,\dots ,n,\text{and}n\equiv 1,2(mod4),$$$$f\left(x_i{x}_{i+1}\right)=1i=1,2,\dots ,n-1,$$$$f\left(x_1{x}_n\right)=1,$$$$f\left(y_i{y}_{i+1}\right)=⌈\frac{n}{2}⌉+1i=1,2,\dots ,n-1,$$$$f\left(y_1{y}_n\right)=⌈\frac{n}{2}⌉+1,$$$$f\left(x_i{y}_i\right)=ii=1,2,\dots ,⌈\frac{n}{2}⌉+1,$$$$f\left(x_i{y}_i\right)=i-⌈\frac{n}{2}⌉i=⌈\frac{n}{2}⌉+2,⌈\frac{n}{2}⌉+3,\dots ,n,\text{and}n\equiv 0,3(mod4),$$$$f\left(x_i{y}_i\right)=i-1-⌈\frac{n}{2}⌉i=⌈\frac{n}{2}⌉+2,⌈\frac{n}{2}⌉+3,\dots ,n,\text{and}n\equiv 1,2(mod4).$$Evidently $f$ is $\left(⌈\frac{n}{2}⌉+1\right)$-labeling and the vertices are labeled with even numbers.

For the vertex weights of the vertices $x_i$, $i=1,2,\dots ,⌈\frac{n}{2}⌉+1$ in $D_n$ under the labeling $f$ we have $$w{t}_f\left(x_i\right)=0+1+1+i=i+2.$$If $i=⌈\frac{n}{2}⌉+2,⌈\frac{n}{2}⌉+3,\dots ,n$ and $n\equiv 0,3(mod4)$ then $$w{t}_f\left(x_i\right)=⌈\frac{n}{2}⌉+1+1+\left(i-⌈\frac{n}{2}⌉\right)=i+2$$and for $i=⌈\frac{n}{2}⌉+2,⌈\frac{n}{2}⌉+3,\dots ,n$ and $n\equiv 1,2(mod4)$ $$w{t}_f\left(x_i\right)=\left(⌈\frac{n}{2}⌉+1\right)+1+1+\left(i-1-⌈\frac{n}{2}⌉\right)=i+2.$$Thus $\{w{t}_f\left(x_i\right):i=1,2,\dots ,n\}=\{3,4,\dots ,n+2\}$.

For the vertex weights of the vertices $y_i$, $i=1,2,\dots ,n$ in $D_n$ under the labeling $f$ we have the following $$w{t}_f\left(y_i\right)=0+\left(⌈\frac{n}{2}⌉+1\right)+\left(⌈\frac{n}{2}⌉+1\right)+i=i+2+2⌈\frac{n}{2}⌉\text{for}i=1,2,\dots ,⌈\frac{n}{2}⌉+1,$$$$w{t}_f\left(y_i\right)=⌈\frac{n}{2}⌉+\left(⌈\frac{n}{2}⌉+1\right)+\left(⌈\frac{n}{2}⌉+1\right)+\left(i-⌈\frac{n}{2}⌉\right)=i+2+2⌈\frac{n}{2}⌉\text{for}i=⌈\frac{n}{2}⌉+2,⌈\frac{n}{2}⌉+3,\dots ,n,\text{and}n\equiv 0,3(mod4),$$$$w{t}_f\left(y_i\right)=\left(⌈\frac{n}{2}⌉+1\right)+\left(⌈\frac{n}{2}⌉+1\right)+\left(⌈\frac{n}{2}⌉+1\right)+\left(i-1-⌈\frac{n}{2}⌉\right)=i+2+2⌈\frac{n}{2}⌉\text{for}i=⌈\frac{n}{2}⌉+2,⌈\frac{n}{2}⌉+3,\dots ,n,\text{and}n\equiv 1,2(mod4).$$Which means $$\{w{t}_f\left(y_i\right):i=1,2,\dots ,n\}=\{2⌈\frac{n}{2}⌉+3,2⌈\frac{n}{2}⌉+4,\dots ,n+2⌈\frac{n}{2}⌉+2\}=\left\{\begin{array}{c}\{n+3,n+4,\dots ,2n+2\}\text{for}n\text{even},\hfill \\ \{n+4,n+5,\dots ,2n+3\}\text{for}n\text{odd}.\hfill \end{array}\right.$$Thus the vertex weights are all distinct, that is $f$ is a vertex irregular reflexive $\left(⌈\frac{n}{2}⌉+1\right)$-labeling of a prism $D_n$.

3 Vertex irregular reflexive labeling of wheels

The wheel $W_n$, $n\ge 3$, is a graph obtained by joining all vertices of $C_n$ to a further vertex called the center. We denote the vertex set and the edge set of $W_n$ such that $V\left(W_n\right)=\{x,x_i:i=1,2,\dots ,n\}$ and $E\left(W_n\right)=\{x_i{x}_{i+1},x{x}_i:i=1,2,\dots ,n\}$, where indices are taken modulo $n$. The wheel is of order $n+1$ and size $2n$. We prove the following result for wheels.

Theorem 2

For $n\ge 3$, $$\mathrm{rvs}\left(W_n\right)=\left\{\begin{array}{cc}\lceil \frac{n+2}{4}\rceil \hfill & \text{if}n\not\equiv 2(mod8)\text{,}\hfill \\ \lceil \frac{n+2}{4}\rceil +1\hfill & \text{if}n\equiv 2(mod8)\text{.}\hfill \end{array}\right.$$

Proof

Let $n\ge 3$. As $\delta \left(W_n\right)=3$ then the smallest vertex weight is at least 3. The wheel $W_n$ contains $n$ vertices of degree 3 thus the largest weight over all vertices of degree 3 is at least $n+2$. Every vertex weight of a vertex of degree 3 is the sum of four labels from which at least one is even thus we have $$\mathrm{rvs}\left(W_n\right)\ge ⌈\frac{n+2}{4}⌉.$$However, if $n=8t+2$, $t\ge 1$, we get that the fraction $$⌈\frac{n+2}{4}⌉=⌈\frac{8t+4}{4}⌉=2t+1$$is odd. The number $n+2=8t+4$ can be realizable as the sum of four labels not greater than $2t+1$ only in the following way $$n+2=8t+4=(2t+1)+(2t+1)+(2t+1)+(2t+1),$$but this is a contradiction as the vertex label must be even. Thus, for $n\equiv 2(mod8)$ we obtain $$\mathrm{rvs}\left(W_n\right)\ge ⌈\frac{n+2}{4}⌉+1.$$Let $$R=\left\{\begin{array}{cc}\lceil \frac{n+2}{4}\rceil \hfill & \text{if}n\not\equiv 2(mod8)\text{,}\hfill \\ \lceil \frac{n+2}{4}\rceil +1\hfill & \text{if}n\equiv 2(mod8)\text{.}\hfill \end{array}\right.$$Let us denote by $K$ the largest even number not greater than $R$. Thus $$K=\left\{\begin{array}{cc}R\hfill & \text{if}n\equiv 2,3,4,5,6(mod8)\text{,}\hfill \\ R-1\hfill & \text{if}n\equiv 0,1,7(mod8)\text{.}\hfill \end{array}\right.$$

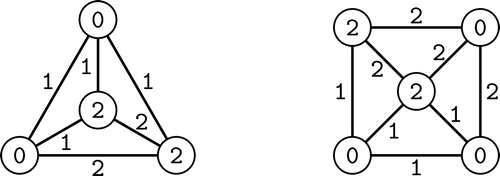
For $n=\text{3,4}$ we get that $\mathrm{rvs}\left(W_n\right)\ge 2$. The corresponding vertex irregular reflexive $2$-labelings for $W_3$ and $W_4$ are illustrated on Fig. 1.

For $n\ge 5$ we define the total $R$-labeling $f$ of $W_n$ such that $$f\left(x\right)=K,$$$$f\left(x_i\right)=0i=1,2,\dots ,2R+K-2,i\le n-1,$$$$f\left(x_i\right)=Ki=2R+K-1,2R+K,\dots ,n,$$$$f\left(x_{i}x\right)=⌈\frac{i}{3}⌉i=1,2,\dots ,2R+K-2,i\le n-1,$$$$f\left(x_{i}x\right)=i+3-2R-Ki=2R+K-1,2R+K,\dots ,n-1,$$$$f\left(x_{n}x\right)=R,$$$$f\left(x_i{x}_{i+1}\right)=⌈\frac{i-1}{3}⌉+1i=1,2,\dots ,2R+K-2,i\le n-1,$$$$f\left(x_i{x}_{i+1}\right)=Ri=2R+K-1,2R+K,\dots ,n-1,$$$$f\left(x_1{x}_n\right)=1.$$

For the weight of vertices of degree 3 under the labeling $f$ we obtain $$w{t}_f\left(x_1\right)=0+1+1+1=3,$$$$w{t}_f\left(x_i\right)=0+⌈\frac{i}{3}⌉+\left(⌈\frac{i-2}{3}⌉+1\right)+\left(⌈\frac{i-1}{3}⌉+1\right)=i+2\text{for}i=2,3,\dots ,2R+K-2,i\le n-1,$$$$w{t}_f\left(x_{2R+K-1}\right)=K+2+\left(⌈\frac{2R+K-3}{3}⌉+1\right)+R=2R+K+2,$$$$w{t}_f\left(x_i\right)=K+(i+3-2R-K)+R+R=i+3\text{for}i=2R+K,2R+K+1,\dots ,n-1,$$$$w{t}_f\left(x_n\right)=K+1+R+R=2R+K+1.$$It is easy to see that the weights of vertices $x_i$, $i=1,2,\dots ,n$, $n\ge 5$ and $n\ne 10$ are distinct numbers from the set $\{3,4,\dots ,n+2\}$. For $n=10$ we have $\{w{t}_f\left(x_i\right):i=1,2,\dots ,10\}=\{3,4,\dots ,11,13\}$.

The weight of the vertex $x$ is $$w{t}_f\left(x\right)=f\left(x\right)+\sum _{i=1}^{n}f\left(x_{i}x\right)=K+\sum _{i=1}^{n}f\left(x_{i}x\right)=K+R+\sum _{i=1}^{n-1}f\left(x_{i}x\right)>K+R+n-1.$$Evidently, for $n\ge 5$, the vertex weights are distinct.

Fig. 1 The vertex irregular reflexive $2$-labelings of wheels $W_3$ and $W_4$.

A fan graph $F_n$ is obtained from wheel $W_n$ if one rim edge, say $x_1{x}_n$ is deleted. A basket $B_n$ is obtained by removing a spoke, say $x{x}_n$, from wheel $W_n$. Before we will give the exact value of reflexive vertex strength of fans and baskets we give the following observation.

Observation 1

Let $f$ be a vertex irregular reflexive $k$-labeling of a graph $G$. If there exists an edge $uv$ in $G$ such that $$w{t}_f\left(u\right)-f\left(uv\right)\notin \{w{t}_f\left(x\right):x\in V\left(G\right)-\left\{v\right\}\},$$$$w{t}_f\left(v\right)-f\left(uv\right)\notin \{w{t}_f\left(x\right):x\in V\left(G\right)-\left\{u\right\}\}$$then $f$ is a vertex irregular reflexive $k$-labeling of a graph $G-\left\{uv\right\}$.

Proof

The proof is trivial.

Immediately from this observation we get the following corollary.

Corollary 2

Let $\mathrm{rvs}\left(G\right)=k$ and let $f$ be the corresponding vertex irregular reflexive $k$-labeling of a graph $G$. If the vertex weights of vertices $u,v$ are the smallest over all vertex weights under the labeling $f$ and $uv\in E\left(G\right)$ then $$\mathrm{rvs}(G-\left\{uv\right\})\le \mathrm{rvs}\left(G\right).$$

Proof

Let $f$ be a vertex irregular reflexive $k$-labeling of a graph $G$. Let $u$, $v$ be two adjacent vertices and let the vertex weights of these vertices be the smallest over all vertices in $G$. Without loss of generality assume $w{t}_f\left(u\right)<w{t}_f\left(v\right)$. This means that for every $w\in V\left(G\right)-\{u,v\}$, (1) $$w{t}_f\left(u\right)<w{t}_f\left(v\right)<w{t}_f\left(w\right).$$(1) Let $g$ be the restriction of the labeling $f$ on $G-\left\{uv\right\}$. Evidently $$w{t}_g\left(u\right)=w{t}_f\left(u\right)-f\left(uv\right),$$$$w{t}_g\left(v\right)=w{t}_f\left(v\right)-f\left(uv\right),$$$$w{t}_g\left(w\right)=w{t}_f\left(w\right)\text{for every}w\in V\left(G\right)-\{u,v\}\text{.}$$Combining with (1) we obtain $$w{t}_g\left(u\right)=w{t}_f\left(u\right)-f\left(uv\right)<w{t}_f\left(v\right)-f\left(uv\right)=w{t}_g\left(v\right)<w{t}_f\left(w\right)=w{t}_g\left(w\right).$$Thus, immediately using Observation 1 we have $\mathrm{rvs}(G-\left\{uv\right\})\le \mathrm{rvs}\left(G\right)$.

For the fan graph $F_n$ we prove

Theorem 3

For $n\ge 3$, $$\mathrm{rvs}\left(F_n\right)=\left\{\begin{array}{cc}\lceil \frac{n+1}{4}\rceil \hfill & \text{if}n\not\equiv 3(mod8)\text{,}\hfill \\ \lceil \frac{n+1}{4}\rceil +1\hfill & \text{if}n\equiv 3(mod8)\text{.}\hfill \end{array}\right.$$

Proof

The fan graph $F_n$ contains two vertices of degree 2, thus the smallest vertex weight is at least 2. The fan graph $F_n$ contains $n-2$ vertices of degree 3, thus the largest weight of a vertex of degree 3 is at least $n$.

If all vertex weights of vertices of degree 3 are at most $n$, then one of the vertices of degree 2 has to have weight at least $n+1$ and thus $\mathrm{rvs}\left(F_n\right)\ge \lceil \frac{n+1}{3}\rceil$. If a vertex of degree 3 has weight greater than $n$ then $\mathrm{rvs}\left(F_n\right)\ge \lceil \frac{n+1}{4}\rceil$. As we are trying to minimize the parameter $k$ for which there exists vertex irregular reflexive $k$-labeling of $F_n$ we obtain $$\mathrm{rvs}\left(F_n\right)\ge \lceil \frac{n+1}{4}\rceil ,$$which can be obtained when both vertices of degree 2 in $F_n$ will have weights less than $n$.

According to the proof of Theorem 2 and Corollary 2, for $n\ge 5$, we get $$\mathrm{rvs}\left(F_n\right)\le \mathrm{rvs}\left(W_n\right)=\left\{\begin{array}{cc}\lceil \frac{n+2}{4}\rceil \hfill & \text{if}n\not\equiv 2(mod8)\text{,}\hfill \\ \lceil \frac{n+2}{4}\rceil +1\hfill & \text{if}n\equiv 2(mod8)\text{.}\hfill \end{array}\right.$$Moreover, we can derive a vertex irregular reflexive $\mathrm{rvs}\left(W_n\right)$-labeling of $F_n$ from a vertex irregular reflexive $\mathrm{rvs}\left(W_n\right)$-labeling of $W_n$.

Combining the previous facts we have that for $n\not\equiv 2,3,7(mod8)$ $$\mathrm{rvs}\left(F_n\right)=\lceil \frac{n+1}{4}\rceil$$and for $n\equiv 2,3,7(mod8)$ $$\lceil \frac{n+1}{4}\rceil \le \mathrm{rvs}\left(F_n\right)\le \lceil \frac{n+1}{4}\rceil +1.$$

For $n=\text{3,4}$ we get that $\mathrm{rvs}\left(F_n\right)\ge 2$. The corresponding vertex irregular reflexive $2$-labelings for $F_3$ and $F_4$ are illustrated on Fig. 2.

Let $n=8t+3$, $t\ge 1$, then $\lceil \frac{n+1}{4}\rceil =2t+1$. As this value is odd we cannot get the number $n+1=8t+4$ as the sum of four labels less or equal to $2t+1$ from which at least one is even. Thus $\mathrm{rvs}\left(F_n\right)=\lceil \frac{n+1}{4}\rceil +1$ but in this case $$\mathrm{rvs}\left(W_n\right)=\lceil \frac{n+2}{4}\rceil =\lceil \frac{n+1}{4}\rceil +1$$and we are done.

We denote the vertex set and the edge set of $F_n$ such that $V\left(F_n\right)=\{x,x_i:i=1,2,\dots ,n\}$ and $E\left(F_n\right)=\{x_i{x}_{i+1}:i=1,2,\dots ,n-1\}\cup \{x{x}_i:i=1,2,\dots ,n\}$.

If $n=8t+2$, $t\ge 1$ then $\lceil \frac{n+1}{4}\rceil =2t+1$. We define a $(2t+1)$-labeling of $F_n$ such that $$f\left(x\right)=2t,$$$$f\left(x_i\right)=0i=1,2,\dots ,6t,$$$$f\left(x_i\right)=2ti=6t+1,6t+2,\dots ,8t+2,$$$$f\left(x_{1}x\right)=1,$$$$f\left(x_{i}x\right)=⌈\frac{i-1}{3}⌉i=2,3,\dots ,6t,$$$$f\left(x_{i}x\right)=i-6ti=6t+1,6t+2,\dots ,8t+1,$$$$f\left(x_{8t+2}x\right)=2t+1,$$$$f\left(x_i{x}_{i+1}\right)=⌈\frac{i-2}{3}⌉+1i=1,2,\dots ,6t,$$$$f\left(x_i{x}_{i+1}\right)=2t+1i=6t+1,6t+2,\dots ,8t+1.$$It is easy to verify that the set of all vertex weights is $\{2,3,\dots ,8t+3,8t^2+8t+3\}$.

If $n=8t+7$, $t\ge 0$ then $\lceil \frac{n+1}{4}\rceil =2t+2$. We define $(2t+2)$-labeling of $F_n$ in the following way $$f\left(x\right)=2t+2,$$$$f\left(x_i\right)=0i=1,2,\dots ,6t+4,$$$$f\left(x_i\right)=2t+2i=6t+5,6t+6,\dots ,8t+7,$$$$f\left(x_{1}x\right)=1,$$$$f\left(x_{i}x\right)=⌈\frac{i-1}{3}⌉i=2,3,\dots ,6t+4,$$$$f\left(x_{i}x\right)=i-6t-4i=6t+5,6t+6,\dots ,8t+6,$$$$f\left(x_{8t+7}x\right)=2t+2,$$$$f\left(x_i{x}_{i+1}\right)=⌈\frac{i-2}{3}⌉+1i=1,2,\dots ,6t+4,$$$$f\left(x_i{x}_{i+1}\right)=2t+2i=6t+5,6t+6,\dots ,8t+6.$$Evidently the vertex weights are distinct.

Fig. 2 The vertex irregular reflexive $2$-labelings of fans $F_3$ and $F_4$.

Theorem 4

For $n\ge 3$, $$\mathrm{rvs}\left(B_n\right)=\left\{\begin{array}{cc}\lceil \frac{n+1}{4}\rceil \hfill & \text{if}n\not\equiv 3(mod8)\text{,}\hfill \\ \lceil \frac{n+1}{4}\rceil +1\hfill & \text{if}n\equiv 3(mod8)\text{.}\hfill \end{array}\right.$$

Proof

The basket $B_n$ contains one vertex of degree 2, therefore the smallest vertex weight is at least 2 and it contains $n-1$ vertices of degree 3, hence the largest weight of a vertex of degree 3 is at least $n+1$. Thus $$\mathrm{rvs}\left(B_n\right)\ge \lceil \frac{n+1}{4}\rceil .$$Analogously as in the proof of the previous theorem, using Theorem 2 and Observation 1, for $n\ge 5$, we have $$\mathrm{rvs}\left(B_n\right)\le \mathrm{rvs}\left(W_n\right)=\left\{\begin{array}{cc}\lceil \frac{n+2}{4}\rceil \hfill & \text{if}n\not\equiv 2(mod8)\text{,}\hfill \\ \lceil \frac{n+2}{4}\rceil +1\hfill & \text{if}n\equiv 2(mod8)\text{.}\hfill \end{array}\right.$$Moreover, we can derive a vertex irregular reflexive $\mathrm{rvs}\left(W_n\right)$-labeling of $B_n$ from the vertex irregular reflexive $\mathrm{rvs}\left(W_n\right)$-labeling of $W_n$ defined in the proof of Theorem 2 by deleting the spoke $x_{1}x$ in $W_n$.

Combining the previous facts we get that for $n\not\equiv 2,3,7(mod8)$ $$\mathrm{rvs}\left(B_n\right)=\lceil \frac{n+1}{4}\rceil$$and $n\equiv 2,3,7(mod8)$ $$\lceil \frac{n+1}{4}\rceil \le \mathrm{rvs}\left(B_n\right)\le \lceil \frac{n+1}{4}\rceil +1.$$

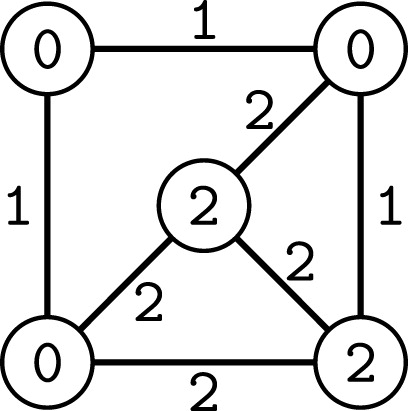
For $n=\text{3,4}$ we get that $\mathrm{rvs}\left(B_n\right)\ge 2$. The basket $B_3$ is isomorphic to the fan $F_3$. The vertex irregular reflexive $2$-labelings for $B_4$ is illustrated on Fig. 3.

Let $n=8t+3$, $t\ge 1$, then $\lceil \frac{n+1}{4}\rceil =2t+1$. As this is odd we cannot get the number $n+1=8t+4$ as the sum of four labels less or equal to $2t+1$ from which at least one is even. Thus $\mathrm{rvs}\left(B_n\right)=\lceil \frac{n+1}{4}\rceil +1$ but in this case $$\mathrm{rvs}\left(W_n\right)=\lceil \frac{n+2}{4}\rceil +1=\lceil \frac{n+1}{4}\rceil +1$$and we are done.

Let us denote the vertex set and the edge set of the basket $B_n$ such that $V\left(B_n\right)=\{x,x_i:i=1,2,\dots ,n\}$ and $E\left(B_n\right)=\{x{x}_i:i=2,3,\dots ,n\}\cup \{x_i{x}_{i+1}:i=1,2,\dots ,n-1\}\cup \left\{x_n{x}_1\right\}$.

If $n=8t+2$, $t\ge 1$ then $\lceil \frac{n+1}{4}\rceil =2t+1$. We define $(2t+1)$-labeling of $B_n$ such that $$f\left(x\right)=2t,$$$$f\left(x_i\right)=0i=1,2,\dots ,6t+1,$$$$f\left(x_i\right)=2ti=6t+2,6t+3,\dots ,8t+2,$$$$f\left(x_{i}x\right)=⌈\frac{i-1}{3}⌉i=2,3,\dots ,6t+1,$$$$f\left(x_{i}x\right)=i-6ti=6t+2,6t+3,\dots ,8t+1,$$$$f\left(x_{8t+2}x\right)=2t+1,$$$$f\left(x_i{x}_{i+1}\right)=⌈\frac{i-2}{3}⌉+1i=1,2,\dots ,6t,$$$$f\left(x_i{x}_{i+1}\right)=2t+1i=6t+1,6t+2,\dots ,8t+1,$$$$f\left(x_1{x}_{8t+2}\right)=1.$$

If $n=8t+7$, $t\ge 0$ then $\lceil \frac{n+1}{4}\rceil =2t+2$. We define $(2t+2)$-labeling of $B_n$ in the following way $$f\left(x\right)=2t+2,$$$$f\left(x_i\right)=0i=1,2,\dots ,6t+5,$$$$f\left(x_i\right)=2t+2i=6t+6,6t+7,\dots ,8t+7,$$$$f\left(x_{i}x\right)=⌈\frac{i-1}{3}⌉i=2,3,\dots ,6t+5,$$$$f\left(x_{i}x\right)=i-6t-4i=6t+6,6t+7,\dots ,8t+6,$$$$f\left(x_{8t+7}x\right)=2t+2,$$$$f\left(x_i{x}_{i+1}\right)=⌈\frac{i-2}{3}⌉+1i=1,2,\dots ,6t+5,$$$$f\left(x_i{x}_{i+1}\right)=2t+2i=6t+6,6t+7,\dots ,8t+6,$$$$f\left(x_1{x}_{8t+7}\right)=1.$$

It is not difficult to show that in both cases the described labelings have desired properties.

Fig. 3 The vertex irregular reflexive $2$-labeling of basket $B_4$.

4 Conclusion

In this paper we determined exact values of the reflexive vertex strength for prisms $D_n$, wheels $W_n$, fan graphs $F_n$ and for baskets $B_n$, $n\ge 3$.

Acknowledgments

This work was supported by the Slovak Science and Technology Assistance Agency, Slovak Republic under the contract no. APVV-15-0116 and by VEGA, Slovak Republic 1/0233/18.