The distinguishing number and the distinguishing index of line and graphoidal graph(s)

Abstract

The distinguishing number (index) $D\left(G\right)$ ($D^{\prime }\left(G\right)$) of a graph $G$ is the least integer $d$ such that $G$ has a vertex labeling (edge labeling) with $d$ labels that is preserved only by a trivial automorphism. A graphoidal cover of $G$ is a collection $\psi$ of (not necessarily open) paths in $G$ such that every path in $\psi$ has at least two vertices, every vertex of $G$ is an internal vertex of at most one path in $\psi$ and every edge of $G$ is in exactly one path in $\psi$. Let $\Omega (G,\psi )$ denote the intersection graph of $\psi$. A graph $H$ is called a graphoidal graph, if there exist a graph $G$ and a graphoidal cover $\psi$ of $G$ such that $H\cong \Omega (G,\psi )$. In this paper, we study the distinguishing number and the distinguishing index of the line graph and the graphoidal graph of a simple connected graph $G$.

Keywords:

• Distinguishing number
• Distinguishing index
• Line and graphoidal graph(s)

1 Introduction and definitions

Let $G=(V,E)$ be a simple, finite, connected and undirected graph, and let $\mathrm{Aut}\left(G\right)$ be its automorphism group.A labeling of $G$, $\varphi :V\to \{1,2,\dots ,r\}$, is said to be $r$-distinguishing, if no non-trivial automorphism of $G$ preserves all of the vertex labels. The point of the labels on the vertices is to destroy the symmetries of the graph, that is, to make the automorphism group of the labeled graph trivial. Formally, $\varphi$ is $r$-distinguishing if for every non-identity $\sigma \in \mathrm{Aut}\left(G\right)$, there exists $x$ in $V$ such that $\varphi \left(x\right)\ne \varphi \left(\sigma \left(x\right)\right)$. The distinguishing number of a graph $G$ is defined by $$D\left(G\right)=min\left\{r\right|G\text{has a labeling that is}r\text{-distinguishing}\}.$$

This number was defined in [1]. Similar to this definition, in [2] the distinguishing index $D^{\prime }\left(G\right)$ of $G$, which is the least integer $d$ such that $G$ has an edge coloring with $d$ colors that is preserved only by a trivial automorphism, has been defined. $D^{\prime }\left(G\right)$ can be arbitrary smaller than $D\left(G\right)$, for example $D^{\prime }\left(K_{p,p}\right)=2$ and $D\left(K_{p,p}\right)=p+1$, for $p\ge 4$.

The line graph $L\left(G\right)$ of a graph $G$ is the graph whose vertices are edges of $G$ and two edges $e,e^{\prime }\in V\left(L\left(G\right)\right)=E\left(G\right)$ are adjacent if they share an endpoint. The line graphs can be viewed a special case of graphoidal graphs. The concept of graphoidal cover was introduced by Acharya and Sampathkumar [3].

Definition 1.1

[3] A graphoidal cover of a graph $G$ is a collection $\psi$ of (not necessarily open) paths in $G$ satisfying the following conditions:

(i)	Every path in $\psi$ has at least two vertices.
(ii)	Every vertex of $G$ is an internal vertex of at most one path in $\psi$.
(iii)	Every edge of $G$ is in exactly one path in $\psi$.

Definition 1.2

[3] If $F=\{S_1,S_2,\dots ,S_n\}$ is a family of distinct nonempty subsets of a set $S$, whose union is $S$, then the intersection graph of $F$, denoted by $\Omega \left(F\right)$, is the graph whose vertex set and edge set are given by $$V\left(F\right)=\{S_1,S_2,\dots ,S_n\},E\left(F\right)=\{S_i{S}_j:i\ne j,S_i\cap S_j\ne \varnothing \}.$$

Let ${\mathcal{G}}_G$ be the set of all graphoidal covers of $G$ and $\psi \in {\mathcal{G}}_G$. The intersection graph on $\psi$ is denoted by $\Omega (G,\psi )$. A graph $H$ is called a graphoidal graph if there exist a graph $G$ and $\psi \in {\mathcal{G}}_G$ such that $H\cong \Omega (G,\psi )$. Since $E\left(G\right)$ is obviously a graphoidal cover of $G$, all line graphs are graphoidal graphs. In [3] Acharya and Sampathkumar have proved that all the Beineke’s forbidden subgraphs of line graphs (see Fig. 1) are graphoidal graphs and hence they conjectured that all graphs are graphoidal. In [4] Arumugam and Pakkiam disproved this conjecture by showing that complete bipartite graphs $K_{m,n}$ with $mn>2(m+n)$ are not graphoidal graphs. They also obtained a forbidden subgraph characterization of all bipartite graphs which are graphoidal. Note that if $P=(v_0,v_1,\dots ,v_k)$ is a path, not necessarily open, in a graph $G$, then $v_0$ and $v_k$ are called terminal vertices and $v_1,\dots ,v_{k-1}$ are called internal vertices of $P$. For cycles (considered as closed paths), there is an inherent “ordering” of vertices as in paths. So, when we say that a cycle $C$ of a graph $G$ is a member of a graphoidal cover $\psi$ of $G$, we should mention the vertex at which the cycle $C$ begins, and this particular vertex is considered as the terminal vertex of $C$ and all other vertices on $C$ are called internal vertices of $C$. Given a graphoidal cover $\psi$ of $G$, a vertex $v$ is said to be interior to $\psi$ if $v$ is an internal vertex of an element of $\psi$ and is called exterior to $\psi$ otherwise.

Fig. 1 The nine forbidden subgraph characterization of line graphs.

In the next section, we study the distinguishing number and the distinguishing index of line graphs. In Section 3, we consider graphoidal graphs and study their distinguishing number and distinguishing index.

2 Study of $D\left(G\right)$ and $D^{\prime }\left(G\right)$ for the line graphs

For a simple graph $G$, line graph $L\left(G\right)$ is the graph whose vertices are edges of $G$ and two edges $e,e^{\prime }\in V\left(L\left(G\right)\right)=E\left(G\right)$ are adjacent if they share an endpoint in common. The following theorem characterizes the line graphs.

Theorem 2.1

[5] The following statements are equivalent for a graph $G$.

(i)	The graph $G$ is the line graph of some graph.
(ii)	The edges of $G$ can be partitioned into complete subgraphs in such a way that no vertex belongs to more than two of the subgraphs.
(iii)	The graph $K_{1,3}$ is not an induced subgraph of $G$; and if $abc$ and $bcd$ are distinct odd triangles, then $a$ and $d$ are adjacent.
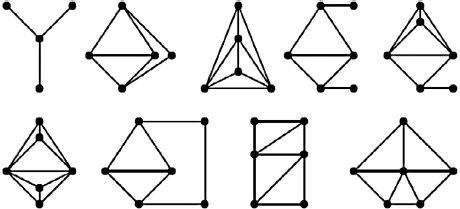
(iv)	None of the nine graphs in Fig. 1 is an induced subgraph of $G$.

To study the distinguishing number and the distinguishing index of $L\left(G\right)$, we need more information about the automorphism group of $L\left(G\right)$. Let ${\gamma }_G:\mathrm{Aut}\left(G\right)\to \mathrm{Aut}\left(L\left(G\right)\right)$ be given by $\left({\gamma }_G\varphi \right)\left(\{u,v\}\right)=\{\varphi \left(u\right),\varphi \left(v\right)\}$ for every $\{u,v\}\in E\left(G\right)$. In [6], Sabidussi proved the following theorem which we need later.

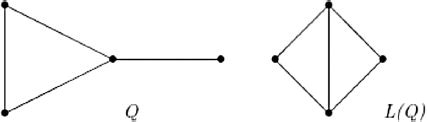
Theorem 2.2

[6] If $G$ is a connected graph that is not $P_2,Q$, or $L\left(Q\right)$, which is $K_4$ with one edge removed, (see Fig. 2 ), then $G$ is a group isomorphism, and so $\mathrm{Aut}\left(G\right)\cong \mathrm{Aut}\left(L\left(G\right)\right)$.

Fig. 2 Graphs $Q$ and $L\left(Q\right)$ of Theorem 2.2.

Now we are ready to obtain the distinguishing number of line graph of a graph. We note that if $G=L\left(Q\right)$, then it is easy to see that $D^{\prime }\left(L\left(Q\right)\right)=2$, while $D\left(L\left(L\left(Q\right)\right)\right)=3$.

Theorem 2.3

If $G$ is a connected graph that is not $P_2$ or $L\left(Q\right)$, then $D\left(L\left(G\right)\right)=D^{\prime }\left(G\right)$.

Proof

If $G=Q$, then it is easy to see that $D^{\prime }\left(Q\right)=D\left(L\left(Q\right)\right)=2$. If $G\ne Q$, first we show that $D\left(L\left(G\right)\right)\le D^{\prime }\left(G\right)$. Let $c:E\left(G\right)\to \{1,\dots ,D^{\prime }\left(G\right)\}$ be an edge distinguishing labeling of $G$. We define $c^{\prime }:V\left(L\left(G\right)\right)\to \{1,\dots ,D^{\prime }\left(G\right)\}$ such that $c^{\prime }\left(e\right)=c\left(e\right)$, where $e\in V\left(L\left(G\right)\right)=E\left(G\right)$. The vertex labeling $c^{\prime }$ is a distinguishing vertex labeling of $L\left(G\right)$, because if $f$ is an automorphism of $L\left(G\right)$ preserving the labeling, then $c^{\prime }\left(f\left(e\right)\right)=c^{\prime }\left(e\right)$, and hence $c\left(f\left(e\right)\right)=c\left(e\right)$ for any $e\in E\left(G\right)$. On the other hand, by Theorem 2.2, $f={\gamma }_G\varphi$ for some automorphism $\varphi$ of $G$. Thus from $c\left(f\left(e\right)\right)=c\left(e\right)$ for any $e\in E\left(G\right)$, we can conclude that $c\left({\gamma }_G\varphi \left(e\right)\right)=c\left(e\right)$ and so $c\left(\{\varphi \left(u\right),\varphi \left(v\right)\}\right)=c\left(\{u,v\}\right)$ for every $\{u,v\}\in E\left(G\right)$. This means that $\varphi$ is an automorphism of $G$ preserving the labeling $c$, and so $\varphi$ is the identity automorphism of $G$. Therefore $f$ is the identity automorphism of $L\left(G\right)$, and hence $D\left(L\left(G\right)\right)\le D^{\prime }\left(G\right)$. For the converse, suppose that $c:V\left(L\left(G\right)\right)\to \{1,\dots ,D\left(L\left(G\right)\right)\}$ is a vertex distinguishing labeling of $L(G$). We define $c^{\prime }:E\left(G\right)\to \{1,\dots ,D\left(L\left(G\right)\right)\}$ such that $c^{\prime }\left(e\right)=c\left(e\right)$ where $e\in E\left(G\right)$. The edge labeling $c^{\prime }$ is a distinguishing edge labeling of $G$. Because if $f$ is an automorphism of $G$ preserving the labeling, then $c^{\prime }\left(f\left(e\right)\right)=c^{\prime }\left(e\right)$, and hence $c\left(f\left(e\right)\right)=c\left(e\right)$ for any $e\in E\left(G\right)$. Then, there exists an automorphism ${\gamma }_{G}f$ of $L\left(G\right)$ such that ${\gamma }_{G}f\left(\{u,v\}\right)=\{f\left(u\right),f\left(v\right)\}$ for every $\{u,v\}\in E\left(G\right)$, by Theorem 2.2. Thus from $c\left(f\left(e\right)\right)=c\left(e\right)$ for any $e\in E\left(G\right)$, we can conclude that $c\left(\{u,v\}\right)=c\left(\{f\left(u\right),f\left(v\right)\}\right)=c\left({\gamma }_{G}f\left(\{u,v\}\right)\right)$ for every $\{u,v\}\in E\left(G\right)$, which means that ${\gamma }_{G}f$ preserves the distinguishing vertex labeling of $L\left(G\right)$, and hence ${\gamma }_{G}f$ is the identity automorphism of $L\left(G\right)$. Therefore $f$ is the identity automorphism of $G$, and so $D^{\prime }\left(G\right)\le D\left(L\left(G\right)\right)$.

An upper bound for the distinguishing index of line graphs follows immediately from the following result of Pilśniak in [7]. A $K_{1,3}$-free graph, called also a claw-free graph, is a graph that does not contain a copy of $K_{1,3}$ as an induced subgraph.

Theorem 2.4

[7] If $G$ is a connected claw-free graph, then $D^{\prime }\left(G\right)\le 3$.

Now by Part (iii) of Theorems 2.1 and 2.4, we have the following theorem.

Theorem 2.5

If $G$ is a connected graph, then $D^{\prime }\left(L\left(G\right)\right)\le 3$.

3 Study of $D\left(G\right)$ and $D^{\prime }\left(G\right)$ for graphoidal graphs

We recall that a graphoidal cover of a graph $G$ is a collection $\psi$ of (not necessarily open) paths in $G$ satisfying the following conditions: every path in $\psi$ has at least two vertices, every vertex of $G$ is an internal vertex of at most one path in $\psi$, and every edge of $G$ is in exactly one path in $\psi$. Let $\psi$ be a graphoidal cover of $G$ and $\Omega (G,\psi )$ denote the intersection graph of $\psi$. Thus the vertices of $\Omega (G,\psi )$ are the paths in $\psi$ and two paths in $\psi$ are adjacent in $\Omega (G,\psi )$ if and only if they have a common vertex. A graph $G$ is said to be graphoidal if there exist a graph $H$ and a graphoidal cover $\psi$ of $H$ such that $G$ is isomorphic to $\Omega (H,\psi )$. First we state and prove the following theorem:

Theorem 3.1

For any positive integer $N$ there exists a graph $G$ with a graphoidal cover $\psi$ for which $|D\left(G\right)-D\left(\Omega (G,\psi )\right)|=N$ and $|D^{\prime }\left(G\right)-D^{\prime }\left(\Omega (G,\psi )\right)|=N$.

Proof

Let $G$ be a graph as shown in Fig. 3. It is easy to see that $D\left(G\right)=D^{\prime }\left(G\right)=2$. A graphoidal cover of $G$ is $\psi =\{P_1,P_2,\dots ,P_{n+1}\}$ where $P_1=(v_1,v_2,\dots ,v_{n+2})$ and $P_i=(v_i,w_i)$ for $2\le i\le n+1$. Thus $\Omega (G,\psi )=K_{1,n}$, and hence $D\left(\Omega (G,\psi )\right)=D^{\prime }\left(\Omega (G,\psi )\right)=n$. Therefore we have the result.

Fig. 3 Graph $G$ in the proof of Theorem 3.1.

To study the distinguishing index of graphoidal graphs, we need some theorems.

Theorem 3.2

[2] If $G$ is a connected graph of order $n\ge 3$, then $D^{\prime }\left(G\right)\le \Delta \left(G\right)$, unless $G$ is $C_3,C_4$ or $C_5$.

Recall that every finite tree $T$ has either a central vertex or a central edge, which is fixed by every automorphism of $T$. A symmetric tree, denoted by $T_{h,d}$, is a tree with a central vertex $v_0$, all leaves at the same distance $h$ from $v_0$ and all the vertices which are not leaves with degree $d$. A bisymmetric tree, denoted by $T_{h,d}^{\prime \prime }$, is a tree with a central edge $e_0$, all leaves at the same distance $h$ from $e_0$ and all the vertices which are not leaves with degree $d$.

Theorem 3.3

[7] Let $G$ be a connected graph that is neither a symmetric nor a bisymmetric tree. If the maximum degree of $G$ is at least 3, then $D^{\prime }\left(G\right)\le \Delta \left(G\right)-1$, unless $G$ is $K_4$ or $K_{3,3}$.

Theorem 3.4

[8] If $T$ is a tree of order $n\ge 3$, then $D\left(T\right)\le \Delta \left(T\right)$. Furthermore, equality is achieved if and only if $T$ is a symmetric tree or a path of odd length.

Before we state the next theorem we need to define some terms: Let $v$ be a vertex of a graph $G$ and let $f$ be a $k$-distinguishing edge labeling of $G$. We say that f is $v$-distinguishing if $f$ is preserved only by the trivial automorphism among the automorphisms $\alpha \in \mathrm{Aut}\left(G\right)$ for which $\alpha \left(v\right)=v$ holds. If $vw$ is an edge of a tree $T$, then let $T_v$ and $T_w$ be the components of $T-\left\{vw\right\}$ with $v\in T_v$ and $w\in T_w$. A family $\mathcal{T}$ consists of those trees $T$ of order at least 3, for which the following conditions are fulfilled: (1) $T$ is a bicentric tree with the central edge $e=vw$, (2) $T_v$ and $T_w$ are isomorphic trees, (3) $T_v$ admits a unique $v$-distinguishing edge $D\left(T\right)$-labeling.

Theorem 3.5

[9] Let $T$ be a tree of order $n\ge 3$. Then $D^{\prime }\left(T\right)=D\left(T\right)+1$ if $T\in \mathcal{T}$, and $D^{\prime }\left(T\right)=D\left(T\right)$ otherwise.

Now, we obtain bounds for the distinguishing index of graphoidal graphs.

Theorem 3.6

Let $G$ be a connected graph and $\psi$ be a graphoidal cover of $G$ such that the order of $\Omega (G,\psi )$ is at least $3$. If $\Omega (G,\psi )\ne C_3,C_5$, then $$1\le D^{\prime }\left(\Omega (G,\psi )\right)\le \left|\psi \right|-1.$$Moreover, $D^{\prime }\left(\Omega (G,\psi )\right)=\left|\psi \right|-1$ if and only if $\Omega (G,\psi )$ is $C_4$, $K_4$ or $K_{1,\left|\psi \right|-1}$.

Proof

By Fig. 5, we can conclude the left inequality. For the right inequality, by contradiction, we suppose that $D^{\prime }\left(\Omega (G,\psi )\right)\ge \left|\psi \right|$. Since $D^{\prime }\left(\Omega (G,\psi )\right)\le \Delta \left(\Omega (G,\psi )\right)$ by Theorem 3.2, we get $\left|\psi \right|\le \Delta \left(\Omega (G,\psi )\right)$, which is a contradiction, since $\Delta \left(\Omega (G,\psi )\right)\le \left|V\left(\Omega (G,\psi )\right)\right|-1=\left|\psi \right|-1$.

If $D^{\prime }\left(\Omega (G,\psi )\right)=\left|\psi \right|-1$, then $D^{\prime }\left(\Omega (G,\psi )\right)=\Delta \left(\Omega (G,\psi )\right)$, by Theorem 3.2, unless for $\Omega (G,\psi )=C_4$. If $\Delta \left(\Omega (G,\psi )\right)\ge 3$, then we have $D^{\prime }\left(\Omega (G,\psi )\right)=\Delta \left(\Omega (G,\psi )\right)$, if and only if $\Omega (G,\psi )$ is a symmetric, a bisymmetric tree, $K_4$ or $K_{3,3}$, by Theorem 3.3. Now since $\Delta \left(\Omega (G,\psi )\right)=\left|\psi \right|-1$, $D^{\prime }\left(\Omega (G,\psi )\right)=\left|\psi \right|-1$ if and only if $\Omega (G,\psi )$ is $C_4$, $K_4$ or $K_{1,\left|\psi \right|-1}$, by Theorems 3.4 and 3.5.

Fig. 4 The graph $G$ and its graphoidal of Theorem 3.7.

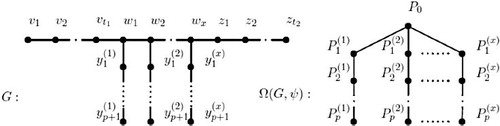
Fig. 5 An example for sharpness of inequality of Theorem 3.9.

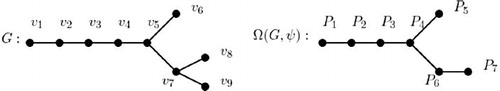
The following theorem states that for every $i$, $2\le i\le \left|\psi \right|-1$, there exists a connected graphoidal graph with the distinguishing index $i$.

Theorem 3.7

Suppose that $x$ and $p$ are positive integers and $(x,p)\ne (1,1)$. If $k=1+xp$ and $d=\lceil \sqrt[p]{x}\rceil$, then there exist a graph $G$ of order $n\ge x(p+2)$ and graphoidal cover $\psi$ of $G$ with $\left|\psi \right|=k$ such that $D^{\prime }\left(\Omega (G,\psi )\right)=d$.

Proof

Let $G$ be a graph in Fig. 4. If $\psi =\{P_0,P_1^{\left(1\right)},\dots ,P_p^{\left(1\right)},\dots ,P_1^{\left(x\right)},\dots ,P_p^{\left(x\right)}\}$ where $P_0=(v_1,\dots ,v_{t_1},w_1,\dots ,w_x,z_1,\dots ,z_{t_2})$ and for every $1\le i\le x$, $P_1^{\left(i\right)}=(w_i,y_1^{\left(i\right)})$, $P_j^{\left(i\right)}=(y_j^{\left(i\right)},y_{j+1}^{\left(i\right)})$ for each $2\le j\le p$, then $\Omega (G,\psi )$ is as shown in Fig. 4. It is easy to compute that $D^{\prime }\left(\Omega (G,\psi )\right)=\lceil \sqrt[p]{x}\rceil$. With respect to integers $t_1$ and $t_2$, we get that $n\ge x(p+2)$.

In the sequel, we give bounds for the distinguishing number of the graphoidal graphs.

Theorem 3.8

Let $G$ be a connected graph of order $n\ge 3$. Then $$D^{\prime }\left(G\right)-2\le D\left(\Omega (G,\psi )\right)\le \left|\psi \right|.$$

Proof

Since $\Omega (G,\psi )$ has $\left|\psi \right|$ vertices, it is clear that $D\left(\Omega (G,\psi )\right)\le \left|\psi \right|$. To prove the left inequality, let $D\left(\Omega (G,\psi )\right)=t$ and $X_i=\{P_{i1},\dots ,P_{i{s}_i}\}$, $1\le i\le t$ be the set of vertices of $\Omega (G,\psi )$ having label $i$ in the distinguishing labeling of $\Omega (G,\psi )$. Now we want to label the edges of $G$ distinguishingly, using $t+2$ labels. For this purpose, for every $i$, $1\le i\le t$, we label the edge set of all paths of $\psi$ (not necessarily open) in $X_i$ of length $j$ with $j$-tuple $(i,t+1,t+2,\dots ,t+2)$ of labels. We note that since there exist the closed paths (cycles) in $\psi$, we need at most three different labels to distinguishing these closed paths. Then we have an edge labeling of $G$ with $t+2$ labels. To show that this edge labeling is distinguishing, we prove that if $f$ is an automorphism of $G$ preserving this edge labeling, then $f$ maps $\psi$ to $\psi$, setwise. In fact, if $P\in \psi$, then $f\left(P\right)$ is a path of the same length as $P$. Since $f$ preserves the edge labeling of $G$, the label of edges of $f\left(P\right)$ is the same as edges of $P$. With respect to the method of labeling of edge set of each path in $\psi$, we conclude that $f\left(P\right)\in \psi$. Hence $f$ maps a path in $\psi$ to a path in $\psi$. Thus $f$ can be considered as an automorphism of $\Omega (G,\psi )$ preserves the distinguishing vertex labeling of $\Omega (G,\psi )$ with $t$ labels. Thus $f$ is the identity automorphism of $\Omega (G,\psi )$, and this means that $f\left(P\right)=P$ for all $P\in \psi$. On the other hand, since we labeled the edge set of each path in $\psi$ distinguishingly with at most three labels, so $f$ fixes all vertices of path $P$, where $P\in \psi$. Thus $f$ is the identity automorphism of $G$.

The bounds of Theorem 3.8 are sharp. For the left inequality, it is sufficient to consider $G=C_i$, $3\le i\le 5$, and $\psi =\left\{C_i\right\}$. Thus $\Omega (G,\psi )=K_1$, and hence $D^{\prime }\left(G\right)=3$ and $D\left(\Omega (G,\psi )\right)=1$. To show that the upper bound of this theorem is sharp, we consider $G=C_3$ and $\psi =\{e_1,e_2,e_3\}$. Thus $\Omega (G,\psi )=C_3$, and hence $\left|\psi \right|=3$ and $D\left(\Omega (G,\psi )\right)=3$.

Theorem 3.9

If $G$ is a connected graph of order $n\ge 3$ and the graphoidal cover $\psi$ of $G$ contains only open paths, then $D^{\prime }\left(G\right)\le D\left(\Omega (G,\psi )\right)+1$.

Proof

The proof is exactly the same as proof of Theorem 3.8, except the method of labeling of edges of paths in $\psi$. Since all paths in $\psi$ are open, then by notation of Theorem 3.8, for every $i$, $1\le i\le t$, we label the edge set of all open paths of $\psi$ in $X_i$ of length $j$ with the $j$-tuple $(i,\underset{(j-1)-times}{\underbrace{t+1,\dots ,t+1}})$ of labels. Then we have an edge labeling of $G$ with $t+1$ labels. To show this edge labeling is distinguishing, we prove that if $f$ is an automorphism of $G$ preserving this edge labeling, then $f$ maps $\psi$ to $\psi$ setwise. In fact, if $P\in \psi$, then $f\left(P\right)$ is a path of the same length as $P$. Since $f$ preserves the edge labeling of $G$, the label of edges of $f\left(P\right)$ is the same as edges of $P$. With respect to the method of labeling of edge set of each path in $\psi$, we conclude that $f\left(P\right)\in \psi$. Hence $f$ maps a path in $\psi$ to a path in $\psi$. Thus $f$ can be considered as an automorphism of $\Omega (G,\psi )$ preserves the distinguishing vertex labeling of $\Omega (G,\psi )$ with $t$ labels. Thus $f$ is the identity automorphism of $\Omega (G,\psi )$, and this means that $f\left(P\right)=P$ for all $P\in \psi$. On the other hand, since we labeled the edge set of each path in $\psi$ distinguishingly with at most two labels, $f$ fixes all vertices of path $P$ where $P\in \psi$. Thus $f$ is the identity automorphism of $G$.

The bound of Theorem 3.9 is sharp. Let $G$ be as shown in Fig. 5. It is easy to obtain that $D^{\prime }\left(G\right)=2$. A graphoidal cover of $G$ is $\psi =\{P_1,P_2,\dots ,P_7\}$ where $P_1=(v_1,v_2)$, $P_2=(v_2,v_3)$, $P_3=(v_3,v_4)$, $P_4=(v_4,v_5)$, $P_5=(v_5,v_6)$, $P_6=(v_5,v_7,v_8)$, and $P_7=(v_8,v_9)$. Thus $\Omega (G,\psi )$ is an asymmetric graph, and hence $D\left(\Omega (G,\psi )\right)=1$.

We conclude the paper with the following theorem, which shows that the value $|D^{\prime }\left(G\right)-D\left(\Omega (G,\psi )\right)|$ can be arbitrary.

Theorem 3.10

For every $i$, $i\ge 0$, there exist a connected graph $G$ and a graphoidal cover $\psi$ of $G$ such that $|D^{\prime }\left(G\right)-D\left(\Omega (G,\psi )\right)|=i$.

Proof

Let $G$ and $\Omega (G,\psi )$ be the two graphs of Theorem 3.7. Since the automorphism group of $G$ has at most one nonidentity automorphism, $D^{\prime }\left(G\right)\le 2$. On the other hand $\Omega (G,\psi )$ is a tree with a central vertex, and so $D\left(\Omega (G,\psi )\right)=D^{\prime }\left(\Omega (G,\psi )\right)=\lceil \sqrt[p]{x}\rceil$, by Theorem 3.5. Now, with respect to the values of $x$ and $p$, we obtain the result.