Perfect 2-colorings of the cubic graphs of order less than or equal to 10

Abstract

Perfect coloring is a generalization of the notion of completely regular codes, given by Delsarte. A perfect $m$-coloring of a graph $G$ with $m$ colors is a partition of the vertex set of $G$ into m parts $A_1$, . . . , $A_m$ such that, for all $i,j\in \{1,\dots ,m\}$, every vertex of $A_i$ is adjacent to the same number of vertices, namely, $a_{ij}$ vertices, of $A_j$ . The matrix $A={\left(a_{ij}\right)}_{i,j\in \{1,\dots ,m\}}$, is called the parameter matrix. We study the perfect 2-colorings (also known as the equitable partitions into two parts) of the cubic graphs of order less than or equal to 10. In particular, we classify all the realizable parameter matrices of perfect 2-colorings for the cubic graphs of order less than or equal to 10.

Keywords:

• Perfect coloring
• Equitable partition
• Cubic graph
• Parameter matrix

1 Introduction

The concept of a perfect $m$-coloring plays an important role in graph theory, algebraic combinatorics, and coding theory (completely regular codes). There is another term for this concept in the literature as “equitable partition” (see [1]).

The existence of completely regular codes in graphs is a historical problem in mathematics. Completely regular codes are a generalization of perfect codes. In 1973, Delsarte conjectured the non-existence of perfect codes in Johnson graphs. Therefore, some effort has been done on enumerating the parameter matrices of some Johnson graphs, including $J(6,3)$, $J(7,3)$, $J(8,3)$, $J(8,4)$, and $J(v,3)$ ($v$ odd) (see [2–4]).

Fon-Der-Flass enumerated the parameter matrices of $n$-dimensional cube for $n<24$. He also obtained some constructions and a necessary condition for the existence of perfect 2-colorings of the $n$-dimensional cube with a given parameter matrix (see [5–7]). In [8–11] perfect 2-colorings and perfect 3-colorings of some graphs were described. So for cubic graphs of order less than or equal to 10, the problem of existence of perfect 2-colorings was open. In this article, we enumerate the parameter matrices of all perfect 2-colorings of the cubic graphs of order less than or equal to $10$.

2 Preliminaries

Definition 2.1

For each graph $G$ and each integer $m$, a mapping $T:V\left(G\right)\to \{1,\dots ,m\}$ is called a perfect $m$-coloring with matrix $A={\left(a_{ij}\right)}_{i,j\in \{1,\dots ,m\}}$, if it is surjective, and for all $i,j$, for every vertex of color $i$, the number of its neighbors of color $j$ is equal to $a_{ij}$. The matrix $A$ is called the parameter matrix of a perfect coloring. When $m=2$, we denote the two colors by W and B representing white and black respectively.

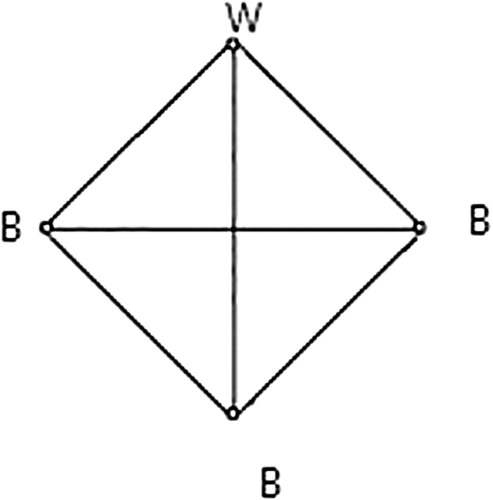
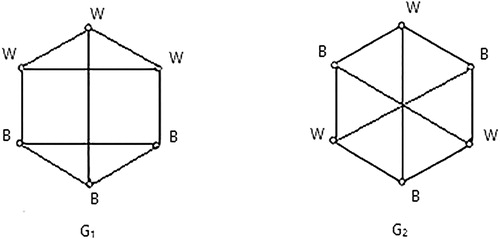
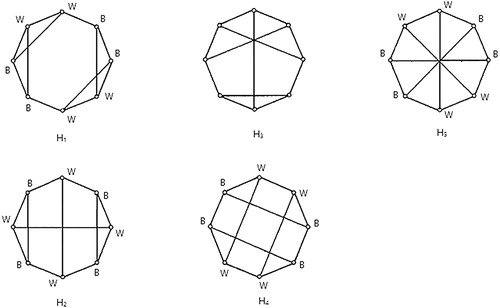
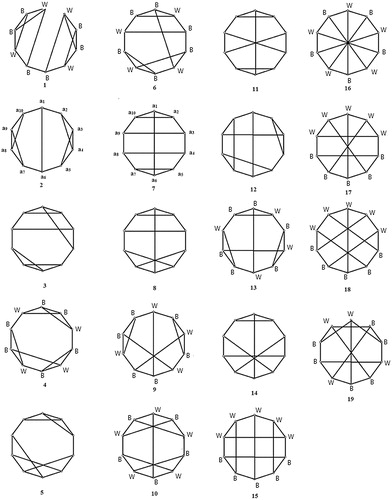
A cubic graph is a 3-regular graph. Cubic graphs of order less than or equal to 10 are given in Figs. 1–4. Wherever possible the vertices of the graph are labeled with B or W giving a perfect 2-coloring.

Fig. 1 Connected cubic graph of order $4$.

Fig. 2 Connected cubic graphs of order $6$.

Fig. 3 Connected cubic graphs of order $8$.

Fig. 4 Connected cubic graphs of order $10$.

Now, we first give some results concerning necessary conditions for the existence of perfect 2-colorings of a $k$-regular graph with a given parameter matrix $A={\left(a_{ij}\right)}_{i,j=1,2}$.

The simplest condition for the existence of a perfect 2-colorings of a $k$-regular graph with the matrix $\left[\begin{array}{cc}\hfill a_{11}\hfill & \hfill a_{12}\hfill \\ \hfill a_{21}\hfill & \hfill a_{22}\hfill \end{array}\right]$ is: $$a_{11}+a_{12}=a_{21}+a_{22}=k.$$If $G$ is connected, then $a_{12}$ and $a_{21}$ are both non-zero. By the given conditions, we can see that a parameter matrix of a perfect 2-coloring of cubic graphs must be one of the following matrices: $A_1=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 3\hfill \\ \hfill 3\hfill & \hfill 0\hfill \end{array}\right],A_2=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 3\hfill \\ \hfill 2\hfill & \hfill 1\hfill \end{array}\right],A_3=\left[\begin{array}{cc}\hfill 2\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right],A_4=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 2\hfill \\ \hfill 2\hfill & \hfill 1\hfill \end{array}\right],A_5=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 3\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right],A_6=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 2\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right].$

The next proposition gives a formula for calculating the number of white vertices in a perfect 2-coloring.

Proposition 2.2

[2] If $W$ is the set of white vertices in a perfect 2-coloring of a graph $G$ with matrix $A={\left(a_{ij}\right)}_{i,j=1,2}$, then $$\left|W\right|=\left|V\left(G\right)\right|\frac{a_{21}}{a_{12}+a_{21}}.$$

The number $\lambda$ is called an eigenvalue of a graph $G$, if $\lambda$ is an eigenvalue of the adjacency matrix of this graph. The number $\theta$ is called an eigenvalue of a perfect coloring $T$ into m colors with the matrix $A$, if $\theta$ is an eigenvalue of $A$. The next theorem demonstrates the connection between the introduced notions.

Theorem 2.3

[12] If $T$ is a perfect coloring of a graph $G$ in $m$ colors, then any eigenvalue of $T$ is an eigenvalue of $G$.

Corollary 2.4

Every perfect 2-coloring of a $k$-regular graph with parameter matrix $\left[\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill c\hfill & \hfill d\hfill \end{array}\right]$ has two eigenvalues: one is $k$, and the other is $a-c$ such that we obviously have $a-c\ne k$. So, from Theorem 2.3 , we conclude that $a-c$ is an eigenvalue of a $k$-regular connected graph which is not equal to $k$.

3 Main results

In this section, we enumerate the parameter matrices of all perfect 2-colorings of the cubic connected graphs of order less than or equal to 10. Any cubic graph of order $4$ is isomorphic to $K_4$ and for the perfect 2-coloring of this graph given in Fig. 1, the parameter matrix is $A_5$. Also, it follows from Proposition 2.2 that the matrices $A_2$ and $A_6$ cannot be parameter matrices. In the next theorems, we introduce the parameter matrices for cubic graphs of order $6$, $8$, and $10$.

Theorem 3.1

The graph $G_1$ has no perfect 2-coloring with parameter matrix $A_4$.

Proof

Suppose there exists a perfect 2-coloring $T$ of $G_1$ with matrix $A_4$. Then each vertex with color 1 has one adjacent vertex with color 2. We now have two possibilities:

(1) $T\left(a_2\right)=T\left(a_6\right)=1$ and $T\left(a_4\right)=2$.

(2) $T\left(a_4\right)=T\left(a_5\right)=1$ and $T\left(a_2\right)=2$.

In both cases we get $T\left(a_3\right)=T\left(a_5\right)=2$, which is a contradiction with the second row of $A_4$. Hence $G_1$ has no perfect 2-coloring with matrix $A_4$.

Theorem 3.2

The graph $G_2$ has no perfect 2-coloring with parameter matrix $A_6$.

Proof

The proof is similar to the proof of Theorem 3.1.

Theorem 3.3

The graph $G_1$ has perfect 2-coloring with parameter matrices $\{A_3,A_6\}$ and graph $G_2$ has perfect 2-coloring with parameter $A_1$.

Proof

For the perfect coloring of $G_1$ and $G_2$ given in Fig. 2, the corresponding parameter matrices are $A_3$ and $A_1$ respectively. Also the mapping defined by $T\left(a_1\right)=T\left(a_2\right)=T\left(a_6\right)=1$ and $T\left(a_3\right)=T\left(a_4\right)=T\left(a_5\right)=2,$ gives a perfect 2-coloring of $G_1$ with matrix $A_3$.

Theorem 3.4

The graph $H_1$ has no perfect 2-coloring with parameter matrix $A_3$.

Proof

Suppose there exists a perfect 2-coloring $T$ of $H_1$ with matrix $A_3$. Then each vertex with color 1 has two adjacent vertices with color 1. We now have three possibilities:

(1) $T\left(a_2\right)=T\left(a_3\right)=1$ and $T\left(a_8\right)=2$.

(2) $T\left(a_8\right)=T\left(a_2\right)=1$ and $T\left(a_3\right)=2$.

(3) $T\left(a_8\right)=T\left(a_3\right)=1$ and $T\left(a_2\right)=2$.

In case 1 we get $T\left(a_4\right)=2$, which is a contradiction with the second row of matrix $A_3$. In other both cases we get a contradiction with the second row of $A_4$. Hence $H_1$ has no perfect 2-coloring with matrix $A_3$.

Theorem 3.5

The graph $H_2$ has no perfect 2-coloring with parameter matrices $A_3$ and $A_6$.

Proof

The proof is similar to the proof of Theorem 3.4.

Theorem 3.6

The graph $H_5$ has no perfect 2-coloring with parameter matrix $A_5$.

Proof

The proof is similar to the proof of Theorem 3.4.

Theorem 3.7

The Graphs $H_1$, $H_2$, $H_4$ and $H_5$ of order $8$ have perfect 2-colorings.

Proof

For the perfect coloring of $\left\{H_1,H_2\right\}$ and $\left\{H_4,H_5\right\}$ given in Fig. 3, the corresponding parameter matrices are $A_4$ and $A_3$ respectively. Also the mapping defined by: $$T\left(a_2\right)=T\left(a_7\right)=1,T\left(a_1\right)=T\left(a_3\right)=T\left(a_4\right)=T\left(a_5\right)=T\left(a_6\right)=T\left(a_8\right)=2,$$gives a perfect 2-coloring of $H_1$ with matrix $A_5$, the mappings defined by: $$T_1\left(a_1\right)=T_1\left(a_3\right)=T_1\left(a_5\right)=T_1\left(a_7\right)=1,T_1\left(a_2\right)=T_1\left(a_4\right)=T_1\left(a_6\right)=T_1\left(a_8\right)=2,T_2\left(a_1\right)=T_2\left(a_3\right)=T_2\left(a_6\right)=T_2\left(a_8\right)=1,T_2\left(a_2\right)=T_2\left(a_4\right)=T_2\left(a_5\right)=T_2\left(a_7\right)=2,T_3\left(a_1\right)=T_3\left(a_6\right)=1,T_3\left(a_2\right)=T_3\left(a_3\right)=T_3\left(a_4\right)=T_3\left(a_5\right)=T_3\left(a_7\right)=T_3\left(a_8\right)=2,$$gives a perfect 2-colorings of $H_4$ with matrices $A_1$, $A_4$ and $A_5$, respectively and the mappings defined by: $$T\left(a_1\right)=T\left(a_3\right)=T\left(a_5\right)=T\left(a_7\right)=1,T\left(a_2\right)=T\left(a_4\right)=T\left(a_6\right)=T\left(a_8\right)=2,$$gives a perfect 2-coloring of $H_5$ with matrix $A_4$.

Theorem 3.8

The parameter matrices of cubic graphs of order $10$ are listed in Table 1.

Table 1 The parameter matrices of cubic graphs of order 10.

Graphs	Matrix $A_1$	Matrix $A_2$	Matrix $A_3$
1	$\times$	$\surd$	$\times$
2	$\times$	$\times$	$\times$
3	$\times$	$\times$	$\times$
4	$\times$	$\surd$	$\times$
5	$\times$	$\surd$	$\times$
6	$\times$	$\surd$	$\times$
7	$\times$	$\times$	$\times$
8	$\times$	$\times$	$\times$
9	$\times$	$\surd$	$\times$
10	$\surd$	$\surd$	$\times$
11	$\times$	$\times$	$\times$
12	$\times$	$\times$	$\times$
13	$\times$	$\surd$	$\times$
14	$\times$	$\times$	$\times$
15	$\times$	$\times$	$\times$
16	$\surd$	$\times$	$\times$
17	$\times$	$\times$	$\times$
18	$\times$	$\times$	$\times$
19	$\times$	$\surd$	$\surd$

Proof

As it has been shown in the previous section, only matrices $A_1$ , $A_2$, …, $A_6$ can be parameter matrices. With consideration the eigenvalues of cubic graphs, and using Proposition 2.2 and Theorem 2.3, it can be seen that the connected cubic graphs with 10 vertices can have perfect $2$-coloring with matrices $A_1$, $A_2$, $A_3$ and $A_4$ which is represented by Table 2. For the perfect coloring of graphs $\left\{1,2,4,6,7,9,13,15,17,18,19\right\}$ and graphs $\left\{10,16\right\}$ given in Fig. 4, the corresponding parameter matrices are $A_2$ and $A_1$ respectively. Also the mapping defined by: $$T\left(a_1\right)=T\left(a_3\right)=T\left(a_4\right)=T\left(a_6\right)=T\left(a_8\right)=T\left(a_9\right)=1,T\left(a_2\right)=T\left(a_5\right)=T\left(a_7\right)=T\left(a_{10}\right)=2.$$gives a perfect 2-coloring of graph $10$ with matrix $A_2$ and the mapping defined by: $$T\left(a_2\right)=T\left(a_3\right)=T\left(a_4\right)=T\left(a_7\right)=T\left(a_8\right)=1,T\left(a_1\right)=T\left(a_5\right)=T\left(a_6\right)=T\left(a_9\right)=T\left(a_{10}\right)=2.$$gives a perfect 2-coloring of graph $19$ with matrix $A_3$.

There are no perfect 2-colorings with the matrices $A_3$ for graph $1$. Suppose there exists a perfect 2-coloring $T$ of $1$ with matrix $A_3$. Then each vertex with color 1 has two adjacent vertices with color 1. We now have three possibilities:

(1) $T\left(a_3\right)=T\left(a_5\right)=1$ and $T\left(a_2\right)=2$.

(2) $T\left(a_2\right)=T\left(a_5\right)=1$ and $T\left(a_3\right)=2$.

(3) $T\left(a_2\right)=T\left(a_3\right)=1$ and $T\left(a_5\right)=2$.

In all three cases, the vertex by color 2 has two adjacent vertex with color 1, which is a contradiction with the second row of $A_3$. Hence graph $1$ has no perfect 2-coloring with matrix $A_3$.

About other graphs in Fig. 4, similarly, we can get the same result as in Table 1.

Table 2 The possibility of existence a perfect 2-coloring to cubic graphs of order 10.

Graphs	Matrix $A_1$	Matrix $A_2$	Matrix $A_3$	Matrix $A_4$
1	$\times$	$\surd$	$\surd$	$\surd$
2	$\times$	$\surd$	$\surd$	$\surd$
3	$\times$	$\times$	$\surd$	$\times$
4	$\times$	$\surd$	$\surd$	$\times$
6	$\times$	$\surd$	$\surd$	$\surd$
7	$\times$	$\times$	$\times$	$\surd$
9	$\times$	$\surd$	$\surd$	$\surd$
10	$\surd$	$\surd$	$\surd$	$\surd$
13	$\times$	$\surd$	$\times$	$\surd$
14	$\times$	$\times$	$\times$	$\surd$
15	$\times$	$\times$	$\times$	$\surd$
16	$\surd$	$\times$	$\times$	$\times$
17	$\times$	$\times$	$\times$	$\surd$
18	$\times$	$\surd$	$\surd$	$\surd$
19	$\times$	$\surd$	$\times$	$\surd$