On constant sum partitions and applications to distance magic-type graphs

Abstract

Let $G$ be an additive abelian group of order $n$ and let $n=a_1+a_2+...+a_p$ be a partition of $n$ where $1\le a_1\le a_2\le \cdots \le a_p.$ A constant sum partition (or $t$-sum partition) of $G$ is a pairwise disjoint union of subsets $A_1,A_2,\dots ,A_p$ such that $G=A_1\cup A_2\cup \cdots \cup A_p,$ $\left|A_i\right|=a_i,$ and ${\sum }_{a\in A_i}^{}a=t,$ for some fixed $t\in G$ and every $1\le i\le p.$ In 2009, Kaplan, Lev, and Roditty proved that a 0-sum partition of the cyclic group ${\mathbb{Z}}_n$ exists for $n$ odd if and only if $a_2\ge 2.$ In this paper, we address the case when $n$ is even. In particular, we show that a $\frac{n}{2}$-sum partition of ${\mathbb{Z}}_n$ exists for $n$ even and $p$ odd if and only if $a_2\ge 2.$ Moreover, we provide applications to distance magic-type graphs including the classification of ${\mathbb{Z}}_n$-distance magic complete $p$-partite graphs for $p$ odd.

Keywords:

• Constant sum partition
• Group distance magic graphs
• Orientable distance magic graphs

1 Constant sum partitions

Let $n=a_1+a_2+\cdots +a_p$ be a partition of the positive integer $n$, where $1\le a_1\le a_2\le \cdots \le a_p$. Let $G$ be an additive abelian group of order $n$ and $g\in G$. A constant sum partition (or $g$-sum partition) of $G$ is a pairwise disjoint union of subsets $A_1,A_2,\dots ,A_p$ such that $G=A_1\cup A_2\cup \cdots \cup A_p$, $\left|A_i\right|=a_i$, and ${\sum }_{a\in A_i}^{}a=g$, for every $1\le i\le p$. If such a partition of $G$ can be found for every partition of $n$ with $a_2\ge 2$, we say that $G$ has the constant sum property, $CSP\left(p\right)$. If $G$ has the $CSP\left(p\right)$ property and $g=0$, then we say $G$ has the $ZSP\left(p\right)$ property. Kaplan et al. proved the following in [1].

Theorem 1

[1] The cyclic group ${\mathbb{Z}}_n$ has the $ZSP\left(n\right)$ property if and only if $n$ is odd.

In this paper, we focus on constant sum partitions of the cyclic group of even order. We begin with a necessary condition.

Observation 2

Let $n=a_1+a_2+\cdots +a_p$ be a partition of the integer $n$. If $n$ is even and a $g$-sum partition of ${\mathbb{Z}}_n$ exists, then $pg\equiv \frac{n}{2}(modn)$.

Proof

Since a $g$-sum partition of ${\mathbb{Z}}_n$ exists, $pg={\sum }_{a\in G^{}}a=\frac{n}{2}\equiv \frac{n}{2}(modn)$.□

Because the constant sum partition of any group is trivial when $p=1$, we will assume $p\ge 2$ from now on. From Observation 2, we obtain the following corollaries. Proofs of the corollaries are left to the reader.

Corollary 3

Let $n=a_1+a_2+\cdots +a_p$ be a partition of the integer $n$. If $n\equiv 2(mod4)$ and there exists a $g$-sum partition of ${\mathbb{Z}}_n$, then both $g$ and $p$ are odd.

Corollary 4

Let $n=a_1+a_2+\cdots +a_p$ be a partition of the integer $n$. If$n\equiv 4(mod8)$ and there exists a $g$-partition of ${\mathbb{Z}}_n$, then$p⁄\equiv 0(mod4)$.

Our next result identifies necessary and sufficient conditions for the existence of a constant sum partition of the cyclic group for an even integer with an odd number of parts. Let $S$ be a set of integers. For any subset $A$ of $S$, we say $A$ is a $t$-sum subset of $A$ if the sum of all the elements in $A$ is $t$. We denote by $-S$ the set $\{-a|a\in S\}$.

Theorem 5

If $n$ is even and $p$ is odd, then ${\mathbb{Z}}_n$ has the $CSP\left(p\right)$ property.

Proof

Let $n=a_1+a_2+\cdots +a_p$ with $1\le a_1\le a_2\le \cdots \le a_p$, and $A=\{1,2,\dots ,n\}$. We will prove the theorem by partitioning $A$ into pairwise disjoint subsets $A_1,A_2,\dots ,A_p$ such that $\left|A_i\right|=a_i$ and ${\sum }_{a\in A_i}^{}a\equiv \frac{n}{2}(modn)$, for every $1\le i\le p$. The necessity of $a_2\ge 2$ is obvious. Relabel indices so that $n=a_1+a_2+\cdots +a_d+a_{d+1}+\cdots +a_{d+t}$ with $2\le a_1\le \cdots \le a_d$, $1\le a_{d+1}\le \cdots \le a_{d+t}$, where $a_i$ is even for $i=1,2,\dots ,d$ and odd for $i=d+1,d+2,\dots ,d+t$. The assumption of $n$ even and $p$ odd implies $t$ is even and $d$ is odd.

Observe that since every element in $A-\{n,\frac{n}{2}\}$ can be written as $\frac{n}{2}+a$ for a unique $a\in S=\{\pm 1,\pm 2,\dots ,\pm (\frac{n}{2}-1)\}$, it suffices to partition the set $S$ into $(t-2)$ 0-sum subsets of size 3, $(d+1)$ $\frac{n}{2}$-sum subsets of size 2, and $\left(\frac{n-3t-2d+2}{2}\right)$ 0-sum subsets of size 2, all pairwise disjoint.

First we construct the $\frac{n}{2}$-sum subsets of size 2. Let $$\begin{array}{ccc}{C}_1\hfill & =\hfill & \{\frac{t}{2},\frac{n-t}{2}\},\hfill \\ C_2\hfill & =\hfill & \{\frac{t}{2}+1,\frac{n-t-2}{2}\},\hfill \\ \hfill & ⋮\hfill & \hfill \\ C_{\frac{d+1}{2}}\hfill & =\hfill & \{\frac{t+d-1}{2},\frac{n-t-d+1}{2}\},\hfill \end{array}$$and $C_{\frac{d+2i+1}{2}}=-C_i$ for $i=1,2,\dots ,\frac{d+1}{2}$.

If $t\ge 4$ and $t\equiv 0(mod4)$, construct the $0$-sum subsets of size 3 as follows. Let $$\begin{array}{ccc}{B}_1\hfill & =\hfill & \{1,\frac{3t+2d-2}{4},-\left(\frac{3t+2d+2}{4}\right)\},\hfill \\ B_2\hfill & =\hfill & \{2,\frac{2n-t-4}{4},-\left(\frac{2n-t+4}{4}\right)\},\hfill \\ B_3\hfill & =\hfill & \{3,\frac{3t+2d-6}{4},-\left(\frac{3t+2d+6}{4}\right)\},\hfill \\ B_4\hfill & =\hfill & \{4,\frac{2n-t-8}{4},-\left(\frac{2n-t+8}{4}\right)\},\hfill \\ \hfill & ⋮\hfill & \hfill \\ B_{\frac{t}{2}-4}\hfill & =\hfill & \{\frac{t}{2}-4,\frac{n-t+4}{2},-(\frac{n}{2}-2)\},\hfill \\ B_{\frac{t}{2}-3}\hfill & =\hfill & \{\frac{t}{2}-3,\frac{t+d+3}{2},-\left(\frac{2t+d-3}{2}\right)\},\hfill \\ B_{\frac{t}{2}-2}\hfill & =\hfill & \{\frac{t}{2}-2,\frac{n-t+2}{2},-(\frac{n}{2}-1)\}.\hfill \\ B_{\frac{t}{2}-1}\hfill & =\hfill & \{\frac{t}{2}-1,\frac{t+d+1}{2},-\left(\frac{2t+d-1}{2}\right)\}.\hfill \end{array}$$

Whereas if $t\ge 2$ and $t\equiv 2(mod4)$, let $$\begin{array}{ccc}{B}_1\hfill & =\hfill & \{1,\frac{2n-t-2}{4},-\left(\frac{2n-t+2}{4}\right)\},\hfill \\ B_2\hfill & =\hfill & \{2,\frac{3t+2d-4}{4},-\left(\frac{3t+2d+4}{4}\right)\},\hfill \\ B_3\hfill & =\hfill & \{3,\frac{2n-t-6}{4},-\left(\frac{2n-t+6}{4}\right)\},\hfill \\ B_4\hfill & =\hfill & \{4,\frac{3t+2d-8}{4},-\left(\frac{3t+2d+8}{4}\right)\},\hfill \\ \hfill & ⋮\hfill & \hfill \\ B_{\frac{t}{2}-4}\hfill & =\hfill & \{\frac{t}{2}-4,\frac{n-t+4}{2},-(\frac{n}{2}-2)\},\hfill \\ B_{\frac{t}{2}-3}\hfill & =\hfill & \{\frac{t}{2}-3,\frac{t+d+3}{2},-\left(\frac{2t+d-3}{2}\right)\},\hfill \\ B_{\frac{t}{2}-2}\hfill & =\hfill & \{\frac{t}{2}-2,\frac{n-t+2}{2},-(\frac{n}{2}-1)\}.\hfill \\ B_{\frac{t}{2}-1}\hfill & =\hfill & \{\frac{t}{2}-1,\frac{t+d+1}{2},-\left(\frac{2t+d-1}{2}\right)\}.\hfill \end{array}$$

In either case, let $B_{\frac{t}{2}+i-1}=-B_i$ for $i=1,2,\dots ,\frac{t}{2}-1$. These sets are pairwise disjoint as long as $\frac{n-t-d+1}{2}>\frac{t+d-1}{2}$ (from the $C_i^{\prime }s$), $\frac{t+d+1}{2}>\frac{t}{2}-1$ and $\frac{n-t+2}{2}>\frac{2t+d-1}{2}$ (from the $B_i$’s). All three inequalities are satisfied by assumption since $n\ge 3t+2d$. Also, notice the integer $c\in C_i$ if and only if $-c\in C_{\frac{d+2i+1}{2}}$, and the integer $b\in B_i$ if and only if $-b\in B_{\frac{t}{2}+i-1}$. Therefore, the $n-3t-2d+2$ remaining elements in $S-{\bigcup }_i{B}_i-{\bigcup }_j{C}_j$ may be partitioned into $\frac{n-3t-2d+2}{2}$ pairwise disjoint 0-sum pairs, completing the desired partition of $S$. Place these 0-sum pairs arbitrarily into $d+t$ sets (keeping the 0-sum pairs together) $D_i$ so that $\left|D_i\right|=a_i-2$ for $i=1,2,\dots ,d$ and if $a_{d+1}=1$, then $D_{d+1}=0̸$ and $\left|D_i\right|=a_i-3$ for $i=d+2,d+3,\dots ,d+t$. Whereas if $a_{d+1}\ge 3$, then $\left|D_i\right|=a_i-3$ for $i=d+1,d+2,\dots ,d+t-1$ and $\left|D_{d+t}\right|=a_{d+t}-1$.

If $a_{d+1}=1$, let $$\begin{array}{ccc}{A}_i\hfill & =\hfill & \{\frac{n}{2}+a:a\in C_i\cup D_i\}\text{for}i=1,2,\dots ,d,\hfill \\ A_{d+1}\hfill & =\hfill & \left\{\frac{n}{2}\right\},\hfill \\ A_{d+2}\hfill & =\hfill & \{n,\frac{n}{2}+a:a\in C_{d+1}\cup D_{d+2}\},\text{and}\hfill \\ A_i\hfill & =\hfill & \{\frac{n}{2}+a:a\in B_{i-d-2}\cup D_i\}\text{for}i=d+3,d+4,\dots ,d+t.\hfill \end{array}$$If $a_{d+1}\ge 3$, let $$\begin{array}{ccc}{A}_i\hfill & =\hfill & \{\frac{n}{2}+a:a\in C_i\cup D_i\}\text{for}i=1,2,\dots ,d,\hfill \\ A_{d+i}\hfill & =\hfill & \{\frac{n}{2}+a:a\in B_i\cup D_{d+i}\}\text{for}i=1,2,\dots ,t-2.\hfill \\ A_{d+t-1}\hfill & =\hfill & \{n,\frac{n}{2}+a:a\in C_{d+1}\cup D_{d+t-1}\},\text{and}\hfill \\ A_{d+t}\hfill & =\hfill & \{\frac{n}{2},\frac{n}{2}+a:a\in D_{d+t}\},\hfill \end{array}$$

In both cases, we have partitioned $A$ into pairwise disjoint subsets $A_1,A_2,\dots ,A_{d+t}$ such that $\left|A_i\right|=a_i$ and ${\sum }_{a\in A_i}^{}a\equiv \frac{n}{2}(modn)$, for every $1\le i\le d+t$, proving the theorem.□

Example 6

Find a constant sum partition of ${\mathbb{Z}}_{42}$ for the partition $42=2+2+4+4+6+3+3+3+3+5+7$.

We have $n=42$, $d=5$, and $t=6$. The partition of $S=\{\pm 1,\pm 2,\dots ,\pm 20\}$ is $$\begin{array}{cccccc}{C}_1\hfill & =\hfill & \{3,18\},\hfill & D_1\hfill & =\hfill & 0̸,\hfill \\ C_2\hfill & =\hfill & \{4,17\},\hfill & D_2\hfill & =\hfill & 0̸,\hfill \\ C_3\hfill & =\hfill & \{5,16\},\hfill & D_3\hfill & =\hfill & \{7,-7\},\hfill \\ C_4\hfill & =\hfill & \{-3,-18\},\hfill & D_4\hfill & =\hfill & \{9,-9\},\hfill \\ C_5\hfill & =\hfill & \{-4,-17\},\hfill & D_5\hfill & =\hfill & \{10,-10,11,-11\},\hfill \\ C_6\hfill & =\hfill & \{-5,-16\},\hfill & D_6\hfill & =\hfill & 0̸,\hfill \\ B_1\hfill & =\hfill & \{1,19,-20\},\hfill & D_7\hfill & =\hfill & 0̸,\hfill \\ B_2\hfill & =\hfill & \{2,6,-8\},\hfill & D_8\hfill & =\hfill & 0̸,\hfill \\ B_3\hfill & =\hfill & \{-1,-19,20\},\hfill & D_9\hfill & =\hfill & 0̸,\hfill \\ B_4\hfill & =\hfill & \{-2,-6,8\},\hfill & D_{10}\hfill & =\hfill & \{12,-12\},\hfill \\ \hfill & \hfill & \hfill & D_{11}\hfill & =\hfill & \{13,-13,14,-14,15,-15\}.\hfill \end{array}$$The corresponding constant sum partition of $A=\{1,2,\dots ,42\}$ is $$\begin{array}{cccccc}{A}_1\hfill & =\hfill & \{24,39\},\hfill & A_7\hfill & =\hfill & \{23,27,13\},\hfill \\ A_2\hfill & =\hfill & \{25,38\},\hfill & A_8\hfill & =\hfill & \{20,2,41\},\hfill \\ A_3\hfill & =\hfill & \{26,37,28,14\},\hfill & A_9\hfill & =\hfill & \{19,15,29\},\hfill \\ A_4\hfill & =\hfill & \{18,3,30,12\},\hfill & A_{10}\hfill & =\hfill & \{42,16,5,33,9\},\hfill \\ A_5\hfill & =\hfill & \{17,4,31,11,32,10\},\hfill & A_{11}\hfill & =\hfill & \{21,34,8,35,7,36,6\}.\hfill \\ A_6\hfill & =\hfill & \{22,40,1\},\hfill \end{array}$$Replacing the integer $42$ in $A_{10}$ with $0$, we obtain a 21-sum partition of ${\mathbb{Z}}_{42}$. □

One may wonder what can be said of the existence of constant sum partitions of the cyclic group for even integers having an even number of parts. If all partite sets are the same size, the following can be said.

Theorem 7

Let $n=c+c+\cdots +c=cp$ be a partition of the positive integer $n$. If $c$ is even, then${\mathbb{Z}}_n$ can be partitioned into pairwise disjoint subsets $A_1,A_2,\dots ,A_p$ such that $\left|A_i\right|=c$ and ${\sum }_{a\in A_i}^{}a=\frac{c}{2}$, for every $1\le i\le p$.

Proof

Define disjoint $1$-sum pairs $P_i=\{i,-i+1\}$ for $i=1,2,\dots ,\frac{n}{2}$. Let $A_i=P_1\cup P_2\cup \cdots \cup P_{\frac{c}{2}}$ for $i=1,2,\dots ,p$. Since $\left|A_i\right|=c$ and ${\sum }_{a\in A_i}^{}a=\frac{c}{2}$ for every $1\le i\le p$, we have proved the theorem.□

2 Distance magic-type graphs

Let $G=(V,E)$ be a simple graph with $\left|V\right|=n$. Let $f:V\to \{1,2,\dots ,n\}$ be a bijection and for all $x\in V$, define the weight of the vertex as $w\left(x\right)={\sum }_{y:xy\in E}^{}f\left(y\right)$. If $w\left(x\right)=\mu$ for some number $\mu$ and all $x$, we say $f$ is a distance magic labeling of $G$ (with magic constant $\mu$) and call $G$ a distance magic graph.

If instead of using integers as labels group elements are used, then the following generalization of distance magic labeling is possible. Let $\Gamma$ be an additive abelian group of order $n$ and let $g:V\to \Gamma$ be a bijection. If there exists $\gamma \in \Gamma$ such that $w\left(x\right)=\gamma$ for all $x\in V$, we say $g$ is a $\Gamma$-distance magic labeling of $G$ and call $G$ a $\Gamma$-distance magic graph.

A further generalization to directed graphs is possible as follows. Let $\vec{G}=(V,A)$ be a directed graph and let $l:V\to \Gamma$ be a bijection. Define the weight of a vertex, $w\left(x\right)={\sum }_{y:\overrightarrow{xy}\in A}^{}l\left(y\right)-{\sum }_{y:\overrightarrow{yx}\in A}^{}l\left(y\right)$, for all $x\in V$. If $w\left(x\right)=g$ for some $g\in \Gamma$ and all $x$, we say $l$ is a directed$\Gamma$-distance magic labeling of $\vec{G}$ and call the underlying simple graph $G$ an orientable $\Gamma$-distance magic graph.

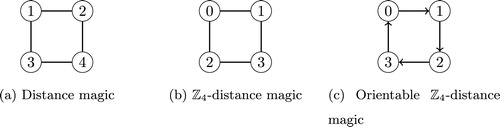
Fig. 1 shows side-by-side labelings of each of the three magic-type labelings of the 4-cycle, $C_4$.

Fig. 1 Magic-type labelings of $C_4$.

3 Complete $p$-partite graphs

It is an easy observation that the complete $p$-partite graph is not ${\mathbb{Z}}_n$-distance magic when $p=1$. The next theorem completely classifies ${\mathbb{Z}}_n$-distance magic labelings of complete bipartite graphs [2], complete tripartite graphs [3], and complete $p$-partite graphs for $n$ odd [2].

Theorem 8

[2,3] Let $G=K_{n_1,n_2,\dots ,n_p}$ be a complete $p$-partite graph with $1\le n_1\le n_2\le \cdots \le n_p$, and $n=n_1+n_2+\cdots +n_p$. If$p=2$, the graph$G$ is${\mathbb{Z}}_n$-distance magic if and only if $n⁄\equiv 2(mod4)$. If $p=3$,$G$ is${\mathbb{Z}}_n$-distance magic if and only if $n_2\ge 2$. If $n$ is odd, $G$ is${\mathbb{Z}}_n$-distance magic if and only if $n_2\ge 2$.

The following three theorems apply our results from Section 1.

Theorem 9

Let $G=K_{n_1,n_2,\dots ,n_p}$ be a complete $p$-partite graph such that $p$ is odd, $1\le n_1\le n_2\le \cdots \le n_p$, and$n=n_1+n_2+\cdots +n_p$ is even. The graph $G$ is${\mathbb{Z}}_n$-distance magic if and only if $n_2\ge 2$.

Proof

Let $G=K_{n_1,n_2,\dots ,n_p}$ with vertex set $V$. Denote each independent set of vertices $V_1,V_2,\dots ,V_p$ so that $V=V_1\cup V_2\cup \cdots \cup V_p$ and identify the $j$th vertex in $V_i$ by $x_i^j$.

Suppose first that $n_2\ge 2$. Partition the elements of ${\mathbb{Z}}_n$ into pairwise disjoint subsets $A_1,A_2,\dots ,A_p$ such that $\left|A_i\right|=n_i$ and ${\sum }_{a\in A_i}^{}a=\frac{n}{2}$ for every $1\le i\le p$. Such a partition exists by Theorem 5. Define $f:V\to {\mathbb{Z}}_n$ so that $f:V_i\to A_i$ is an arbitrary bijection for $i=1,2,\dots ,p$. The weight of any vertex $v\in V_i$ is $$w\left(x_i^j\right)=(p-1)\frac{n}{2}.$$Therefore, $f$ is a ${\mathbb{Z}}_n$-distance magic labeling and $G$ is ${\mathbb{Z}}_n$-distance magic.

Suppose on the other hand that $G$ is ${\mathbb{Z}}_n$-distance magic with (bijective) labeling $\ell$. If $n_2=1$, then $w\left(x_1^1\right)={\sum }_{g\in \mathbb{Z}n}^{}g-\ell \left(x_1^1\right)$ and $w\left(x_2^1\right)={\sum }_{g\in \mathbb{Z}n}^{}g-\ell \left(x_2^1\right)$, which implies $\ell \left(x_1^1\right)=\ell \left(x_2^1\right)$. But this contradicts the bijective property of $\ell$. Therefore, $n_2\ge 2$.□

Combined with Theorem 8, we have completed the classification of ${\mathbb{Z}}_n$-distance magic labelings of complete odd-partite graphs.

Theorem 10

Let $G=K_{n_1,n_2,\dots ,n_p}$ be a complete $p$-partite graph such that $p$ is odd, $1\le n_1\le n_2\le \cdots \le n_p$, and$n=n_1+n_2+\cdots +n_p$. The graph$G$ is${\mathbb{Z}}_n$-distance magic if and only if $n_2\ge 2$.

Proof

The proof is by Theorems 8 and 9.□

Next we turn our attention to complete even-partite graphs.

Theorem 11

Let $n=cp$ where$c$ is even and$p\ge 2$. The complete$p$-partite graph $K_{c,c,c,\dots ,c}$ is ${\mathbb{Z}}_n$-distance magic.

Proof

The proof follows from Theorem 7 in a similar way as Theorem 9 followed from Theorem 5, so we omit the details.□

4 Directed complete $p$-partite graphs

For directed graphs, the orientable ${\mathbb{Z}}_n$-distance magic classification of complete $p$-partite graphs is finished only for $p\le 3$ as the following theorem shows [4].

Theorem 12

[4] Let $G=K_{n_1,n_2,\dots ,n_p}$ be a complete $p$-partite graph with $1\le n_1\le n_2\le \cdots \le n_p$, and $n=n_1+n_2+\cdots +n_p$. If$p=1$,$G$ is orientable${\mathbb{Z}}_n$-distance magic if and only if $n$ is odd. If $p=2$,$G$ is orientable${\mathbb{Z}}_n$-distance magic if and only if $n⁄\equiv 2(mod4)$. If $p=3$,$G$ is orientable${\mathbb{Z}}_n$-distance magic for all $n_1,n_2,n_3$.

The authors of [4] cited [1] to obtain the following observation regarding complete $p$-partite graphs of odd order.

Observation 13

[4] Let $G=K_{n_1,n_2,\dots ,n_p}$ be a complete $p$-partite graph with $1\le n_1\le n_2\le \cdots \le n_p$, and $n=n_1+n_2+\cdots +n_p$, an odd number. If $n_2\ge 2$, then$G$ is orientable${\mathbb{Z}}_n$-distance magic.

From Theorem 5, we obtain the following new result.

Theorem 14

Let $G=K_{n_1,n_2,\dots ,n_p}$ be a complete $p$-partite graph with $1\le n_1\le n_2\le \cdots \le n_p$, and $n=n_1+n_2+\cdots +n_p$. If$p\ge 3$ is odd and$n_2\ge 2$, then$G$ is orientable${\mathbb{Z}}_n$-distance magic.

Proof

Let $G=K_{n_1,n_2,\dots ,n_p}$ with vertex set $V$. Denote each independent set of vertices $V_1,V_2,\dots ,V_p$ so that $V=V_1\cup V_2\cup \cdots \cup V_p$ and identify the $j$th vertex in $V_i$ by $x_i^j$. If $n$ is odd, $G$ is orientable ${\mathbb{Z}}_n$-distance magic by Observation 13, so we may assume from now on that $n$ is even.

Construct a ${\mathbb{Z}}_n$-distance magic labeling of $V$ using Theorem 9. Orient the edges of $G$ as follows. Let $H=K_p$ with vertex set $V\left(H\right)=\{x_1,x_2,\dots ,x_p\}$. Notice that since $p$ is odd, $H$ is Eulerian. Form the directed graph $\vec{H}$ by orienting the edges of $H$ to form a flow (all arcs are joined head to tail) along the Eulerian cycle. Necessarily, every vertex $x\in V\left(H\right)$ is adjacent to exactly $\frac{p-1}{2}$ heads of arcs and exactly $\frac{p-1}{2}$ tails of arcs. Now construct the directed graph $\vec{G}$ by orienting the edges of $G$ so that the edge $x_i^j{x}_k^l\in E\left(G\right)$ receives the same orientation as the corresponding edge $x_i{x}_k$ in $E\left(H\right)$.

The weight of any vertex $v\in V_i$ is now $$w\left(x_i^j\right)=\frac{(p-1)}{2}\frac{n}{2}-\frac{(p-1)}{2}\frac{n}{2}=0.$$Therefore, $f$ is an orientable ${\mathbb{Z}}_n$-distance magic labeling, and $G$ is orientable ${\mathbb{Z}}_n$-distance magic.□

We complete this section by applying Theorem 7 to directed graphs.

Theorem 15

Let $G=K_{c,c,\dots ,c}$ be a complete $p$-partite graph and $n=cp$. If$c$ is even and$p$ is odd, then$G$ is orientable${\mathbb{Z}}_n$-distance magic.

Proof

The proof follows from the ${\mathbb{Z}}_n$-distance magic labeling given in Theorem 11 and arguments similar to those in the proof of the previous theorem.□

Table 1 CSP(p) property classification for ${\mathbb{Z}}_n$

5 Conclusion

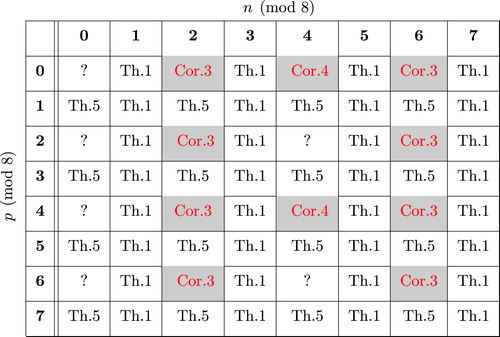
We have considered the following question. Given a positive integer $n$, for which partitions of $n=a_1+a_2+\cdots +a_p$ is it possible to partition the cyclic group ${\mathbb{Z}}_n$ into $p$ pairwise disjoint subsets $A_1,A_2,\dots ,A_p$ such that $\left|A_i\right|=a_i$, and ${\sum }_{a\in A_i}^{}a=t$, for some fixed element $t\in {\mathbb{Z}}_n$ and every $1\le i\le p?$ Table 1 summarizes for which (feasible) pairs $(n,p)$ we now have a complete answer. The cells shaded gray in the table reflect non-existence results and the cells that contain a “?” reflect open cases.