?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
The generalized crown is a well-known family of bipartite graphs whose order dimension is given in terms of the parameters
and
. In recent work, Garcia and Silva defined the notion of layering generalized crowns, producing multipartite posets called
-layered generalized crowns, whose order dimension is easily determined using
,
, and
. This paper extends the authors’ prior work on characterizing the associated graphs of critical pairs of generalized crowns, by providing a new and concrete description of an infinite family of graphs arising from critical pairs of the
-layered generalized crowns. Our main result gives a characterization of the adjacency matrices of these graphs. Through their associated posets with computable order dimension, these graphs have a strict upper bound on their chromatic number.
1 Introduction
Part of the rich history of computing the chromatic number of a graph includes a result of Felsner and Trotter who proved a connection between the order dimension of partially ordered sets and the chromatic number for certain associated graphs. In Citation[1], Felsner and Trotter proved that if is a poset and
is the associated graph of critical pairs of
, then
, thereby providing an upper bound on the chromatic number of the graphs
. Barrera-Cruz et al. Citation[2] proved that, in the case of a particular family of posets called crowns, the upper bound for the chromatic number of the associated graph is a tight bound. Equality is not known in the layered case, but the order dimension still provides an upper bound on the chromatic number of the associated graph. However, it is important to note that the existence of a strict upper bound on the chromatic number of a graph does not always yield complete information about the structure of the graph. For example, a trivial upper bound for the chromatic number of a graph is given by the number of vertices, yet this fact alone does not characterize the graph.
With the aim of concretely describing the associated graph of critical pairs, in Citation[3], we considered the graphs , where
is the generalized crown
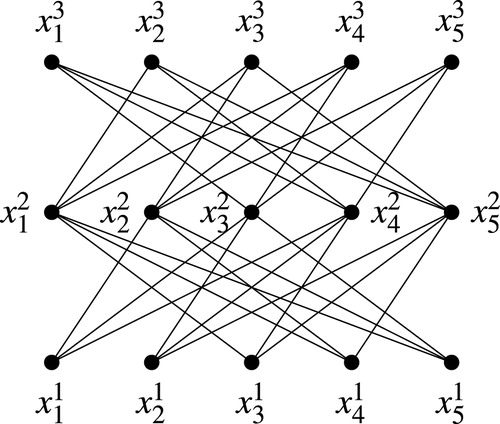
. We recall that the generalized crown
, as defined in Citation[4], is a height two poset with maximal elements
and minimal elements
. Each
is incomparable with
, and comparable over the remaining
elements. shows the Hasse diagram for the generalized crown
. In Citation[3], we provided a complete characterization of the infinite family of graphs
via their adjacency matrices was provided.
In this paper, we consider a natural extension of the work developed in Citation[3] by considering the graphs , where
is the
-layered generalized crown
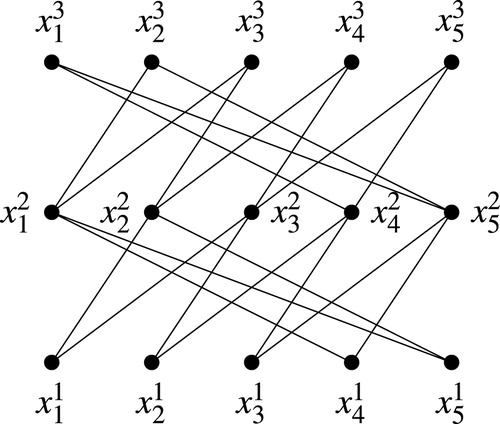
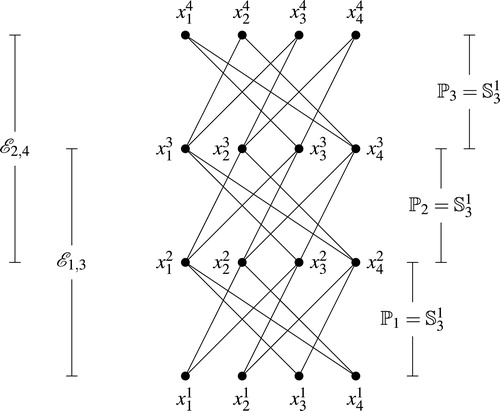
. The
-layered generalized crown was defined by Garcia and Silva in Citation[5] through the development of the operation of layering posets. The layering “…produces a larger poset from two compatible posets by gluing one poset above the other in a well-defined way” Citation[5]. The operation of layering generalized crowns produces a multipartite set, whose order dimension is easily computed. For an illustration of layering of generalized crowns see , which provides the Hasse diagram of the
-layered generalized crown
, which we denote by
.
Our main result gives a characterization of the graphs , where
is the
-layered generalized crown
, by completely and concretely describing the adjacency matrices of these graphs. Moreover, the computation of the matrices depends only on the values of
, and
. In Section 3 we characterize the adjacency matrices of the graphs
in the case where
and
. In Section 4 we consider the case where
and
. These sections thus provide a complete characterization of the adjacency matrices of the graphs
, where
is the
-layered generalized crown
, for all possible values of
and
.
2 Background
The definitions in this paper are consistent with those used in Citation[1,5–7].
Definition 1
Let be a set, called the ground set, and let
be a partial ordering on
with the following binary relations on
:
| 1. | reflexive: for all | ||||
| 2. | antisymmetry: if | ||||
| 3. | transitivity: if | ||||
Then the pair is a called poset or partially ordered set.
All ground sets considered in this paper are finite.
Example 1
Let be a finite set and let the ground set of our poset be the power set
. Consider a partial ordering on this set by containment of subsets. Then
forms a poset.
Notation 1
Let be a finite ground set and let
. We write
to denote that
is incomparable with
. We write
or
to denote that
lies over
in the partial ordering.
Our paper focuses on a special family of posets called -layered generalized crowns. We thus begin with the definition of a generalized crown, which was originally introduced by Trotter; see Citation[6].
Definition 2
Let with
and
. Then the generalized crown, denoted
, is a height 2 poset with
and
, where
| 1. |
| ||||
| 2. |
| ||||
Definition 3
Elements in the top row of the crown are called maximal elements and the set of all such elements is denoted by . Elements in the bottom row of the crown are called minimal elements and the set of minimal elements is denoted by
. Thus we have
for the ground set of the crown
.
We identify with
and
with
whenever
. This indexing scheme is called cyclic indexing.
We recall the definition of layering of posets introduced in Citation[5] by Garcia and Silva.
Definition 4
Let and
be two posets, such that there exists a bijection
. The
-layering of
over
is a poset
where
is the transitive closure of
In this process is literally glued with
. Since
is a bijection, there are no issues in doing so. In fact, this process can be repeated a finite number of times to obtain as many layers as desired.
Definition 5
The -layered generalized crown of
is denoted by
Notation 2
Elements in a layered generalized crown are denoted, where the subscript of each element denotes its location within a row and the superscript denotes its row. When considering
where
, we let
denote the set of elements in the
row (counting from bottom to top) of
, namely
. Note that in this case
.
Example 2
gives the Hasse diagram of the generalized crown and gives the Hasse diagram of the
-layered generalized crown
.
Definition 6
Let be a poset and let
. We say the strict downset of
is the set
and the strict upset of
is the set
Definition 7
Let be a poset and let
. We say that
is minimal if there does not exist
such that
. We say that
is maximal if there does not exist
such that
.
When the poset is understood we drop the subscript notation.
Definition 8
For a maximal element , the set of all minimal elements of
that are incomparable with
is denoted by
For a minimal element
, the set of all maximal elements of
that are incomparable to
is denoted by
The set of all incomparable pairs of is denoted by
Definition 9
Let be a poset and let
. We call
a critical pair if the following conditions hold:
| 1. |
| ||||
| 2. |
| ||||
| 3. |
| ||||
We let denote the set of all critical pairs of
. If
, then we say
is dual to
.
The next few definitions set the ground work for obtaining results concerning hypergraphs and graphs of -layered generalized crowns.
Definition 10
An alternating cycle in a poset is a sequence
of ordered pairs from
, where
in
(cyclically) for
.
We say an alternating cycle is strict when in
if and only if
(cyclically) for
.
Definition 11
A hypergraph is a set
of vertices along with a set
of edges which are subsets of
with size
. If an edge has size 2, it is called a graph edge. If an edge has size
, it is called a hyperedge. If a graph has only graph edges, then it is simply called a graph.
Definition 12
Given a hypergraph , we define the graph of
, to be
, where
.
Definition 13
Given a poset , the strict hypergraph of critical pairs of
, denoted
, is the hypergraph
, where
consists of subsets of
whose duals form strict alternating cycles. We let
denote the graph of
.
Definition 14
Given a graph with
, the adjacency matrix of
, denoted
, is defined by
As this paper concerns the characterization of the graphs via their adjacency matrix we introduce the following:
Definition 15
Let ,
and
. Then we let
, denote the adjacency matrix of the graph
.
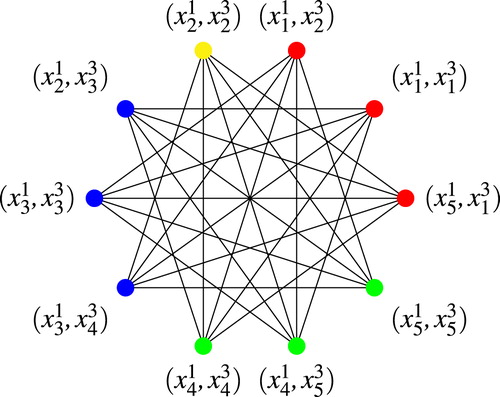
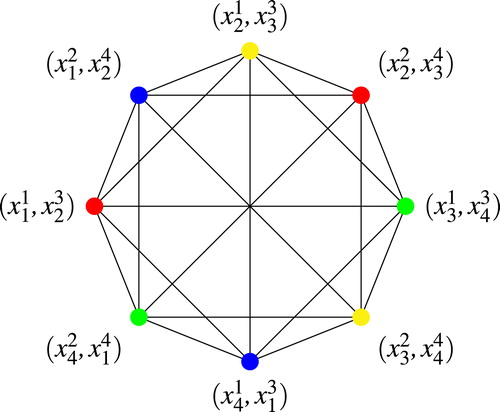
Example 3
depicts two layers of , that is
.
The critical pairs of are:
Using these critical pairs and the definition of a strict alternating cycle (of length two) we can compute the adjacency matrix, Table 1, and graph of
, .
In Citation[5, Theorem 4.3], Garcia and Silva proved that if and for
with
, then
. Applying this theorem we note that
. By applying the result of Felsner and Trotter, we know that
. Moreover, we recall a theorem in graph theory, which states that the chromatic number of a graph on
vertices satisfies
, where
is the cardinality of the maximal set of vertices that does not include adjacent vertices. In this case
and so
. Thus
, as denoted in .
Table 1 Adjacency matrix .
3 Characterizing 
 when
when 

In this section we assume and
. In these layered crowns, critical pairs can only be produced from elements in adjacent rows; see Citation[5, Lemma 4.1]. To make this precise it will be important to distinguish between the layers of the poset
. To do so we introduce the following:
Notation 3
For each , let
and for
, we let
and
. When
, we let
.
In the case where and
, the critical pairs of
arise only through adjacent rows
and
, where
. This occurs because
is large enough to compel an element of
to hit every element in
. To be precise, this means that for any
and
:
| • | If | ||||
Moreover, for any and
:
| • | If | ||||
By definition of , each adjacent set of rows (there are
such pairs) contributes
critical pairs to
. This is given by each of the
misses from each of the
nodes in a given pair of adjacent rows. Considering all of the adjacent pairs of rows yield the
critical pairs of
. We order these critical pairs using lexicographical order on their dual. This process yields a labeling for all of the rows/columns of the matrix
, which has dimensions
.
To simplify the computation of matrix , we decompose
into
submatrices each of size
as described below. First, for integers
, with
and
, we let
where the subscripts in the listing are taken cyclically modulo
. Then we let
Notice that for any
,
is an ordered listing of
critical pairs and hence
is an ordered listing of
critical pairs of
. Since
ranges between
and
, we know that
account for all
critical pairs of
.
Now for any two integers , we let
be the submatrix of
whose rows are labeled by
and whose columns are labeled by
. Therefore we write
Next we describe the submatrices of
, when
and
.
Lemma 1
Let ,
and
. If
is a submatrix of
where
, then
.
Proof
Suppose there exists a nonzero entry in where
. This implies there exists a strict alternating cycle of the form
where
and
are critical pairs in
and
, respectively. We note that since we are dealing with a general critical pair of the specified posets, for sake of simplicity, we omit the subscripts on these critical pairs. By definition of a strict alternating cycle, the following four conditions must hold:
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. |
| ||||
Since , without loss of generality we can assume that
. Observe that Condition 4. gives a contradiction since
and
but the elements of
are above those of
. Note that if the opposite inequality
is considered, then Condition 2. yields a contradiction. □
Lemma 2
Let and
. If
and
is a submatrix of
, then
where
and
are critical pairs of
and
, respectively.
Proof
Observe that is a strict alternating cycle provided that the following conditions are satisfied:
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. |
| ||||
Observe that Conditions 1. and 3. hold by definition of critical pairs. Condition 2. holds since . Now notice that the only comparable elements in
are
provided
. Namely if two elements in the same row are comparable, then they must be the same element. □
Lemma 3
Let and
. If
and
is a submatrix of
, then
, where
is the adjacency matrix of the graph
as described in Citation[3, Theorem 20].
Proof
By definition is the submatrix of
whose rows and columns are labeled by the critical pairs
where
These are exactly the critical pairs of the crown
at the
layer ordered by lexicographical order on their dual. These critical pairs and their ordering are identical (up to a shift in subscripts) to the critical pairs and ordering used in Citation[3, Theorem 20] to describe the adjacency matrix of the graph
, which is denoted
. Therefore the submatrix
for all
. □
Theorem 1
If and
, then
where the submatrices
are described as follows:
| • |
| ||||
| • |
| ||||
| • |
| ||||
The proof follows directly from Lemmas 1–3.
Example 4
The smallest example we can consider, which is an actual layered generalized crown, is , . We know that
is a 20 × 20 matrix and the submatrices
, where
, have dimension 10 × 10. So to compute
it suffices to compute
and
, as
and
.
First we recall that
and
Then we know that the submatrix
has rows and columns labeled by
, so using Lemma 3 and Citation[3, Theorem 20], we can compute that
is given by Table 2. Now by Lemma 2 we know that
has nonzero entries of
only at rows whose second entry in its label equals the first entry in the label of the column. Using this and the labeling given by
for rows and
by columns, we know that the submatrix
is given by Table 3. Therefore the adjacency matrix

Using the information from this adjacency matrix gives the graph .
Notice that by Citation[5, Theorem], , and hence
. Now notice that the graph
contains a few triangles between its vertices, for example between the vertices
,
, and
, hence
.
In fact is
-colorable as seen in .
Table 2 Submatrix of
.
Table 3 Submatrix of
.
4 Characterizing 
 when
when 

We break Section 4 into two subsections based upon the value of .
4.1 A small number of layers
In this section we consider the case where . In this setting, all critical pairs of
come from the extreme subposet
, as was shown in the proof of Citation[5, Theorem 4.3]. The extreme subposet
is the subposet of
generated by the set of minimal elements and maximal elements in
. The extreme subposet plays an important role in finding the critical pairs of
and consequently in characterizing the matrices
.
Theorem 2
Let and
. Then
, where
is the adjacency matrix of the graph
as described in Citation[3, Theorem 20].
Proof
By Citation[5, Theorem 4.3] the critical pairs of are exactly the critical pairs of the extreme subposet
. Moreover
, whenever
and
. Thus the adjacency matrix
as claimed. □
Observe that Example 3 satisfies all of the conditions of Theorem 2.
4.2 A large number of layers
Now we consider . In this case the critical pairs of
arise from various extreme subposets, as shown in the proof of Citation[5, Theorem 4.4]. We begin by setting some notation.
Notation 4
We adopt the notation used in the proof of Citation[5, Theorem 4.3]. Let
where
. Setting
, we let
, where
. From the proof of Citation[5, Theorem 4.3] we know that the critical pairs of
come from the incomparable elements in the subposets
. Hence
For , let
denote the elements of
ordered using lexicographical order on the dual of the critical pairs of
. For a fixed
, suppose
and
such that
in
. Then the index
must be a value in the set of cyclic indexing values:
Therefore, for ,
Let denote the submatrix of
whose rows are labeled by
and whose columns are labeled by
. Then we write
Lemma 4
Let ,
, and
. If
and
is a submatrix of
, then
.
Proof
By definition is the submatrix of
whose rows and columns are labeled by the elements of
, which are ordered using lexicographical order on their dual. These critical pairs are only arising from the extreme subposet of
, denoted
. By Citation[5, Theorem 4.3] we know that the extreme subposet
. Therefore the submatrix
, where
is the adjacency matrix of the graph
. □
Lemma 5
Let ,
, and
. If
and
is a submatrix of
such that
, then
where the integers
are taken modulo
.
Proof
Without loss of generality assume that . Let
, where
. Assume
and
. Then
forms a strict alternating cycle if and only if the following two conditions are satisfied:
(1)
(1) Using the fact that
, where
, Conditions (1) and (2) are (respectively) equivalent to:
(3)
(3)
Then Condition (3) holds since every element of
is comparable to every element of
. However, Condition (4) holds only when
. For
we compute the following information.
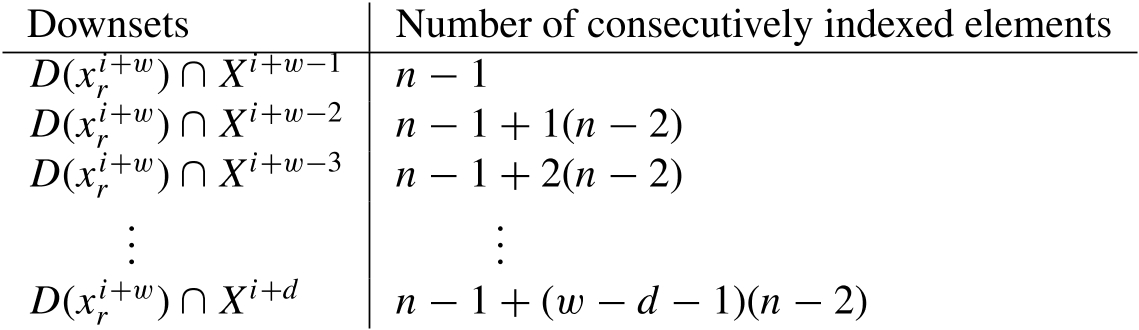
In fact
where the subscripts are taken modulo
. Therefore,
if and only if
Lemma 6
Let ,
, and
. If
and
is a submatrix of
such that
, then
Proof
Without loss of generality assume that . Assume
and
. Then
forms a strict alternating cycle if and only if the following two conditions are satisfied:
(5)
(5) Using the fact that
, Conditions (5) and (6) are (respectively) equivalent to:
(7)
(7) Then Condition (7) holds since every element of
is hit by (or is less than or equal) every element of
. However Condition (8) only holds when
, as expected. □
Lemma 7
Let ,
, and
. If
is a submatrix of
such that
, then
.
Proof
Without loss of generality we assume that and let
and
. Note that
will never form a strict alternating cycle since
and
, where
therefore
. This implies that no strict alternating cycles exist, and thus
, whenever
. □
We now give the main result in this section.
Theorem 3
If ,
, and
, then
where the submatrices
are described as follows:
| • |
| ||||
| • |
| ||||
| • |
| ||||
| • |
| ||||
The proof follows directly from Lemmas 4–7.
We demonstrate with an example how the matrix changes as more layers are added to a generalized crown.
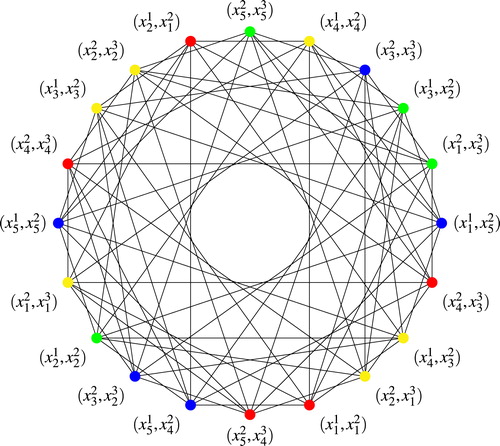
Example 5
In this example we begin with a detailed computation of and its associated graph
. We will then provide the matrices
and
and their associated graphs
and
, respectively.
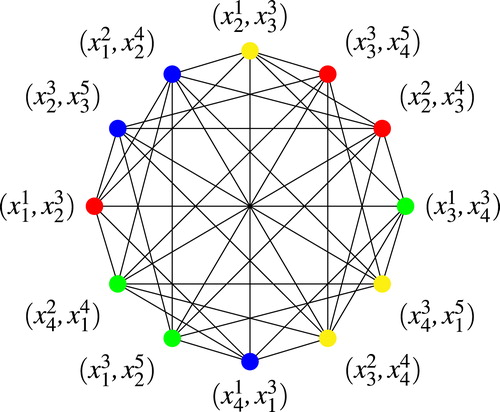
In this case the critical pairs arise from the extreme subposets and
, as depicted in . These critical pairs are as follows:
The eight critical pairs imply that
has dimension 8 × 8. As before, we label the rows/columns by using lexicographical ordering on the dual of the critical pairs. That is, the rows and columns will be labeled as follows:
To determine the non-zero entries of
we determine that from the above critical pairs the following sets form strict alternating cycles:
The above information is enough to give the graph
, depicted in , and its adjacency matrix
, as seen in Table 4. When we consider the
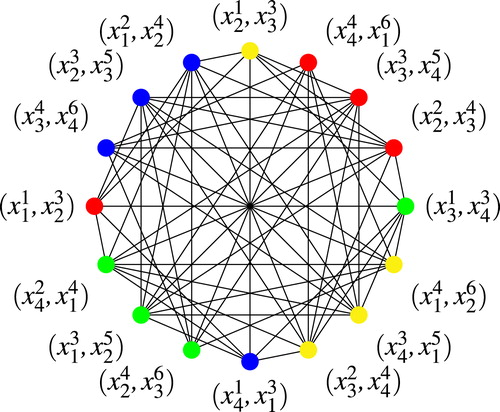
-layered crown
, we obtain
, as shown in Table 5 and the graph
is given in . From the
-layered crown
, we obtain
, as shown in Table 6 and the graph
, which is given in .
Table 4 .
Table 5 .
Table 6 .
We recall that Garcia and Silva proved Citation[5, Theorem 4.4]: For and for
with
, then
. Using this result and the fact that in our examples
, we note that
. Then by the result of Trotter and Felsner, Citation[1], the chromatic number of the graphs
,
, and
is less than or equal to
. In fact, all of these graphs contain
, the complete graph on four vertices, as a subgraph, hence they are in fact
-colorable and this is depicted in the respective graphs in .
Given the results in Citation[2], we conjecture that the chromatic number is equal to the order dimension computed in Citation[5] for layered generalized crowns.
Conjecture 1
Let be the
-layered generalized crown
. Then,
, where
is as given in Citation[5].
Acknowledgment
The authors extend their gratitude to the National Science Foundation Division of Mathematical Sciences (DMS-1045082) for travel support.
References
- FelsnerS.TrotterW.T., Dimension, graph and hypergraph coloring Order 17 2 2000 167–177
- Barrera-CruzF.GarciaR.E.HarrisP.E.KubikB.SmithH.C.TalbottS.TaylorL.TrotterW.T., The graph of critical pairs of a crown2019accepted to OrderarXiv:1708.06675
- GarciaR.E.HarrisP.E.KubikB.TalbottS., Block circulant graphs and the graphs of critical pairs of a crown2019submitted to Electronic Journal of Graph Theory and ApplicationsarXiv:1410.5087
- Trotter Jr.W.T., Dimension of the crown Snk Discrete Math. 81974 85–103
- GarciaR.E.SilvaD.A., Order dimension of layered generalized crowns Ars Combin. CXIIIA2014 117–186
- TrotterW.T., Combinatorics and partially ordered sets Johns Hopkins Series in the Mathematical SciencesDimension Theory1992Johns Hopkins University PressBaltimore, MD
- TrotterW.T., Partially ordered sets Handbook of Combinatorics, vol. 1, 21995Elsevier Sci. B. V.Amsterdam433–480