Identifying Hamilton cycles in the Cartesian product of directed cycles

Abstract

Let $G=C_{n_1}\square C_{n_2}\square \cdots \square C_{n_k}$ be a Cartesian product of $k\ge 2$ directed cycles. It is known that $G$ has a Hamilton cycle if there is a permutation $(n_1^{\prime },n_2^{\prime },\dots ,n_k^{\prime })$ of $(n_1,n_2,\dots ,n_k)$ that satisfies $gcd(n_i^{\prime },n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime })=s_i+z_i$ and $gcd(n_i^{\prime },s_i)=gcd(n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime },z_i)=1$ for some positive integers $s_i,z_i$, where $k>i\ge 1$. In addition, if $gcd(n_1^{\prime }\cdot n_2^{\prime }\cdots n_k^{\prime },s_1\cdot z_1)=1$ then $G$ has two arc-disjoint Hamilton cycles. We identify a Hamilton cycle and two arc-disjoint Hamilton cycles in $G$ in such cases.

Keywords:

• Cartesian product of directed cycles
• Hamilton cycle
• Hamiltonian digraph
• Hamiltonian decomposition

1 Introduction

In this paper we focus on the identification of Hamilton cycles in a Cartesian product of directed cycles, which satisfies certain conditions initially introduced by Trotter and Erdös [1] for two directed cycles about forty years ago, and extended in this paper to $k$ cycles, where $k\ge 2$. A Cartesian product $G=C_{n_1}\square C_{n_2}\square \cdots \square C_{n_k}$ of $k$ directed cycles $C_{n_1},C_{n_2},\dots$ $C_{n_k}$ is the digraph such that the vertex set $V\left(G\right)$ equals the Cartesian product $V\left(C_{n_1}\right)\times V\left(C_{n_2}\right)\times \cdots \times V\left(C_{n_k}\right)$ and there is an arc in $G$ from vertex $u=(u_1,u_2,\dots ,u_k)$ to vertex $v=(v_1,v_2,\dots ,v_k)$ if and only if there exists $1\le r\le k$ such that there is an arc $(u_r,v_r)$ in $C_{n_r}$ and $u_i=v_i$ for all $i\ne r$.

Trotter and Erdös proved the following:

Theorem 1.1

[1] The Cartesian product $C_{n_1}\square C_{n_2}$ of directed cycles is Hamiltonian if and only if $s=gcd(n_1,n_2)\ge 2$ and there exist positive integers $s_1,s_2$ so that $s_1+s_2=s$ and $gcd(n_1,s_1)=gcd(n_2,s_2)=1$.

Keating extended Trotter and Erdös theorem as follows:

Theorem 1.2

[2] The Cartesian product $C_{n_1}\square C_{n_2}$ of directed cycles has Hamiltonian decomposition if and only if$s=gcd(n_1,n_2)\ge 2$ and there exist positive integers $s_1,s_2$ so that $s_1+s_2=s$ and $gcd(n_1{n}_2,s_1{s}_2)=1$.

Furthermore, Curran and Witte extended result of Trotter and Erdös to the Cartesian product of $k$ directed cycles for $k\ge 3$.

Theorem 1.3

[3] There is a Hamilton circuit in the Cartesian product of any three or more nontrivial directed cycles.□

Based on Theorem 1.3 it is trivial to extend the sufficient conditions of Trotter and Erdös [1] for the existence of Hamilton cycle from the Cartesian product of 2 directed cycles to the Cartesian product of $k$ directed cycles for $k\ge 2$ as follows:

Theorem 1.4

Let $G=C_{n_1}\square C_{n_2}\square \cdots \square C_{n_k}$ be a Cartesian product of $k\ge 2$ directed cycles.$G$ has a Hamilton cycle if there is a permutation $(n_1^{\prime },n_2^{\prime },\dots ,n_k^{\prime })$ of $(n_1,n_2,\dots ,n_k)$ that satisfies $gcd(n_i^{\prime },n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime })=s_i+z_i$ and$gcd(n_i^{\prime },s_i)=gcd(n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime },z_i)=1$ for some positive integers $s_i,z_i$, where $k>i\ge 1$.

It is also trivial based on Theorem 1.3 to extend the sufficient conditions of Keating [2] for the existence of two arc-disjoint Hamilton cycles from the Cartesian product of 2 directed cycles to the Cartesian product of $k$ directed cycles for $k\ge 2$ as follows:

Theorem 1.5

Let $G=C_{n_1}\square C_{n_2}\square \cdots \square C_{n_k}$ be a Cartesian product of $k\ge 2$ directed cycles.$G$ has two arc-disjoint Hamilton cycles if there is a permutation $(n_1^{\prime },n_2^{\prime },\dots ,n_k^{\prime })$ of $(n_1,n_2,\dots ,n_k)$ that satisfies $gcd(n_1^{\prime }\cdot n_2^{\prime }\cdots n_k^{\prime },s_1\cdot z_1)=1$,$gcd(n_i^{\prime },n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime })=s_i+z_i$ and$gcd(n_i^{\prime },s_i)=gcd(n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime },z_i)=1$ for some positive integers $s_i,z_i$, where $k>i\ge 1$.

In this paper, we identify a Hamilton cycle in the Cartesian product of directed cycles $G$ when the sufficient conditions from Theorem 1.4 are satisfied for the existence of Hamilton cycle in $G$. In addition, we identify two arc-disjoint Hamilton cycles in $G$ when the sufficient conditions from Theorem 1.5 for their existence are satisfied. Related result was obtained in [4] where directed cycles of equal lengths were identified that decompose $G$.

2 Main results

Let $a_i$ be an arc induced by $C_{n_i}$ in the Cartesian product of directed cycles. Let $a_i^r$ denote a directed walk $W=\underset{r}{\underbrace{a_i{a}_i\cdots a_i}}$ from an arbitrary vertex in the Cartesian product of directed cycles represented by a sequence of $r$ arcs induced by $C_{n_i}$ for some positive integer $r$. In addition, let ${(a_i,a_j,\dots ,a_k)}^r$ denote a directed walk $W$ from an arbitrary vertex in the Cartesian product of directed cycles represented by a sequence of arcs $(a_i,a_j,\dots ,a_k)$ occurring sequentially $r$ times for some positive integer $r$. Hence, $W={(a_i,a_j,\dots ,a_k)}^r=\underset{sequence1}{\underbrace{a_i{a}_j\cdots a_k}}\underset{sequence2}{\underbrace{a_i{a}_j\cdots a_k}}\cdots \underset{sequencer}{\underbrace{a_i{a}_j\cdots a_k}}$.

Lemma 2.1

Let $n_1,n_2,s_1,s_2$ be positive integers such that $gcd(n_1,n_2)=s_1+s_2$ and $gcd(n_1,s_1)=gcd(n_2,s_2)=1$. Then$G=C_{n_1}\square C_{n_2}$ has a Hamilton cycle of form ${(a_1^{s_1},a_2^{s_2})}^r$ for some positive integer $r$.

Proof

Let $v_1=(0,0)$ and $v_{s_1+s_2+1}=(s_1,s_2)$. Then based on proof of Theorem 1.1 in [1] there is a path $P$ between $v_1$ and $v_{s_1+s_2+1}$ of form $P=v_1{v}_2\dots v_{s_1+s_2+1}=(0,0)(1,0)\dots (s_1,0)(s_1,1)(s_1,2)\dots (s_1,s_2)$ followed by the vertices using the rule $v_{i+s_1+s_2}=v_i+(s_1,s_2)$, which results in a Hamilton cycle in $G$. This implies based on our notation that $G$ has a Hamilton cycle of form ${(a_1^{s_1},a_2^{s_2})}^r$ for some positive integer r. □

Lemma 2.2

Let $n_1,n_2,s_1,s_2$ be positive integers such that $gcd(n_1,n_2)=s_1+s_2$ and $gcd(n_1{n}_2,s_1{s}_2)=1$. Then$G=C_{n_1}\square C_{n_2}$ can be decomposed into the Hamilton cycles of forms ${(a_1^{s_1},a_2^{s_2})}^r$ and ${(a_1^{s_2},a_2^{s_1})}^r$ for some positive integer r.

Proof

If $gcd(n_1{n}_2,s_1{s}_2)=1$ then $gcd(n_1,s_1)=gcd(n_2,s_2)=gcd(n_1,s_2)=gcd(n_2,s_1)=1$. So, by Lemma 2.1 there exist Hamilton cycles $H_1={(a_1^{s_1},a_2^{s_2})}^r$ and $H_2={(a_1^{s_2},a_2^{s_1})}^r$ for some positive integer $r$ in $G$. For vertex $v_1$, let $P_{v_1}^1=v_1{v}_2\cdots v_k$ and $P_{v_1}^2=v_1{w}_2\cdots w_k$ be two walks $v_1{(a_1^{s_1},a_2^{s_2})}^q$ and $v_1{(a_1^{s_2},a_2^{s_1})}^q$ for some positive integer $q$, respectively. Let $t$ be the smallest positive integer for which $v_t=w_t$. This implies either paths $v_{t-1}{v}_t=v_{t-1}{a}_1{v}_t$, $w_{t-1}{w}_t=w_{t-1}{a}_2{w}_t$ or paths $v_{t-1}{v}_t=v_{t-1}{a}_2{v}_t$, $w_{t-1}{w}_t=w_{t-1}{a}_1{w}_t$ are included in $P_{v_1}^1$ and $P_{v_1}^2$, respectively. By induction, for every vertex $v_i$, $i\ge t$, there are paths $v_{i-1}{v}_i=v_{i-1}{a}_j{v}_i$, $w_{i-1}{w}_i=w_{i-1}{a}_{3-j}{w}_i$ included in $P_{v_1}^1$ and $P_{v_1}^2$, where $j=1$ or $j=2$. This implies that $H_1$ and $H_2$ are arc-disjoint.□

To present our main results we need additional definitions as follows. Let $b_i^j$ denote $j$ first arcs of a Hamilton cycle $C_G$ in $G=C_{n_i}\square C_{n_{i+1}}\square \cdots \square C_{n_{i+k-1}}$, starting from an arbitrary arc in $C_G$. Furthermore, let ${\left(b_i^j\right)}^r$ denote $r$ consecutive sequences, each of $j$ consecutive arcs, in $C_G$ starting from an arbitrary arc in $C_G$. Hence, $r$’th sequence of arcs starts with $r\cdot j+1$ arc and ends with $r\cdot j+j$ arc, taken module $n_i\cdot n_{i+1}\cdots n_{i+k-1}$ plus one, in a Hamilton cycle from an arbitrary arc in $C_{n_i}\square C_{n_{i+1}}\cdots C_{n_{i+k-1}}$. Consequently, a directed walk $W={(a_i^{s_i},b_i^{z_i})}^{r_i}$ represents the following sequence of arcs: $W={(a_i^{s_i},b_i^{z_i})}^{r_i}=\underset{seq.1:s_{i}arcs}{\underbrace{a_i{a}_i\cdots a_i}}\underset{seq.1:z_{i}arcs}{\underbrace{b_i{b}_i\cdots b_i}}\cdots \underset{seq.r_i:s_{i}arcs}{\underbrace{a_i{a}_i\cdots a_i}}\underset{seq.r_i:z_{i}arcs}{\underbrace{b_i{b}_i\cdots b_i}}$ in $G$.

W can now state the following result for identification of a Hamilton cycle in $G$.

Theorem 2.3

Let $G=C_{n_1}\square C_{n_2}\square \cdots \square C_{n_k}$ be a Cartesian product of $k\ge 2$ directed cycles. If $(n_1^{\prime },n_2^{\prime },\dots ,n_k^{\prime })$ is a permutation of $(n_1,n_2,\dots ,n_k)$ that satisfies $gcd(n_i^{\prime },n_{i+1}^{\prime }{n}_{i+2}^{\prime }\cdots n_k^{\prime })=s_i+z_i$ and $gcd(n_i^{\prime },s_i)=gcd(n_{i+1}^{\prime }{n}_{i+2}^{\prime }\cdots n_k^{\prime },z_i)=1$ for some positive integers $s_i,z_i$, where $k>i\ge 1$, then$G$ has a Hamilton cycle of form $C_G={(a_1^{s_1},b_1^{z_1})}^r$ for some positive integer $r$.

Proof

If $k=2$ then based on our definition $b_1^{z_1}$ denotes $z_1$ consecutive arcs of type $a_2$ in our Hamilton cycle. So, ${(a_1^{s_1},b_1^{z_1})}^r={(a_1^{s_1},a_2^{z_1})}^r$, and by setting $z_1=s_2$ we obtain our Hamilton cycle $C_G$ according to Lemma 2.1. For induction hypothesis, assume $gcd(n_i,n_{i+1}{n}_{i+2}\cdots n_k)=s_i+z_i$, $gcd(n_i,s_i)=gcd(n_{i+1}{n}_{i+2}\cdots n_k,z_i)=1$ and $C_G={(a_2^{s_2},b_2^{z_2})}^{r_2}$ are satisfied for some positive integers $r_2,s_i,z_i$, where $k>i\ge 2$. Let $n_1$ be an integer such that $gcd(n_1,n_2{n}_3\cdots n_k)=s_1+z_1$ and $gcd(n_1,s_1)=gcd(n_2{n}_3\cdots n_k,z_1)=1$ for some positive integers $s_1,z_1$. Since $C_G={(a_2^{s_2},b_2^{z_2})}^{r_2}$ exists then $G^{\prime }=C_{n_1}\square C_{n_2}\square \cdots \square C_{n_k}$ contains a spanning directed Cartesian product of directed cycles $H=C_{n_1}\square C_{n_2\cdot n_3\cdots n_k}$. Consequently, by Lemma 2.1 $G^{\prime }$ has a Hamilton cycle and $C_{G^{\prime }}={(a_1^{s_1},b_1^{z_1})}^{r_1}$ is satisfied for some positive integer $r_1$.□

Finally, we can identify two arc-disjoint Hamilton cycles in $G=C_{n_1}\square C_{n_2}\square \cdots \square C_{n_k}$ according to the following theorem.

Theorem 2.4

Let $G=C_{n_1}\square C_{n_2}\square \cdots \square C_{n_k}$ be a Cartesian product of $k\ge 2$ directed cycles. If $(n_1^{\prime },n_2^{\prime },\dots ,n_k^{\prime })$ is a permutation of $(n_1,n_2,\dots ,n_k)$ that satisfies $gcd(n_1^{\prime }\cdot n_2^{\prime }\cdots n_k^{\prime },s_1\cdot z_1)=1$,$gcd(n_i^{\prime },n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime })=s_i+z_i$ and$gcd(n_i^{\prime },s_i)=gcd(n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime },z_i)=1$ for some positive integers $s_i,z_i$, where $k>i\ge 1$, then$G$ has two arc-disjoint Hamilton cycles of form $C_G^1={(a_1^{s_1},b_1^{z_1})}^r$ and $C_G^2={(a_1^{z_1},b_1^{s_1})}^r$ for some positive integer $r$.

Proof

If $k=2$ then by Lemma 2.2 the conditions in our hypothesis are sufficient for decomposition of $G$ into the Hamilton cycles of forms ${(a_1^{s_1},b_1^{s_2})}^r$ and ${(a_1^{s_2},b_1^{s_1})}^r$ for some positive integer r, where $b_1=a_2$. Otherwise, if $k\ge 3$ then by the same argument as in proof of Theorem 2.3, because the sufficient conditions of Theorem 2.3 are satisfied, for some permutation $(n_1^{\prime },n_2^{\prime },\dots ,n_k^{\prime })$ $G$ contains a spanning Cartesian product of directed cycles $G^{\prime }=C_{n_1^{\prime }}\square C_{n_2^{\prime }\cdot n_3^{\prime }\cdots n_k^{\prime }}=C_{n_1^{\prime }}\square C_{n_2^{”}}$ that satisfies $gcd(n_1^{\prime },n_2^{”})=s_1+z_1$ and $gcd(n_1^{\prime },s_1)=gcd(n_2^{”},z_1)=1$ for some positive integers $s_1,z_1$. Hence, if $gcd(n_1^{\prime }\cdot n_2^{”},s_1\cdot z_1)=1$, which is equivalent to $gcd(n_1^{\prime }\cdot n_2^{\prime }\cdots n_k^{\prime },s_1\cdot z_1)=1$, then by Lemma 2.2 $G$ contains two arc-disjoint Hamilton cycles of forms ${(a_1^{s_1},b_1^{z_1})}^r$ and ${(a_1^{z_1},b_1^{s_1})}^r$ for some integer $r\ge 1$.□

3 Identification of explicit Hamilton cycle

Based on Theorem 2.3 (Theorem 2.4, respectively) we can identify a Hamilton cycle (two arc-disjoint Hamilton cycles, respectively) in $G=C_{n_1^{\prime }}\square C_{n_2^{\prime }}\square \cdots \square C_{n_k^{\prime }}$ as follows. Step 1: Identify a Hamilton cycle for $C_{n_{k-1}^{\prime }}\square C_{n_k^{\prime }}$ according to Theorem 2.3; Step 2: For every consecutive Hamilton cycle in the series of the Cartesian products of cycles $$(C_{n_{k-1}^{\prime }}\square C_{n_k^{\prime }},C_{n_{k-2}^{\prime }}\square C_{n_{k-1}^{\prime }}\square C_{n_k^{\prime }},\dots ,C_{n_2^{\prime }}\square C_{n_3^{\prime }}\square \cdots \square C_{n_k^{\prime }})$$identify the successive Hamilton cycles in the series of the Cartesian products of cycles $$(C_{n_{k-2}^{\prime }}\square C_{n_{k-1}^{\prime }}\square C_{n_k^{\prime }},C_{n_{k-3}^{\prime }}\square C_{n_{k-2}^{\prime }}\square C_{n_{k-1}^{\prime }}\square C_{n_k^{\prime }},\dots ,C_{n_1^{\prime }}\square C_{n_2^{\prime }}\square \cdots \square C_{n_k^{\prime }}).$$Hence, a Hamilton cycle in $C_{n_i^{\prime }}\square C_{n_{i+1}^{\prime }}\square \cdots \square C_{n_k^{\prime }}$ is identified based on Theorem 2.3 and based on a Hamilton cycle in $C_{n_{i+1}^{\prime }}\square C_{n_{i+2}^{\prime }}\square \cdots \square C_{n_k^{\prime }}$ for every $i$, where $k-1>i\ge 1$. In addition, a pair of Hamilton cycles in $C_{n_1^{\prime }}\square C_{n_2^{\prime }}\square \cdots \square C_{n_k^{\prime }}$ is identified based on a Hamilton cycle in $C_{n_2^{\prime }}\square C_{n_3^{\prime }}\square \cdots \square C_{n_k^{\prime }}$ and based on Theorem 2.4.

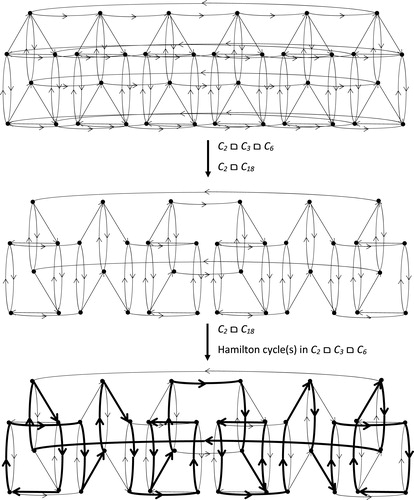
The following example illustrates identification of a Hamilton cycle and two arc-disjoint Hamilton cycles according to our approach in $C_2\square C_3\square C_6$.

Top digraph in Fig. 1 represents a Cartesian product of directed cycles $G=C_2\square C_3\square C_6$. For $G^{\prime }=C_3\square C_6$ we have $gcd(3,6)=3=s_2+z_2$. By setting $s_2=2,z_2=1$ we obtain $gcd(3,s_2)=gcd(6,z_2)=1$. Hence, by Theorem 2.3 there is a Hamilton cycle of form ${(a_2^{s_2},a_3^{z_2})}^{r_1}={(a_2^2,a_3)}^6$ in $G^{\prime }$. This implies that we obtain a spanning Cartesian product $G”=C_2\square C_{18}$ of $G$ illustrated in the middle digraph of Fig. 1. This is the last spanning subdigraph of $G$ in our procedure, and from this $G”$ we obtain a Hamilton cycle of form ${(a_1^{s_1},b_1^{z_1})}^{r_2}={(a_1,b_1)}^{18}$ based on Theorem 2.3 for $s_1=z_1=1$ because $gcd(2,18)=2=s_1+z_1$ and $gcd(2,s_1)=gcd(18,z_1)=1$. This Hamilton cycle is illustrated in the bottom digraph of Fig. 1 with thick arrows. Furthermore, since $gcd(2\cdot 18,s_1\cdot z_1)=1$ then by Theorem 2.4 $G$ contains two arc-disjoint Hamilton cycles. The second one is also illustrated in the bottom digraph of Fig. 1 with thin arrows.

Fig. 1 Identification of Hamilton cycle(s) in $C_2\square C_3\square C_6$.

Finally, consider the time complexity of establishing a Hamilton cycle based on our procedure. If the conditions of Theorem 2.3 are satisfied, then the time complexity for identifying a Hamilton cycle in any Cartesian product of directed cycles is as follows. For each permutation $(n_1^{\prime },n_2^{\prime },\dots ,n_k^{\prime })$ of $(n_1,n_2,\dots ,n_k)$ we calculate $gcd(n_i^{\prime },n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime })$ and for each $gcd(n_i^{\prime },n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime })$ we calculate at most $n_i^{\prime }$ expressions $gcd(n_i^{\prime },s_i)$ and $gcd(n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime },z_i)$ because $gcd(n_i^{\prime },n_{i+1}^{\prime }\cdot n_{i+2}^{\prime }\cdots n_k^{\prime })=s_i+z_i$ for some positive integers $s_i,z_i$, where $i=1,2,\dots ,k-1$ . Recall that for two integers $a,b$ Euclid’s algorithm can determine $gcd(a,b)$ in $\mathcal{O}(logmin(a,b))$. Denote $n_{max}=max(n_1,n_2,\dots ,n_k)$. Since there are $k!$ permutations of $(n_1,n_2,\dots ,n_k)$ then the time complexity required for identifying a Hamilton cycle in the Cartesian product of $k$ cycles is $\mathcal{O}(k!(k-1)(log{n}_{max}+2n_{max}log{n}_{max}))=\mathcal{O}(k!k{n}_{max}log{n}_{max})$.