The chromatic distinguishing index of certain graphs

Abstract

The distinguishing index of a graph $G$, denoted by $D^{\prime }\left(G\right)$, is the least number of labels in an edge coloring of $G$ not preserved by any non-trivial automorphism. The distinguishing chromatic index ${\chi }_D^{\prime }\left(G\right)$ of a graph $G$ is the least number $d$ such that $G$ has a proper edge coloring with $d$ labels that is preserved only by the identity automorphism of $G$. In this paper we compute the distinguishing chromatic index for some specific graphs. Also we study the distinguishing chromatic index of corona product and join of two graphs.

Keywords:

• Distinguishing index
• Edge colorings
• Chromatic index

1 Introduction

Let $G=(V,E)$ be a simple graph and $\mathrm{Aut}\left(G\right)$ denote the automorphism group of $G$. For $v\in V$, the neighborhood of $v$ is the set $N_G\left(v\right)=\{u\in V\left(G\right):uv\in E\left(G\right)\}$. The degree of $v$ in a graph $G$, denoted by ${deg}_G\left(v\right)$, is the number of edges of $G$ incident with $v$. In particular, ${deg}_G\left(v\right)$ is the number of neighbors of $v$ in $G$. Also, the maximum degree of $G$ is denoted by $\Delta \left(G\right)$.

A proper edge coloring $c$ of a nonempty graph $G$ (a graph with edges) is a function $c:E\left(G\right)\to S$, where $S$ is a set of labels (colors), with the property that $c\left(e\right)\ne c\left(f\right)$ for every two adjacent edges $e$ and $f$ of $G$. If the labels are chosen from a set of $k$ labels, then $c$ is called a proper $k$-edge coloring of $G$. The minimum positive integer $k$ for which $G$ has a proper $k$-edge coloring is called the chromatic index of $G$ and is denoted by ${\chi }^{\prime }\left(G\right)$. As a result of Vizing’s theorem, the chromatic index of every nonempty graph $G$ is one of two numbers, namely $\Delta \left(G\right)$ or $\Delta \left(G\right)+1$. A graph $G$ with ${\chi }^{\prime }\left(G\right)=\Delta \left(G\right)$ is called a class one graph while a graph $G$ with ${\chi }^{\prime }\left(G\right)=\Delta \left(G\right)+1$ is called a class two graph. For instance, it is proved that, $K_n$ is a class one graph if $n$ is even and is a class two graph if $n$ is odd, and also every regular graph of odd order is a class two graph. The next two results are about graphs who are class one.

Theorem 1.1

[1] Every bipartite graph is a class one graph.

Corollary 1.2

[2] If $G$ is a graph in which no two vertices of maximum degree are adjacent, then$G$ is a class one graph.

A proper vertex coloring of a graph $G$ is a function $c:V\left(G\right)\to S$, such that $c\left(u\right)\ne c\left(v\right)$ for every pair $u$ and $v$ of adjacent vertices of $G$. If $\left|S\right|=k$, then $c$ is called a proper$k$-vertex coloring of $G$. The minimum positive integer $k$ for which G has a proper $k$-vertex coloring is called the chromatic number of $G$ and is denoted by $\chi \left(G\right)$.

A coloring of $G$, $\varphi :V\to \{1,2,\dots ,r\}$, is said to be $r$-distinguishing, if no non-trivial automorphism of $G$ preserves all of the vertex labels. The point of the labels on the vertices is to destroy the symmetries of the graph, that is, to make the automorphism group of the labeled graph trivial. Formally, $\varphi$ is $r$-distinguishing if for every non-trivial $\sigma \in \mathrm{Aut}\left(G\right)$, there exists $x$ in $V$ such that $\varphi \left(x\right)\ne \varphi \left(\sigma \left(x\right)\right)$. Authors often refer to a coloring as a coloring, but there is no assumption that adjacent vertices get different colors. Of course the goal is to minimize the number of colors used. Consequently the distinguishing number of a graph $G$ is defined by $$D\left(G\right)=min\left\{r\right|G\mathit{has}\mathit{a}\mathit{coloring}\mathit{that}\mathit{is}\mathit{r}\text{-}\mathit{distinguishing}\}.$$

This number has been defined in [3]. If a graph has no nontrivial automorphisms, its distinguishing number is $1$. In other words, $D\left(G\right)=1$ for the asymmetric graphs. The other extreme, $D\left(G\right)=\left|V\left(G\right)\right|$, occurs if and only if $G=K_n$. Collins and Trenk [4] defined the distinguishing chromatic number ${\chi }_D\left(G\right)$ of a graph $G$ for proper colorings, so ${\chi }_D\left(G\right)$ is the least number $d$ such that $G$ has a proper coloring with $d$ labels that is only preserved by the trivial automorphism. Similar to this definition, Kalinowski and Pilśniak [5] have defined the distinguishing index $D^{\prime }\left(G\right)$ of $G$ which is the least integer $d$ such that $G$ has an edge coloring with $d$ colors that is preserved only by a trivial automorphism. The distinguishing index and number of some examples of graphs were exhibited in [3,5]. For instance, $D\left(P_n\right)=D^{\prime }\left(P_n\right)=2$ for every $n⩾3$, and $D\left(C_n\right)=D^{\prime }\left(C_n\right)=3$ for $n=3,4,5$, $D\left(C_n\right)=D^{\prime }\left(C_n\right)=2$ for $n⩾6$. It is easy to see that the value $|D\left(G\right)-D^{\prime }\left(G\right)|$ can be large. For example $D^{\prime }\left(K_{p,p}\right)=2$ and $D\left(K_{p,p}\right)=p+1$, for $p\ge 4$. A symmetric tree, denoted by $T_{h,d}$, is a tree with a central vertex $v_0$, all leaves at the same distance $h$ from $v_0$ and all the vertices which are not leaves with degree $d$. A bisymmetric tree, denoted by $T_{h,d}^{\prime \prime }$, is a tree with a central edge $e$, all leaves at the same distance $h$ from $e$ and all the vertices which are not leaves with degree $d$. The following theorem gives upper bounds for $D^{\prime }\left(G\right)$ based on the maximum degree of $G$.

Theorem 1.3

[5,6]

(i)	If $G$ is a connected graph of order $n\ge 3$, then $D^{\prime }\left(G\right)\le \Delta \left(G\right)$, unless $G$ is $C_3$, $C_4$ or $C_5$.
(ii)	Let $G$ be a connected graph that is neither a symmetric nor a bisymmetric tree. If $\Delta \left(G\right)\ge 3$, then $D^{\prime }\left(G\right)\le \Delta \left(G\right)-1$, unless $G$ is $K_4$ or $K_{3,3}$.

Also, Kalinowski and Pilśniak [5] defined the distinguishing chromatic index ${\chi }_D^{\prime }\left(G\right)$ of a graph $G$ as the least number $d$ such that $G$ has a proper edge coloring with $d$ labels that is preserved only by the identity automorphism of $G$.

Theorem 1.4

[5] If $G$ is a connected graph of order $n\ge 3$, then${\chi }_D^{\prime }\left(G\right)\le \Delta \left(G\right)+1$, except for four graphs of small order $C_4$,$K_4$,$C_6$,$K_{3,3}$.

This theorem immediately implies the following interesting result. A proper edge coloring of $G$ with ${\chi }^{\prime }\left(G\right)$ colors is called minimal.

Theorem 1.5

[5] Every connected class 2 graph admits a minimal edge coloring that is not preserved by any nontrivial automorphism.

We need the following results.

Theorem 1.6

[4] If $T$ is a tree of order $n\ge 3$, then$D^{\prime }\left(T\right)\le \Delta \left(T\right)$. Moreover, equality is achieved if and only if $T$ is either a symmetric or a path of odd length.

Theorem 1.7

[5] If $T$ is a tree of order $n\ge 3$, then ${\chi }_D^{\prime }\left(T\right)=\Delta \left(T\right)+1$, if and only if $T$ is a bisymmetric tree.

In the next section, we compute the distinguishing chromatic index of certain graphs such as friendship and book graphs. More precisely, we present a table of results that shows the chromatic index, the distinguishing index and the distinguishing chromatic index for various families of connected graphs. Also we obtain a relationship between the chromatic distinguishing number of line graph $L\left(G\right)$ of graph $G$ and the chromatic distinguishing index of $G$. In Section 3, we study the distinguishing chromatic index of join and corona product of two graphs.

2 The distinguishing chromatic index of certain graphs

Observation 2.1

(i)	For any graph $G$, ${\chi }_D^{\prime }\left(G\right)\ge max\{{\chi }^{\prime }\left(G\right),D^{\prime }\left(G\right)\}$.
(ii)	If $G$ has no non-trivial automorphisms, then ${\chi }_D^{\prime }\left(G\right)={\chi }^{\prime }\left(G\right)$ and $D^{\prime }\left(G\right)=1$. Hence ${\chi }_D^{\prime }\left(G\right)$ can be much larger than $D^{\prime }\left(G\right)$.

By this observation and Theorem 1.4 we can conclude that for any connected graph $G$ of order $n\ge 3$ and maximum degree $\Delta$, ${\chi }_D^{\prime }\left(G\right)$ is $\Delta$ or $\Delta +1$, except for $C_4$, $K_4$, $C_6$, $K_{3,3}$. In the latter case, ${\chi }_D^{\prime }\left(G\right)=\Delta +2$. Hence, for any connected graph $G$ we have $|{\chi }_D^{\prime }\left(G\right)-{\chi }^{\prime }\left(G\right)|\le 2$, and equality is only achieved for $C_4$, $K_4$, $C_6$, and $K_{3,3}$. By Theorem 1.5, it can be seen that ${\chi }_D^{\prime }\left(G\right)={\chi }^{\prime }\left(G\right)$, for class 2 graphs. In the following theorem we present a family of class 1 graphs such that ${\chi }_D^{\prime }\left(G\right)={\chi }^{\prime }\left(G\right)$.

Theorem 2.2

Let $G$ be a class one graph, i.e., ${\chi }^{\prime }\left(G\right)=\Delta \left(G\right)$. If there exists a vertex $x$ of $G$ for which$f\left(x\right)=x$ for all automorphisms $f$ of $G$, then${\chi }_D^{\prime }\left(G\right)=\Delta \left(G\right)$.

Proof

By contradiction suppose that ${\chi }_D^{\prime }\left(G\right)=\Delta \left(G\right)+1$. Then, for any proper $\Delta \left(G\right)$-coloring $c$ of $G$, there exists a nonidentity automorphism $f$ of $G$ preserving the coloring $c$. By hypothesis, we have $f\left(x\right)=x$. Since the incident edges to $x$ have different labels, so $f$ fixes every adjacent vertex to $x$, because $f$ preserves the coloring $c$. By the same argument for every adjacent vertex to $x$, we can conclude that $f$ is the identity automorphism, which is a contradiction.□

By Theorems 1.3, 1.4 and 1.7, we can characterize all connected graphs with ${\chi }_D^{\prime }\left(G\right)=D^{\prime }\left(G\right)$.

Theorem 2.3

Let $G$ be a connected graph of order $n\ge 3$ and maximum degree $\Delta$.

(i)	There is no connected graph $G$ with ${\chi }_D^{\prime }\left(G\right)=D^{\prime }\left(G\right)=\Delta +2$.
(ii)	${\chi }_D^{\prime }\left(G\right)=D^{\prime }\left(G\right)=\Delta +1$, if and only if $G\in \{C_3,C_4,C_5\}$.
(iii)	${\chi }_D^{\prime }\left(G\right)=D^{\prime }\left(G\right)=\Delta$, if and only if $G$ is a tree which is not a bisymmetric tree.

Here, we want to obtain the distinguishing chromatic index of complete bipartite graphs. Before we obtain the distinguishing chromatic index of complete bipartite graphs we need the following information of [7]: A coloring with $c$ labels of the edges of a complete bipartite graph $K_{s,t}$ having parts $X$ of size $s$ and $Y$ of size $t$ corresponds to a $t\times s$ matrix with entries from $\{1,\dots ,c\}$. The $i,j$ entry of the matrix is $k$ whenever the edge between the $i$th vertex in $Y$ and the $j$th vertex in $X$ has label $k$. We call this the bipartite adjacency matrix. For edge labeled complete bipartite graphs, the parts $X$ and $Y$ map to themselves if $\left|X\right|\ne \left|Y\right|$. In this case, if $A$ is the bipartite adjacency matrix, then an automorphism corresponds to selecting permutation matrices $P_Y$ and $P_X$ such that $A=P_{Y}A{P}_X$. If $\left|X\right|=\left|Y\right|$ then we also have automorphisms of the form $A=P_Y{A}^T{P}_X$. For any matrix with entries from $\{1,\dots ,c\}$ the degree of a column is a $c$-tuple $(x_1,\dots ,x_c)$ with $x_i$ equal to the number of entries that are $i$ in the column.

Theorem 2.4

[7] Let $A$ be the adjacency matrix of a $c$-edge labeled complete bipartite graph.

(i)	If there are two identical rows in $A$, then $A$ is not an identity coloring.
(ii)	If $A$ is not square and if the columns of $A$ have distinct degrees and the rows are distinct, then $A$ is an identity coloring. If $A$ is square, has distinct rows, distinct column degrees and the multiset of column degrees is different from the multiset of row degrees then $A$ is an identity coloring.

Theorem 2.5

The distinguishing chromatic index of complete bipartite graph$K_{s,t}$ where$s>t$, is${\chi }_D^{\prime }\left(K_{s,t}\right)=s$.

Proof

Let $A$ be the following $s\times t$ adjacency matrix of a $s$-edge labeled complete bipartite graph, $$A=\left(\begin{array}{cccccc}\hfill 1\hfill & \hfill 2\hfill & \hfill 3\hfill & \hfill \cdots \hfill & \hfill s-1\hfill & \hfill s\hfill \\ \hfill s\hfill & \hfill 1\hfill & \hfill 2\hfill & \hfill \cdots \hfill & \hfill s-2\hfill & \hfill s-1\hfill \\ \hfill s-1\hfill & \hfill s\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill s-3\hfill & \hfill s-2\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill t\hfill & \hfill t+1\hfill & \hfill t+2\hfill & \hfill \cdots \hfill & \hfill t-2\hfill & \hfill t-1\hfill \end{array}\right).$$Then it is clear that $A$ is a proper edge coloring. By Theorem 2.4(ii), it can be concluded that $A$ is a distinguishing coloring. In fact, the rows of $A$ are distinct, and since the number of label $t+i-1\left(mods\right)$ in the $i$th column is one and in the $j$th column, $j\ne i$, is zero, so the columns have distinct degrees. Hence ${\chi }_D^{\prime }\left(K_{s,t}\right)=s$.□

Before we prove the next result, we need the following preliminaries: By the result obtained by Fisher and Isaak [7] and independently by Imrich, Jerebic and Klavžar [8] the distinguishing index of complete bipartite graphs is as follows.

Theorem 2.6

[7,8] Let $p,q,r$ be integers such that $r\ge 2$ and ${(r-1)}^p<q\le r^p$ . Then $$D^{\prime }\left(K_{p,q}\right)=\left\{\begin{array}{cc}r\hfill & \text{if}q\le r^p-\lceil {log}_{r}p\rceil -1,\hfill \\ r+1\hfill & \text{if}q\ge r^p-\lceil {log}_{r}p\rceil +1.\hfill \end{array}\right.$$If $q=r^p-\lceil {log}_{r}p\rceil$ then the distinguishing index $D^{\prime }\left(K_{p,q}\right)$ is either $r$ or$r+1$ and can be computed recursively in $O(log\left(q\right))$ time.

The friendship graph $F_n$ $(n⩾2)$ can be constructed by joining $n$ copies of the cycle graph $C_3$ with a common vertex.

Theorem 2.7

[9] Let $a_n=1+27n+3\sqrt{81n^2+6n}$. For every $n\ge 2$, $$D^{\prime }\left(F_n\right)=\lceil \frac{1}{3}{\left(a_n\right)}^{\frac{1}{3}}+\frac{1}{3{\left(a_n\right)}^{\frac{1}{3}}}+\frac{1}{3}\rceil .$$

The $n$-book graph $(n⩾2)$ is defined as the Cartesian product $K_{1,n}\square P_2$. We call every $C_4$ in the book graph $B_n$, a page of $B_n$. The distinguishing index of Cartesian product of star $K_{1,n}$ with path $P_m$ for $m⩾2$ and $n⩾2$ is $D^{\prime }(K_{1,n}\square P_m)=\lceil \sqrt[2m-1]{n}\rceil$, unless $m=2$ and $n=r^3$ for some integer $r$. In the latter case $D^{\prime }(K_{1,n}\square P_2)=\sqrt[3]{n}+1$, [10]. Since $B_n=K_{1,n}\square P_2$, using this equality we obtain the distinguishing index of book graph $B_n$.

Theorem 2.8

The entries in Table 1 are correct.

Table 1. Table of results for χ, D′ and χ′_D

Proof

The chromatic index and the distinguishing index for the classes of graphs given in this table are well-known, we justify the entries in the last column.

Paths of even order. The coloring that uses label 2 for one end-edge and label $1$ for the remaining edges is distinguishing, however, it is not a proper coloring and any proper coloring using two labels is not distinguishing, so ${\chi }_D^{\prime }\left(P_{2n}\right)\ge 3$. A $3$-coloring that is proper and distinguishing is achieved by using $1$ for an end-edge and alternating 2’s and 3’s for the remaining edges, thus ${\chi }_D^{\prime }\left(P_{2n}\right)\le 3$. Thus the result follows.

Cycles of even order $2n$, where $n\ge 4$. Let the consecutive edges of $C_{2n}$ be $e_1,e_2,\dots ,e_{2n}$. Using label 3 for edges $e_1$ and $e_4$, label 2 for edges $e_i$ where $i\ne 1$ is odd and label 1 for edges $e_i$ where $i\ne 4$ is even, we get ${\chi }_D^{\prime }\left(C_{2n}\right)\le 3$ for $n\ge 4$. All proper 2-colorings of edges of $C_{2n}$ have label preserving automorphisms, thus ${\chi }_D^{\prime }\left(C_{2n}\right)>2$ for all $n$. Therefore ${\chi }_D^{\prime }\left(C_{2n}\right)=3$, where $n\ge 4$.

Friendship and book graphs. It is clear that each proper $2n$-coloring of edges of $F_n$ is distinguishing and so ${\chi }_D^{\prime }\left(F_n\right)=2n$, by Theorem 2.2. For the book graph $B_n$, we present a proper $(n+1)$-distinguishing edge coloring. Let $v_0$ and $w_0$ be two vertices of degree $n+1$ of $B_n$, and $v_1,\dots ,v_n$ be the adjacent vertices to $v_0$, and $w_1,\dots ,w_n$ be the adjacent vertices to $w_0$, such that $v_0{v}_i{w}_i{w}_0$ for $1\le i\le n$ are pages of $B_n$. We label the edges $v_0{v}_i$, $v_i{w}_i$ and $w_i{w}_0$ with labels $i$, $i+2$ and $i+1$ mod $n$, respectively, for any $i$, $1\le i\le n$. Also, we label the edge $v_0{w}_0$ with label $n+1$. It can be seen that our coloring is a proper $(n+1)$-distinguishing coloring.

Complete graphs of even order. It is known that we can partition the edge set of $K_{2n}$ to $2n-1$ sets, each set contains an $n$-element perfect matching, say $M_1,\dots ,M_{2n-1}$. If we label the edges of $n$-element perfect matching $M_i$ with label $i$, for any $1\le i\le 2n-1$, then it can be seen that this coloring is proper. We claim that this coloring is distinguishing. If $f$ is an automorphism of $K_{2n}$ preserving the coloring, then $f$ fixes the set $M_i$, for any $1\le i\le 2n-1$, setwise. If $f$ is a nonidentity automorphism, then without loss of generality we can assume that $f\left(v_1\right)=v_2$. Since $f$ preserves the coloring so $f\left(v_2\right)=v_1$. We can suppose that there exists a vertex $x$ of $K_{2n}$ such that the edges $\{v_1,x\}$ and $\{v_2,f\left(x\right)\}$ are not in the same perfect matching. Thus the labels of edges $\{v_1,x\}$ and $\{v_2,f\left(x\right)\}$ are different, while $f$ maps these two edges to each other, which is a contradiction. Then, the identity automorphism is the only automorphism of $K_{2n}$ preserving the coloring, and hence the proper edge coloring is distinguishing, and so ${\chi }_D^{\prime }\left(K_{2n}\right)=2n-1$.

Complete bipartite graph $K_{n,n}$, $n\ge 4$. We can partition the edge set of $K_{n,n}$ to $n$ perfect matching $M_1,\dots ,M_n$, each of $M_i$ contains $n$ edges. For every value of $n$, the coloring that uses label $i$ for all edges in $M_i$, $1\le i\le n$, is a proper coloring. Also, every proper coloring of $K_{n,n}$ partitions the edges of $K_{n,n}$ to $n$ sets $N_1,\dots ,N_n$ such that each of $N_i$ is a perfect matching of $K_{n,n}$ and all edges in $N_i$ have the same label, and different from the label of edges in $N_j$ for every $i,j\in \{1,\dots ,n\}$ where $i\ne j$. However, for every proper coloring of $K_{n,n}$ we can find a nonidentity automorphism of $K_{n,n}$ preserving the coloring, thus ${\chi }_D^{\prime }\left(K_{n,n}\right)>n$. Now the result follows from Theorem 1.4.□

In sequel, we want to obtain a relationship between the chromatic distinguishing number of line graph $L\left(G\right)$ of graph $G$ and the chromatic distinguishing index of $G$. For this purpose, we need more information about automorphism group of $L\left(G\right)$. For a simple graph $G$, we recall that the line graph $L\left(G\right)$ is a graph whose vertices are edges of $G$ and where two edges $e,e^{\prime }\in V\left(L\left(G\right)\right)=E\left(G\right)$ are adjacent if they share an endpoint in common. Let ${\gamma }_G:\mathrm{Aut}\left(G\right)\to \mathrm{Aut}\left(L\left(G\right)\right)$ be given by $\left({\gamma }_G\varphi \right)\left(\{u,v\}\right)=\{\varphi \left(u\right),\varphi \left(v\right)\}$ for every $\{u,v\}\in E\left(G\right)$. In [11], Sabidussi proved the following theorem which we will use throughout.

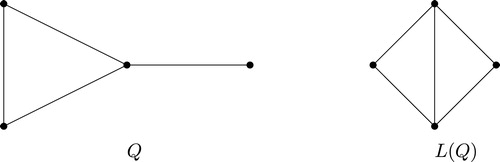
Theorem 2.9

[11] Suppose that $G$ is a connected graph that is not $P_2,Q$, or $L\left(Q\right)$ (see Fig. 1). Then $G$ is a group isomorphism, and so $\mathrm{Aut}\left(G\right)\cong \mathrm{Aut}\left(L\left(G\right)\right)$.

Fig. 1 Graphs $Q$ and $L\left(Q\right)$ of Fig. 1.

Theorem 2.10

Suppose that $G$ is a connected graph of order $n\ge 3$ that is not $Q$ and $L\left(Q\right)$. Then ${\chi }_D\left(L\left(G\right)\right)={\chi }_D^{\prime }\left(G\right)$.

Proof

First, we show that ${\chi }_D\left(L\left(G\right)\right)\le {\chi }_D^{\prime }\left(G\right)$. For this purpose, let $c:E\left(G\right)\to \{1,\dots ,{\chi }_D^{\prime }\left(G\right)\}$ be an edge proper distinguishing coloring of $G$. We define $c^{\prime }:V\left(L\left(G\right)\right)\to \{1,\dots ,{\chi }_D^{\prime }\left(G\right)\}$ such that $c^{\prime }\left(e\right)=c\left(e\right)$ where $e\in V\left(L\left(G\right)\right)=E\left(G\right)$. By the following steps we show that the vertex coloring $c^{\prime }$ is proper distinguishing coloring.

Step (1)

The vertex coloring $c^{\prime }$ is proper. If $e$ and $e^{\prime }$ are two adjacent vertices of $L\left(G\right)$ with $c^{\prime }\left(e\right)=c^{\prime }\left(e^{\prime }\right)$, then it means that $e$ and $e^{\prime }$ are incident edges of $G$ with $c\left(e\right)=c\left(e^{\prime }\right)$, which is impossible. Thus $c^{\prime }$ is a proper coloring.

Step (2)

The vertex coloring $c^{\prime }$ is a distinguishing vertex coloring of $L\left(G\right)$, because if $f$ is an automorphism of $L\left(G\right)$ preserving the coloring, then $c^{\prime }\left(f\left(e\right)\right)=c^{\prime }\left(e\right)$, and hence $c\left(f\left(e\right)\right)=c\left(e\right)$ for any $e\in E\left(G\right)$. On the other hand $f={\gamma }_G\varphi$ for some automorphism $\varphi$ of $G$, by Theorem 2.9. Thus from $c\left(f\left(e\right)\right)=c\left(e\right)$ for any $e\in E\left(G\right)$, we can conclude that $c\left({\gamma }_G\varphi \left(e\right)\right)=c\left(e\right)$ and so $c\left(\{\varphi \left(u\right),\varphi \left(v\right)\}\right)=c\left(\{u,v\}\right)$ for every $\{u,v\}\in E\left(G\right)$. This means that $\varphi$ is an automorphism of $G$ preserving the coloring $c$, so $\varphi$ is the identity automorphism of $G$. Therefore $f$ is the identity automorphism of $L\left(G\right)$, and hence ${\chi }_D\left(L\left(G\right)\right)\le {\chi }_D^{\prime }\left(G\right)$.

By a similar argument we can prove that ${\chi }_D\left(L\left(G\right)\right)\ge {\chi }_D^{\prime }\left(G\right)$, and so the result follows.□

Now we state a difference between the distinguishing coloring and chromatic distinguishing coloring of graphs.

Remark 2.11

Despite the distinguishing coloring that $D^{\prime }\left(G\right)\le D\left(G\right)+1$ for all connected graph $G$, it may be happened that ${\chi }_D^{\prime }\left(G\right)>{\chi }_D\left(G\right)+1$. For instance, let $G_n$ be the graph obtained from $K_{1,n}$ by replacing each edge with a path of length three. It can be computed that ${\chi }_D^{\prime }\left(G_8\right)=8$, while ${\chi }_D\left(G_8\right)=3$, see Fig. 2.

Fig. 2 A $3$-proper distinguishing vertex coloring of $G_8$.

We end this section by proposing the following problem.

Problem 2.12

Characterize all connected graphs with ${\chi }_D^{\prime }\left(G\right)={\chi }^{\prime }\left(G\right)=\Delta \left(G\right)$.

3 Results for join and corona products

In this section we study the distinguishing chromatic index of join and corona product of graphs. We start with join of graphs. The graph $G=(V,E)$ is the join of two graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$, if $V=V_1\cup V_2$ and $E=E_1\cup E_2\cup \left\{uv\right|u\in V_1,v\in V_2\}$ and denoted by $G=G_1+G_2$.

Theorem 3.1

If $G$ and$H$ are two connected graphs of orders $n,m\ge 3$, respectively, then $$max\{\Delta \left(H\right)+n,\Delta \left(G\right)+m\}\le \underset{D}{\overset{\prime }{\chi }}(G+H)\le max\{\underset{D}{\overset{\prime }{\chi }}\left(G\right),{\chi }_D^{\prime }\left(H\right)\}+{\chi }_D^{\prime }\left(K_{n,m}\right).$$

Proof

To prove the left inequality, it is sufficient to know that $\Delta (G+H)=max\{\Delta \left(H\right)+n,\Delta \left(G\right)+m\}$ and ${\chi }_D^{\prime }(G+H)\ge \Delta (G+H)$. For the right inequality, we first set $M≔max\{{\chi }_D^{\prime }\left(G\right),{\chi }_D^{\prime }\left(H\right)\}$. We label the edge set of graph $G$ (resp. $H$) with labels $\{1,\dots ,{\chi }_D^{\prime }\left(G\right)\}$ (resp. $\{1,\dots ,{\chi }_D^{\prime }\left(H\right)\}$) in a proper distinguishing way. If $V\left(G\right)=\{v_1,\dots ,v_n\}$ and $V\left(H\right)=\{w_1,\dots ,w_m\}$, then we label the middle edges $\{v_i{w}_j:1\le i\le n,1\le j\le m\}$, exactly the same as a proper distinguishing coloring of the complete bipartite graph $K_{\left|V\left(G\right)\right|,\left|V\left(H\right)\right|}$ with labels $\{M+1,\dots ,M+{\chi }_D^{\prime }\left(K_{\left|V\left(G\right)\right|,\left|V\left(H\right)\right|}\right)\}$. Since the graphs $G$ and $H$ have a proper coloring, so this coloring of edges of $G+H$ is proper, regarding to the label of middle edges. To show this coloring is distinguishing, we suppose that $f$ is an automorphism of $G+H$ preserving the coloring. Then, with respect to the label of middle edges, it can be concluded that the restriction of $f$ to the vertices of $G$ (resp. $H$) is an automorphism of $G$ (resp. $H$) preserving the coloring. Since the graphs $G$ and $H$ have been labeled distinguishingly, so the restriction of $f$ to vertices of $G$ and $H$ is the identity automorphism of $G$ and $H$, respectively. Therefore, this coloring is distinguishing. □

The lower and upper bounds of Theorem 3.1 are sharp. For example, we consider $P_{2n+1}+P_{2m+1}$ where $m>n$, with ${\chi }_D^{\prime }(P_{2n+1}+P_{2m+1})=2m+3$. In fact, we can label the edge set of $P_{2n+1}$ and $P_{2m+1}$ with labels 1 and 2 in a proper distinguishing way, and label the remaining incident edges to each vertex of $P_{2n+1}$ with distinct labels $3,4,\dots ,2m+3$ such that the incident edges to each vertex of $P_{2m+1}$ in $P_{2n+1}+P_{2m+1}$ have distinct labels.

Now we want to obtain a lower and anupper bound for the distinguishing chromatic index of corona product. The corona product $G\circ H$ of two graphs $G$ and $H$ is defined as the graph obtained by taking one copy of $G$ and $\left|V\left(G\right)\right|$ copies of $H$ and joining the $i$th vertex of $G$ to every vertex in the $i$th copy of $H$. If $G$ and $H$ be two connected graphs such that $G\ne K_1$, then there is no vertex in the copies of $H$ which has the same degree as a vertex in $G$. Because if there exist a vertex $w$ in one of the copies of $H$ and a vertex $v$ in $G$ such that ${deg}_{G\circ H}\left(v\right)={deg}_{G\circ H}\left(w\right)$, then ${deg}_G\left(v\right)+\left|V\left(H\right)\right|={deg}_H\left(w\right)+1$. So we have ${deg}_H\left(w\right)+1>\left|V\left(H\right)\right|$, which is a contradiction. Hence, we can state the following lemma.

Lemma 3.2

Let $G$ and$H$ be two connected graphs such that $G\ne K_1$. If $f$ is an arbitrary automorphism of $G\circ H$, then the restriction of $f$ to the vertices of copy $G$ (resp. $H$) is an automorphism of $G$ (resp. $H$).

Theorem 3.3

If $G$ and$H$ are two connected graphs of orders $n,m\ge 3$, respectively, then $$max\{\Delta \left(G\right)+m,\Delta \left(H\right)+1\}\le \underset{D}{\overset{\prime }{\chi }}(G\circ H)\le max\{\underset{D}{\overset{\prime }{\chi }}\left(G\right),{\chi }_D^{\prime }\left(H\right)\}+m.$$

Proof

The proof of the left inequality is exactly the same as Theorem 3.1. To prove the right inequality, we first set $M≔max\{{\chi }_D^{\prime }\left(G\right),{\chi }_D^{\prime }\left(H\right)\}$. We label the edge set of graph $G$ (resp. $H$) with labels $\{1,\dots ,{\chi }_D^{\prime }\left(G\right)\}$ (resp. $\{1,\dots ,{\chi }_D^{\prime }\left(H\right)\}$) in a proper distinguishing way. If $V\left(G\right)=\{v_1,\dots ,v_n\}$ and $V\left(H\right)=\{w_1,\dots ,w_m\}$, then we label the middle edge $v_i{w}_j$ with label $M+j$ for any $1\le i\le n$ and $1\le j\le m$. Since the graphs $G$ and $H$ have been labeled properly, so this coloring of edges of $G\circ H$ is proper, due to the label of middle edges. To show this coloring is distinguishing, we suppose that $f$ is an automorphism of $G\circ H$ preserving the coloring. Then, by Lemma 3.2, it can be concluded that the restriction of $f$ to the vertices of $G$ (resp. $H$) is an automorphism of $G$ (resp. $H$) preserving the coloring. Since the graphs $G$ and $H$ have been labeled distinguishingly, so the restriction of $f$ to vertices of $G$ and $H$ is the identity automorphism of $G$ and $H$ respectively. Therefore, this coloring is distinguishing. □

The lower and upper bounds of Theorem 3.3 are sharp. For instance, we consider $K_{2n}\circ K_{2m+1}$ where $3\le m<n$. It can be easily computed that ${\chi }_D^{\prime }(K_{2n}\circ K_{2m+1})=2m+2n$. Now, since $max\{\Delta \left(K_{2n}\right)+2m+1,\Delta \left(K_{2m+1}\right)+1\}=2m+2n$ and $max\{{\chi }_D^{\prime }\left(K_{2n}\right),{\chi }_D^{\prime }\left(K_{2m+1}\right)\}+2m+1=2m+2n$, so the bounds of Theorem 3.3 are sharp.

We end this paper by a remark on the distinguishing chromatic index of join and corona product of graphs $G$ and $H$ where $G=K_1$ or $K_2$.

Remark 3.4

(i)	If $G$ and $H$ are two connected graphs such that $G=K_1$ or $K_2$, then the maximum degree of $G+H$ is $\left|V\left(H\right)\right|$ or $\left|V\left(H\right)\right|+1$, respectively, and so ${\chi }_D^{\prime }(G+H)\le \left|V\left(H\right)\right|+2$, except for $G=H=K_2$. In the latter case, ${\chi }_D^{\prime }(K_2+K_2)=5$.
(ii)	It is clear that $K_1\circ H=K_1+H$, and so ${\chi }_D^{\prime }(K_1\circ H)={\chi }_D^{\prime }(K_1+H)$. If $G=K_2$, then $\Delta (K_2\circ H)=\left|V\left(H\right)\right|+1$, and so ${\chi }_D^{\prime }(K_2\circ H)\le \left|V\left(H\right)\right|+2$.