Betweenness centrality in Cartesian product of graphs

Abstract

Betweenness centrality is a widely used measure in various graphs and it has a pivotal role in the analysis of complex networks. It measures the potential or power of a node to control the communication over the network. The computation is based on the assumption that information primarily flows over the shortest paths between the nodes of the network. In a graph, the power of a vertex is not an individual attribute, it depends on the influence of other vertices present. Betweenness centrality measures the extent to which a vertex becomes part of the shortest paths between pairs of other vertices in a graph. In this paper, we establish expression for betweenness centrality in Cartesian product of graphs. And investigate the same on certain graphs such as grid, Hamming graphs, hypercubes, Cartesian product of cycles etc.

Keywords:

• Betweenness centrality
• Pairwise dependency
• Cartesian product
• Geodetic graph

1 Introduction

Several centrality measures have so far been studied and their importance is increasing day by day. Betweenness centrality has a vital role in the analysis of networks. [1–4] It has many applications in a variety of domains such as biological networks [5–9], study of sexual networks and AIDS [10], identifying key actors in terrorist networks [11], transportation networks [12], supply chain management [13], bio-informatics–protein interaction networks [14,15], food webs [16] etc. Betweenness centrality [17,18] indicates the betweenness of a vertex (or an edge) in a network and it measures the extent to which a vertex (or an edge) lies on the shortest paths between pairs of other vertices. It is quite difficult to find out the betweenness centrality of a vertex in a large graph. The computation of this index based on direct application of definition becomes impractical when the number of vertices $n$ is huge since it has complexity in the order of $\mathcal{O}\left(n^3\right)$. The fastest exact algorithm due to Brandes [19] requires $\mathcal{O}(n+m)$ space and $\mathcal{O}\left(nm\right)$ time where $n$ is the number of vertices and $m$ the number of edges in the graph. Exact computations of betweenness centrality can take a lot of time. But a large network can be thought of as it is made by joining smaller networks together. There are several graph operations which results in a larger graph and hence many of the properties of larger graphs can be derived from its constituent subgraphs. Graph operations are helpful for constructing new classes of composite graphs. Cartesian product is an important graph operation.

It is assumed that the graphs under consideration are simple undirected connected graphs.

2 Background

The concept of betweenness centrality of a vertex was first introduced by Bavelas in 1948 [20]. The importance of the concept of vertex centrality lies on how a vertex acts as a bridge among pairs of vertices in joining them by shortest paths. It gives the potential of a vertex for control of information flow in the network [21,22]. The following terminology is used. The order of a graph $G$, denoted by $\left|G\right|$, is the number of vertices in $G$. i.e., $\left|G\right|=\left|V\left(G\right)\right|$. The distance between two vertices $u,v\in V\left(G\right)$, denoted by $d_G(u,v)$, is the length of any shortest $u$-$v$ path in $G$. A shortest $u$-$v$ path is also called a u-v geodesic. A graph $G$ is a geodetic graph [23] if every pair of vertices of $G$ is connected by a unique shortest path. The diameter, $diam\left(G\right)$, of a graph $G$ is given by $max\left\{d(u,v)\right|u,v\in V\left(G\right)\}$. Two vertices $u$ and $v$ of $G$ satisfying $d(u,v)=diam\left(G\right)$ are extreme vertices [24]. For a connected graph $G$ and $u,v\in G$, the interval $I_G(u,v)$ between $u$ and $v$ is defined as the set of vertices that lie on shortest $u$-$v$ paths; that is, $$I_G(u,v)=\{w\in G:d(u,v)=d(u,w)+d(w,v)\}$$

A graph $G$ is vertex-transitive if every vertex in $G$ can be mapped to any other vertex by some automorphism. A subgraph $U$ of a graph $G$ is isometric in $G$ if $d_U(u,v)=d_G(u,v)$ for all $u,v\in U$. A subgraph $U$ of a graph $G$ is (geodesically)convex in $G$ if $U$ contains all $u$-$v$ geodesics of $G$ for $u,v\in U$.

A definition to betweenness centrality of a vertex in a graph $G$, given by Freeman [25] is as follows

Definition 2.1

Betweenness Centrality If $x\in V\left(G\right)$, the betweenness centrality $B\left(x\right)$ for $x$ is defined as $$B\left(x\right)=\sum _{\genfrac{}{}{0ex}{}{\{u,v\}\subseteq V\left(G\right)}{u\ne v\ne x}}\delta (u,v|x)$$where $\delta (u,v|x)$ is called the pair-dependency of the pair $\{u,v\}$ on $x$. It is defined as $\delta (u,v|x)=\frac{\sigma (u,v|x)}{\sigma (u,v)}$ where $\sigma (u,v)$ is the number of shortest $u$-$v$ paths and $\sigma (u,v|x)$ is the number of shortest $u$-$v$ paths containing $x$.

Observe that $x\in V\left(G\right)$ lies on the shortest $u$-$v$ path iff $d(u,v)=d(u,x)+d(x,v)$. The number of shortest $u$-$v$ paths passing through $x$ is given by $$\sigma (u,v|x)=\sigma (u,x)\times \sigma (x,v)$$

Definition 2.2

Cartesian Product, [26] The Cartesian product of two graphs $G$ and $H$, denoted by $G\square H$, is a graph with vertex set $V\left(G\right)\times V\left(H\right)$, where two vertices $(g,h)$ and $(g^{\prime },h^{\prime })$ are adjacent if $g=g^{\prime }$ and $h{h}^{\prime }\in E\left(H\right)$, or $g{g}^{\prime }\in E\left(G\right)$ and $h=h^{\prime }$. The graphs $G$ and $H$ are called factors of the product $G\square H$.

For any $h\in V\left(H\right)$, the subgraph of $G\square H$ induced by $V\left(G\right)\times \left\{h\right\}$ is called $G$-fiber or $G$-layer, denoted by $G^h$. Similarly, we can define $H$-fiber or $H$-layer. They are isomorphic to $G$ and $H$ respectively. $G\square H$ contains $\left|H\right|$ copies of $G$ and $\left|G\right|$ copies of $H$. Projections are the maps from a product graph to its factors. They are weak homomorphisms in the sense that they respect adjacency. The two projections on $G\square H$ namely $p_G:G\square H\to G$ and $p_H:G\square H\to H$ defined by $p_G(g,h)=g$ and $p_H(g,h)=h$ refer to the corresponding $G$-, $H$- coordinates. Thus an edge in $G\square H$ is mapped into a single vertex by one of the projections $p_G$ or $p_H$ and mapped into an edge by the other. If $G$ and $H$ are connected, then $G\square H$ is also connected. Furthermore, the minimum degree denoted by $\delta \left(G\right)$ is additive under Cartesian products, i.e. $\delta (G\square H)=\delta \left(G\right)+\delta \left(H\right)$. Assuming isomorphic graphs are equal, Cartesian product is commutative as well as associative.

Lemma 2.1

[27] Let $G$ and$H$ be connected graphs. Then all $G$-fibers and$H$-fibers are convex subgraphs of $G\square H$.

Definition 2.3

Cartesian Product of Several Graphs, [27] The Cartesian product $G={\square }_{i=1}^k{G}_i$ of graphs $G_1,G_2,\dots ,G_k$ is defined on the $k$-tuples $(v_1,v_2,\dots ,v_k)$, where $v_i\in G_i,1\le i\le k$ in such a way that two $k$-tuples $(u_1,u_2,\dots ,u_k)$ and $(v_1,v_2,\dots ,v_k)$ are adjacent if there exists an index $l$ such that $[u_l,v_l]\in E\left(G_l\right)$ and $u_i=v_i$ for $i\ne l$. The $k$-tuple $(v_1,v_2,\dots ,v_k)$ is called coordinate vector, and the $v_i$ are the coordinates.

The Cartesian product $G=G_1\square G_2\square \dots \square G_k$ of $k$-factors is briefly denoted as $G={\square }_{i=1}^k{G}_i$. The $n$th Cartesian product of a graph $G$ is denoted as $G^n={\square }_{i=1}^{n}G$. It is to be noted that the product $G$ is connected if and only if each of its factor $G_i$ is connected and the diameter of the product is given by, $diam\left({\square }_{i=1}^k{G}_i\right)={\sum }_{i=1}^{k}diam\left(G_i\right)$.

Proposition 2.1

[28] The Cartesian product $G={\square }_{i=1}^k{G}_i$ is vertex-transitive, if $G_i$ is vertex-transitive for each $i=1,2,\dots ,n$

The following proposition shows that the distance between two vertices in the product graph is the sum of the distance between their projections in the factor graphs.

Lemma 2.2

[29] If $(g,h)$ and$(g^{\prime },h^{\prime })$ are vertices of a Cartesian product $G\square H$, then (1) $$d_{G\square H}\left[(g,h),(g^{\prime },h^{\prime })\right]=d_G(g,g^{\prime })+d_H(h,h^{\prime })$$(1)

This can be generalized to the following lemma.

Lemma 2.3

Distance Lemma [29] Let $G$ be the Cartesian product $G={\square }_{i=1}^k{G}_i$ of connected graphs, and let $g=(g_1,\dots ,g_k)$ and $g^{\prime }=(g_1^{\prime },\dots ,g_k^{\prime })$ be vertices of $G$. Then $$d_G(g,g^{\prime })=\sum _{i=1}^k{d}_{G_i}(g_i,g_i^{\prime })$$

Lemma 2.2 implies that $d_{G\square H}\left[(g,h),(g^{\prime },h)\right]=d_{G^h}(g,h),(g^{\prime },h)$. In other words, $d_{G\square H}$ restricted to $G^h$ is $d_{G^h}$. It means that every shortest path in a $G$-fiber (or $H$-fiber) ia also a shortest path in $G\square H$. Consider the following betweenness property of vertices in product graph.

Proposition 2.2

[27] Let $v_1=(g_1,h_1)$ and$v_2=(g_2,h_2)$ be two vertices of $G\square H$, then the vertex $v_3=(g_3,h_3)$ lies in $I_{G\square H}(v_1,v_2)$ if and only if $g_3\in I_G(g_1,g_2)$ and $h_3\in I_H(h_1,h_2)$.

It can be generalized as the following

Proposition 2.3

[27] Let $G={\square }_{i=1}^k{G}_{{}_i}$. Let $g(g_1,g_2,\dots ,g_k)$,$g^{\prime }(g_1^{\prime },g_2^{\prime },\dots ,g_k^{\prime })$ and$g^{\prime \prime }(g_1^{\prime \prime },g_2^{\prime \prime },\dots ,g_k^{\prime \prime })$ be any three vertices in $G$. Then $g^{\prime \prime }\in I_G(g,g^{\prime })$ if and only if $g_i^{\prime \prime }\in I_{G_i}(g_i,g_i^{\prime })$ $\forall i$.

3 The betweenness centrality of vertices in Cartesian product of graphs

The following proposition shows how the number of geodesics between two vertices $u$ and $v$ in a product graph $G\square H$ is related to the number of geodesics between their projections in the factor graphs.

Proposition 3.1

If $u=(g,h)$ and$v=(g^{\prime },h^{\prime })$ are vertices in$G\square H$, then the number of shortest$u$-$v$ paths in $G\square H$ is given by (2) $${\sigma }_{G\square H}\left[(g,h),(g^{\prime },h^{\prime })\right]={\sigma }_G(g,g^{\prime })\times {\sigma }_H(h,h^{\prime })\times \left(\genfrac{}{}{0ex}{}{d_G(g,g^{\prime })+d_H(h,h^{\prime })}{d_G(g,g^{\prime })}\right)$$(2)

Proof

Consider the vertices $u=(g,h)$ and $v=(g^{\prime },h^{\prime })$ in $G\square H$. Let $d=d(u,v)$ denote the distance between $u$ and $v$ in $G\square H$. Suppose there exist unique shortest paths between $g$ and $g^{\prime }$ in $G$ and $h$ and $h^{\prime }$ in $H$. A shortest path from $u$ to $v$ is a sequence of $d$ edges and the image of each edge under the projections $p_G$ and $p_H$ is an edge lying between $g$ and $g^{\prime }$ or $h$ and $h^{\prime }$. If the sequence of $d$ edges of the $u$-$v$ path in $G\square H$ makes a sequence of $d_G$ edges in $G$ and a sequence of $d_H$ edges in $H$, then $d=d_G+d_H$. Since $d_G$ and $d_H$ are the same for any shortest $u$-$v$ path, the number of shortest paths between $u$ and $v$ in $G\square H$ is the number of ways of selecting $d_G$ edges (or $d_H$ edges) from $d$ edges which is $\left(\genfrac{}{}{0ex}{}{d}{d_G}\right)$. If there exist ${\sigma }_G$ shortest paths between $g$ and $g^{\prime }$ in $G$ and ${\sigma }_H$ shortest paths between $h$ and $h^{\prime }$ in $H$, then corresponding to each pair, there exist $\left(\genfrac{}{}{0ex}{}{d}{d_G}\right)$ shortest paths between $u$ and $v$ in $G\square H$.

Therefore, ${\sigma }_{G\square H}\left[(g,h),(g^{\prime },h^{\prime })\right]={\sigma }_G(g,g^{\prime })\times {\sigma }_H(h,h^{\prime })\times \left(\genfrac{}{}{0ex}{}{d_G(g,g^{\prime })+d_H(h,h^{\prime })}{d_G(g,g^{\prime })}\right)$

For brevity, we may write ${\sigma }_{G\square H}={\sigma }_G\times {\sigma }_H\times \left(\genfrac{}{}{0ex}{}{d_{G\square H}}{d_G}\right)$ □

Corollary 3.1

If $G$ and$H$ are geodetic graphs, then the number of shortest paths between$(g,h)$ and$(g^{\prime },h^{\prime })$ in$G\square H$ is given by $${\sigma }_{G\square H}\left[(g,h),(g^{\prime },h^{\prime })\right]=\left(\genfrac{}{}{0ex}{}{d_G(g,g^{\prime })+d_H(h,h^{\prime })}{d_G(g,g^{\prime })}\right)$$

By the associativity of $\square$, Eq. (2) can be generalized as

Proposition 3.2

Let $G={\square }_{i=1}^k{G}_{n_i}$. If $u=(u_1,u_2,\dots ,u_k)$,$v=(v_1,v_2,\dots ,v_k)$ are two vertices in $G$ such that ${\sigma }_{G_i}(u_i,v_i)={\sigma }_i$,$d_{G_i}(u_i,v_i)=d_i$ and$d=\sum d_i$, then $${\sigma }_G(u,v)={\sigma }_1{\sigma }_2\dots {\sigma }_n\left(\genfrac{}{}{0ex}{}{d}{d_1}\right)\left(\genfrac{}{}{0ex}{}{d-d_1}{d_2}\right)\left(\genfrac{}{}{0ex}{}{d-d_1-d_2}{d_3}\right)\dots 1$$

Corollary 3.2

Let $G={\square }_{i=1}^k{G}_{n_i}$ where each $G_{n_i}$ are geodetic. If $u=(u_1,u_2,\dots ,u_k)$,$v=(v_1,v_2,\dots ,v_k)$ are two vertices in $G$ such that $d_{G_i}(u_i,v_i)=d_i$ and $d=\sum d_i$, then

$${\sigma }_G(u,v)=\left(\genfrac{}{}{0ex}{}{d}{d_1}\right)\left(\genfrac{}{}{0ex}{}{d-d_1}{d_2}\right)\left(\genfrac{}{}{0ex}{}{d-d_1-d_2}{d_3}\right)\dots 1$$

Proposition 3.3

Let $v_1$,$v_2$ and$v_3$ be any three vertices in $G\square H$. Then (3) $${\sigma }_{G\square H}(v_1,v_2|v_3)={\sigma }_{G\square H}(v_1,v_3)\times {\sigma }_{G\square H}(v_3,v_2)$$(3)

Theorem 3.1

The betweenness centrality of $x=(g_0,h_0)$ in $G\square H$ is given by $$B_{G\square H}\left(x\right)=\sum _{\genfrac{}{}{0ex}{}{u\ne v\ne x}{\{u,v\}\subseteq V(G\square H)}}{\delta }_{G\square H}(u,v|x)$$where $${\delta }_{G\square H}(u,v|x)={\delta }_G(g,g^{\prime }|g_0)\times {\delta }_H(h,h^{\prime }|h_0)\times \frac{D_1\times D_2}{D}$$with $$D_1=\left(\genfrac{}{}{0ex}{}{d_G(g,g_0)+d_H(h,h_0)}{d_G(g,g_0)}\right),D_2=\left(\genfrac{}{}{0ex}{}{d_G(g_0,g^{\prime })+d_H(h_0,h^{\prime })}{d_G(g_0,g^{\prime })}\right),D=\left(\genfrac{}{}{0ex}{}{d_G(g,g^{\prime })+d_H(h,h^{\prime })}{d_G(g,g^{\prime })}\right)$$

Proof

The result follows from the definition of betweenness centrality and from Eqs. (1)–(3)

Hence $${\delta }_{G\square H}(u,v|x)=\frac{{\sigma }_{G\square H}(u,v|x)}{{\sigma }_{G\square H}(u,v)}=\frac{{\sigma }_G(g,g^{\prime }|g_0)}{{\sigma }_G(g,g^{\prime })}\times \frac{{\sigma }_H(h,h^{\prime }|h_0)}{{\sigma }_H(h,h^{\prime })}\times \frac{D_1\times D_2}{D}\square$$

Definition 3.1

Wiener Index of a Graph, [30] The Wiener index of a graph $G$, denoted by $W\left(G\right)$ is the sum of the distances between all (unordered) pairs of vertices of $G$. i.e., $$W\left(G\right)=\sum _{i<j}d(v_i,v_j)$$or, $$W\left(G\right)=\frac{1}{2}\sum _{u,v\in V\left(G\right)}d(u,v)$$

Wiener index is also named total status or total distance of a graph. The Wiener index of Cartesian product [31–33] of two graphs $G$ and $H$ is given by $$W(G\square H)={\left|G\right|}^{2}W\left(H\right)+{\left|H\right|}^{2}W\left(G\right)$$It can be extended to (4) $$W\left({\square }_{i=1}^n{G}_i\right)=\sum _{i=1}^n\left(W\left(G_i\right)\prod _{j\ne i}{\left|G_j\right|}^2\right)$$(4) The betweenness centrality of $G$ is given by $$\sum _{v\in V\left(G\right)}B\left(v\right)=W\left(G\right)-\left(\genfrac{}{}{0ex}{}{\left|G\right|}{2}\right)$$If $G$ is vertex transitive, the betweenness centrality of $v\in G$ is given by (5) $$B\left(v\right)=\frac{W\left(G\right)-\left(\genfrac{}{}{0ex}{}{\left|G\right|}{2}\right)}{\left|G\right|}$$(5)

3.1 Grid graphs

Grid graphs are the Cartesian product of path graphs. $P_m\square P_n$ represents a rectangular grid $R$. If $u=(g,h)$ and $v=(g^{\prime },h^{\prime })$ are any two vertices of $R$, then $d(u,v)=|g-g^{\prime }|+|h-h^{\prime }|$ ($l^1$-metric) and $\sigma (u,v)=\left(\genfrac{}{}{0ex}{}{d}{d_1}\right)$ where $d_1=|g-g^{\prime }|$ or $|h-h^{\prime }|$.

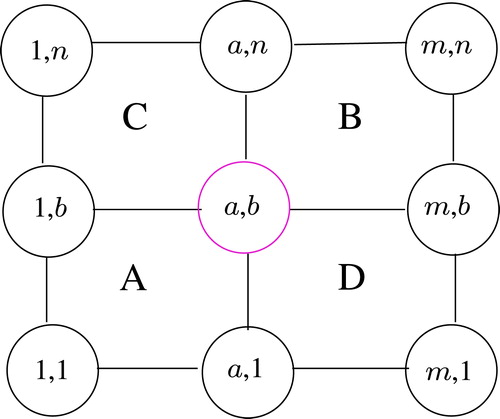
Consider the rectangular grid $P_m\square P_n$ given in Fig. 3.1. Take a vertex $x$ in $P_m\square P_n$; then $x=(a,b)$, where $1\le a\le m,1\le b\le n$. The paths $P_n^a$ and $P_m^b$ passing through $(a,b)$ divide the rectangular grid into four quadrants $A,B,C,D$ sharing their common sides. Any pair of vertices lying in the diagonal regions $A,B$ or $C,D$ makes a contribution to the betweenness centrality of $(a,b)$. Hence

Fig. 3.1. Rectangular grid P_m□P_n.

$$B\left[(a,b)\right]=\sum _{u,v}\frac{\sigma (u,x)\sigma (x,v)}{\sigma (u,v)}+\sum _{w,z}\frac{\sigma (w,x)\sigma (x,z)}{\sigma (w,z)}-\left[(a-1)\times (m-a)+(b-1)\times (n-b)\right]$$where $u\in A$, $v\in B,w\in C$ and $z\in D$ .

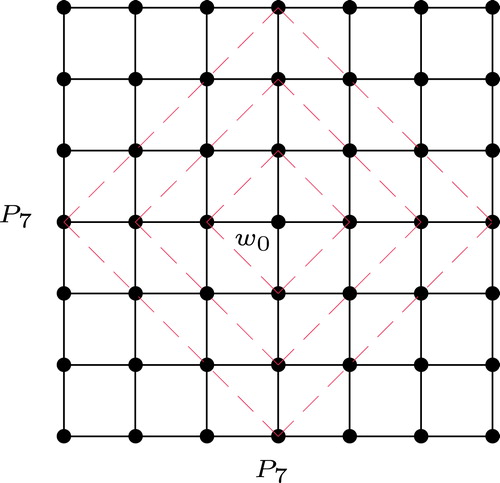
Lemma 3.1

In an $m\times n$ grid, for any inner vertex $w_0=(a,b)$, the vertices at a distance $d=min\{a,b,m-a,m-b\}>0$ from $w_0$ induces it the betweenness centrality $4d$

Proof

Consider the $k$-neighborhood ($k$-nbd) of $w_0$ where $k=min\{a,b,m-a,m-b\}>0$. Each $k$-nbd of $w_0$ contains $4d$ vertices at a distance $d$ from $w_0$ for $1\le d\le k$ and they are lying on a rhombus as in Fig. 3.2). Consider the vertices $u$ and $v$ lying on opposite sides of the rhombus where $d(u,w_0)=r_1+(d-r_1)$ and $d(v,w_0)=r_2+(d-r_2)$ for $0\le r_1,r_2\le d$ such that $d(u,v)=2d$. Now the pair $(u,v)$ induces the betweenness centrality $\frac{\left(\genfrac{}{}{0ex}{}{d}{r_1}\right)\left(\genfrac{}{}{0ex}{}{d}{r_2}\right)}{\left(\genfrac{}{}{0ex}{}{2d}{r_1+r_2}\right)}$ to $w_0$. Split the distance $d(u,v)=2d$ into $(2d-r)+r$, the horizontal and vertical components and consider the pairs of vertices $(u,v)$ for each $r$. It can be easily seen that they contribute the betweenness centrality 2 for $r=0$; 4 for $1\le r\le d-1$; 2 for $r=d$. Thus the betweenness centrality induced by the vertices at a distance $d$ is given by $2+4(d-1)+2=4d$.□

Fig. 3.2. Neighborhood of w₀ in P₇□P₇.

Theorem 3.2

In an $m\times n$ grid, for any vertex $w_0=(a,b),1<a<m,1<b<n$, the $k$-nbd of$w_0$ where$k=min\{a,b,m-a,m-b\}>0$ denoted by $N_k\left(w_0\right)$ contains$2k(k+1)$ vertices and the betweenness centrality of $w_0$ induced by $N_k\left(w_0\right)$ is given by $$B\left(w_0,N_k\left(w_0\right)\right)=2k^2(k+1)$$

Proof

Let $w_0$ be an inner vertex of the $m\times n$ grid. Then the pairs of vertices $(u,v)$ for $d(u,w_0)=r_1$ and $d(v,w_0)=r_2$ such that $d(u,v)=r_1+r_2=d$ induces a betweenness centrality $2d$. Since there exist $d-1$ pairs of $(r_1,r_2)$ for $d\ge 2$, the pairs of vertices at a distance $d$ induce a betweenness centrality $2d(d-1)$. To find the betweenness centrality of $w_0$ induced by $N_k\left(w_0\right)$, consider $(r_1,r_2)$ for $1\le r_1,r_2\le k$ and we get $$B\left(w_0,N_k\left(w_0\right)\right)=\sum _{d=2}^{k+1}2d(d-1)+\sum _{r=2}^{k}2(k+r)(k-r+1)=2k^2(k+1)\square$$

Remark 1

Using Corollary 3.2 the number of geodesics of length $kn$ in the grid $G={\square }_{i=1}^k{P}_{n+1}$ from $(0,0,\dots ,ktimes)$ to $(n,n,\dots ,ktimes)$ obtained follows the $k$-ary de Bruijn sequence $s(k,n)$ where $s(k,n)=\frac{\left(kn\right)!}{{(n!)}^k}$ ($OEIS$ $A000984$)

3.2 Hamming graphs

Hamming graphs are Cartesian products of complete graphs. i.e., $H={\square }_{i=1}^r{K}_{n_i}$ for some $r\ge 1$ and $n_i\ge 2$. The vertices of $H$ can be labeled with vector $(a_1,a_2,\dots ,a_r)$ where $a_i\in \{0,1,\dots ,n_i-1\}$. Two vertices of $H$ are adjacent if the corresponding vectors differ in precisely one coordinate. The distance (named Hamming distance) between two vertices $u$ and $v$ denoted by $d(u,v)$ is the number of positions in which the two vectors differ.

Hypercubes are Cartesian product of complete graphs $K_2$. An $r$-dimensional hypercube (or $r$-cube) denoted by $Q_r$ is given by, $Q_r={\square }_{i=1}^r{K}_2$. It can also be defined recursively, $Q_r=K_2\square Q_{r-1}$. Hypercubes are important classes of graphs having many interesting structural properties. The number of geodesics between $u,v\in Q_r$ is given by $\sigma (u,v)=d(u,v)!$. For a connected graph $G$, the condition “$I(u,v)$ induces a $d(u,v)$-dimensional hypercube for any two vertices $u$ and $v$ of $G$ ” implies that $G$ is a Hamming graph [24].

The following lemma highlights the importance of Hamming graphs.

Lemma 3.2

[34] A graph $G$ is a nontrivial subgraph of the Cartesian product of graphs if and only if$G$ is a nontrivial subgraph of the Cartesian product of two complete graphs.

Proposition 3.4

Let $H$ be the Hamming graph given by $H=K_{n_1}\square K_{n_2}\square \dots \square K_{n_r}$. Then the betweenness centrality of $v\in H$ is given by $$B\left(v\right)=\frac{1}{2}\prod _{i=1}^r{n}_i\left[r-1-\sum _{i=1}^r\frac{1}{n_i}\right]+\frac{1}{2}$$

Proof

Let $H={\square }_{i=1}^r{K}_{n_i}$. Since $H$ is vertex transitive, from Eqs. (4) and (5), $$W\left(H\right)=\sum _{i=1}^{r}W\left(K_{n_i}\right)\prod _{j=1,j\ne i}^r{\left|K_{n_j}\right|}^2=\sum _{i=1}^r\left(\genfrac{}{}{0ex}{}{n_i}{2}\right)\prod _{j=1,j\ne i}^r{n}_j^2=\frac{1}{2}{\left(\prod _{i=1}^r{n}_i\right)}^2\left[r-\sum _{i=1}^r\frac{1}{n_i}\right]$$$$B_H\left(v\right)=\frac{W\left(H\right)-\left(\genfrac{}{}{0ex}{}{\left|H\right|}{2}\right)}{\left|H\right|}=\frac{1}{2}\prod _{i=1}^r{n}_i\left[r-1-\sum _{i=1}^r\frac{1}{n_i}\right]+\frac{1}{2}\square$$

Corollary 3.3

If $K_p$,$K_q$ and$K_r$ are complete graphs, then for $v\in K_p\square K_q$ $$B\left(v\right)=\frac{(p-1)(q-1)}{2}$$for $v\in K_p\square K_q\square K_r$ $$B\left(v\right)=\frac{1}{2}\left[2pqr-(pq+pr+qr)+1\right]$$

Corollary 3.4

If $v\in {\square }_{i=1}^r{K}_n$, then $$B\left(v\right)=\frac{1}{2}\left[(r-1)n^r-r{n}^{r-1}+1\right]$$when $n=2$,$v\in {\mathrm{Q}}_{\mathrm{r}}$, the$r$-cube, then $$B\left(v\right)=(r-2)2^{r-2}+\frac{1}{2}$$

3.3 Product of cycles

Consider the product of cycles ${\square }_{i=1}^r{C}_{n_i}$. Now from Eqs. (4) we get for $n_i\in 2{\mathbb{Z}}^{+}$ (6) $$W\left({\square }_{i=1}^n{C}_{n_i}\right)=\frac{1}{8}{\left(\prod _{i=1}^r{n}_i\right)}^2\sum _{i=1}^r{n}_i$$(6) and for $n_i\in 2{\mathbb{Z}}^{+}+1$ (7) $$W\left({\square }_{i=1}^n{C}_{n_i}\right)==\frac{1}{8}{\left(\prod _{i=1}^r{n}_i\right)}^2\sum _{i=1}^r\left(n_i-\frac{1}{n_i}\right)$$(7) For any $C_n$, $W\left(C_n\right)=\frac{1}{8}{n}^3$ when $n$ is even, and $W\left(C_n\right)=\frac{1}{8}(n^3-n)$ when $n$ is odd. Now from Eqs. (5)–(7) we get

Proposition 3.5

If $G$ is the Cartesian product of $r$ even cycles. i.e., $G={\square }_{i=1}^r{C}_{n_i}$ , $n_i\in 2{\mathbb{Z}}^{+}$, then for $v\in G$ $$B\left(v\right)=\frac{1}{8}\left[\prod _{i=1}^r{n}_i\sum _{i=1}^r{n}_i-4\left(\prod _{i=1}^r{n}_i-1\right)\right]$$if $n_i=2k_i$, $$B\left(v\right)=2^{r-2}\prod _{i=1}^r{k}_i\left[\sum _{i=1}^r{k}_i-2\right]+\frac{1}{2}$$

Proposition 3.6

If $G$ is the Cartesian product of $r$ odd cycles. i.e., $G={\square }_{i=1}^r{C}_{n_i}$ , $n_i\in 2{\mathbb{Z}}^{+}+1$, then for $v\in G$ $$B\left(v\right)=\frac{1}{8}\left[\prod _{i=1}^r{n}_i\sum _{i=1}^r\left(n_i-\frac{1}{n_i}\right)-4\left(\prod _{i=1}^r{n}_i-1\right)\right]$$

Corollary 3.5

Consider two cycles $C_m$ and $C_n$. Let $v\in C_m\square C_n$ then $$B\left(v\right)=\left\{\begin{array}{c}\frac{1}{8}(mn-1)(m+n-4),whenmandnareodd\hfill \\ \frac{1}{8}[m{n}^2+m(m-4)n+4],whenmandnareeven\hfill \\ \frac{1}{8}[m{n}^2+(m^2-4m-1)n+4],whenmoddandniseven.\hfill \end{array}\right.$$In another form,

$$B\left(v\right)=\left\{\begin{array}{c}{k}_1{k}_2(k_1+k_2)+\left(\genfrac{}{}{0ex}{}{k_1}{2}\right)+\left(\genfrac{}{}{0ex}{}{k_2}{2=}\right)\text{when}m=2k_1+1,n=2k_2+1\hfill \\ k_1{k}_2(k_1+k_2-2)+\frac{1}{2}\text{when}m=2k_1,n=2k_2\hfill \\ k_1{k}_2(k_1+k_2-1)+\frac{1}{2}{(k_2-1)}^2\text{when}m=2k_1+1,n=2k_2\hfill \end{array}\right.$$

3.4 Product of path and cycle

Consider $G=P_m\square C_n$. Then $G$ has $m$ layers of $C_n$ (also $n$ layers of $P_m$) and it can be embedded on the surface of a cylinder.

Theorem 3.3

Let $G=P_m\square C_n$. Then for $(i,j)\in G$

Case 1

If $(i,j)\in P_m\square C_{2k+1}$ $$B\left[(i,j)\right]=\left(\genfrac{}{}{0ex}{}{k}{2}\right)+i(1+2k)(m-i-1)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)\left[\sum _{r=0}^i(H_{m-i+r}-H_{1+r})+H_{1+i}-H_1\right]$$

Case 2

If $(i,j)\in P_m\square C_{2k}$ $$B\left[(i,j)\right]=\frac{{(k-1)}^2}{2}+2ik(m-i-1)+k^2\left[\sum _{r=0}^i(H_{m-i+r}-H_{1+r})+H_{1+i}-H_1\right]$$

Proof

Let $G=P_m\square C_n$ where $V\left(P_m\right)=\{0,1,\dots ,m-1\}$ and $V\left(C_n\right)=\{0,1,\dots ,n-1\}$. Since each layer of $C_n$ is vertex-transitive, it is enough to find $B\left(v\right)$ for only one layer of $P_m$.

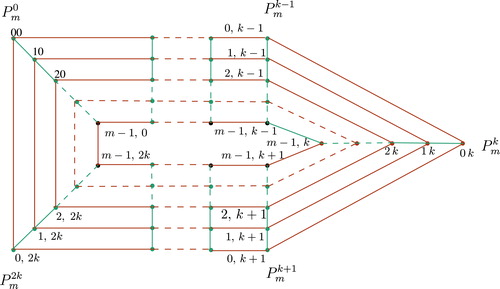
Case 1. When $n$ is odd□

Let $n=2k+1,k\in Z^{+}$. Consider the vertices of $P_m^k$, i.e., $\{(0,k),(1,k),\dots ,(m-1,k)\}$. First consider the vertex $(0,k)$. It is in the outer layer, see Fig. 3.3. There are $2k$ vertices other than $(0,k)$ in this layer. The betweenness centrality of $(0,k)$ is the sum of the contributions of this outer layer $C_n^0$ with itself and with inner layers $C_n^s,\text{for}1\le s\le m-1$. By symmetry, we consider only the $k$ vertices on $C_n^0$, i.e., $\{(0,k-1),(0,k-2),\dots ,(0,0)\}$. Each vertex in $\{(0,k-r),1\le r\le k-1\}$ make pairs with $k-r$ consecutive vertices $(0,k+r),1\le r\le k-1$ of the same layer and give the betweenness centrality ${\sum }_{r=1}^{k-1}(k-r)=\left(\genfrac{}{}{0ex}{}{k}{2}\right)$ to $(0,k)$. i.e., the layer $C_n^0$ contributes $\left(\genfrac{}{}{0ex}{}{k}{2}\right)$ to the betweenness centrality of $(0,k)$.

Fig. 3.3. P_m□C_2k+1.

Now we find the contribution of the outer layer with inner layers. By symmetry, we consider the set of vertices $\{(0,k-r),1\le r\le k-1\}$ of the outer layer making pairs with $k-r$ consecutive vertices of inner layers $\{(q,k+r),1\le r\le k-1,1\le q\le m-1\}$, (i.e., with vertices lying between the layers $P_m^{k+1}$ and $P_m^{2k-r}$ ) and the vertex $\left\{(0,0)\right\}$ making pairs with the vertices of the layer $P_m^k$ except $(0,k)$ and double the value got in these two cases. Since $P_m$ and $C_n$ are geodetic we can use the formula given in Corollary 3.1 to find the number of shortest paths in the product graph. i.e., if $(p,c)\in I\left((p_1,c_1),(p_2,c_2)\right)$ then the contribution of this pair to $(p,c)$ is $$\left(\genfrac{}{}{0ex}{}{|p-p_1|+|c-c_1|}{|p-p_1|}\right)\times \left(\genfrac{}{}{0ex}{}{|p-p_2|+|c-c_2|}{|p-p_2|}\right)\times {\left(\genfrac{}{}{0ex}{}{|p_1-p_2|+|c_1-c_2|}{|p_1-p_2|}\right)}^{-1}$$

If $L_1,L_2,\dots ,L_m$ denote the layers $C_n^0,C_n^1,\dots ,C_n^{m-1}$ respectively. Then the contribution of $L_1$ with other layers to the betweenness centrality of the vertex $(0,k)$ is given by $$(L_1,L_2)\Rightarrow \frac{1}{2}+\frac{1+2}{3}+\frac{1+2+3}{4}+\cdots +\frac{1+2+\cdots +k}{k+1}=\frac{1}{2}\sum _{n=1}^{k}n=\frac{1}{2}\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)$$ $$(L_1,L_3)\Rightarrow \frac{1}{3}+\frac{1+3}{6}+\frac{1+3+6}{10}+\cdots +\frac{1+3+6+\cdots +\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)}{\left(\genfrac{}{}{0ex}{}{k+2}{2}\right)}=\frac{1}{3}\sum _{n=1}^{k}n=\frac{1}{3}\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)$$ $$(L_1,L_4)\Rightarrow \frac{1}{4}+\frac{1+4}{10}+\frac{1+4+10}{20}+\cdots +\frac{1+4+10+\cdots +\left(\genfrac{}{}{0ex}{}{k+2}{3}\right)}{\left(\genfrac{}{}{0ex}{}{k+3}{3}\right)}=\frac{1}{4}\sum _{n=1}^{k}n=\frac{1}{4}\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)$$ etc. $$(L_1,L_m)\Rightarrow \frac{1}{m}+\frac{1+m}{\left(\genfrac{}{}{0ex}{}{m+1}{2}\right)}+\frac{1+m+\left(\genfrac{}{}{0ex}{}{m+1}{2}\right)}{\left(\genfrac{}{}{0ex}{}{m+2}{2}\right)}+\cdots +\frac{1+m+\left(\genfrac{}{}{0ex}{}{m+1}{2}\right)+\cdots +\left(\genfrac{}{}{0ex}{}{k+m-2}{m-1}\right)}{\left(\genfrac{}{}{0ex}{}{k+m-1}{m-1}\right)}=\frac{1}{m}\sum _{n=1}^{k}n=\frac{1}{m}\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)$$ Therefore, if $H_m$ denotes the $m$th harmonic number i.e., $H_m={\sum }_{r=1}^{m}1∕r$ with $H_0=0$, then (8) $$B\left[(0,k)\right]=\left(\genfrac{}{}{0ex}{}{k}{2}\right)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)\sum _{r=2}^m\frac{1}{r}=\left(\genfrac{}{}{0ex}{}{k}{2}\right)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)(H_m-H_1)$$(8)

Consider the vertex $(1,k)$ on $L_2$. Now from Eq. (8) the vertices of $L_2$ with $L_2,L_3,\dots ,L_m$ give the betweenness centrality $\left(\genfrac{}{}{0ex}{}{k}{2}\right)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)(H_{m-1}-H_1)$, and with $L_1$ give $2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)(H_2-H_1)$. Again the vertices of $L_1$ with $L_3,L_4,\dots ,L_m$ give the betweenness centrality $$(m-2)+2\left[\frac{1}{3}(4+5+\cdots kterms)+\frac{1}{4}(5+6+\cdots kterms)+\cdots (m-2)terms\right]=(1+2k)(m-2)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)(H_m-H_2)$$

Combining these we get, $$B\left[(1,k)\right]=\left(\genfrac{}{}{0ex}{}{k}{2}\right)+(1+2k)(m-2)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)(H_{m-1}-H_1+H_m-H_2+H_2-H_1)$$

Similarly, for the vertex $(2,k)$, $L_2$ and $L_1$ with inner layers $L_3,L_4.\dots ,L_m$ contribute betweenness centrality $$(m-3)+2\left[\frac{1}{3}(4+5+\cdots kterms)+\frac{1}{4}(5+6+\cdots kterms)+\cdots (m-3)terms\right]+(m-3)+2\left[\frac{1}{4}(5+6+\cdots kterms)+\frac{1}{5}(5+6+\cdots kterms)+\cdots (m-3)terms\right]=2(1+2k)(m-3)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)(H_m-H_3)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)(H_{m-1}-H_2)$$ Therefore, $$B\left[(2,k)\right]=\left(\genfrac{}{}{0ex}{}{k}{2}\right)+2(1+2k)(m-3)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)(H_{m-2}-H_1+H_{m-1}-H_2+H_m-H_3+H_3-H_1)$$

In general, $$B\left[(t,k)\right]=\left(\genfrac{}{}{0ex}{}{k}{2}\right)+t(1+2k)(m-t-1)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)\left[\sum _{r=0}^t(H_{m-t+r}-H_{1+r})+H_{1+t}-H_1\right]$$By symmetry, $$B\left[(i,j)\right]=\left(\genfrac{}{}{0ex}{}{k}{2}\right)+i(1+2k)(m-i-1)+2\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)\left[\sum _{r=0}^i(H_{m-i+r}-H_{1+r})+H_{1+i}-H_1\right]$$Again, $$B\left[(i,j)\right]=B\left[(m-i-1,j)\right]\text{for}0\le i\le \lceil \frac{m}{2}\rceil -1$$

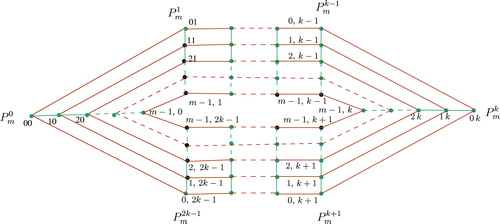
Case 2. When $m$ is even□

Let $m=2k,k\in Z^{+}$. As in Case 1., we can evaluate the betweenness centrality of each vertex on $P_m^k$. But since the graph is even, for each pair of vertices lying on extreme path layers, there are two geodesics joining them and one of them passes through $P_m^k$. So we have to multiply last terms of each expression in Case 1. by $\frac{1}{2}$. See Fig. 3.4

Fig. 3.4. P_m□C_2k.

The contribution of $L_1$ with other layers to the betweenness centrality of the vertex $(0,k)$ is as follows $$(L_1,L_1)\Rightarrow \frac{{(k-1)}^2}{2}$$ $$(L_1,L_2)\Rightarrow \frac{1}{2}+\frac{1+2}{3}+\frac{1+2+3}{4}+\cdots +\frac{1+2+\cdots +k}{k+1}-\frac{1}{2}\frac{1+2+\cdots +k}{k+1}=\frac{1}{2}\sum _{n=1}^{k}n\left[1-\frac{1}{k+1}\right]=\frac{1}{2}\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)-\frac{k}{4}=\frac{k^2}{4}$$ $$(L_1,L_3)\Rightarrow \frac{1}{3}+\frac{1+3}{6}+\frac{1+3+6}{10}+\cdots +\frac{1+3+6+\cdots +\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)}{\left(\genfrac{}{}{0ex}{}{k+2}{2}\right)}-\frac{1}{2}\frac{1+3+6+\cdots +\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)}{\left(\genfrac{}{}{0ex}{}{k+2}{2}\right)}=\frac{1}{3}\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)-\frac{k}{6}=\frac{k^2}{6}$$ $$(L_1,L_4)\Rightarrow \frac{1}{4}+\frac{1+4}{10}+\frac{1+4+10}{20}+\cdots +\frac{1+4+10+\cdots +\left(\genfrac{}{}{0ex}{}{k+2}{3}\right)}{\left(\genfrac{}{}{0ex}{}{k+3}{3}\right)}-\frac{1}{2}\frac{1+4+10+\cdots +\left(\genfrac{}{}{0ex}{}{k+2}{3}\right)}{\left(\genfrac{}{}{0ex}{}{k+3}{3}\right)}=\frac{1}{4}\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)-\frac{k}{8}=\frac{k^2}{8}$$ etc. $$(L_1,L_m)\Rightarrow \frac{1}{m}+\frac{1+m}{\left(\genfrac{}{}{0ex}{}{m+1}{2}\right)}+\frac{1+m+\left(\genfrac{}{}{0ex}{}{m+1}{2}\right)}{\left(\genfrac{}{}{0ex}{}{m+2}{2}\right)}+\cdots +\frac{1+m+\left(\genfrac{}{}{0ex}{}{m+1}{2}\right)+\cdots +\left(\genfrac{}{}{0ex}{}{k+m-2}{m-1}\right)}{\left(\genfrac{}{}{0ex}{}{k+m-1}{m-1}\right)}-\frac{1}{2}\frac{1+m+\left(\genfrac{}{}{0ex}{}{m+1}{2}\right)+\cdots +\left(\genfrac{}{}{0ex}{}{k+m-2}{m-1}\right)}{\left(\genfrac{}{}{0ex}{}{k+m-1}{m-1}\right)}=\frac{1}{m}\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)-\frac{k}{2m}=\frac{k^2}{2m}$$

Therefore, (9) $$B\left[(0,k)\right]=\frac{{(k-1)}^2}{2}+k^2\sum _{r=2}^m\frac{1}{r}=\frac{{(k-1)}^2}{2}+k^2(H_m-H_1)$$(9) Consider the vertex $(1,k)$ on $L_2$. Now from Eq. (9), the vertices of $L_2$ with $L_2,L_3,\dots ,L_m$ give the betweenness centrality $\frac{{(k-1)}^2}{2}+k^2(H_{m-1}-H_1)$, and $L_2$ with $L_1$ give $k^2(H_2-H_1)$. The vertices of $L_1$ with $L_3,L_4,\dots ,L_m$ give the betweenness centrality $$(m-2)+2\left[\frac{1}{3}\left(4+5+\cdots +(k+3)\right)+\frac{1}{4}\left(5+6+\cdots +(k+4)\right)+\cdots +\frac{1}{m}\left((m+1)+(m+2)+\cdots +(m+k)\right)\right]-\left[\frac{k+3}{3}+\frac{k+4}{4}+\cdots +\frac{k+m}{m}\right]=2\left[(m-2)k+\left(\genfrac{}{}{0ex}{}{k+1}{2}\right)(H_m-H_2)\right]-k(H_m-H_2)$$ Combining these we get, $$B\left[(1,k)\right]=\frac{{(k-1)}^2}{2}+2k(m-2)+k^2(H_{m-1}-H_1+H_m-H_2+H_2-H_1)$$Similarly, $$B\left[(2,k)\right]=\frac{{(k-1)}^2}{2}+4k(m-3)+k^2(H_{m-2}-H_1+H_{m-1}-H_2+H_m-H_3+H_3-H_1)$$In general, $$B\left[(t,k)\right]=\frac{{(k-1)}^2}{2}+2tk(m-t-1)+k^2\left[\sum _{r=0}^t(H_{m-t+r}-H_{1+r})+H_{1+t}-H_1\right]$$By symmetry, $$B\left[(i,j)\right]=\frac{{(k-1)}^2}{2}+2ik(m-i-1)+k^2\left[\sum _{r=0}^i(H_{m-i+r}-H_{1+r})+H_{1+i}-H_1\right]$$Again, $$B\left[(i,j)\right]=B\left[(m-i-1,j)\right]\text{for}0\le i\le \lceil \frac{m}{2}\rceil -1\square$$

Corollary 3.6

The graph $P_m\square C_n$ is vertex transitive only when $m=2$ known as cycle prism. The betweenness centrality of cycle prism is given by $$B\left(v\right)=\left\{\begin{array}{c}{k}^2\text{when}n=2k+1\hfill \\ \frac{1}{2}[{(k-1)}^2+k^2]\text{when}n=2k\hfill \end{array}\right.$$

4 Conclusion

A composite graph can be constructed by applying different graph operations on smaller graphs and many of the structural properties of the composite graphs can be studied from its constituent smaller graphs. An expression for the betweenness centrality of Cartesian product of graphs has been derived and examined for different graph products. This can be extended to other graph-products such that an investigation on the behavior of centrality of larger graph can be made from the platform of its constituent smaller graphs.