On transversal and 2-packing numbers in uniform linear systems^☆

Abstract

A linear system is a pair $(P,\mathcal{L})$ where $\mathcal{L}$ is a family of subsets on a ground finite set $P$, such that $|l\cap l^{\prime }|\le 1$, for every $l,l^{\prime }\in \mathcal{L}$. The elements of $P$ and $\mathcal{L}$ are called points and lines, respectively, and the linear system is called intersecting if any pair of lines intersect in exactly one point. A subset $T$ of points of $P$ is a transversal of $(P,\mathcal{L})$ if $T$ intersects any line, and the transversal number, $\tau (P,\mathcal{L})$, is the minimum order of a transversal. On the other hand, a 2-packing set of a linear system $(P,\mathcal{L})$ is a set $R$ of lines, such that any three of them have a common point, then the 2-packing number of $(P,\mathcal{L})$, ${\nu }_2(P,\mathcal{L})$, is the size of a maximum 2-packing set. It is known that the transversal number $\tau (P,\mathcal{L})$ is bounded above by a quadratic function of ${\nu }_2(P,\mathcal{L})$. An open problem is to characterize the families of linear systems which satisfies $\tau (P,\mathcal{L})\le \lambda {\nu }_2(P,\mathcal{L})$, for some $\lambda \ge 1$. In this paper, we give an infinite family of linear systems $(P,\mathcal{L})$ which satisfies $\tau (P,\mathcal{L})={\nu }_2(P,\mathcal{L})$ with smallest possible cardinality of $\mathcal{L}$, as well as some properties of $r$-uniform intersecting linear systems $(P,\mathcal{L})$, such that $\tau (P,\mathcal{L})={\nu }_2(P,\mathcal{L})=r$. Moreover, we state a characterization of 4-uniform intersecting linear systems $(P,\mathcal{L})$ with $\tau (P,\mathcal{L})={\nu }_2(P,\mathcal{L})=4$.

Keywords:

• Linear systems
• Transversal number
• 2-packing number
• Finite projective plane

1 Introduction

A linear system is a pair $(P,\mathcal{L})$ where $\mathcal{L}$ is a family of subsets on a ground finite set $P$, such that $|l\cap l^{\prime }|\le 1$, for every pair of distinct subsets $l,l^{\prime }\in \mathcal{L}$. The linear system $(P,\mathcal{L})$ is intersecting if $|l\cap l^{\prime }|=1$, for every pair of distinct subsets $l,l^{\prime }\in \mathcal{L}$. The elements of $P$ and $\mathcal{L}$ are called points and lines, respectively; a line with exactly $r$ points is called a $r$-line, and the rank of $(P,\mathcal{L})$ is the maximum cardinality of a line in $(P,\mathcal{L})$, when all the lines of $(P,\mathcal{L})$ are $r$ lines we have a $r$-uniform linear system. In this context, a simple graph is a 2-uniform linear system.

A subset $T\subseteq P$ is a transversal (also called vertex cover or hitting set in many papers, as example [1–11]) of $(P,\mathcal{L})$ if for any line $l\in \mathcal{L}$ satisfies $T\cap l\ne 0̸$. The transversal number of $(P,\mathcal{L})$, denoted by $\tau (P,\mathcal{L})$, is the smallest possible cardinality of a transversal of $(P,\mathcal{L})$.

A subset $R\subseteq \mathcal{L}$ is called 2-packing of $(P,\mathcal{L})$ if three elements are chosen in $R$ then they are not incident in a common point. The 2-packing number of $(P,\mathcal{L})$, denoted by ${\nu }_2(P,\mathcal{L})$, is the maximum number of a 2-packing of $(P,\mathcal{L})$.

There are many interesting works studying the relationship between these two parameters, for instance, in [10], the authors propose the problem of bounding $\tau (P,\mathcal{L})$ in terms of a function of ${\nu }_2(P,\mathcal{L})$ for any linear system. In [12], some authors of this paper and others proved that any linear system satisfies: (1) $$\lceil {\nu }_2∕2\rceil \le \tau \le \frac{{\nu }_2({\nu }_2-1)}{2}.$$(1) That is, the transversal number, $\tau$, of any linear system is upper bounded by a quadratic function of their 2-packing number, ${\nu }_2$.

In order to find how a function of ${\nu }_2(P,\mathcal{L})$ can bound $\tau (P,\mathcal{L})$, the authors of [13] using probabilistic methods to prove that $\tau \le \lambda {\nu }_2$ does not hold for any positive $\lambda$. In particular, they exhibit the existence of $k$-uniform linear systems $(P,\mathcal{L})$ for which their transversal number is $\tau (P,\mathcal{L})=n-o\left(n\right)$ and their $2$-packing number is upper bounded by $\frac{2n}{k}$.

Nevertheless, there are some relevant works about families of linear systems in which their transversal numbers are upper bounded by a linear function of their 2-packing numbers. In [14] the authors proved that if $(P,\mathcal{L})$ is a 2-uniform linear system, a simple graph, with $\left|\mathcal{L}\right|>{\nu }_2(P,\mathcal{L})$ then $\tau (P,\mathcal{L})\le {\nu }_2(P,\mathcal{L})-1$; moreover, they characterize the simple connected graphs that attain this upper bound and the lower bound given in Eq. (1). In [12] was proved that the linear systems $(P,\mathcal{L})$ with $\left|\mathcal{L}\right|>{\nu }_2(P,\mathcal{L})$ and ${\nu }_2(P,\mathcal{L})\in \{2,3,4\}$ satisfy $\tau (P,\mathcal{L})\le {\nu }_2(P,\mathcal{L})$; and when they attain the equality, they are a special family of linear subsystems of the projective plane of order $3$, ${\Pi }_3$, with transversal and $2$-packing numbers equal to $4$. Moreover, they proved that $\tau \left({\Pi }_q\right)\le {\nu }_2\left({\Pi }_q\right)$ when ${\Pi }_q=(P_q,{\mathcal{L}}_q)$ is a projective plane of order $q$, consequently the equality holds when q is odd.

The rest of this paper is structured as follows: In Section 2, we present a result about linear systems satisfying $\tau \le {\nu }_2-1$. In Section 3, we give an infinite family of linear systems such that $\tau ={\nu }_2$ with smallest possible cardinality of lines. And, finally, in Section 4, we presented some properties of the $r$-uniform linear systems, such that $\tau ={\nu }_2=r$, and we characterize the $4$-uniform linear systems with $\tau ={\nu }_2=4$.

2 On linear systems with $\tau \le {\nu }_2-1$

Let $(P,\mathcal{L})$ be a linear system and $p\in P$ be a point. It is denoted by ${\mathcal{L}}_p$ to the set of lines incident to $p$. The degree of $p$ is defined as $deg\left(p\right)=\left|{\mathcal{L}}_p\right|$ and the maximum degree overall points of the linear systems is denoted by $\Delta (P,\mathcal{L})$. A point of degrees $2$ and $3$ is called double and triple point, respectively, and two points $p$ and $q$ in $(P,\mathcal{L})$ are adjacent if there is a line $l\in \mathcal{L}$ with $\{p,q\}\subseteq l$.

In this section, we generalize Proposition 2.1, Proposition 2.2, Lemma 2.1, Lemma 3.1 and Lemma 4.1 of [12] proving that a linear system $(P,\mathcal{L})$ with $\left|\mathcal{L}\right|>{\nu }_2(P,\mathcal{L})$ and “few” lines satisfies $\tau (P,\mathcal{L})\le {\nu }_2(P,\mathcal{L})-1$. Notice that, through this paper, all linear systems $(P,\mathcal{L})$ are considered with $\left|\mathcal{L}\right|>{\nu }_2(P,\mathcal{L})$ due to the fact $\left|\mathcal{L}\right|={\nu }_2(P,\mathcal{L})$ if and only if $\Delta (P,\mathcal{L})\le 2$.

Theorem 2.1

Let $(P,\mathcal{L})$ be a linear system with $p,q\in P$ being two points such that $deg\left(p\right)=\Delta (P,\mathcal{L})$ and $deg\left(q\right)=max\{deg\left(x\right):x\in P\setminus \left\{p\right\}\}$. If$\left|\mathcal{L}\right|\le deg\left(p\right)+deg\left(q\right)+{\nu }_2(P,\mathcal{L})-3$, then$\tau (P,\mathcal{L})\le {\nu }_2(P,\mathcal{L})-1$.

Proof

Let $p,q\in P$ be two points as in the theorem, and let ${\mathcal{L}}^{\prime \prime }=\mathcal{L}\setminus \{{\mathcal{L}}_p\cup {\mathcal{L}}_q\}$, which implies that $\left|{\mathcal{L}}^{\prime \prime }\right|\le {\nu }_2(P,\mathcal{L})-2$. Assume that $\left|{\mathcal{L}}^{\prime \prime }\right|={\nu }_2(P,\mathcal{L})-2$ (${\mathcal{L}}_p\cap {\mathcal{L}}_q\ne 0̸$), otherwise, the following set $\{p,q\}\cup \{a_l:a_l\text{is any point of}l\in {\mathcal{L}}^{\prime \prime }\}$ is a transversal of $(P,\mathcal{L})$ of cardinality at most ${\nu }_2(P,\mathcal{L})-1$, and the statement holds. Suppose that ${\mathcal{L}}^{\prime \prime }=\{L_1,\dots ,L_{{\nu }_2-2}\}$ is a set of pairwise disjoint lines because, in otherwise, they induce at least a double point, $x\in P$, hence the following set of points $\{p,q,x\}\cup \{a_l:l\in {\mathcal{L}}^{\prime \prime }\setminus {\mathcal{L}}_x^{\prime \prime }\}$, where $a_l$ is any point of $l$, is a transversal of $(P,\mathcal{L})$ of cardinality at most ${\nu }_2(P,\mathcal{L})-1$, and the statement holds. Let $l_q\in {\mathcal{L}}_q\setminus \left\{l_{p,q}\right\}$ be a fixed line and let $l_p$ be any line of ${\mathcal{L}}_p\setminus \left\{l_{p,q}\right\}$, where $l_{p,q}$ is the line containing to $p$ and $q$ (since ${\mathcal{L}}_p\cap {\mathcal{L}}_q\ne 0̸$). Then $l_p\cap l_q\ne 0̸$, since the $l_q$ induce a triple point on the following 2-packing ${\mathcal{L}}^{\prime \prime }\cup \{l_p,l_{p,q}\}$, which implies that there exists a line $L_{p,q}\in {\mathcal{L}}^{\prime \prime }$ with $l_q\cap l_p\cap L_{p,q}\ne 0̸$, and hence $l_p\cap l_q\ne 0̸$. Consequently, $deg\left(q\right)=\Delta (P,\mathcal{L})$ and $\Delta (P,\mathcal{L})\le {\nu }_2(P,\mathcal{L})-1$ (since $deg\left(p\right)-1\le {\nu }_2(P,\mathcal{L})-2$). Therefore, the following set: $$\{l_p\cap L_i:i=1,\dots ,\Delta -1\}\cup \{a_{\Delta },\dots ,a_{{\nu }_2-2}\}\cup \left\{p\right\},$$where $a_i$ is any point of $L_i$, for $i=\Delta ,\dots ,{\nu }_2-2$, is a transversal of $(P,\mathcal{L})$ of the cardinality at most ${\nu }_2(P,\mathcal{L})-1$, and the statement holds.□

3 A family of uniform linear systems with $\tau ={\nu }_2$

In this section, we exhibit an infinite family of linear systems $(P,\mathcal{L})$ with two points of maximum degree and $\left|\mathcal{L}\right|=2\Delta (P,\mathcal{L})+{\nu }_2(P,\mathcal{L})-2$ with $\tau (P,\mathcal{L})={\nu }_2(P,\mathcal{L})$. It is immediately, by Theorem 2.1, that $\tau (P,\mathcal{L})\le {\nu }_2(P,\mathcal{L})-1$ for linear systems with less lines.

In the remainder of this paper, $(\Gamma ,+)$ is an additive Abelian group with neutral element $e$. Moreover, if ${\sum }_{g\in \Gamma }g=e$, then the group is called neutral sum group. In the following, every group $(\Gamma ,+)$ is a neutral sum group, such that $2g\ne e$, for all $g\in \Gamma \setminus \left\{e\right\}$. As an example of this type of groups we have $({\mathbb{Z}}_n,+)$, for $n\ge 3$ odd.

Let $n=2k+1$, with $k$ a positive integer, and $(\Gamma ,+)$ be a neutral sum group of order $n$. Let: $$\mathcal{L}=\{L_g:g\in \Gamma \setminus \left\{e\right\}\},\text{where}{L}_g=\{(h,g):h\in \Gamma \},$$for $g\in \Gamma \setminus \left\{e\right\}$, and: $${\mathcal{L}}_p=\{l_{p_g}:g\in \Gamma \},\text{where}{l}_{p_g}=\{(g,h):h\in \Gamma \setminus \left\{e\right\}\}\cup \left\{p\right\},$$for $g\in \Gamma$, and ${\mathcal{L}}_q=\{l_{q_g}:g\in \Gamma \}$, where: $$l_{q_g}=\{(h,f_g\left(h\right)):h\in \Gamma ,f_g\left(h\right)=h+g\text{with}{f}_g\left(h\right)\ne e\}\cup \left\{q\right\},$$for $g\in \Gamma$.

Hence, the set of lines $\mathcal{L}$ is a set of pairwise disjoint lines with $\left|\mathcal{L}\right|=n-1$ and each line of $\mathcal{L}$ has $n$ points. On the other hand, ${\mathcal{L}}_p$ and ${\mathcal{L}}_q$ are set of lines incidents to $p$ and $q$, respectively, with $\left|{\mathcal{L}}_p\right|=\left|{\mathcal{L}}_p\right|=n$, and each line of ${\mathcal{L}}_p\cup {\mathcal{L}}_q$ has $n$ points. Moreover, this set of lines satisfies that, giving $l_{p_a}\in {\mathcal{L}}_p$ there exists a unique $l_{q_b}\in {\mathcal{L}}_q$ with $l_{p_a}\cap l_{q_b}=0̸$, otherwise, there exists $l_{p_a}\in {\mathcal{L}}_p$ such that $l_{p_a}\cap l_{q_b}\ne 0̸$, for all $l_{q_b}\in {\mathcal{L}}_q$, which implies that $a+b\in \Gamma \setminus \left\{e\right\}$, for all $b\in \Gamma$, which is a contradiction.

The linear system $(P_n,{\mathcal{L}}_n)$ with $P_n=(\Gamma \times \Gamma \setminus \left\{e\right\})\cup \{p,q\}\text{and}{\mathcal{L}}_n=\mathcal{L}\cup {\mathcal{L}}_p\cup {\mathcal{L}}_q$, denoted by ${\mathcal{C}}_{n,n+1}$, is an $n$-uniform linear system with $n(n-1)+2$ points and $3n-1$ lines. Notice that, this linear system has 2 points of degree $n$ (points $p$ and $q$) and $n(n-1)$ points of degree $3$.

A linear subsystem $(P^{\prime },{\mathcal{L}}^{\prime })$ of a linear system $(P,\mathcal{L})$ satisfies that for any line $l^{\prime }\in {\mathcal{L}}^{\prime }$ there exists a line $l\in \mathcal{L}$ such that $l^{\prime }=l\cap P^{\prime }$, where $P^{\prime }\subset P$. Given a linear system $(P,\mathcal{L})$ and a point $p\in P$, the linear system obtained from $(P,\mathcal{L})$ by deleting the point $p$ is the linear system $(P^{\prime },{\mathcal{L}}^{\prime })$ induced by ${\mathcal{L}}^{\prime }=\{l\setminus \left\{p\right\}:l\in \mathcal{L}\}$. On the other hand, given a linear system $(P,\mathcal{L})$ and a line $l\in \mathcal{L}$, the linear system obtained from $(P,\mathcal{L})$ by deleting the line $l$ is the linear system $(P^{\prime },{\mathcal{L}}^{\prime })$ induced by ${\mathcal{L}}^{\prime }=\mathcal{L}\setminus \left\{l\right\}$. The linear systems $(P,\mathcal{L})$ and $(Q,\mathcal{M})$ are isomorphic, denoted by $(P,\mathcal{L})\simeq (Q,\mathcal{M})$, if after deleting the points of degree 1 or 0 from both, the systems $(P,\mathcal{L})$ and $(Q,\mathcal{M})$ are isomorphic as hypergraphs (see [15]).

It is important to state that in the rest of this paper is considered linear system $(P,\mathcal{L})$ without points of degree one because, if $(P,\mathcal{L})$ is a linear system which has all lines with at least two points of degree 2 or more, and $(P^{\prime },{\mathcal{L}}^{\prime })$ is the linear system obtained from $(P,\mathcal{L})$ by deleting all points of degree one, then they are essentially the same linear system because it is not difficult to prove that transversal and 2-packing numbers of both coincide (see [12]).

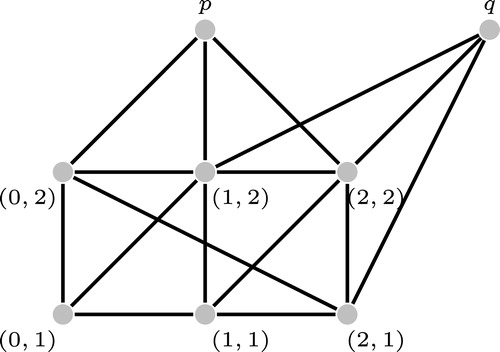
Example 3.1

Let $\Gamma ={\mathbb{Z}}_3$. The linear system ${\mathcal{C}}_{3,4}=(P_3,{\mathcal{L}}_3)$ has as set of points to $P_3=\{(0,1),(1,1),(2,1),(0,2),(1,2),(2,2)\}\cup \left\{p\right\}\cup \left\{q\right\}$ and as set of lines to ${\mathcal{L}}_3=\mathcal{L}\cup {\mathcal{L}}_p\cup {\mathcal{L}}_q$, where $$\mathcal{L}=\{\{(0,1),(1,1),(2,1)\},\{(0,2),(1,2),(2,2)\}\},$$$${\mathcal{L}}_p=\{\{(0,1),(0,2),p\},\{(1,1),(1,2),p\},\{(2,1),(2,2),p\}\},$$$${\mathcal{L}}_q=\{\{(1,1),(2,2),q\},\{(0,1),(1,2),q\},\{(0,2),(2,1),q\}\}$$ and depicted in Fig. 1. This linear system is isomorphic to the linear system giving in [12] Figure 3, which is the linear system with the less number of lines and maximum degree 3 such that $\tau ={\nu }_2=4$.

Fig. 1 Linear system ${\mathcal{C}}_{3,4}=(P_3,{\mathcal{L}}_3)$.

Proposition 3.1

The linear system ${\mathcal{C}}_{n,n+1}$ satisfies that: $$\tau \left({\mathcal{C}}_{n,n+1}\right)=n+1$$

Proof

Notice that $\tau \left({\mathcal{C}}_{n,n+1}\right)\le n+1$ since $\{x_g:x_g\text{is any point of}{L}_g\in \mathcal{L}\}\cup \{p,q\}$ is a transversal of ${\mathcal{C}}_{n,n+1}$. To prove that $\tau (P_n,{\mathcal{L}}_n)\ge n+1$, suppose on the contrary that $\tau (P_n,{\mathcal{L}}_n)=n$. If $T$ is a transversal of cardinality $n$ then $T\subseteq \Gamma \times \Gamma \setminus \left\{e\right\}$, i.e., $p,q⁄\in T$ because, in other case, if $p\in T$ then, by the Pigeonhole principle, there is a line $l_{q_a}\in {\mathcal{L}}_q$ such that $T\cap l_{q_a}=0̸$, since $deg\left(q\right)=n$, which is a contradiction, unless that $q\in T$, which implies that there exists $L\in \mathcal{L}$ such that $L\cap T=0̸$ (because $\left|\mathcal{L}\right|=n-1$), which is also a contradiction. Therefore $T\subseteq \Gamma \times \Gamma \setminus \left\{e\right\}$.

Suppose that: $$T=\{(h_0,f_{g_0}\left(h_0\right)),\dots ,(h_{n-1},f_{g_{n-1}}\left(h_{n-1}\right))\},$$where $\{h_0,\dots ,h_{n-1}\}=\{g_0,\dots ,g_{n-1}\}=\Gamma$ and $f_{g_i}=h_i+g_i\ne e$, for $i=0,\dots ,n-1$. Then: $$\sum _{i=0}^{n-1}{f}_{h_i}\left(g_i\right)=\sum _{i=0}^{n-1}(g_i+h_i)=\sum _{i=0}^{n-1}{g}_i+\sum _{i=0}^{n-1}{h}_i=e,$$since ${\sum }_{g\in \Gamma }g={\sum }_{g\in \Gamma \setminus \left\{e\right\}}g=e$, which implies that there exists $f_{h_j}\left(g_j\right)\in T$ that satisfies $f_{h_j}\left(g_j\right)=e$, which is a contradiction, and consequently $\tau \left({\mathcal{C}}_{n,n+1}\right)=n+1$.□

Proposition 3.2

The linear system ${\mathcal{C}}_{n,n+1}$ satisfies that: $${\nu }_2\left({\mathcal{C}}_{n,n+1}\right)=n+1.$$

Proof

Notice that ${\nu }_2\left({\mathcal{C}}_{n,n+1}\right)\ge n+1$ because, for any two lines $l_{p_g},l_{p_h}\in {\mathcal{L}}_p$, $\mathcal{L}\cup \{l_{p_g},l_{p_h}\}$ is a 2-packing. To prove that ${\nu }_2\left({\mathcal{C}}_{n,n+1}\right)\le n+1$, suppose on the contrary that ${\nu }_2\left({\mathcal{C}}_{n,n+1}\right)=n+2$, and that $R$ is a maximum 2-packing of size $n+2$, we analyze two cases:

Case $\left(i\right)$: Suppose that $R=\mathcal{L}\cup \{l_{p_a},l_{p_b},l_{q_c}\}$, where $l_{p_a},l_{p_b}\in {\mathcal{L}}_p$ and $l_{q_c}\in {\mathcal{L}}_q$; since there is a unique line $l_p\in {\mathcal{L}}_p$ which intersects $l_{q_c}$, then we assume that $l_{p_a}\cap l_{q_c}\ne 0̸$. By construction of ${\mathcal{C}}_{n,n+1}$ there exists $L\in \mathcal{L}$ that satisfies $l_{p_a}\cap l_{q_c}\cap L\ne 0̸$, inducing a triple point, which is a contradiction.

Case $\left(ii\right)$: Let $k$ be an element of $\Gamma \setminus \left\{e\right\}$ and $R=\{l_{p_a},l_{p_b},l_{q_c},l_{q_d}\}\cup \mathcal{L}\setminus \left\{L_k\right\}$ with $l_{p_a},l_{p_b}\in {\mathcal{L}}_p$ and $l_{q_c},l_{q_d}\in {\mathcal{L}}_q$, without loss of generality, suppose that $l_{p_a}\cap l_{q_c}\ne 0̸$, $l_{p_b}\cap l_{q_d}\ne 0̸$, $l_{p_a}\cap l_{q_d}=0̸$ and $l_{p_b}\cap l_{q_c}=0̸$, otherwise, $R$ is not a 2-packing. It is claimed that there exists $L\in \mathcal{L}\setminus \left\{L_k\right\}$ such that either $l_{p_a}\cap l_{q_c}\cap L\ne 0̸$ or $l_{p_b}\cap l_{q_d}\cap L\ne 0̸$, which implies that $R$ induces a triple point, which is contradiction and hence ${\nu }_2\left({\mathcal{C}}_{n,n+1}\right)=n+1$. To verify the claim suppose on the contrary that every $L\in \mathcal{L}\setminus \left\{L_k\right\}$ satisfies $l_{p_a}\cap l_{q_c}\cap L=0̸$ and $l_{p_b}\cap l_{q_d}\cap L=0̸$. It means that $l_{p_a}\cap l_{q_c}\cap L_k\ne 0̸$ and $l_{p_b}\cap l_{q_d}\cap L_k\ne 0̸$. By construction of ${\mathcal{C}}_{n,n+1}$ it follows that: $$l_{p_i}=\{(i,x):x\in \Gamma \setminus \left\{e\right\}\},\text{for all}i\in \Gamma ,$$$$l_{q_j}=\{(x,x+j):x\in \Gamma \setminus \left\{e\right\}\text{and}x+j\ne e\},\text{for all}j\in \Gamma ,\text{and}$$$$L_k=\{(x,k):x\in \Gamma \}.$$

If $l_{p_a}\cap l_{q_c}\cap L_k\ne 0̸$ and $l_{p_b}\cap l_{q_d}\cap L_k\ne 0̸$, then $a+c=b+d=k$. On the other hand, as $l_{p_a}\cap l_{q_d}=0̸$ and $l_{p_b}\cap l_{q_c}=0̸$, then $a+d=b+c=e$. As a consequence of $a+c=b+d=k$ and $a+d=b+c=e$ we obtain $2k=e$, which is a contradiction. Therefore, ${\nu }_2\left({\mathcal{C}}_{n,n+1}\right)=n+1$.□

Hence, by Propositions 3.1 and 3.2 it was proved that:

Theorem 3.2

Let $n=2k+1$, with $k\in \mathbb{N}$, then $$\tau \left({\mathcal{C}}_{n,n+1}\right)={\nu }_2\left({\mathcal{C}}_{n,n+1}\right)=n+1,$$with smallest possible cardinality of lines.

3.1 Straight line systems

A straight line representation on ${\mathbb{R}}^2$ of a linear system $(P,\mathcal{L})$ maps each point $x\in P$ to a point $p\left(x\right)$ of ${\mathbb{R}}^2$, and each line $L\in \mathcal{L}$ to a straight line segment $l\left(L\right)$ of ${\mathbb{R}}^2$ in such a way that for each point $x\in P$ and line $L\in \mathcal{L}$ satisfies $p\left(x\right)\in l\left(L\right)$ if and only if $x\in L$, and for each pair of distinct lines $L,L^{\prime }\in \mathcal{L}$ satisfies $l\left(L\right)\cap l\left(L^{\prime }\right)=\{p\left(x\right):x\in L\cap L^{\prime }\}$. A straight line system $(P,\mathcal{L})$ is a linear system, such that it has a straight line representation on ${\mathbb{R}}^2$. In [12] was proved that the linear system ${\mathcal{C}}_{3,4}$ is not a straight one. The Levi graph of a linear system $(P,\mathcal{L})$, denoted by $B(P,\mathcal{L})$, is a bipartite graph with vertex set $V=P\cup \mathcal{L}$, where two vertices $p\in P$, and $L\in \mathcal{L}$ are adjacent if and only if $p\in L$.

In the same way as in [12] and according to [16], any straight line system is Zykov-planar, see also [17]. Zykov proposed to represent the lines of a set system by a subset of the faces of a planar map on $R^2$, i.e., a set system $(X,\mathcal{F})$ is Zykov-planar if there exists a planar graph $G$ (not necessarily a simple graph) such that $V\left(G\right)=X$ and $G$ can be drawn in the plane with faces of $G$ two-colored (say red and blue) so that there exists a bijection between the red faces of $G$ and the subsets of $\mathcal{F}$ such that a point $x$ is incident with a red face if and only if it is incident with the corresponding subset. In [18] was shown that the Zykov’s definition is equivalent to the following: A set system $(X,\mathcal{F})$ is Zykov-planar if and only if the Levi graph $B(X,\mathcal{F})$ is planar. It is well-known that for any planar graph $G$ the size of $G$, $\left|E\left(G\right)\right|$, is upper bounded by $\frac{k(\left|V\left(G\right)\right|-2)}{k-2}$ (see [19] page 135, exercise 9.3.1 (a)), where $k$ is the girth of $G$ (the length of a shortest cycle contained in the graph $G$). It is not difficult to prove that the Levi graph $B\left({\mathcal{C}}_{n,n+1}\right)$ of ${\mathcal{C}}_{n,n+1}$ is not a planar graph, since the size of the girth of $B\left({\mathcal{C}}_{n,n+1}\right)$ is $6$, it follows: $$3n^2-n=\left|E\left({\mathcal{C}}_{n,n+1}\right)\right|>\frac{3(n^2+2n-1)}{2},$$for all $n\ge 3$. Therefore, the linear system ${\mathcal{C}}_{n,n+1}$ is not a straight line system.

Finally, as a Corollary of Theorem 2.1, we have the following:

Corollary 3.1

Let $(P,\mathcal{L})$ be a straight line system with $p,q\in P$ being two points such that $deg\left(p\right)=\Delta (P,\mathcal{L})$ and $deg\left(q\right)=max\{deg\left(x\right):x\in P\setminus \left\{p\right\}\}$. If$\left|\mathcal{L}\right|\le deg\left(p\right)+deg\left(q\right)+{\nu }_2(P,\mathcal{L})-3$, then$\tau (P,\mathcal{L})\le {\nu }_2(P,\mathcal{L})-1$.

4 Intersecting $r$-uniform linear systems with $\tau ={\nu }_2=r$

In this subsection, we give some properties of $r$-uniform linear systems that satisfy $\tau ={\nu }_2=r$ as well as a characterization of $4$-uniform linear systems with $\tau ={\nu }_2=4$.

Let ${\mathbb{L}}_r$ be the family of intersecting linear systems $(P,\mathcal{L})$ of rank $r$ that satisfies $\tau (P,\mathcal{L})={\nu }_2(P,\mathcal{L})=r$, then we have the following lemma:

Lemma 4.1

Each element of ${\mathbb{L}}_r$ is an $r$-uniform linear system.

Proof

Let us consider $(P,\mathcal{L})\in {\mathbb{L}}_r$ and $l\in \mathcal{L}$ any line of $(P,\mathcal{L})$. It is clear that $T=\{p\in l:deg\left(p\right)\ge 2\}$ is a transversal of $(P,\mathcal{L})$. Hence $r=\tau (P,\mathcal{L})\le \left|T\right|\le r$, which implies that $\left|l\right|=r$, for all $l\in \mathcal{L}$. Moreover, $deg\left(p\right)\ge 2$, for all $p\in l$ and $l\in \mathcal{L}$. □

In [20] was proved the following:

Lemma 4.2

[20] Let $(P,\mathcal{L})$ be an$r$-uniform intersecting linear system then every edge of $(P,\mathcal{L})$ has at most one vertex of degree 2. Moreover $\Delta (P,\mathcal{L})\le r$.

Lemma 4.3

[20] Let $(P,\mathcal{L})$ be an $r$-uniform intersecting linear system then $$3(r-1)\le \left|\mathcal{L}\right|\le r^2-r+1.$$

Hence, by Theorem 2.1 and Lemma 4.3 it follows:

Corollary 4.1

If $(P,\mathcal{L})\in {\mathbb{L}}_r$ then $3(r-1)+1\le \left|\mathcal{L}\right|\le r^2-r+1$.

In [12] was proved that the linear systems $(P,\mathcal{L})$ with $\left|\mathcal{L}\right|>{\nu }_2(P,\mathcal{L})$ and ${\nu }_2(P,\mathcal{L})\in \{2,3,4\}$ satisfy $\tau (P,\mathcal{L})\le {\nu }_2(P,\mathcal{L})$; and when they attain the equality, they are a special family of linear subsystems of the projective plane of order $3$, ${\Pi }_3$ (some of them 4-uniform intersecting linear systems) with transversal and $2$-packing numbers equal to $4$. Recall that a finite projective plane (or merely projective plane) is a linear system satisfying that any pair of points have a common line, any pair of lines have a common point and there exist four points in general position (there are not three collinear points). It is well known that, if $(P,\mathcal{L})$ is a projective plane, there exists a number $q\in \mathbb{N}$, called order of projective plane, such that every point (line, respectively) of $(P,\mathcal{L})$ is incident to exactly $q+1$ lines (points, respectively), and $(P,\mathcal{L})$ contains exactly $q^2+q+1$ points (lines, respectively). In addition to this, it is well known that projective planes of order $q$, denoted by ${\Pi }_q$, exist when $q$ is a power prime. For more information about the existence and the unicity of projective planes see, for instance, [21,22].

Given a linear system $(P,\mathcal{L})$, a triangle $\mathcal{T}$ of $(P,\mathcal{L})$, is the linear subsystem of $(P,\mathcal{L})$ induced by three points in general position (non collinear) and the three lines induced by them. In [12] was defined $\mathcal{C}=(P_{\mathcal{C}},{\mathcal{L}}_{\mathcal{C}})$ to be the linear system obtained from ${\Pi }_3$ by deleting $\mathcal{T}$; also there was defined ${\mathcal{C}}_{4,4}$ to be the family of linear systems $(P,\mathcal{L})$ with ${\nu }_2(P,\mathcal{L})=4$, such that:

(i)	$\mathcal{C}$ is a linear subsystem of $(P,\mathcal{L})$; and
(ii)	$(P,\mathcal{L})$ is a linear subsystem of ${\Pi }_3$,

this is ${\mathcal{C}}_{4,4}=\{(P,\mathcal{L}):\mathcal{C}\subseteq (P,\mathcal{L})\subseteq {\Pi }_3\text{and}{\nu }_2(P,\mathcal{L})=4\}$.

Hence, the authors proved the following:

Theorem 4.1

[12] Let $(P,\mathcal{L})$ be a linear system with ${\nu }_2(P,\mathcal{L})=4$. Then, $\tau (P,\mathcal{L})={\nu }_2(P,\mathcal{L})=4$ if and only if $(P,\mathcal{L})\in {\mathcal{C}}_{4,4}$.

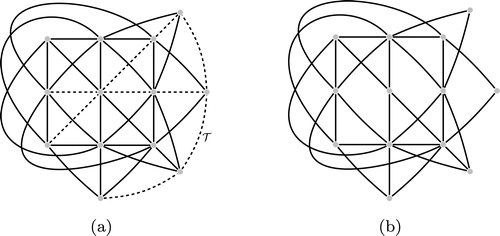
Now, consider the projective plane ${\Pi }_3$ and a triangle $\mathcal{T}$ of ${\Pi }_3$ (see $\left(a\right)$ of Fig. 2). Define $\hat{\mathcal{C}}=(P_{\mathcal{C}},{\mathcal{L}}_{\mathcal{C}})$ to be the linear subsystem induced by ${\mathcal{L}}_{\mathcal{C}}=\mathcal{L}\setminus \mathcal{T}$ (see $\left(b\right)$ of Fig. 2). The linear system $\hat{\mathcal{C}}=(P_{\mathcal{C}},{\mathcal{L}}_{\mathcal{C}})$ just defined has ten points and ten lines. Define ${\hat{\mathcal{C}}}_{4,4}$ to be the family of 4-uniform intersecting linear systems $(P,\mathcal{L})$ with ${\nu }_2(P,\mathcal{L})=4$, such that:

Fig. 2 (a) Projective plane of order 3, ${\Pi }_3$ and (b) Linear system obtained from ${\Pi }_3$ by deleting the lines of the triangle $\mathcal{T}$.

(i)	$\hat{\mathcal{C}}$ is a linear subsystem of $(P,\mathcal{L})$; and
(ii)	$(P,\mathcal{L})$ is a linear subsystem of ${\Pi }_3$,

It is clear that ${\hat{\mathcal{C}}}_{4,4}\subseteq {\mathcal{C}}_{4,4}$ and each linear system $(P,\mathcal{L})\in {\hat{\mathcal{C}}}_{4,4}$ is a 4-uniform intersecting linear system. Hence

Corollary 4.2

$(P,\mathcal{L})\in {\mathbb{L}}_4$ if and only if $(P,\mathcal{L})\in {\hat{\mathcal{C}}}_{4,4}$.

Acknowledgments

The author would like to thank the referees for careful reading and suggestions, which improved the manuscript.