 ?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
We prove that the game-perfect digraphs defined by Andres (2012) with regard to a digraph version of the maker-breaker graph colouring game introduced by Bodlaender (1991) always have a kernel. Furthermore, we introduce weakly game-perfect digraphs related to another digraph version of Bodlaender’s graph colouring game, which was defined by Yang and Zhu (2010), and characterise the classes of weakly game-perfect digraphs by means of the classes of undirected game-perfect graphs.
1 Introduction
In this paper we consider two generalisations of game-perfectness of undirected graphs to digraphs. Before defining these notions we recall the way perfectness of undirected graphs is generalised to digraphs.
1.1 Perfect graphs
An undirected graph is perfect if, for any induced subgraph
of
, the chromatic number
equals the clique number
. The notion of perfectness was introduced by Berge Citation[1]. Perfect graphs are of major importance in computer science, since some problems like the
-colouring problem for
which are NP-hard in general can be solved efficiently on perfect graphs Citation[2]. By the Strong Perfect Graph Theorem Citation[3], a graph is perfect if and only if it does neither have odd holes, which are odd cycles of length
, nor odd antiholes, which are complements of odd holes, as induced subgraphs.
The characterisation of perfect graphs given by the Strong Perfect Graph Theorem is a characterisation by a set of forbidden induced subgraphs. Every hereditary class of graphs (or digraphs) has a characterisation by forbidden induced sub(di)graphs. Made by definition, the class of perfect graphs is hereditary. In a similar way, the classes of digraphs that we will consider in this paper allow characterisations by forbidden induced sub(di)graphs. We aim to discover some of these characterisations.
1.2 Perfect digraphs
The notion of perfectness and the Strong Perfect Graph Theorem have been generalised to digraphs in the following way.
Key of the generalisation is the dichromatic number of a digraph
, which is the smallest number of colours in a (not necessarily proper) colouring of the vertices of
, such that
does not contain any monochromatic directed cycle. The concept of dichromatic number was first introduced by Neumann-Lara Citation[4] and later reinvented by several authors under different names. For example Bokal et al. Citation[5] call it chromatic number of a digraph.
The justification to use the same parameter for the dichromatic number of digraphs as well as for the chromatic number of undirected graphs is given by the observation that any colouring of a symmetric digraph must be proper, thus is a colouring of its underlying undirected graph. The size of a largest symmetric clique of a digraph
is the clique number
of
. A digraph is perfect if, for any induced subdigraph, dichromatic number and clique number coincide. Andres and Hochstättler Citation[6] generalised the Strong Perfect Graph Theorem to digraphs (see Theorem 1 in Section 3).
When one considers digraph classes, the kernel existence problem is a widely-used measure of the complexity of a given class of digraphs Citation[7–9]. Recall that a kernel of a digraph is an independent and absorbing set
, i.e. for every two vertices
we have
and for every vertex
there is a vertex
such that
. It is NP-complete to decide whether a digraph has a kernel, moreover it is even NP-complete to decide whether a perfect digraph has a kernel Citation[6]. However, using Lovász’ (Weak) Perfect Graph Theorem [Citation10] and a major result of Boros and Gurvich [Citation11], Andres and Hochstättler Citation[6] proved that the complement of any perfect digraph has a kernel.
1.3 Game-perfect graphs
The study of special classes of perfect graphs, such as split graphs, bipartite graphs and their complements, comparability graphs, etc., has received considerable attention [Citation12]. Recently studied small classes of perfect graphs are the classes of game-perfect graphs. These are defined via a competitive version of the chromatic number, the so-called game chromatic number, introduced by Bodlaender [Citation13]. This is based on the following graph colouring game, played by two players, Alice and Bob , with a finite undirected graph and a colour set
. At the beginning, every vertex is uncoloured. The players alternately choose an uncoloured vertex
of
and colour it with a colour
from
such that
| (F) | the colour | ||||
The game ends as soon as no such move is possible any more. Alice wins if every vertex is coloured. Otherwise Bob wins. Thus Bob wins if during the game an uncoloured vertex is surrounded by vertices of all colours.
Different variants of the game were considered concerning which player moves first or whether skipping is allowed for a player. For any variant of the game, the game chromatic number
of the graph
is the smallest size of a colour set
such that Alice has a winning strategy for the game played on
with
colours. This parameter is well-defined, since Alice always has a winning strategy with
colours, where
denotes the maximum degree of
. A graph
is game-perfect with regard to the game variant
, or,
-perfect for short, if, for every induced subgraph
of
, we have
.
A structural characterisation of game-perfect graphs by forbidden induced subgraphs has been given for some variants of this game by Andres [Citation14], Lock [Citation15], and Andres and Lock [Citation16].
1.4 Game-perfect digraphs
Two ways of generalising the game-chromatic number from undirected graphs to digraphs have been proposed. We first consider a notion of game-perfectness related to the weak game chromatic number of a digraph
, which is very much inspired by Neumann-Lara’s notion of the dichromatic number. The weak game chromatic number and its underlying game were introduced by Yang and Zhu [Citation17]. The rules of this so-called weak digraph colouring game
(or, weak game, for short) are the same as for the graph colouring game except that the graph
is replaced by a digraph
and the feasibility condition (
) is replaced by the condition
| (Fw) | no monochromatic directed cycles are created. | ||||
The second way to generalise the game-chromatic number is inspired by the importance of neighbourhoods in the graph colouring game and was studied already by Andres Citation[18,19], Yang and Zhu [Citation17], and Chan et al. [Citation20]. In the strong digraph colouring game (or, strong game, for short), the feasibility condition (
) is replaced by
| (Fs) | the colour | ||||
As in the weak game, Alice wins if every vertex is coloured at the end. Then the colour classes are acyclic. But in the strong game Bob wins already if an uncoloured vertex is surrounded by in-neighbours of all colours, even if this partial colouring could be extended to a colouring where all colour classes are acyclic.
As for the game in the undirected case, we may specify the player
who starts and the player
who has the right to skip, where “
” resp. “
” denote Alice resp. Bob and “
” denotes “none of the players”. This defines six different weak games of the form
resp. six different strong games
for digraphs with regard to the associated games
for undirected graphs (see Section 2).
Then for each of these variants we may define the weak resp. strong game chromatic number as the smallest number of colours such that Alice has a winning strategy for this variant of the weak resp. strong digraph colouring game. We define a digraph to be weakly resp. strongly game-perfect if, for any induced subdigraph, weak resp. strong game chromatic number and clique number coincide. In [Citation19], strongly game-perfect digraphs were introduced and the classes of strongly game-perfect biorientations of paths and cycles were characterised.
1.5 Our contribution
This paper initiates the study of weakly game-perfect digraphs and has two main results.
First, we reduce the characterisation of weakly game-perfect digraphs to the characterisation of game-perfect graphs. Together with the characterisations from [Citation14] and Citation[15,16], this gives us complete characterisations of weakly game-perfect digraphs for the games ,
,
and
by forbidden induced subdigraphs.
Second, we show that every strongly game-perfect digraph with regard to the game has a kernel.
The paper is structured as follows. In Section 2 we introduce the notation. In Section 3 we summarise some previous results needed for our proofs. Section 4 contains the characterisation of weakly game-perfect digraphs. Kernels in strongly game-perfect digraphs are studied in Section 5. Implications of our work and open problems are described in the final Section 6.
2 Notation
For all terminology on digraphs we refer to Bang-Jensen and Gutin [Citation21]. All digraphs we consider are without loops and without multiple arcs, however pairs and
of antiparallel arcs are allowed. By
we denote the complement of a digraph
, i.e. the arc set of
consists of all arcs
with
, such that
is not an arc of
. Undirected graphs are considered as symmetric digraphs, i.e. those digraphs where for any arc
there also exists the arc
. A pair
with
is called an edge. An arc
such that
is not an arc is called single arc. For a digraph
, the symmetric digraph
, where
is the union of all edges of
(i.e. the set of all arcs
such that also
), is called symmetric part of
.
A symmetric clique is a symmetric digraph where for every ordered pair of distinct vertices the arc
exists. The clique number
of a digraph
is the size of the largest symmetric clique in
. In line with the undirected case, a digraph
is perfect if, for any induced subdigraph
of
, we have the equality
. A filled odd hole resp. a filled odd antihole is a digraph
such that its symmetric part
is an odd hole resp. an odd antihole. More generally, for any graph
, a filled
is a digraph
with
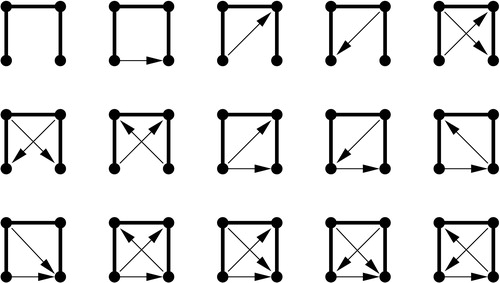
. See for examples. In all depictions, edges
are depicted as fat lines, single arcs
as arrows.
By ,
, and
we denote symmetric cliques, paths and cycles with
vertices, respectively.
and
denote directed paths and directed cycles with
vertices, respectively. The disjoint union
of two graphs
and
is the graph consisting of an isomorphic copy
of
and an isomorphic copy
of
with disjoint vertex sets and no edges between
and
. The join
of
and
is built from
by connecting every vertex of
with every vertex of
by an edge. The disjoint union
of
disjoint copies of the same graph
is denoted as
.
We consider six variants of each of the digraph colouring games, denoted by the symbols and
for the weak and the strong game, respectively, where
, with
and
.
denotes the player who has the first move.
denotes a player that has the right to miss one or several turns at any time of the game, including the first move;
“
” means that none of the players has this right. We also use the abbreviations
and
.
The weak (resp. strong) game chromatic number (resp.
) of a digraph
with regard to the game
(resp.
) is the smallest size
of a colour set
such that Alice has a winning strategy for the weak (resp. strong) digraph colouring game
(resp.
) played on
with colour set
.
We define a digraph to be weakly game-perfect with regard to the game
(or, weakly
-perfect, or
-perfect for short) if, for any induced subdigraph
of
,
. The digraph
is strongly game-perfect with regard to the game
(or, strongly
-perfect, or
-perfect for short) if, for any induced subdigraph
of
,
. Note that for undirected graphs, considered as symmetric digraphs, the games
and
are equal, therefore the notions of weak and strong game chromatic number and thus the notions of weakly and strongly game-perfect coincide. For the games
and
, when played on an undirected graph, we use simply the symbol
. The game
is the original maker-breaker graph colouring game introduced by Bodlaender [Citation13].
3 Observations and previous results
In this section we list some facts that we will use in our proofs.
3.1 Perfect digraphs
Theorem 1
Andres and Hochstättler Citation[6, Cor. 5] A digraph is perfect if and only if it does neither have filled odd holes nor filled odd antiholes nor directed cycles of length as induced subdigraphs.
Theorem 2
Andres and Hochstättler Citation[6, Cor. 13] For any perfect digraph , the complement
has a kernel.
Theorem 1 is the generalisation of the Strong Perfect Graph Theorem to digraphs. As already mentioned in the introduction, Theorem 2 is related to the Weak Perfect Graph Theorem.
3.2 Colouring games
We have the following obvious relations of colouring parameters.
Observation 3
For any digraph and any
,
,
| (a) |
| ||||
| (b) |
| ||||
Observation 4
For any digraph ,
| (a) |
| ||||
| (b) |
| ||||
| (c) |
| ||||
| (d) |
| ||||
By Observation 4, some of the classes of weakly resp. strongly game-perfect digraphs are related in an obvious way, as depicted in . By Observation 3, weakly resp. strongly game-perfect digraphs are, in particular, perfect.
3.3 Characterisations of game-perfect graphs
A structural characterisation of game-perfect graphs by a set of 4, 7, 7, and 15 forbidden induced subgraphs has been given for the games ,
and
in [Citation14] and for the game
in Citation[15,16], respectively. A characterisation for the richest classes, the
-perfect and
-perfect graphs, is still an open problem.
We summarise the characterisations of game-perfect graphs by forbidden induced subgraphs.
Theorem 5
Andres [14, Thm. 3] A graph is
-perfect if and only if it contains no induced
,
,
,
.
Theorem 6
Andres [14, Thm. 7]
| (a) | A graph | ||||
| (b) | A graph | ||||
Theorem 7
Lock [15, Thm. 14], Andres and Lock [16, Thm. 4] A graph is
-perfect if and only if it contains no induced
,
,
,
,
,
,
,
, chair,
(see).
4 Weakly game-perfect digraphs
As we shall see in Theorem 9, the characterisation of weakly game-perfect digraphs with regard to a game can be easily reduced to the characterisation of game-perfect (undirected) graphs with regard to the associated game
.
The proof of Theorem 9 uses basically the same idea as the main theorem for characterising perfect digraphs by means of perfect graphs in Citation[6]. We start with an obvious observation.
Observation 8
In a digraph that contains no directed cycle
with
as an induced subdigraph, every directed cycle has an edge as a chord.
Theorem 9
For a weak game and the associated undirected game
, a digraph
is
-perfect if and only if the following two conditions hold.
| (i) | The symmetric part | ||||
| (ii) |
| ||||
Proof
First, we show that (i) and (ii) are necessary conditions for -perfectness. Assume that (ii) does not hold, i.e. let
contain an induced directed cycle of length at least 3. Then
is not perfect, thus it is not
-perfect. By contraposition, (ii) is necessary for
-perfectness.
Now, in order to prove that (i) is necessary, we may assume that (ii) holds, i.e. does not contain any directed cycles of length at least 3. Assume that (i) does not hold, i.e. let
be a non-
-perfect graph. This means that there exists an induced subdigraph
of
such that Bob has a winning strategy for the game
played on
with
colours. He uses the same strategy for the game
played on the digraph
with
colours. The single arcs do not restrict him in doing so, since whenever he would be forced by his strategy to close a monochromatic directed cycle, then by Observation 8 this cycle would either be a monochromatic edge or have a monochromatic edge as a chord, neither of which is possible in his strategy for the game
on
. Therefore every move of Bob is feasible in the game
until he creates a win for him or forces Alice to do so, which will happen, since his strategy is a winning strategy on
. Therefore
is not
-perfect. By contraposition, (i) is necessary for
-perfectness.
Second, we show that (i) and (ii) imply that is
-perfect. Let
be a
-perfect graph and
not contain any induced directed cycle of length
. Let
be an induced subdigraph of
. Then
is an induced subgraph of
. Thus, Alice has a winning strategy for the game
played on
with
colours. She uses the same strategy for the game
played on
with
colours. Assume Alice is forced by her strategy to close a monochromatic directed cycle. Then by Observation 8 this cycle would either be a monochromatic edge or have a monochromatic edge as a chord, neither of which is possible in her strategy for the game
on
. Therefore every move of Alice is feasible in the game
until she creates a win for her, i.e. every vertex of
is coloured, which will happen, since her strategy is a winning strategy on
. Since
was arbitrarily chosen,
is
-perfect. □
By the characterisations mentioned in Section 3 and Theorem 9 we obtain explicit characterisations for the four classes of weakly -,
-,
- and
-perfect digraphs.
Corollary 10
A digraph is weakly
-perfect if and only if it contains no induced
(
), filled
(see ), filled
(see), filled
, filled
.
Corollary 11
| (a) | A digraph | ||||
| (b) | A digraph | ||||
Corollary 12
A digraph is weakly
-perfect if and only if it contains no induced
(
) and no induced filled
, where
is one of the graphs
,
,
,
,
,
,
,
, chair,
(see).
Proof of Corollaries 10–12
By Theorem 9, is weakly game-perfect if and only if
is a game-perfect graph and
contains no induced
with
. Thus the corollaries follow from the equivalence
where the list
is the list of forbidden subgraphs given in Theorem 5 (in the case of Corollary 10), Theorem 6 (in the case of Corollary 11), and Theorem 7 (in the case of Corollary 12), respectively. □
We remark that game-perfect graphs for the four variants of the game considered above can be described by finitely many forbidden induced subgraphs, whereas perfect graphs, perfect digraphs and weakly game-perfect digraphs require infinitely many forbidden configurations.
5 Existence of kernels in strongly game-perfect digraphs
The existence of kernels in strongly game-perfect digraphs depends on the non-existence of a single configuration, , the complement of a directed 4-cycle. The key for our analysis is the following.
Theorem 13
Let be a strongly
-perfect digraph that does not contain an induced
. Then
is the complement of a perfect digraph.
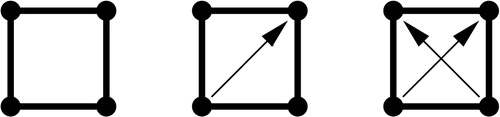
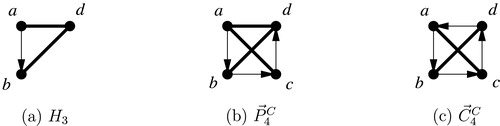
In order to prove Theorem 13 and our second main result, its Corollary 18, we will start with three simple lemmas. Let the digraph that is constructed from the symmetric clique
on the vertices
by deleting the arc
(see (a)).
Lemma 14
The digraph is not
-perfect.
Proof
We will prove that Bob has a winning strategy for the game played on
with
colours. We make a case distinction according to Alice’s first move. Note that the only feasible 2-colouring of
is to colour
in the same colour and
with the other colour. If Alice colours
or
, Bob can easily avoid this situation by colouring the other one of these two vertices with the other colour, thus he wins in this case. If Alice skips or colours
, Bob colours
and wins, since now
must be coloured differently from
by the rules of the strong game. □
Lemma 15
The digraph is not
-perfect.
Proof
This is implied by Lemma 14, since is an induced subdigraph of
(see (b)). □
Lemma 16
The digraph is not
-perfect.
Proof
We will prove that Bob has a winning strategy for the game played on
with
colours. Let the vertices be labelled as in (c). By symmetry, Alice w.l.o.g. colours
in her first move. Then Bob colours
with the other colour. Since
is surrounded by in-neighbours in all colours, Bob wins. □
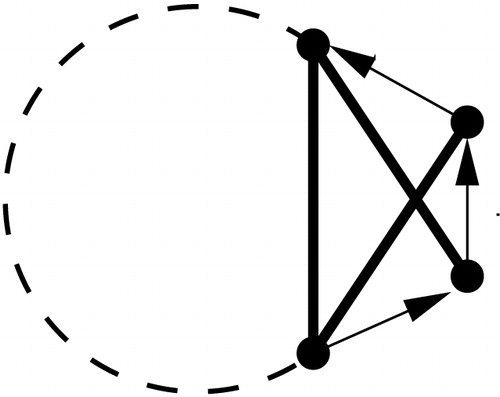
Proof of Theorem 13
is a perfect digraph, since every strongly game-perfect digraph is perfect by Observation 3. By Theorem 1,
has neither an induced filled odd hole nor an induced filled odd antihole nor an induced complement of a directed 3-cycle (since a directed 3-cycle is self-complementary). By precondition,
has no induced complement of a directed 4-cycle. By Lemma 15,
has no complement of a directed
-cycle,
. (Indeed, any four consecutive vertices in a directed cycle
of length
would induce the complement of a directed path
in the complement
of
(see ), which, by Lemma 15, is not
-perfect.) Therefore
is a digraph without induced filled odd hole and without induced filled odd antihole and without induced directed cycles of length
. From Theorem 1 follows that
is perfect. □
Corollary 17
of Theorem 13 Let be a strongly
-perfect digraph that does not contain an induced
. Then
has a kernel.
Proof
Let be a strongly game-perfect digraph (with regard to the game
) that does not contain a
. By Theorem 13,
is perfect. Therefore, by Theorem 2,
has a kernel. □
Corollary 18
Let be a strongly
-perfect digraph. Then
has a kernel.
Proof
By Observation 4, is
-perfect. By Lemma 16,
contains no induced
. Therefore, by Corollary 17,
has a kernel. □
We remark that in the class of -perfect digraphs that contain an induced
there exist members that do not have a kernel, e.g. the
, and members that have a kernel, as shown in Example 19.
Example 19
The digraph from (b), which we call
with roof, is
-perfect and has a kernel.
Proof
The digraph has a kernel: e.g. a kernel consists of the two circled vertices in (b). We have to prove that
is
-perfect, i.e. Alice has a winning strategy for any subdigraph
of
when the game
is played on
with
colours. For the subdigraphs with 0, 1, 2 or 3 vertices such a strategy is trivial. Therefore we are left to consider
and its (up to isomorphism) three subdigraphs of order 4, namely
and the digraphs
and
from .
Alice’s strategy with 3 colours on is the following. We call the vertex that is not in the
roof vertex, its two neighbours base vertices, and the other two vertices diagonal vertices. In her first move, Alice colours the roof vertex with colour 1. If Bob colours a base vertex with colour 2, then Alice colours the other base vertex with colour 3. If Bob colours a diagonal vertex with colour 2, then Alice proceeds in the same way, i.e. she colours the other diagonal vertex with colour 3. Then, in any case one of the remaining vertices can be coloured at least in colour 3 but not in colour 2, the other at least in colour 2 but not in colour 3, thus there is no move of Bob to avoid the digraph getting completely coloured in the remainder of the game. If, otherwise, Bob, in his first move, colours a diagonal vertex
with colour 1, then Alice colours the base vertex that is the in-neighbour of
with colour 2. Also in this case the last two vertices are forced to be coloured feasibly.
Alice’s strategy with 2 colours on is the following. She misses her first turn. Then she replies on Bob’s move as in the preceeding strategy: If Bob colours a vertex with colour 1, she colours the vertex connected to it by an edge with colour 2. This will lead into a winning situation for her by the same arguments as in the case of
.
Alice’s strategy with 3 colours on is the following. She misses her first turn and then follows a copycat strategy: if Bob colours a central vertex, she colours the other central vertex; if Bob colours another vertex with colour
, she colours its non-neighbour with
. This obviously will make her win.
Alice’s strategy with 2 colours on is the following. In her first move she colours the vertex pointed at in with colour 1. If Bob colours its edge-neighbour with colour 2, Alice may colour the central vertex with colour 1 to make Bob complete the colouring. If Bob colours a vertex of the uncoloured edge, Alice colours the other vertex of the uncoloured edge with the other colour. Since the last vertex has no in-neighbour in this edge, it may be coloured in colour 2 anyway. Therefore, Alice wins in any case. □
6 Final remarks
Andres [Citation19] proved that every strongly game-perfect digraph has diameter at most 8. Therefore it is easy to see that the classes of weakly game-perfect digraphs are much richer than the classes of strongly game-perfect digraphs. Indeed, for any game variant and its corresponding weak variant
, every orientation of a forest of diameter greater than 8 is weakly game-perfect, but not strongly game-perfect.
We might ask for a characterisation of strongly game-perfect digraphs. For the games, where Bob begins, this can be easily reduced to the case of undirected graphs, since in these cases the oriented path is not game-perfect (cf. (a)), implying that single arcs are forbidden, thus in these cases we have the following.
Observation 20
Andres [19, Prop. 2] Let . Then every
-perfect digraph is an undirected graph.
The characterisations of game-perfect graphs for the game by a set of 4 forbidden induced subgraphs in Theorem 5 resp. for the game
by a set of 15 forbidden induced subgraphs in Theorem 7 are thus an answer for the characterisation of
- resp.
-perfect digraphs, too.
Problem 21
Characterise the class of -perfect graphs by a set of forbidden induced subgraphs.
Problem 22
Characterise the classes of -,
- resp.
-perfect digraphs by sets of forbidden induced subdigraphs, respectively.
A partial result characterising the strongly game-perfect biorientations of forests has been recently obtained by Andres, Charpentier and Fong [Citation22].
Observation 20 implies immediately also the following.
Corollary 23
Let . Then every strongly
-perfect digraph has a kernel.
By Observation 4, we get from Corollary 18 the following.
Corollary 24
Every strongly -perfect digraph has a kernel.
Problem 25
Characterise which of the strongly -perfect digraphs with a
has a kernel.
As already mentioned, it is NP-complete to decide whether a perfect digraph has a kernel (cf. Citation[6]). In contrast to that we conjecture that the solution to Problem 25 is easy. Conjecture 26 is supported by the observation that, since is forbidden in any strongly game-perfect digraph (cf. (b)), on the one hand only one of the components of a game-perfect digraph is not an undirected graph, and undirected graphs always have a kernel, on the other hand the structure of the non-symmetric component is forced to be quite simple and, thus, might be characterised by finitely many efficient rules.
Conjecture 26
There is a polynomial time algorithm to decide whether a strongly game-perfect digraph has a kernel.
One might also ask which weakly game-perfect digraphs admit a kernel.
Problem 27
Characterise the subclass of digraphs admitting a kernel among the weakly game-perfect digraphs (for the different variants of the game). Or at least, determine the complexity of deciding whether a weakly game-perfect digraph has a kernel.
References
- BergeC.von GraphenFärbung, deren sämtliche bzw. deren ungerade Kreise starr sind (Zusammenfassung) Wissenschaftliche Zeitschrift1961Martin Luther Universität Halle-Wittenberg, mathematisch-naturwissenschaftliche Reihe114–115
- GrötschelM.LovászL.SchrijverA., The ellipsoid method and its consequences in combinatorial optimization Combinatorica 11981 169–197
- ChudnovskyM.RobertsonN.SeymourP.ThomasR., The strong perfect graph theorem Ann. of Math. (2) 1642006 51–229
- Neumann-LaraV., The dichromatic number of a digraph J. Combin. Theory Ser. B 331982 265–270
- BokalD.FijavžG.JuvanM.KayllP.M.MoharB., The circular chromatic number of a digraph J. Graph Theory 462004 227–240
- AndresS.D.HochstättlerW., Perfect digraphs J. Graph Theory 792015 21–29
- BorosE.GurvichV., graphs Perfect. kernels Perfect graphs kernels and cores of cooperative games Discrete Math. 3062006 2336–2354
- FraenkelA.S., Combinatorial game theory foundations applied to digraph kernels Electronic J. Combin. 41997#R10
- Galeana-SánchezH.Sánchez-LópezR., Richardson’s theorem in H-coloured digraphs Graphs Combin. 322016 629–638
- LovászL., Normal hypergraphs and the perfect graph conjecture Discrete Math. 21972 253–267
- BorosE.GurvichV., Perfect graphs are kernel solvable Discrete Math. 1591996 35–55
- GolumbicM.C.Algorithmic Graph Theory and Perfect Graphssecond ed.Annals of Discrete Mathematics vol. 572004ElsevierAmsterdam
- BodlaenderH.L., On the complexity of some coloring games Internat. J. Found. Comput. Sci. 21991 133–147
- AndresS.D., On characterizing game-perfect graphs by forbidden induced subgraphs Contrib. Discrete Math. 72012 21–34
- LockE., The structure of gB-perfect graphs(Bachelor’s Thesis) 2016FernUniversität in Hagen
- S.D. Andres, E. Lock, Characterising and recognising game-perfect graphs, Submitted,https://arxiv.org/abs/1810.12439.
- YangD.ZhuX., Game colouring directed graphs Electron. J. Combin. 172010#R11
- AndresS.D., Lightness of digraphs in surfaces and directed game chromatic number Discrete Math. 3092009 3564–3579
- AndresS.D., Game-perfect digraphs Math. Methods Oper. Res. 762012 321–341
- ChanW.H.ShiuW.C.SunP.K.ZhuX., The strong game colouring number of directed graphs Discrete Math. 3132013 1070–1077
- Bang-JensenJ.GutinG., Digraphs. Theory, Algorithms and Applications2009second ed.London
- S.D. Andres, C. Charpentier, W.L. Fong, Game-perfect directed forests, Unpublished results.

![Fig. 3 Inclusions of the classes of game-perfectness: GP[X,Y] might be the class of either game-perfect graphs or weakly game-perfect digraphs or strongly game-perfect digraphs with regard to game variant [X,Y].](/cms/asset/192e9c9d-9935-4862-8d28-69aac7dc9031/uakc_a_1760670_f0003_b.jpg)
![Fig. 4 Some additional forbidden induced subgraphs in [B,−]-perfect graphs.](/cms/asset/4807d1dd-cb17-4f8d-aaa7-8373ca3c167e/uakc_a_1760670_f0004_b.jpg)
![Fig. 7 Two s[A,A]-perfect digraphs: (a) The C→4C; (b) D0: the C→4C with roof.](/cms/asset/25911a41-95ab-4279-ba42-530836272f89/uakc_a_1760670_f0007_b.jpg)
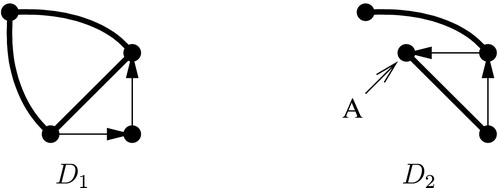
![Fig. 9 (a) P→2 is not [B,Y]-perfect for every Y∈{A,B,−} (b) 2P→2 is not game-perfect for any game.](/cms/asset/d8ea3257-5afa-4ffe-915a-d574d7d458bb/uakc_a_1760670_f0009_b.jpg)