The hyper-Zagreb index of cacti with perfect matchings

Abstract

Let $G$ be a simple connected graph. The hyper-Zagreb index is defined as $HM\left(G\right)={\sum }_{uv\in E\left(G\right)}{(d_G\left(u\right)+d_G\left(v\right))}^2$. A connected graph $G$ is a cacti if all blocks of $G$ are either edges or cycles. Let $\zeta (2n,r)$ be the set of cacti of order $2n$ with a perfect matching and $r$ cycles. In this paper, we determine sharp upper bounds of the hyper-Zagreb index of cacti among $\zeta (2n,r)$ and characterize the corresponding extremal cacti.

Keywords:

• The hyper-Zagreb index
• Cacti
• Perfect matching

1 Introduction

Throughout this paper, all graphs we considered are finite, undirected, and simple. Let $G$ be a connected graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$. Let $\left|G\right|$ and $\left|E\right|$ be the number of vertices and edges of $G$, respectively. For a vertex $u\in V\left(G\right)$, the degree of $u$, denote by $d_G\left(u\right)$ (or $d_u$ for short), is the number of vertices which are adjacent to $u$. Let $N_G\left(u\right)$ be the set of all neighbors of $u$ in $G$. Call a vertex $u$ a $pendant$ $vertex$ of $G$, denote by $PV$ the set of pendent vertices of $G$, if $d_G\left(u\right)=1$ and call an edge $uv$ a $pendant$ $edge$ of $G$, if $d_G\left(u\right)=1$ or $d_G\left(v\right)=1$. Denote by $P_n$ and $C_n$ a path and a cyclic on $n$ vertices, respectively. A subset $M\subseteq E$ is called a matching in $G$ if its elements are edges and no two are adjacent in $G$. A matching in $G$ saturates a vertex $v$, and $v$ is said to be $M-saturated$, if some edge of $M$ is incident with $v$. If every vertex of $G$ is $M-saturated$, the matching $M$ is perfect.

For a molecular graph $G$, the first Zagreb index $M_1\left(G\right)$ and the second Zagreb index $M_2\left(G\right)$ are defined in as $$M_1\left(G\right)=\sum _{u\in V\left(G\right)}{\left(d\left(u\right)\right)}^2$$ $$M_2\left(G\right)=\sum _{uv\in E\left(G\right)}d\left(u\right)d\left(v\right)$$Some recent results on the Zagreb indices are reported in [1–7], where also references to the previous mathematical research in this area can be found.

In 2013, Shirdel et al. in [8] introduced a new degree-topological index named hyper-Zagreb index as $$HM\left(G\right)=\sum _{uv\in E\left(G\right)}{(d_G\left(u\right)+d_G\left(v\right))}^2$$Some recent results on the hyper-Zagreb indices are reported in [9–11].

Recently, finding the extremal values or bounds for the topological index of graphs, as well as related problems of characterizing the extremal graphs, attracted the attention of many researches and many results are obtained. Li et al. [12] determine the n-vertex cacti with maximal Zagreb indices and also determine the cactus with a perfect matching having maximal Zagreb indices. In [13], Du et al. obtain the minimum sum-connectivity indices of trees and unicyclic graphs with given number of vertices and matching number, respectively, and determine the corresponding extremal graphs.

Motivated by these results [12,13], we explore the properties for the hyper-Zagreb index. In this paper, we will determine sharp upper bounds of hyper-Zagreb index among cacti among $\zeta (2n,r)$ and characterize the corresponding extremal cacti.

2 Main results

Firstly, we introduce some useful lemmas which will be used frequently.

Lemma 1

[14] A graph G has a perfect matching if and only if $$o(G-S)\le \left|S\right|forallS\subset V$$where $o(G-S)$ is the number of odd components of $G-S$.

By Lemma 1, we have next corollary.

Corollary 2

A graph G has a perfect matching, then each vertex of G is adjacent to at most one pendent vertex.

In the following, we give sharp upper bounds for hyper-Zagreb index of tree with a perfect matching.

Let $T_{2n}$ be the set of trees of order $2n$ and with a perfect matching.

Lemma 3

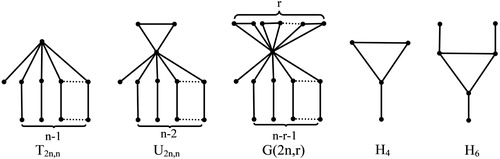
If $T\in T_{2n}$,$n\ge 2$, then$HM\left(T\right)\le \alpha \left(n\right)$ with equality if and only if $T=T_{2n,n}$, where $$\alpha \left(n\right)=n^3+4n^2+11n-12$$and $T_{2n,n}$ is the graph given in Fig. 1.

Fig. 1 Some cacti with a perfect matching.

Proof

By induction on $n$. When $n=2$, the theorem holds clearly.

Next, we assume that $n\ge 3$. Let $M$ be a perfect matching of $T\in T_{2n}$. There exists a vertex $u$ of degree $2$ which is adjacent to a pendent vertex $v$ in $T$.

Let $w$ be the other vertex adjacent to $u$ and $N\left(w\right)\bigcap PV=\{x_1,\dots ,x_t\}$, where $PV$ is the set of all pendent vertices of $T$. Then $t\le 1$ from Corollary 2. If $d\left(w\right)=d$ and $N\left(w\right)\setminus PV=\{x_{t+1},x_{t+2},\dots ,x_{d-1},x_d=u\}$, then $2\le d\le n$ and $d_{x_i}=d_i\ge 2$, $i=t+1,\dots ,d-1$.

Let $T^{\ast }=T-u-v$. then $T^{\ast }\in T_{2n-2}$. By the inductive assumption, $HM\left(T^{\ast }\right)\le \alpha (n-1)$. We know that ${\sum }_{i=1}^{2n}d\left(v_i\right)=2\left|E\right|$, so we have ${\sum }_{i=t+1}^{d-1}{d}_{x_i}+d+3+t+(2n-d-2)\le 2\left|E\right|=4n-2$, so ${\sum }_{i=t+1}^{d-1}{d}_{x_i}\le 2n-t-3$. $$\begin{array}{c}HM\left(T\right)=HM\left(T^{\ast }\right)+t[{(d+1)}^2-d^2]+{(d+2)}^2+\sum _{i=t+1}^{d-1}[{(d+d_{x_i})}^2-{(d+d_{x_i}-1)}^2]+9\hfill \\ \le \alpha (n-1)+3d^2+d+2t+14+2\sum _{i=t+1}^{d-1}{d}_{x_i}\hfill \\ =\alpha \left(n\right)+[\alpha (n-1)-\alpha \left(n\right)]+3d^2+d+2t+14+2\sum _{i=t+1}^{d-1}{d}_{x_i}\hfill \\ \le \alpha \left(n\right)+(-3n^2-5n-8)+3d^2+d+2t+14+2(2n-t-3)\hfill \\ =\alpha \left(n\right)+3(d^2-n^2)+(d-n)\hfill \\ \le \alpha \left(n\right).\hfill \end{array}$$The equality holds if and only if $T=T_{2n,n}$. The proof is completed.□

In the following, we give sharp upper bounds for hyper-Zagreb index of unicyclic graphs with a perfect matching.

Let $U_{2n}$ be the set of unicyclic graphs of order $2n$ and with a perfect matching.

Lemma 4

If $G\in U_{2n}$,$n\ge 2$, then$HM\left(G\right)\le \beta \left(n\right)$ with equality if and only if $G=U_{2n,n}$, where $$\beta \left(n\right)=n^3+7n^2+22n+2$$and $U_{2n,n}$ is the graph given in Fig. 1.

Proof

By induction on $n$.

When $n=2$. It only has the graph $C_4$ and the graph $H_4$. $H_4$ is the graph is the graph given in Fig. 1. $$HM\left(C_4\right)=64<82=HM\left(H_4\right)=\beta \left(2\right)$$

Next, we assume that $n\ge 3$. Let $M$ be a perfect matching of $G\in U_{2n}$.

Case $1$. $\delta \left(G\right)\ge 2$. $$HM\left(C_{2n}\right)=32n<\beta \left(n\right)$$

Case $2$. $\delta \left(G\right)=1$. We divide into two subcases.

Subcase 2.1. There exists a vertex $u$ of degree $2$ which is adjacent to a pendent vertex $v$ in $G$.

Let $w$ be the other vertex adjacent to $u$ and $N\left(w\right)\bigcap PV=\{x_1,\dots ,x_t\}$, where $PV$ is the set of all pendent vertices of $G$. Then $t\le 1$ from Corollary 2. If $d\left(w\right)=d$ and $N\left(w\right)\setminus PV=\{x_{t+1},x_{t+2},\dots ,x_{d-1},x_d=u\}$, then $2\le d\le n+1$ and $d_{x_i}=d_i\ge 2$, $i=t+1,\dots ,d-1$.

Let $G^{\ast }=G-u-v$. then $G^{\ast }\in U_{2n-2}$. By the inductive assumption, $HM\left(G^{\ast }\right)\le \beta (n-1)$. We know that ${\sum }_{i=1}^{2n}d\left(v_i\right)=2\left|E\right|$, so we have ${\sum }_{i=t+1}^{d-1}{d}_{x_i}+d+3+t+(2n-d-2)\le 2\left|E\right|=4n$, so ${\sum }_{i=t+1}^{d-1}{d}_{x_i}\le 2n-t-1$. $$\begin{array}{c}HM\left(G\right)=HM\left(G^{\ast }\right)+t[{(d+1)}^2-d^2]+{(d+2)}^2+\sum _{i=t+1}^{d-1}[{(d+d_{x_i})}^2-{(d+d_{x_i}-1)}^2]+9\hfill \\ \le \beta (n-1)+3d^2+d+2t+14+2\sum _{i=t+1}^{d-1}{d}_{x_i}\hfill \\ =\beta \left(n\right)+[\beta (n-1)-\beta \left(n\right)]+3d^2+d+2t+14+2\sum _{i=t+1}^{d-1}{d}_{x_i}\hfill \\ \le \beta \left(n\right)+(-3n^2-11n-16)+3d^2+d+2t+14+2(2n-t-1)\hfill \\ =\beta \left(n\right)+3d^2+d-3n^2-7n-4\hfill \\ =\beta \left(n\right)+3[d^2-{(n+1)}^2]+d-(n+1)\hfill \\ \le \beta \left(n\right).\hfill \end{array}$$The equality holds if and only if $G=U_{2n,n}$.

Subcase 2.2. The degree of any vertex which is adjacent to a pendent vertex in $G$ is at least $3$.

We denote the cycle $C=u_1{u}_2\dots u_{\lambda }{u}_1$ of $G$. Then $d_{u_i}=3$ if $u$ is adjacent to a pendent vertex, otherwise $d_{u_i}=2$; and $3\le d_{u_1}=d\le n+1$.

Note that at most one of $u_1{u}_2$, $u_1{u}_{\lambda }$ belongs to $M$. Without loss of generality, we assume that $u_1{u}_2⁄\in M$.

$\left(I\right)$ $\lambda =3$.

We know $d_{u_1}=d_{u_2}=d_{u_3}=3$, the graph is $H_6$, which is the graph given in Fig. 1. $$HM\left(H_6\right)=156<\beta \left(3\right)$$

$\left(II\right)$ $\lambda \ge 4$.

$\left(i\right)$ $d_{u_2}=3$. Then there exist a pendent vertex $u_2^{\prime }$ adjacent to $u_2$, and $u_2{u}_2^{\prime }\in M$. $d_{u_3}=3$ or $d_{u_3}=2$.

Let $G^{\ast }=G-u_2-u_2^{\prime }+u_1{u}_3$. $G^{\ast }\in U_{2n-2}$. By the inductive assumption, $HM\left(G^{\ast }\right)\le \beta (n-1)$. $$\begin{array}{c}HM\left(G\right)=HM\left(G^{\ast }\right)+{(d+3)}^2+{(d_{u_3}+3)}^2-{(d_{u_3}+d)}^2+16\hfill \\ \le \beta (n-1)+6d+2d_{u_3}-2d{d}_{u_3}+34\hfill \\ =\beta \left(n\right)+[\beta (n-1)-\beta \left(n\right)]+6d+2d_{u_3}-2d{d}_{u_3}+34\hfill \\ =\beta \left(n\right)+[-3n^2-11n-16]+6d+2d_{u_3}-2d{d}_{u_3}+34\hfill \end{array}$$

If $d_{u_3}=2$, $HM\left(G\right)\le \beta \left(n\right)+2(d-(n+1))-3n^2-9n+24<\beta \left(n\right)$

If $d_{u_3}=3$, $HM\left(G\right)\le \beta \left(n\right)-3n^2-11n+24<\beta \left(n\right)$

$\left(ii\right)$ $d_{u_2}=2$. Since $u_1{u}_2⁄\in M$, $u_2{u}_3\in M$, $d_{u_3}=2$ and $u_3{u}_4⁄\in M$.

Let $G^{\ast }=G-u_3{u}_4+u_2{u}_4$. $G^{\ast }\in U_{2n}$. $$\begin{array}{c}HM\left(G\right)-HM\left(G^{\ast }\right)\hfill \\ =[{(d+2)}^2-{(d+3)}^2]+{(2+d_{u_4})}^2-{(3+d_{u_4})}^2\hfill \\ =-2d-2d_{u_4}-10\hfill \\ <0\hfill \end{array}$$

The proof is completed.□

Now, we give sharp upper bounds for hyper-Zagreb index of cacti with a perfect matching.

Theorem 5

If $G\in \zeta (2n,r)$,$n\ge 2$, then$HM\left(G\right)\le \gamma (n,r)$ with equality if and only if $G(2n,r)$, where $$\gamma (n,r)=(n+r-1){(n+r+2)}^2+{(n+r+1)}^2+9(n-r-1)+16r$$and $G(2n,r)$ is the graph given in Fig. 1.

Proof

By induction on $n+r$.

If $r=0$ or $r=1$. By Lemmas 3 and 4, the theorem holds clearly.

Next, we assume that $n\ge 3$ and $r\ge 2$. Let $M$ be a perfect matching of $G\in \zeta (2n,r)$.

Case $1$. $\delta \left(G\right)\ge 2$.

Since $G\in \zeta (2n,r)$, $d_v\le n+r$ with equality if only if $v$ is the unique common vertex of all cycles of the graph $G(2n,r)$.

Let $C=u_1{u}_2\dots u_{\lambda }{u}_1$ be a cycle of $G$ such that $3\le d_{u_1}=d\le n+r$ and $d_{u_i}=2(i=2,\dots ,\lambda )$, and $N\left(u_1\right)=\{u_2,u_{\lambda },x_1,x_2,\dots ,x_{d-2}\}$. Obviously, at most one of $u_1{u}_2$ and $u_1{u}_{\lambda }$ belongs to $M$. Without loss of generality, we assume that $u_1{u}_2⁄\in M$.

Let $G^{\ast }=G-u_1{u}_2$, then $G^{\ast }\in \zeta (2n,r-1)$. By the inductive assumption, $HM\left(G^{\ast }\right)\le \gamma (n,r-1)$. We know that ${\sum }_{i=1}^{2n}d\left(v_i\right)=2\left|E\right|$, so we have ${\sum }_{i=1}^{d-1}{d}_{x_i}+d+2(2n-d)\le 2\left|E\right|=4n+2r-2$, so ${\sum }_{i=1}^{d-1}{d}_{x_i}\le d+2r-2$. $$\begin{array}{c}HM\left(G\right)=HM\left(G^{\ast }\right)+{(d+2)}^2+\sum _{i=1}^{d-1}[{(d+d_{x_i})}^2-{(d+d_{x_i}-1)}^2]+7\hfill \\ \le \gamma (n,r-1)+2\sum _{i=1}^{d-1}{d}_{x_i}+3d^2+d+12\hfill \\ =\gamma (n,r)+[\gamma (n,r-1)-\gamma (n,r)]+2\sum _{i=1}^{d-1}{d}_{x_i}+3d^2+d+12\hfill \\ \le \gamma (n,r)+[-3{(n+r)}^2-5(n+r)-6]+2(d+2r-2)+3d^2+d+12\hfill \\ =\gamma (n,r)+3[d^2-{(n+r)}^2]+3(d-(n+r))+2(r+1-n)\hfill \\ <\gamma (n,r)\hfill \end{array}$$

Case $2$. $\delta \left(G\right)=1$. We divide into two subcases.

Subcase 2.1. There exists a vertex $u$ of degree $2$ which is adjacent to a pendent vertex $v$ in $G$.

Let $w$ be the other vertex adjacent to $u$ and $N\left(w\right)\bigcap PV=\{x_1,\dots ,x_t\}$, where $PV$ is the set of all pendent vertices of $G$. Then $t\le 1$ from corollary 2.2. If $d\left(w\right)=d$ and $N\left(w\right)\setminus PV=\{x_{t+1},x_{t+2},\dots ,x_{d-1},x_d=u\}$, then $2\le d\le n+r$ and $d_{x_i}=d_i\ge 2$, $i=t+1,\dots ,d-1$.

Let $G^{\ast }=G-u-v$, then $G^{\ast }\in \zeta (2n-2,r)$. By the inductive assumption, $HM\left(G^{\ast }\right)\le \gamma (n-1,r)$. We know that ${\sum }_{i=1}^{2n}d\left(v_i\right)=2\left|E\right|$, so we have ${\sum }_{i=t+1}^{d-1}{d}_{x_i}+d+3+t+(2n-d-2)\le 2\left|E\right|=4n+2r-2$, so ${\sum }_{i=1}^{d-1}{d}_{x_i}\le 2n+2r-t-3$. $$\begin{array}{c}HM\left(G\right)=HM\left(G^{\ast }\right)+t[{(d+1)}^2-d^2]+\sum _{i=t+1}^{d-1}[{(d+d_{x_i})}^2-{(d+d_{x_i}-1)}^2]+{(d+2)}^2+9\hfill \\ \le \gamma (n,r-1)+2\sum _{i=t+1}^{d-1}{d}_{x_i}+2t+3d^2+d+14\hfill \\ =\gamma (n,r)+[\gamma (n,r-1)-\gamma (n,r)]+2\sum _{i=t+1}^{d-1}{d}_{x_i}+2t+3d^2+d+14\hfill \\ \le \gamma (n,r)+[-3{(n+r)}^2-5(n+r)-8]+2(2n+2r-t-3)+3d^2+d+14\hfill \\ =\gamma (n,r)+3[d^2-{(n+r)}^2]+d-(n+r)\hfill \\ \le \gamma (n,r)\hfill \end{array}$$The equality holds if and only if $G=G(2n,r)$.

Subcase 2.2. The degree of any vertex which is adjacent to a pendent vertex in $G$ is at least $3$.

We can choose a cycle $C=u_1{u}_2\dots u_{\lambda }{u}_1$ of $G$ such that $u_i(i=2,3,\dots ,\lambda )$ does not appear on other cycles of $G$. Then $d_{u_i}=3$ if $u$ is adjacent to a pendent vertex, otherwise $d_{u_i}=2$ ; and $3\le d_{u_1}=d\le n+r$.

Note that at most one of $u_1{u}_2$, $u_1{u}_{\lambda }$ belongs to $M$. Without loss of generality, we assume that $u_1{u}_2⁄\in M$.

$\left(I\right)$ $\lambda =3$.

Let $N\left(u_1\right)=\{u_2,u_3,x_1,x_2,\dots ,x_{d-2}\}$, and $d_{x_2}=d_{x_3}=\cdots =d_{x_t}=1$, $0\le t\le 1$, $d_{x_2}\ge 2$, $i=t+1,\dots ,d-2$.

$\left(i\right)$ $d_{u_2}=d_{u_3}=2$. Then $u_2{u}_3\in M$.

Let $G^{\ast }=G-u_2-u_3$. then $G^{\ast }\in \zeta (2n-2,r-1)$. By the inductive assumption, $HM\left(G^{\ast }\right)\le \gamma (n-1,r-1)$. We know that ${\sum }_{i=1}^{2n}d\left(v_i\right)=2\left|E\right|$, so we have ${\sum }_{i=1}^{d-2}{d}_{x_i}+d+4+2n-d-1\le 2\left|E\right|=4n+2r-2$, so ${\sum }_{i=1}^{d-1}{d}_{x_i}\le 2n+2r-5$. $$\begin{array}{c}HM\left(G\right)=HM\left(G^{\ast }\right)+\sum _{i=1}^{d-2}[{(d+d_{x_i})}^2-{(d+d_{x_i}-2)}^2]+2{(d+2)}^2+16\hfill \\ \le \gamma (n-1,r-1)+4\sum _{i=1}^{d-2}{d}_{x_i}+6d^2-4d+32\hfill \\ =\gamma (n,r)+[\gamma (n-1,r-1)-\gamma (n,r)]+4\sum _{i=1}^{d-2}{d}_{x_i}+6d^2-4d+32\hfill \\ \le \gamma (n,r)+[-6{(n+r)}^2-4(n+r)-12]+4(2n+2r-5)+6d^2-4d+32\hfill \\ =\gamma (n,r)+6[d^2-{(n+r)}^2]+4(n+r-d)\hfill \\ \le \gamma (n,r)\hfill \end{array}$$The equality holds if and only if $G=G(2n,r)$.

$\left(ii\right)$ $d_{u_2}=d_{u_3}=3$. Then there exist two pendent vertices $u_2^{\prime }$, $u_3^{\prime }$ adjacent to $u_2$, $u_3$, respectively, and $u_2{u}_2^{\prime }\in M$, $u_3{u}_3^{\prime }\in M$.

Let $G^{\ast }=G-u_2^{\prime }-u_3^{\prime }$. Then $(M\bigcup \left\{u_2{u}_3\right\})\setminus \{u_2{u}_2^{\prime },u_3{u}_3^{\prime }\}$ is a perfect matching of $G^{\ast }$, then $G^{\ast }\in \zeta (2n-2,r)$. By the inductive assumption, $HM\left(G^{\ast }\right)\le \gamma (n-1,r)$. $$\begin{array}{c}HM\left(G\right)=HM\left(G^{\ast }\right)+2({(d+3)}^2-{(d+2)}^2)+52\hfill \\ \le \gamma (n-1,r)+4d+62\hfill \\ =\gamma (n,r)+[\gamma (n-1,r)-\gamma (n,r)]+4d+62\hfill \\ \le \gamma (n,r)+(-3{(n+r)}^2-5(n+r)-8)+4d+62\hfill \\ =\gamma (n,r)+4[d-(n+r)]-3{(n+r)}^2-(n+r)+54\hfill \\ <\gamma (n,r)\hfill \end{array}$$

$\left(iii\right)$ $d_{u_2}=3$, $d_{u_3}=2$, or $d_{u_2}=2$, $d_{u_3}=3$.

Without loss of generality, we assume that $d_{u_2}=3$, $d_{u_3}=2$, Then there exist a pendent vertex $u_2^{\prime }$ adjacent to $u_2$, and $u_2{u}_2^{\prime }\in M$ and $u_1{u}_3\in M$.

Let $N\left(u_1\right)=\{u_2,u_3,x_1,x_2,\dots ,x_{d-2}\}$, and $G^{\ast }=G-u_2-u_2^{\prime }$. Then $d_{x_i}\ge 2$, $i=1,2,\dots ,d-2$ since $u_1{u}_3\in M$, $G^{\ast }\in \zeta (2n-2,r-1)$. By the inductive assumption, $HM\left(G^{\ast }\right)\le \gamma (n-1,r-1)$. We know that ${\sum }_{i=1}^{2n}d\left(v_i\right)=2\left|E\right|$, so we have ${\sum }_{i=1}^{d-2}{d}_{x_i}+d+6+(2n-d-2)\le 2\left|E\right|=4n+2r-2$, so ${\sum }_{i=1}^{d-1}{d}_{x_i}\le 2n+2r-6$. $$\begin{array}{c}HM\left(G\right)=HM\left(G^{\ast }\right)+\sum _{i=1}^{d-2}[{(d+d_{x_i})}^2-{(d+d_{x_i}-1)}^2]+({(d+2)}^2-d^2)+{(d+3)}^2+41\hfill \\ \le \gamma (n-1,r-1)+2\sum _{i=1}^{d-2}{d}_{x_i}+3d^2+5d+56\hfill \\ =\gamma (n,r)+[\gamma (n-1,r-1)-\gamma (n,r)]+2\sum _{i=1}^{d-2}{d}_{x_i}+3d^2+5d+56\hfill \\ \le \gamma (n,r)-6{(n+r)}^2-4(n+r)-12+2(2n+2r-6)+3d^2+5d+56\hfill \\ =\gamma (n,r)+3[d^2-{(n+r)}^2]-3{(n+r)}^2+5d+32\hfill \\ <\gamma (n,r)\hfill \end{array}$$

$\left(II\right)$ $\lambda \ge 4$.

$\left(i\right)$ $d_{u_2}=3$. Then there exist a pendent vertex $u_2^{\prime }$ adjacent to $u_2$, and $u_2{u}_2^{\prime }\in M$. $d_{u_3}=3$ or $d_{u_3}=2$.

Let $G^{\ast }=G-u_2-u_2^{\prime }+u_1{u}_3$. $G^{\ast }\in \zeta (2n-2,r)$. By the inductive assumption, $HM\left(G^{\ast }\right)\le \gamma (n-1,r)$. $$\begin{array}{c}HM\left(G\right)=HM\left(G^{\ast }\right)+{(d+3)}^2+{(d_{u_3}+3)}^2-{(d+d_{u_3})}^2+16\hfill \\ \le \gamma (n-1,r)+6d+6d_{u_3}-2d{d}_{u_3}+34\hfill \\ =\gamma (n,r)+[\gamma (n-1,r)-\gamma (n,r)]+6d+6d_{u_3}-2d{d}_{u_3}+34\hfill \\ =\gamma (n,r)+[-3{(n+r)}^2-5(n+r)-8]+6d+6d_{u_3}-2d{d}_{u_3}+34\hfill \\ =\gamma (n,r)+[(6-2d_{u_3})d-2(n+r)]-3{(n+r)}^2-3(n+r)+6d_{u_3}+26\hfill \\ <\gamma (n,r).\hfill \end{array}$$

$\left(ii\right)$ $d_{u_2}=2$. Since $u_1{u}_2⁄\in M$, $u_2{u}_3\in M$, $d_{u_3}=2$ and $u_3{u}_4⁄\in M$.

Let $G^{\ast }=G-u_3{u}_4+u_2{u}_4$. $G^{\ast }\in \zeta (2n,r)$. $$\begin{array}{c}HM\left(G\right)-HM\left(G^{\ast }\right)=[{(d+2)}^2-{(d+3)}^2]+{(d_{u_4}+2)}^2-{(d_{u_4}+3)}^2<0\hfill \end{array}$$

The proof is completed.□