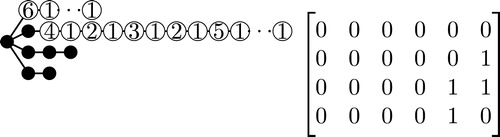Graphs with large rank numbers and rank numbers of subdivided stars

Abstract

A $k$-ranking of a graph $G$ is a function $f:V\left(G\right)\to \{1,2,\dots ,k\}$ such that if $f\left(u\right)=f\left(v\right)$ then every $uv$ path contains a vertex $w$ such that $f\left(w\right)>f\left(u\right)$. The rank number of $G$, denoted ${\chi }_r\left(G\right)$, is the minimum $k$ such that a $k$-ranking exists for $G$. It is known that given a graph $G$ and a positive integer $t$ the question of whether ${\chi }_r\left(G\right)\le t$ is NP-complete. In this paper we characterize graphs with large rank numbers. In addition, we characterize subdivided stars based on their rank numbers.

Keywords:

• Vertex ranking
• Rank number
• Stars
• Subdivided stars

1 Introduction

Let $G$ be an undirected graph with no loops and no multiple edges. A function $f:V\left(G\right)\to \{1,2,\dots ,k\}$ is a (vertex) $k$-ranking of $G$ if for $u,v\in V\left(G\right)$, $f\left(u\right)=f\left(v\right)$ implies that every $uv$ path contains a vertex $w$ such that $f\left(w\right)>f\left(u\right)$. By definition, every ranking is a proper coloring. The rank number of $G$, denoted ${\chi }_r\left(G\right)$, is the minimum value of $k$ such that $G$ has a $k$-ranking. For a graph $G$, by optimal $k$-ranking we mean a $k$-ranking such that $k={\chi }_r\left(G\right)$. When the value of $k$ is not important, we will call a $k$-ranking simply a ranking. It is known that ${\chi }_r\left(K_n\right)=n$ and ${\chi }_r\left(K_{m,n}\right)=min(m,n)+1$.

Vertex rankings of graphs are applicable to a plethora of other fields including designs of very large scale integration (VLSI) layouts, Cholesky factorizations of matrices in parallel, wi-fi analytics, and scheduling problems of assembly steps in manufacturing systems. The optimal tree node ranking problem is identical to the problem of generating a minimum height node separator tree for a tree. Node separator trees are extensively used in VLSI layout [1]. Ranking of graphs is used in communication networks in which information flow between the nodes has to be monitored. An application of graph ranking to scheduling of assembly steps in manufacturing system is discussed in [2].

The concept of ranking was introduced by Iyer et al., in [3], for trees. It is shown by Bodlaender et al., in [4], that for a graph $G$ and a positive integer $t$ the question of whether ${\chi }_r\left(G\right)\le t$ is NP-complete. The mathematical studies of vertex rankings were initiated by Ghoshal and Laskar in [5]. Since then, the rank number of numerous families of graphs have been established, for example see [6–14]. A generalization of $k$-ranking using the $l_p$ norm is discussed in [15].

Let $G$ be a graph of order $n$. We know that $1\le {\chi }_r\left(G\right)\le n$. In this paper, we study the rankings of subdivided stars and identify graphs with large rank numbers. The rank number of a subdivided star is either ${\chi }_r\left(P\right)$ or ${\chi }_r\left(P\right)+1$, where $P$ is the longest path in the subdivided star. We characterize subdivided stars based on their rank numbers, and hence establish the rank number of a subdivided star. We also identify graphs with rank number $n-1$ or $n-2$.

Let $G$ be a graph and let $H$ be a subgraph of $G$. Throughout this paper, the graph $G-H$ represents the graph obtained by deleting $E\left(H\right)$ from $G$. If $S\subseteq V\left(G\right)$, then $G-S$ denotes the graph obtained by deleting the vertices in $S$ from $G$, that is, the subgraph induced by $V\left(G\right)-S$. For any labeling $f$ of a graph $G$, let $S_i\left(f\right)=\{v\in V\left(G\right)\mid f\left(v\right)=i\}$. Throughout this paper, we assume that for any optimal $k$-ranking $f$, $\left|S_i\left(f\right)\right|\ge \left|S_j\left(f\right)\right|$ for $1\le i<j\le k$ because of Lemma 1.1.

Lemma 1.1

[5] There is an optimal ranking $f$ of $G$ such that $\left|S_1\left(f\right)\right|\ge \left|S_2\left(f\right)\right|\ge \cdots \left|S_k\left(f\right)\right|$.

Lemma 1.2

[5] Let $H$ be a subgraph of $G$. Then ${\chi }_r\left(H\right)\le {\chi }_r\left(G\right)$.

Lemma 1.3

[14] Let $H_1$ and$H_2$ be two vertex disjoint graphs such that ${\chi }_r\left(H_1\right)={\chi }_r\left(H_2\right)=k$. Let $G$ be a connected supergraph of $H_1\cup H_2$. Then ${\chi }_r\left(G\right)\ge k+1$.

Lemma 1.4

[5] Let $G$ be a graph of order $n$ and let$I$ be an independent set of $G$. Then ${\chi }_r\left(G\right)\le n-\left|I\right|+1$.

Theorem 1.5

[4] ${\chi }_r\left(P_n\right)=\lfloor {log}_{2}n\rfloor +1$, where$P_n$ is a path on $n$ vertices.

2 Subdivided stars

Let $r$ be a positive integer, and let $n_1,n_2,\dots ,n_r$ be positive integers. Let the edges of a complete bipartite graph $K_{1,r}$ be $e_1,e_2,\dots ,e_r$. For $1\le i\le r$, subdivide edge $e_i$ $n_i-1$ times to obtain a subdivided star denoted by $S_{n_1,n_2,\dots ,n_r}$. We consider the subdivided edges as paths, $P_{n_1},P_{n_2},\dots ,P_{n_r}$, and refer to them as branches.

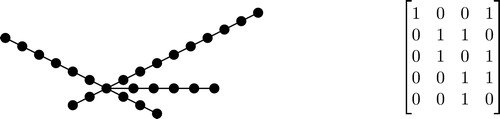
We can use a binary matrix to represent a subdivided star. For a subdivided star, $S_{n_1,n_2,\dots ,n_r}$, where $n_1\ge n_2,\ge \cdots ,\ge n_r$, construct an $r\times {\chi }_r\left(P_{n_1}\right)$ matrix $C$ where row $i$ is the binary representation of $n_i$. An example of a subdivided star and its associated matrix $C$ is given in Fig. 1. Using this binary representation of subdivided stars, we characterize subdivided stars based on their rank numbers.

Fig. 1 $S_{9,6,5,3,2}$ with corresponding matrix $C$.

Lemma 2.1

${\chi }_r\left(P_{n_1}\right)\le {\chi }_r\left(S_{n_1,n_2,\dots ,n_r}\right)\le {\chi }_r\left(P_{n_1}\right)+1$, where $n_1\ge n_2\ge \cdots \ge n_r$.

Proof

Since $P_{n_1}$ is a subgraph of $S_{n_1,n_2,\dots ,n_r}$, ${\chi }_r\left(S_{n_1,n_2,\dots ,n_r}\right)\ge {\chi }_r\left(P_{n_1}\right)$.

Label the center vertex ${\chi }_r\left(P_{n_1}\right)+1$, and branch $P_{n_i}$ using labels $1,2,\dots ,{\chi }_r\left(P_{n_i}\right)$. Since $n_1\ge n_2\ge \cdots \ge n_r$, this will produce a ranking using ${\chi }_r\left(P_{n_1}\right)+1$ labels. Thus ${\chi }_r\left(S_{n_1,n_2,\dots ,n_r}\right)\le {\chi }_r\left(P_{n_1}\right)+1$.□

Theorem 2.2

For any subdivided star $S_{n_1,n_2,\dots ,n_r}$, with $n_1\ge n_2\ge \cdots \ge n_r$, $${\chi }_r\left(S_{n_1,n_2,\dots ,n_r}\right)=\left\{\begin{array}{cc}{\chi }_r\left(P_{n_1}\right),\hfill & \text{if}\exists i\text{such that}{C}_i={[0,0,\dots ,0]}^T\hfill \\ \hfill & \text{and}\forall j<i,C_j\text{contains at most one}1\hfill \\ \hfill & \hfill \\ {\chi }_r\left(P_{n_1}\right)+1,\hfill & \text{otherwise}.\hfill \end{array}\right.$$

Proof

Note that, since ${\chi }_r\left(P_n\right)=\lfloor {log}_{2}n\rfloor +1$ and $P_{n_1}$ is a longest branch, the column $C_1$ will contain at least one 1. Assume that for some $i$, $C_i={[0,0,\dots ,0]}^T$ and $\forall$ $j<i$, $C_j$ contains exactly one $1$. If ${\chi }_r\left(P_{n_1}\right)={\chi }_r\left(P_{n_2}\right)$, then there would be two 1’s in the first column of $C$, which contradicts the assumption. Thus branch $P_{n_1}$ is the only branch with rank number ${\chi }_r\left(P_{n_1}\right)$.

Let $S^1=S_{n_1,n_2,\dots ,n_r}$ and $C^1=C$. Label the outermost $2^{{\chi }_r\left(P_{n_1}\right)-1}-1$ vertices in $P_{n_1}$ with ${\chi }_r\left(P_{n_1}\right)-1$ labels. Label the next outermost vertex, $w_1$, with label ${\chi }_r\left(P_{n_1}\right)$. We have now labeled $2^{{\chi }_r\left(P_{n_1}\right)-1}$ vertices on the branch $P_{n_1}$ so the number of vertices left unlabeled has the same binary representation as $\left|V\left(P_{n_1}\right)\right|$ but without the leading $1$. Remove the $2^{{\chi }_r\left(P_{n_1}\right)-1}$ labeled vertices on $P_{n_1}$ from $S^1$. Now we have a new subdivided star, $S^2=S_{m_1,m_2,\dots ,m_k}$ for $0\le k\le r$, where $m_1\ge m_2\ge \cdots \ge m_k$. Note that any path between vertices in $S^2$ and the deleted vertices from $S^1$ must contain the vertex labeled ${\chi }_r\left(P_{n_1}\right)$. Also, ${\chi }_r\left(P_{m_1}\right)={\chi }_r\left(P_{n_1}\right)-1$, since $C_1$ has exactly one $1$. The matrix $C^2$ can be considered a $r\times {\chi }_r\left(P_{n_1}\right)$ matrix with the first column consisting of all zeros and the last ${\chi }_r\left(P_{n_1}\right)-1$ columns the same as that of $C$. Repeat this process until we get the $C^i$ matrix. The matrix $C^i$ will have zeros on the first $i$ columns and the last ${\chi }_r\left(P_{n_1}\right)-i$ columns the same as that of $C$. Note that column $C_i$ of $C$ has all zeros.

At this point none of the branches of the subdivided star $S^i$ have a rank number greater than ${\chi }_r\left(P_{n_1}\right)-i$, (because the first $i$ columns of $C^i$ are zeros), where $P_{n_1}$ is the longest branch of the original subdivided star $S$. Label the branches of $S^i$ using ${\chi }_r\left(P_{n_1}\right)-i$ labels or less and label the middle vertex ${\chi }_r\left(P_{n_1}\right)-i+1$.

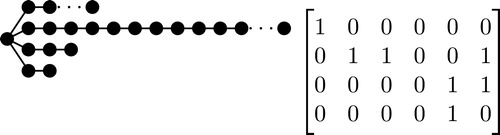
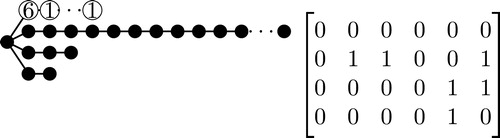
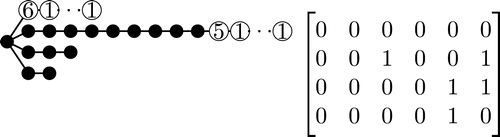
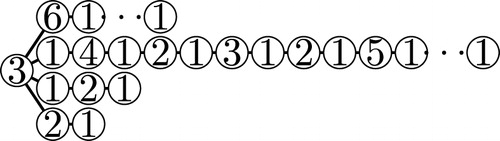
An example of this procedure is shown in Figs. 2–6. Note that in each of these figures the vertices with labels are the vertices that were deleted from the previous subdivided star.

Now any path between vertices in $S^a$ and the vertices deleted from $S^{a+1}$ must contain the largest labeled vertex, $w_a$, that was deleted from the largest branch of $S^a$. Also note that $S^{a+1}$ will not have a vertex labeled the same as the label of $w_a$ because there is exactly one $1$ in each of the first $i-1$ columns of $C$. Therefore, this labeling will create a ranking using only ${\chi }_r\left(P_{n_1}\right)$ labels. This implies ${\chi }_r\left(S_{n_1,n_2,\dots ,n_r}\right)\le {\chi }_r\left(P_{n_1}\right)$, and hence, by Lemma 2.1, ${\chi }_r\left(S_{n_1,n_2,\dots ,n_r}\right)={\chi }_r\left(P_{n_1}\right)$.

Let ${\chi }_r\left(S_{n_1,n_2,\dots ,n_r}\right)={\chi }_r\left(P_{n_1}\right)$ and let $f$ be an optimal labeling of $S$. Assume there is no $i$ such that $C_i={[0,0,\dots ,0]}^T$ and $\forall$ $j<i$, $C_j$ contains only one 1. Let column $C_{g+1}$ contain more than one 1 where $0\le g\le {\chi }_r\left(P_{n_1}\right)-1$. Let $C_1,C_2,C_3,\dots ,C_g$ contain exactly one 1.

If $g=0$, then ${\chi }_r\left(P_{n_1}\right)={\chi }_r\left(P_{n_2}\right)$. Then by Lemma 1.3, ${\chi }_r\left(S_{n_1,n_2,\dots ,n_r}\right)={\chi }_r\left(P_{n_1}\right)+1$, a contradiction.

Suppose $0<g\le {\chi }_r\left(P_{n_1}\right)-1$. Then, since $f$ must use label ${\chi }_r\left(P_{n_1}\right)$ on the branch $P_{n_1}$, and the largest label can only be used once, $f\left(m\right)<{\chi }_r\left(P_{n_1}\right)$, where $m$ is the middle vertex. When optimally ranking $S_{n_1,n_2,\dots ,n_r}$, the vertex with the highest label of any branch can be placed as close to the middle vertex as possible while still maintaining optimality. Therefore, without loss of generality, assume that $f$ has such property.

Now, follow the process defined earlier to create the subdivided star $S^{g+1}$ and matrix $C^{g+1}$ whose first $g$ columns contain zeros and the remaining ${\chi }_r\left(P_{n_1}\right)-g$ columns are the same as that of $C$. Note that in this process, the rank number of the largest branch in $S^{a+1}$ is one less than the rank number of the longest branch in $S^a$ where $1\le a\le g$ (because the first $g$ columns of $C$ have exactly one 1). Thus the longest branch of $S^g$ will have rank number ${\chi }_r\left(P_{n_1}\right)-g+1$, and thus $f\left(m\right)<{\chi }_r\left(P_{n_1}\right)-g+1$. However, the column $C_{g+1}$ has at least two $1^{\prime }$s, which means that there are at least two branches of $S^{g+1}$ with rank number ${\chi }_r\left(P_{n_1}\right)-g$. Then $f\left(m\right)\ge {\chi }_r\left(P_{n_1}\right)-g+1$, a contradiction.

If every column of $C$ has exactly one $1$, then using the above process we get $f\left(m\right)<1$ which is a contradiction.

Thus there is an $i$ such that $C_i={[0,0,\dots ,0]}^T$ and $\forall$ $j<i$, $C_j$ contains only one 1.□

Fig. 2 $S=S^1=S_{32,25,3,2}$ with corresponding matrix $C=C^1$.

Fig. 3 $S^2=S_{25,3,2}$ with corresponding matrix $C^2$.

Fig. 4 $S^3=S_{9,3,2}$ with corresponding matrix $C^3$.

Fig. 5 $S^4=S_{3,2,1}$ with corresponding matrix $C^4$.

Fig. 6 ${\chi }_r\left(S_{32,25,3,2}\right)={\chi }_r\left(P_{32}\right)=6$.

3 Graphs with large rank numbers

We will first characterize graphs with rank number $n-1$, where $n$ is the order of the graph. In this section, we use the notation $H\subseteq G$ to mean that $H$ is a subgraph of $G$.

Lemma 3.1

Let $G$ be a graph of order $n$, and let $G_1$ be a subgraph of $G$ such that $\left|V\left(G_1\right)\right|=n_1$. If ${\chi }_r\left(G_1\right)\le r$ then${\chi }_r\left(G\right)\le r+(n-n_1)$.

Proof

Let $f$ be a ranking of $G_1$ such that $\left|f\right|=r$. Now extend $f$ to a ranking of $G$ by assigning distinct labels from the set $\{r+1,r+2,\dots ,r+(n-n_1)\}$ to vertices in $V\left(G\right)-V\left(G_1\right)$.□

Theorem 3.2

${\chi }_r(K_n-G)=n-1$ if and only if $K_n-G\ne K_n$,$K_3⁄\subseteq G$, and$C_4⁄\subseteq G$.

Proof

Let $K_n-G\ne K_n$, $K_3⁄\subseteq G$, and $C_4⁄\subseteq G$. Since $K_n-G\ne K_n$, ${\chi }_r(K_n-G)\le n-1$.

Consider a ranking $f$ of $K_n-G$. Suppose there exist vertices $a_1,a_2,a_3\in V(K_n-G)$ such that $f\left(a_1\right)=f\left(a_2\right)=f\left(a_3\right)=a$. Then $\{a_1,a_2,a_3\}$ is an independent set in $K_n-G$, and hence form a $K_3$ in $G$, which is a contradiction. Therefore, no label can appear three times or more under $f$.

Now, suppose there are vertices $a_1,a_2,b_1,b_2$ such that $f\left(a_1\right)=f\left(a_2\right)=a$ and $f\left(b_1\right)=f\left(b_2\right)=b$, and without loss of generality, assume that $a>b$. Then $a_1{a}_2\in E\left(G\right)$ and $b_1{b}_2\in E\left(G\right)$ since $f$ is a ranking of $K_n-G$. Moreover, since $K_3⁄\subseteq G$ and $C_4⁄\subseteq G$, there exists at most one edge in $G$ that has endpoints $a_1$ or $a_2$ and $b_1$ or $b_2$. This implies that in $K_n-G$ either $a_1{b}_1{a}_2$ or $a_1{b}_2{a}_2$ is a path that violates the requirements of a ranking, a contradiction. Therefore two labels cannot appear more than once under $f$. Since no label can be used three times and two labels cannot be used more than once, ${\chi }_r(K_n-G)\ge n-1$. Therefore, ${\chi }_r(K_n-G)=n-1$.

Now, suppose ${\chi }_r(K_n-G)=n-1$. Then $K_n-G\ne K_n$ as ${\chi }_r\left(K_n\right)=n$. If $v_1,v_2$, and $v_3$ form $K_3$ in $G$, then $\{v_1,v_2$, $v_3\}$ form an independent set in $K_n-G$ and thus, by Lemma 1.4, ${\chi }_r(K_n-G)\le n-2$, a contradiction. Lastly, assume that $C_4\subseteq G$. We know that ${\chi }_r\left(\overline{C_4}\right)=2$, and thus, by Lemma 3.1, ${\chi }_r(K_n-G)\le n-2$, a contradiction.□

From Theorem 3.2 we get the following corollaries.

Corollary 3.3

${\chi }_r\left(G\right)=n-1$ if and only if $G\ne K_n$,$K_3⁄\subseteq \overline{G}$, and$C_4⁄\subseteq \overline{G}$.

Corollary 3.4

For a tree $T$ on $n>1$ vertices,${\chi }_r\left(\overline{T}\right)=n-1$.

We now look at the characteristics of graphs with rank number $n-2$, where $n$ is the order of the graph. Let $B=W_5-uv$, where $W_5$ is a wheel on $5$ vertices with center vertex $u$ and $v\ne u$ is a vertex in $W_5$. Note that $\overline{B}$ has two components, a $P_3$ and a $P_2$ and hence we have the following observation.

Observation 3.5

${\chi }_r\left(\overline{B}\right)=2$.

Since the graph $\overline{K_{3,3}}$ has two $K_3$ as components, we have the following observation.

Observation 3.6

${\chi }_r\left(\overline{K_{3,3}}\right)=3$.

Theorem 3.7

${\chi }_r(K_n-G)=n-2$ if and only if $K_3\subseteq G$ or $C_4\subseteq G$,$K_4⁄\subseteq G$,$B⁄\subseteq G$ and$K_{3,3}⁄\subseteq G$.

Proof

Suppose that ${\chi }_r(K_n-G)=n-2$. If $K_3⁄\subseteq G$ and $C_4⁄\subseteq G$, then either ${\chi }_r(K_n-G)=n$ or, by Theorem 3.2, ${\chi }_r(K_n-G)=n-1$. If $K_4\subseteq G$, then $K_n-G$ contains an independent set of size $4$, and thus, by Lemma 1.4, ${\chi }_r(K_n-G)\le n-3$. If either $B\subseteq G$ or $K_{3,3}\subseteq G$, then by Observations 3.5 and 3.6 and by Lemma 3.1, we get ${\chi }_r(K_n-G)\le n-3$. Thus if ${\chi }_r(K_n-G)=n-2$ then $K_3\subseteq G$ or $C_4\subseteq G$, $K_4⁄\subseteq G$, $B⁄\subseteq G$ and $K_{3,3}⁄\subseteq G$.

Let $K_3\subseteq G$ or $C_4\subseteq G$, $K_4⁄\subseteq G$, $B⁄\subseteq G$ and $K_{3,3}⁄\subseteq G$. Since $K_3\subseteq G$, or $C_4\subseteq G$, as discussed in the proof of Theorem 3.2, we can find a ranking $f$ of $K_n-G$ with $\left|f\right|\le n-2$. Thus ${\chi }_r(K_n-G)\le n-2$.

Suppose that ${\chi }_r(K_n-G)\le n-3$. Let $f$ be an optimal ranking of $K_n-G$. Then, since $\left|f\right|\le n-3$, one of the following three cases must occur.

Case 1: There exist vertices $v_1,v_2,v_3,v_4\in V(K_n-G)$ such that $f\left(v_1\right)=f\left(v_2\right)=f\left(v_3\right)=f\left(v_4\right)=1$. This means that these vertices form a $K_4$ in $G$, a contradiction.

Case 2: There exist vertices $x_1,x_2,x_3,y_1,y_2\in V(K_n-G)$ such that $f\left(x_1\right)=f\left(x_2\right)=f\left(x_3\right)=1$ and $f\left(y_1\right)=f\left(y_2\right)=2$. Then the vertices $x_1,x_2,x_3$ must form a $K_3$ in $G$ and the vertices $y_1,y_2$ must be adjacent in $G$. Also, each of $x_1,x_2,x_3$ must be adjacent to either $y_1$ or $y_2$ in $G$. (If $x_i$ were adjacent to neither $y_1$ nor $y_2$ for some $1\le i\le 3$ then the path $y_1{x}_i{y}_2$ would exist in $K_n-G$, making $f$ not a ranking.) If each of the $x_i$’s is adjacent to the same $y_j$ for some $1\le j\le 2$ then $x_1,x_2,x_3$, and $y_j$ form a $K_4$ in $G$. If, without loss of generality, $x_1{y}_1\notin E\left(G\right)$, $x_1{y}_2\in E\left(G\right)$, $x_2{y}_1\in E\left(G\right)$, and $x_3{y}_1\in E\left(G\right)$, then the subgraph of $G$ induced by $x_1,x_2,x_3,y_1$, and $y_2$ contains a $B$ with $x_2$ as the center vertex. However, we assumed that $K_4⁄\subseteq G$ and $B⁄\subseteq G$.

Case 3: There exist vertices $x_1,x_2,y_1,y_2,z_1,z_2\in V(K_n-G)$ such that $f\left(x_1\right)=f\left(x_2\right)=1$, $f\left(y_1\right)=f\left(y_2\right)=2$, and $f\left(z_1\right)=f\left(z_2\right)=3$. Then $\{x_1{x}_2,y_1{y}_2,z_1{z}_2\}\in E\left(G\right)$. Let $V_1=\{x_1,x_2\}$, $V_2=\{y_1,y_2\}$, and $V_3=\{z_1,z_2\}$. Since $f$ is a ranking, paths such as $y_1{x}_1{y}_2$ or $z_1{x}_1{z}_2$, or $z_1{y}_1{z}_2$ do not exist in $K_n-G$, and thus in $G$ there must be at least two edges between every $V_i$ and $V_j$, for all $1\le i<j\le 3$. 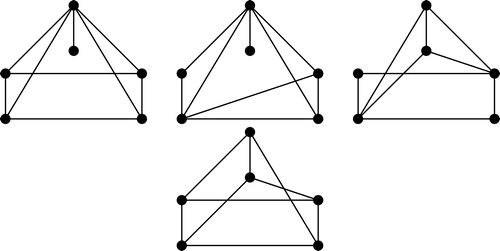Moreover, the subgraph of $K_n-G$ induced by $\{x_1,x_2,y_1,y_2,z_1,z_2\}$ must be disconnected, since the highest label $3$ is used twice in the subgraph. This means $\overline{J}$ is disconnected, where $J$ is the subgraph of $G$ induced by $\{x_1,x_2,y_1,y_2,z_1,z_2\}$. Thus $J$ must contain one of the four graphs on six vertices given in Fig. 7.

Note that the first three graphs contain $B$ as a subgraph, and the last graph is a $K_{3,3}$. This is a contradiction, as we assumed that $B⁄\subseteq G$ and $K_{3,3}⁄\subseteq G$.

Therefore, ${\chi }_r(K_n-G)\ge n-2$, and thus ${\chi }_r(K_n-G)=n-2$.□

Fig. 7 $J$ must contain one of these four graphs.

Corollary 3.8

${\chi }_r\left(G\right)=n-2$ if and only if $K_3\subseteq \overline{G}$ or $C_4\subseteq \overline{G}$,$K_4⁄\subseteq \overline{G}$,$B⁄\subseteq \overline{G}$ and$K_{3,3}⁄\subseteq \overline{G}$.

4 Conclusion

Finding the rank number of a general graph is known to be extremely difficult. In this paper, we identified graphs with rank numbers $n-1$ and $n-2$, where $n$ is the order of the graph. The idea we used for finding ${\chi }_r(K_n-G)$ would still work for classifying graphs with smaller rank numbers. However, the number of labeling schemes that needs to be considered grows exponentially as the rank number decreases. Each of the labeling scheme produces multiple forbidden subgraphs, and hence this method, while not incorrect, will not be feasible for classifying graphs with smaller rank numbers. An interesting related question would be to identify the minimum number of edges required in an $n$ vertex graph $G$ such that rank number of $G$ is either $n-1$ or $n-2$. We also characterized subdivided stars based on their rank numbers, thus establishing the rank number of all subdivided stars. Rankings of some other classes of trees have also been studied by others, for example see [7,10,14], however, the rank number of an arbitrary tree has not been established.