On group vertex magic graphs

Abstract

Let $G=(V\left(G\right),E\left(G\right))$ be a simple undirected graph and let $\mathcal{A}$ be an additive abelian group with identity 0. A mapping $l:V\left(G\right)\to \mathcal{A}\setminus \left\{0\right\}$ is said to be a $\mathcal{A}$-vertex magic labeling of $G$ if there exists an element $\mu$ of $\mathcal{A}$ such that $w\left(v\right)={\sum }_{u\in N\left(v\right)}l\left(u\right)=\mu$ for any vertex $v$ of $G$, where $N\left(v\right)$ is the open neighborhood of $v.$ A graph $G$ that admits such a labeling is called an $\mathcal{A}$-vertex magic graph. If $G$ is $\mathcal{A}$-vertex magic graph for any nontrivial abelian group $\mathcal{A}$, then $G$ is called a group vertex magic graph. In this paper, we obtain a few necessary conditions for a graph to be group vertex magic. Further, when $\mathcal{A}\cong {\mathbb{Z}}_2\oplus {\mathbb{Z}}_2$, we give a characterization of trees with diameter at most 4 which are $\mathcal{A}$-vertex magic.

Keywords:

• $\mathcal{A}$-vertex magic
• Group vertex magic graph
• Weight of a vertex
• Tree

1 Introduction

By a graph $G=(V,E)$ we mean a finite undirected graph with neither loops nor multiple edges. The order $\left|V\right|$ and the size $\left|E\right|$ are denoted by $n$ and $m$ respectively. For graph-theoretic terminology, we refer to Bondy and Murthy [1]. For concepts in group theory, we refer to Herstein [2].

Throughout this paper $\mathcal{A}$ stands for an abelian group with identity element 0. The group ${\mathbb{Z}}_2\oplus {\mathbb{Z}}_2=\{(0,0),(1,0),(0,1),(1,1)\}$ under component-wise addition modulo $2$ is the Klein’s-4 group and is denoted by $V_4$.

Lee et al. [3] introduced the following concept of group-magic graphs.

Definition 1.1

For any abelian group $\mathcal{A}$, a graph $G=(V,E)$ is said to be $\mathcal{A}$-magic if there exists a labeling $l:E\left(G\right)\to A\setminus \left\{0\right\}$ such that the induced vertex labeling $l^{+}:V\left(G\right)\to A$ defined by, $$l^{+}\left(v\right)=\sum _{uv\in E\left(G\right)}l\left(uv\right)$$is a constant map.

Lee et al. [4] obtained a characterization of $V_4$-magic trees.

Theorem 1.2

[4] A tree $T$ is ${\mathbb{Z}}_2\oplus {\mathbb{Z}}_2$-magic if and only if all its vertices have odd degrees.

Low et al. [5] proved the following theorem on $\mathcal{A}$-magic labeling of Cartesian product of two graphs.

Theorem 1.3

[5] Let $\mathcal{A}$ be an abelian group. If $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ are$\mathcal{A}$-magic graphs, then the Cartesian product $G_1\square G_2$ is $\mathcal{A}$-magic.

Further results on group-magic labeling are given in [4–8].

In this paper, we introduce the concept of group vertex magic graphs and present several results on the existence of such labelings for trees with diameter at most 4 and complete multipartite graphs.

2 Main results

Definition 2.1

A mapping $l:V\left(G\right)\to \mathcal{A}\setminus \left\{0\right\}$ is said to be a $\mathcal{A}$-vertex magic labeling of $G$ if there exists an element $\mu$ of $\mathcal{A}$ such that $w\left(v\right)={\sum }_{u\in N\left(v\right)}l\left(u\right)=\mu$ for any vertex $v$ of $G$. A graph $G$ that admits such a labeling is called an $\mathcal{A}$-vertex magic graph. If $G$ is $\mathcal{A}$-vertex magic graph for any nontrivial abelian group $\mathcal{A}$, then $G$ is called a group vertex magic graph.

The following are a few simple observations.

Observation 2.2

If $G$ is a graph having a subgraph $P_4=(u_1,u_2,u_3,u_4)$ such that $deg\left(u_1\right)=1$ and $deg\left(u_3\right)=2$, then$G$ is not$\mathcal{A}$-vertex magic for any abelian group $\mathcal{A}$. In fact if $\ell$ is a$\mathcal{A}$-vertex magic labeling of $G$, then $\ell \left(u_2\right)=w\left(u_1\right)=w\left(u_3\right)=\ell \left(u_2\right)+\ell \left(u_4\right)$. Hence $\ell \left(u_4\right)=0$, which is a contradiction.

Observation 2.3

If $G$ is a graph with two vertices $u$ and $v$ such that $|N\left(u\right)\cap N\left(v\right)|=deg\left(u\right)-1=deg\left(v\right)$, then$G$ is not group vertex magic. Since $|N\left(u\right)\cap N\left(v\right)|=deg\left(u\right)-1=deg\left(v\right)$, there exists a unique vertex $w$ such that $w\in N\left(u\right)$ and $w\notin N\left(v\right)$. Now if $G$ is$\mathcal{A}$-vertex magic for an abelian group $\mathcal{A}$, then $\ell \left(w\right)=0$, which is a contradiction. Hence $G$ is not group vertex magic.

Observation 2.4

If $\mathcal{A}$ is any abelian group of even order, then any graph $G$ with either all vertices are of even degree, or all vertices are of odd degree is$\mathcal{A}$-vertex magic. The group$\mathcal{A}$ has a nonzero element$g$ of order 2, and by labeling all the vertices of $G$ with $g$, we get an$\mathcal{A}$-magic labeling with magic constant zero or $g$ according as the degree of vertices is even or odd.

Observation 2.5

Any $r$-regular graph$G$ is group vertex magic. If we label all the vertices of $G$ with a nonzero element $g$ of$\mathcal{A}$, we get the required labeling with magic constant $rg$.

Theorem 2.6

Let $\mathcal{A}$ be any abelian group with $\left|\mathcal{A}\right|\ge 2$. Then the complete bipartite graph $K_{m,n}$ where $m,n\ge 2$ is$\mathcal{A}$-vertex magic.

Proof

Let $V_1=\{u_1,u_2,\dots ,u_n\}$ and $V_2=\{v_1,v_2,\dots ,v_m\}$ be the bipartition of $K_{m,n}$. Assign labels $\ell \left(u_i\right)$ and $\ell \left(v_j\right)$ where $1\le i\le n-1$ and $1\le j\le m-1$ arbitrarily by the elements of $\mathcal{A}$ such that ${\sum }_{i=1}^{n-1}\ell \left(u_i\right)=a,{\sum }_{j=1}^{m-1}\ell \left(v_j\right)=b$ and $a,b\in \mathcal{A}-\left\{0\right\}$. Now define $\ell \left(u_n\right)=-a$ and $\ell \left(v_m\right)=-b$. This gives an $\mathcal{A}$-vertex magic labeling of $K_{m,n}$ with magic constant 0. □

Theorem 2.7

Let $G=K_{m_1,m_2,\dots ,m_k}$ be a$k$-partite graph. Let$\mathcal{A}$ be an abelian group having at least one element a such that $o\left(a\right)>\ell cm\{m_1,m_2,\dots ,m_k\}$. Then $G$ is$\mathcal{A}$-vertex magic.

Proof

Let $m=\ell cm\{m_1,m_2,\dots ,m_k\}$. Let $V_1,V_2,\dots ,V_k$ be the partite sets of $G$ with $\left|V_i\right|=m_i$. Define $\ell :V\to \mathcal{A}$ by $\ell \left(v\right)=\frac{m}{m_i}a$ for all $v\in V_i$. Clearly $\ell$ is an $\mathcal{A}$-vertex magic labeling of $G$ with magic constant $(k-1)ma$. □

We now proceed to investigate the existence of group magic labelings for trees.

Lemma 2.8

If $n\ge 2$, then any element of $V_4$ can be expressed as ${\sum }_{i=1}^n{g}_i$, where all $g_i$’s are nonzero elements of $V_4$.

Proof

Let $V_4=\{0,a,b,c\}$ where $2a=2b=2c=0$ and sum of any two nonzero elements is the third nonzero element. Hence the result follows trivially when $n=2$. Now let $n>2$ and let $\mu \in V_4$.

We consider two cases.

Case i. $n$ is even.

If $\mu =0$, then $\mu ={\sum }_{i=1}^n{g}_i$, where $g_i=a$ for all $i$.

If $\mu =a$, then $\mu ={\sum }_{i=1}^n{g}_i$, where $g_i=a$ for all $i$ with $1\le i\le n-2$, $g_{n-1}=b$ and $g_n=c$.

The proof is similar if $\mu =b$ or $c$.

Case ii. $n$ is odd.

If $\mu =0$, then $\mu ={\sum }_{i=1}^n{g}_i$, where $g_1=a,g_2=b$ and $g_i=c$ for all $i,3\le i\le n$.

If $\mu =a$, then $\mu ={\sum }_{i=1}^n{g}_i$, where $g_i=b$ if $1\le i\le n-1$ and $g_n=a$.

The proof is similar for $\mu =b$ or $c$. □

We now proceed to consider the existence of group vertex magic labelings for trees with diameter 2.

Theorem 2.9

Let $T$ be a tree of order $n$ and diameter 2.

(i)	The tree $T$ is $V_4$-vertex magic.
(ii)	If $n$ is even, then $T$ is group vertex magic.

Proof

(i) Since the diameter of $T$ is 2, $T=K_{1,n-1}$ where $n\ge 3$. Let $v_0$ be the center of $T$ and let $v_1,v_2,\dots ,v_{n-1}$ be the leaves of $T$.

By Lemma 2.8, the element $a$ in $V_4$ can be written as $a={\sum }_{i=1}^{n-1}{g}_i$ where $g_i$ are nonzero elements of $V_4$.

Now define $\ell$ by $\ell \left(v_i\right)=\left\{\begin{array}{cc}a\hfill & \text{if}i=0\hfill \\ g_i\hfill & \text{if}1\le i\le n-1.\hfill \end{array}\right.$

Clearly $\ell$ is a $V_4$-vertex magic labeling of $T$ with magic constant $a$.

(ii) Suppose $n$ is even. Let $\mathcal{A}$ be any abelian group of order $m$. Let $g\in \mathcal{A}$.

Define $\ell :V\to \mathcal{A}$ by $$\ell \left(v\right)=\left\{\begin{array}{cc}g\hfill & \text{if}v=v_0\text{or}{v}_{n-1}\hfill \\ -g\hfill & \text{if}v=v_i,i\text{is even and}i\ne 0,n-1\hfill \\ g\hfill & \text{if}v=v_i\text{and}i\text{is odd.}\hfill \end{array}\right.$$Clearly $\ell$ is a group-vertex magic labeling of $K_{1,n}$ with magic constant $g$. □

Observation 2.10

Let $\mathcal{A}$ be an abelian group with $\left|\mathcal{A}\right|>2$. The path $P_2$ is trivially$\mathcal{A}$-vertex magic. It follows from Theorem 2.9 that $P_3$ is $\mathcal{A}$-vertex magic.

We now proceed to characterize $V_4$-vertex magic trees of diameter 3.

Let $T$ be a tree with diameter 3. Then $T$ is isomorphic to the bistar $B(r,s)$, $V\left(B_{r,s}\right)=\{v_1,v_2,u_1,u_2,\dots ,u_r,w_1,w_2,\dots ,w_s\},u_1,u_2,\dots ,u_r$ are pendant vertices adjacent to $v_1$ and $w_1,w_2,\dots ,w_s$ are pendant vertices adjacent to $v_2$.

The graph $B_{r,s}$ is given in Fig. 1.

Fig. 1 A tree with diameter 3.

Theorem 2.11

Let $T=B_{r,s}$ be a tree with diameter 3. Then $T$ is $V_4$-vertex magic if and only if $r\ge 2$ and $s\ge 2$.

Proof

If $r=1$ or $s=1$, then it follows from Observation 2.3 that $T$ is not $V_4$-vertex magic. Now, let $r\ge 2$ and $s\ge 2$. It follows from Lemma 2.8 that the element $0$ in $V_4$ can be written as $0={\sum }_{i=1}^r{g}_i={\sum }_{i=1}^s{h}_i$ where $g_i$ and $h_j$ are nonzero elements of $V_4$.

Now define $\ell :V\left(T\right)\to V_4$ by

$\ell \left(v_1\right)=\ell \left(v_2\right)=a,\ell \left(u_i\right)=g_i$ and $\ell \left(v_j\right)=h_j$. Clearly $\ell$ is a $V_4$-vertex magic labeling of $T$ with magic constant $a$. □

Corollary 2.12

Any $V_4$-vertex magic tree $T$ of diameter 3 has a $V_4$-vertex magic subtree of diameter 2.

Proof

The subtree $T$ obtained from $T$ by deleting all the pendant vertices adjacent to a central vertex is a $V_4$-vertex magic tree of diameter 2. □

Theorem 2.13

A tree with diameter 4 is $V_4$ vertex magic if and only if either of the following holds.

(i)	Each internal vertex has at least two neighbors which are pendant vertices.
(ii)	Central vertex has an odd degree without any pendant vertex as its neighbor.
(iii)	Central vertex has an odd degree with exactly one pendant vertex as its neighbor, and all other internal vertices have at least two pendant vertices as its neighbor.

Proof

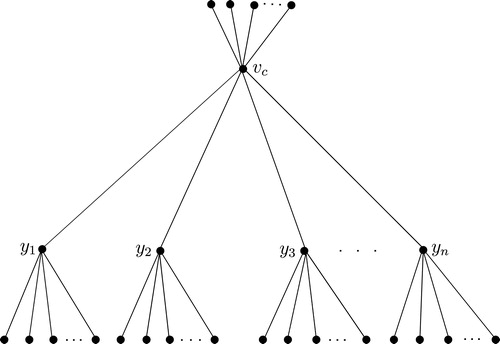
A tree $T$ of diameter 4 is of the form given in Fig. 2. Note that $v_c$ is the central vertex of $T$. Let $N_{ext}\left(v_c\right)=\{v\in V:v\in N\left(v_c\right)$ and $deg\left(v\right)=1\}$ and $N_{int}\left(v_c\right)=\{v\in V:v\in N\left(v_c\right)$ and $deg\left(v\right)>1\}$. Clearly $deg\left(v_c\right)=\left|N_{int}\left(v_c\right)\right|+\left|N_{ext}\left(v_c\right)\right|$. Now, suppose $T$ is $V_4$-vertex magic with labeling $\ell$. Let $y_i\in N_{int}\left(v_c\right)$ and $\ell \left(y_i\right)=g$ where $g\in V_4\setminus \left\{0\right\}$. Hence it follows that $w\left(v\right)=g$ for all $v\in V\left(T\right)$. Therefore, $\ell \left(y_i\right)=g$ for all $y_i\in N_{int}\left(v_c\right)$.

Suppose (i) is not true.

Then we have the following cases.

Case 1. $v_c$ has at least one pendant vertex as its neighbor.

In this case each $y_i$ has at least two pendant vertices as its neighbor. Hence $v_c$ has exactly one pendant vertex as its neighbor, say $w$. Suppose $deg\left(v_c\right)$ is even. Since $w\left(v\right)=g$ for all $v\in V\left(T\right)$, we have $w\left(v_c\right)=l\left(w\right)+g=g$. Hence $l\left(w\right)=0$, which is a contradiction.

Case 2. $v_c$ does not have a pendant vertex as its neighbor.

If $deg\left(v_c\right)$ is even, then $w\left(v_c\right)=0$, which is a contradiction. Hence $deg\left(v_c\right)$ is odd.

We now proceed to prove the converse.

Suppose all the internal vertices of $T$ have at least two neighbors which are pendant vertices. Let $\ell \left(v\right)=g$ for all internal vertices, so that $w\left(v\right)=g$ for all pendant vertices $u$. It follows from Lemma 2.8 that all the pendant vertices of $T$ can be labeled in such a way that $w\left(v\right)=g$ for all internal vertices. This gives a $V_4$-vertex magic labeling of $T$.

Now suppose $deg\left(v_c\right)$ is odd with at most one pendant vertex as its neighbor. If $\left|N_{ext}\left(v_c\right)\right|=0$, define $\ell \left(y_i\right)=g$ for all $y_i\in N_{int}\left(v_c\right)$. Since $deg\left(v_c\right)$ is odd, $w\left(v_c\right)=g$. Now it follows from Lemma 2.8 that all the pendant vertices of $T$ can be labeled in such a way that $w\left(y_i\right)=g$ for all $y_i\in N_{int}\left(v_c\right)$. This gives a $V_4$-vertex magic labeling of $T$.

Further, when $\left|N_{ext}\left(v_c\right)\right|=1$ and each $y_i$ has at least two pendant vertices as its neighbor. Then $\left|N_{int}\left(v_c\right)\right|$ is even. Let $N_{ext}\left(v_c\right)=\left\{w\right\}$. Define $\ell \left(w\right)=g,\ell \left(v_c\right)=g$ and $\ell \left(y_i\right)=g$ for all $y_i\in N_{int}\left(v_c\right)$. Since $deg\left(v_c\right)$ is odd, $w\left(v_c\right)=deg\left(v_c\right)g=g$. It follows from Lemma 2.8 that all the remaining pendant vertices of $T$ can be labeled in such a way that $w\left(y_i\right)=g$ for all $y_i\in N_{int}\left(v_c\right)$. This gives a $V_4$-vertex magic labeling of $T$. □

Fig. 2 Diameter 4 tree.

3 Conclusion and scope

In this paper, we have introduced the concept of group vertex magic labeling and investigated the existence of such labelings for trees of diameter at most 4, when the group is the Klein’s-4 group. The investigation of the existence of such a labeling for arbitrary abelian groups and for other families of graphs are directions for further research.