A closed -knight’s tour on some cylinder chessboards

Abstract

A $(2,3)$-knight’s move on the $m\times n$ cylinder chessboard is the move of the knight 2 squares vertically or 2 squares horizontally and then 3 squares perpendicular to it. In this paper, we show a closed $(2,3)$-knight’s tour on the $5k\times n$ cylinder chessboard for all positive integers $k$ and $n$, and a closed $(2,3)$-knight’s tour on the $9k\times n$ cylinder chessboard for all positive integers $k$ and $n\in \{4,5,7,8,9,10,11,12,13\}$. Moreover, we show that there is no closed $(2,3)$-knight’s tours on the $m\times n$ cylinder chessboard where (i) $m\in \{1,2,3,4,6,7,8\}$ and (ii) $m=9$ and $n\in \{1,2,3,6\}$.

Keywords:

• Closed $(a,b)$-knight’s tour
• Cylinder chessboard
• Hamiltonian cycle

1 Introduction and preliminaries

The $m\times n$ chessboard is an array with $m$ rows and $n$ columns. A legal knight’s move is the moves from one square vertically or one square horizontally and then two squares perpendicular to it. A question of the $m\times n$ chessboard is “which chessboard that the knight can move to all squares of the chessboard exactly once and return to the starting square?” The knight’s moves that move to all squares of the chessboard exactly once and return to the starting square is called a closed knight’s tour. The answer of this question was obtained by Schwenk [1] in 1991 as follows.

Theorem 1

[1] The $m\times n$ chessboard with $m\le n$ admits a closed knight’s tour unless one or more of the following conditions hold :

(i) $m$ and $n$ are both odd;

(ii) $m=1,2$ , or $4$ ; or

(iii) $m=3$ and $n=4,6$ or $8$ .

In 2005, Chia et al. [2] generalized the legal knight’s move to an $(a,b)$-knight’s move. That is, the knight can move $a$ squares vertically or $a$ squares horizontally and then $b$ squares perpendicular to it. Then, the legal knight’s move is a $(1,2)$-knight’s move. The problem is similar to the legal knight’s move. The $(a,b)$-knight’s moves that move to all squares of the chessboard exactly once and return to the starting square is called a closed $(a,b)$ -knight’s tour. The authors in [2] obtained the following result for the $(2,3)$-knight’s move.

Theorem 2

[2] The $5k\times n$ chessboard where $(5k,n)\ne (5,18)$ admits a closed $(2,3)$ -knight’s tour if and only if

(i)	$k=1$ and $n\ge 16$ is even; or
(ii)	$k=2$ and $n\ge 10$ and $n\ne 12$ ; or
(iii)	$k\ge 3$ is odd and $n\ge 10$ is even and $n\ne 12$ ; or
(iv)	$k\ge 4$ is even and $n=5,9,10,11$ or $n\ge 13$ .

The knight’s tour problem was discussed in the $m\times n$ cylinder chessboard. We can think of creating the $m\times n$ cylinder chessboard by starting with an $m\times n$ chessboard and then joining the left end with the right end. In [3], Watkins obtained the following result.

Theorem 3

[3] An $m\times n$ cylinder chessboard has a closed knight’s tour unless one of the following two conditions holds: (a) $m=1$ and $n>1$ ; or (b) $m=2$ or $4$ and $n$ is even.

In this paper, we consider a $(2,3)$-knight’s move on the cylinder chessboard. A closed $(2,3)$-knight’s tour on the $5k\times n$ cylinder chessboard for all positive integers $k$ and $n$, and a closed $(2,3)$-knight’s tour on the $9k\times n$ cylinder chessboard for all positive integers $k$ and $n\in \{4,5,7,8,9,10,11,12,13\}$ are shown in Theorems 6 and 8, respectively. Moreover, we show that the $m\times n$ cylinder chessboard, where $m\in \{1,2,3,4,6,7,8\}$ contains no closed $(2,3)$-knight’s tours (in Theorem 5) and the $9\times n$ cylinder chessboard, where $n\in \{1,2,3,6\}$, also contains no closed $(2,3)$-knight’s tours (in Lemma 2).

2 Main results

For an $m\times n$ cylinder chessboard, we start with an $m\times n$ chessboard. When we consider the $m\times n$ cylinder chessboard with an $m\times n$ chessboard, let each square be $(i,j)$ where $(i,j)$ is counting in the matrix fashion. If the knight stands at $(i,j)$, then the knight can move to at most eight squares : $(i\pm 2,j\pm 3)$ and $(i\pm 3,j\pm 2)$ where $j\pm 3$ and $j\pm 2$ are in modulo $n$.

The knight’s tour problem can be considered by using a graph. Let $G$ be a graph with $V\left(G\right)=\left\{(i,j)\right|i\in \{1,2,3,\dots ,m\}\text{and}j\in \{1,2,3,\dots ,n\}\}$. Two vertices, $(i,j)$ and $(k,l)$, are adjacent if the knight can move from $(i,j)$ to $(k,l)$. Then, a closed $(2,3)$-knight’s tour is a Hamiltonian cycle of a graph $G$, a cycle of $G$ that contains all vertices of $G$.

Before proving the main results, we need the following well-known result concerning Hamiltonian cycle (see for example [4]).

Theorem 4

Let $S$ be a proper subset of the vertex set of a graph $G$ . If $G$ contains a Hamiltonian cycle, then $G-S$ contains at most $\left|S\right|$ components.

If $G$ is a graph and $A$ is a subset of $V\left(G\right)$, let $G\left[A\right]$ denote a subgraph of $G$ induced by $A$.

Theorem 5

Suppose that $m\le 8$ and $m\ne 5$ . Then, the $m\times n$ cylinder chessboard contains no closed $(2,3)$ -knight’s tours for any positive integer $n$ .

Proof

Let $G$ be a graph representing the $m\times n$ cylinder chessboard.

Case 1: $m\in \{1,2,3,4\}$. If $m\in \{1,2,3\}$, then $G$ is a disconnected graph. Thus, it has no closed $(2,3)$-knight’s tours. Next, let $m=4$.

If $n=1,2,3$ or $n=6$, then the degree of vertices $(2,1)$ is $1$. Then, $G$ contains no Hamiltonian cycle.

If $n\ge 4$ and $n\ne 6$, then we consider vertices in the 2nd row. Since, for $j\in \{1,2,3,\dots ,n\}$, vertex $(2,j)$ in the 2nd row is adjacent to vertices $(4,t_1)$ and $(4,t_2)$ where $t_1\equiv j+3$ (mod $n$) and $t_2\equiv j-3$ (mod $n$), the degree of each vertex in the 2nd row is $2$. If $G$ contains a Hamiltonian cycle, then such two edges that incident with each vertex in the 2nd row must be in the Hamiltonian cycle. We see that edges incident with vertices in the 2nd row form cycle which is not a Hamiltonian cycle. The cycle starts at $(2,1)$, goes on the right side of the chessboard and then returns to the left side of the chessboard until we end at the right side.

Case (i): $n\equiv 0$ (mod $3$). Let $n=3t$ for some positive integer $t\ge 3$. The cycle is in the following form.

$(2,1),(4,4),(2,7),(4,10),(2,13),(4,16),\dots ,(4,3t-5),(2,3t-2)$,

$(4,1),(2,4),(4,7),(2,10),(4,13),(2,16),\dots ,(2,3t-5),(4,3t-2),(2,1)$.

Case (ii): $n\equiv 1$ (mod $3$). Let $n=3t+1$ for some positive integer $t$. The cycle is in the following form.

$(2,1),(4,4),(2,7),(4,10),(2,13),(4,16),\dots ,(2,3t-2),(4,3t+1)$,

$(2,3),(4,6),(2,9),(4,12),(2,15),(4,18),\dots ,(4,3t-3),(2,3t)$,

$(4,2),(2,5),(4,8),(2,11),(4,14),(2,17),\dots ,(2,3t-4),(4,3t-1),(2,1)$.

Case (iii): $n\equiv 2$ (mod $3$). Let $n=3t+2$ for some positive integer $t$. The cycle is in the following form.

$(2,1),(4,4),(2,7),(4,10),(2,13),(4,16),\dots ,(2,3t-2),(4,3t+1)$,

$(2,2),(4,5),(2,8),(4,11),(2,14),(4,17),\dots ,(2,3t-1),(4,3t+2)$,

$(2,3),(4,6),(2,9),(4,12),(2,15),(4,18),\dots ,(4,3t-3),(2,3t)$

$(4,1),(2,4),(4,7),(2,10),(4,13),(2,16),\dots ,(4,3t-2),(2,3t+1)$,

$(4,2),(2,5),(4,8),(2,11),(4,14),(2,17),\dots ,(4,3t-1),(2,3t+2)$,

$(4,3),(2,6),(4,9),(2,12),(4,15),(2,18),\dots ,(2,3t-3),(4,3t),(2,1)$.

Case 2: $m\in \{6,7,8\}$.

Case 2.1: $m=6$. Let $S=\{(3,j),(4,j)|j\in \{1,2,3,\dots ,n\}\}$. Then, $\left|S\right|=2n$.

If $n=1,3$ or $n\ge 5$, let $G_1$ be a subgraph of $G$ induced by the set of vertices $(2,j)$ and $(4,j)$ where $j\in \{1,2,3,\dots ,n\}$. Then, $G-S$ contains $G_1$ and $2n$ isolated vertices from the 1st and 6th rows. By Theorem 4, $G$ contains no Hamiltonian cycles. (See Fig. 1.)

If $n=2$ (respectively $n=4$), then $G-S$ contains $6$ (respectively $12$) components. Fig. 1 shows the graph $G-S$ where the white vertices are in $S$. By Theorem 4, $G$ contains no Hamiltonian cycles.

Case 2.2: $m=7$. Let $S=\{(3,j),(4,j),(5,j)|j\in \{1,2,3,\dots ,n\}\}$. Then, $\left|S\right|=3n$ and $G-S$ contains $4n$ isolated vertices from the $1^{st},2^{nd},6^{th}$ and 7th rows. By Theorem 4, $G$ contains no Hamiltonian cycles.

Case 2.3: $m=8$. Let $S=\{(4,j),(5,j)|j\in \{1,2,3,\dots ,n\}\}$. Then, $\left|S\right|=2n$.

If $n$ is odd, let $G_1$ be a subgraph of $G$ induced by the set of vertices $(1,j),(3,j),(6,j)$ and $(8,j)$ where $j\in \{1,2,3,\dots ,n\}$. Then, $G-S$ contains $G_1$ and $2n$ isolated vertices from the 2nd and 7th rows. By Theorem 4, $G$ contains no Hamiltonian cycles.

If $n$ is even, let $A_1=\{(1,j),(3,j+1),(6,j+1),(8,j)|j\in \{1,3,5,\dots ,n-1\}\}$ and $A_2=\{(1,j),(3,j-1),(6,j-1),(8,j)|j\in \{2,4,6,\dots ,n\}\}$. Then, $G-S$ contains $G\left[A_1\right],G\left[A_2\right]$ and $2n$ isolated vertices from 2nd and 7th rows. By Theorem 4, $G$ contains no Hamiltonian cycles.

This completes the proof. □

Fig. 1 $G-S$ where the white vertices are in $S$.

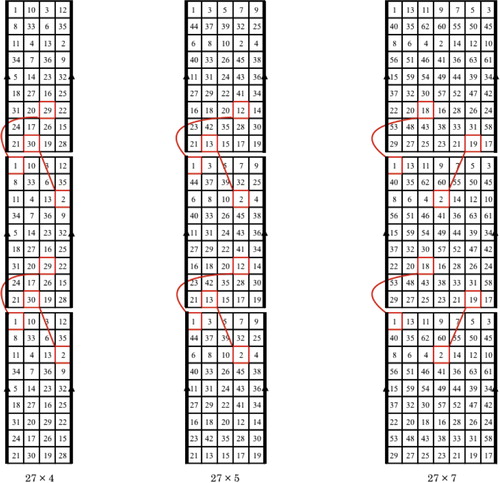
Lemma 1

The $5\times n$ cylinder chessboard admits a closed $(2,3)$ -knight’s tour for any positive integer $n$ .

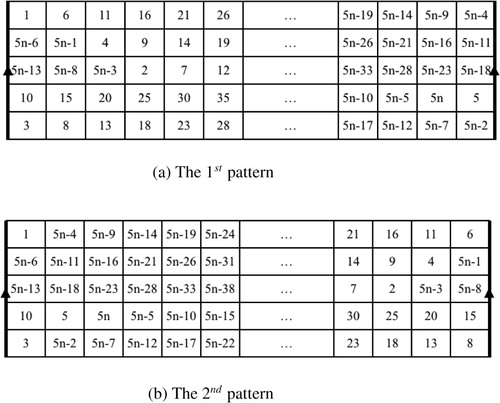
Proof

Let $n$ be a positive integer. We give two patterns to construct a closed $(2,3)$-knight’s tour for the $5\times n$ cylinder chessboard. Since the total number of squares of the $5\times n$ cylinder chessboard is $5n$, for each pattern, we start the first position at $(1,1)$ labeled with number $1$. We define four directions of the knight’s move as follows.

$a$ means the knight moves two squares downward and then goes three squares to the right,

$b$ means the knight moves two squares downward and then goes three squares to the left,

$c$ means the knight moves three squares upward and then goes two squares to the right, and

$d$ means the knight moves three squares upward and then goes two squares to the left.

Then, we obtain two patterns of a closed $(2,3)$-knight’s tour as follows.

For the 1st pattern, the first, second, third, fourth and fifth moves are $a,b,c,b$ and $c$, respectively. We repeat this algorithm for $n$ times (see Fig. 2(a)).

For the 2nd pattern, the first, second, third, fourth and fifth moves are $b,a,d,a$ and $d$, respectively. We repeat this algorithm for $n$ times (see Fig. 2(b)).

We obtain some observations as follows.

(i) For each loop, the starting point is on the 1st row,

(ii) the 1st number of each loop is $5k-4$ where $k\in \{1,2,3,\dots ,n\}$,

(iii) squares labeled with the five consecutive numbers are on different rows, for example, squares labeled with $1,2,3,4$ and $5$ stand in the 1st, 3rd, 5th, 2nd and 4th rows, respectively,

(iv) if $X$ is the first number of a loop and stands at $(1,j)$, then $X+5$ is the first number of the next loop and stands at $(1,j+1)$ if the knight move with the first pattern or at $(1,j-1\text{(mod)}n)$ if the knight move with the second pattern.

By the observation, the 1st number of each loop stands in the different squares. The 2nd, 3rd, 4th and 5th numbers of each loop are considered in similar way. Then, the knight moves to all squares exactly once and the number $5n$ is on $(4,n-1)$ if the knight move with the first pattern, or $(4,3)$ if the knight move with the second pattern. Thus, the knight can move to the first position $(1,1)$. □

Fig. 2 Two patterns of a closed $(2,3)$-knight’s tour on the $5\times n$ cylinder chessboard.

Theorem 6

The $5k\times n$ cylinder chessboard admits a closed $(2,3)$ -knight’s tour for any positive integers $k$ and $n$ .

Proof

If $k=1$, then a closed $(2,3)$-knight’s tour is obtained by Lemma 1. Suppose that $k\ge 2$. The $5k\times n$ cylinder chessboard is obtained from $k$ copies of the $5\times n$ cylinder chessboards by putting each copy from the top to the bottom. We count all copies from the top to the bottom. Since each copy contains a closed $(2,3)$-knight’s tour, we combine each tour of each $5\times n$ cylinder chessboard to a single tour by deleting one edge from the top and the bottom and two edges from the $i$th cylinder chessboard for all $i\in \{2,3,4,\dots ,k-1\}$ and then joining each piece to a single cycle.

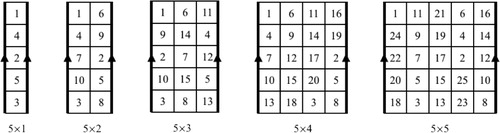
Case 1 : $n\le 5$. We give another pattern for the $5\times n$ cylinder chessboard which is different from the two patterns of Lemma 1 (shown in Fig. 3).

If $n=1$, then delete edge 2–3 of the $i$th copy, and edge 1–2 of $(i+1)$th copy and then join $2$ (respectively $3$) of the $i$th copy to $1$ (respectively $2$) of the $(i+1)$th copy for all $i\in \{1,2,3,\dots ,k-1\}$.

If $n=2,3$ or $4$, then delete edge 2–3 of the $i$th copy, and edge 6-7 of $(i+1)$th copy and then join $2$ (respectively $3$) of the $i$th copy to $6$ (respectively $7$) of the $(i+1)$th copy for all $i\in \{1,2,3,\dots ,k-1\}$.

If $n=5$, then delete edge 2–3 of the $i$th copy, and edge 11–12 of $(i+1)$th copy and then join $2$ (respectively $3$) of the $i$th copy to $11$ (respectively $12$) of the $(i+1)$th copy for all $i\in \{1,2,3,\dots ,k-1\}$.

Case 2 : $n>5$. If $k=2$, the $10\times n$ cylinder chessboard is obtained from $2$ copies of the $5\times n$ cylinder chessboards by putting each copy from the top to the bottom. The top copy is assigned by the 1st pattern of a closed $(2,3)$-knight’s tour and the bottom copy is assigned by the 2nd pattern of a closed $(2,3)$-knight’s tour from Lemma 1. Thus, we combine each tour of each copy to a single tour by deleting edge $(5n-2)-(5n-3)$ from the top and edge $1-2$ from the bottom and then joining $5n-3$ to $1$ and $5n-2$ to $2$.

Next, suppose that $k\ge 3$. The $5k\times n$ cylinder chessboard is obtained from $k$ copies of the $5\times n$ cylinder chessboards by putting each copy from the top to the bottom and counting all copies from the top to the bottom. If $i$ is odd, then the $i$th copy is assigned by the 1st pattern of a closed $(2,3)$-knight’s tour from Lemma 1. If $i$ is even, then the $i$th copy is assigned by the 2nd pattern of a closed $(2,3)$-knight’s tour from Lemma 1. Thus, we combine each tour of each copy to a single tour as follows.

1. Delete edge $(5n-2)-(5n-3)$ from the 1st copy and edge $1-2$ from the $k$th copy.

2. For $i\in \{2,3,4,\dots ,k-1\}$, delete edges $1-2$ and $(5n-2)-(5n-3)$ from the $i$th copy.

3. For $i\in \{2,3,4,\dots ,k-1\}$, join $1$ and $2$ of the $i$th copy to $5n-3$ and $5n-2$ of the $(i-1)$th copy, respectively.

This completes the proof. □

Fig. 3 Closed $(2,3)$-knight’s tours on the $5\times n$ where $n\le 5$.

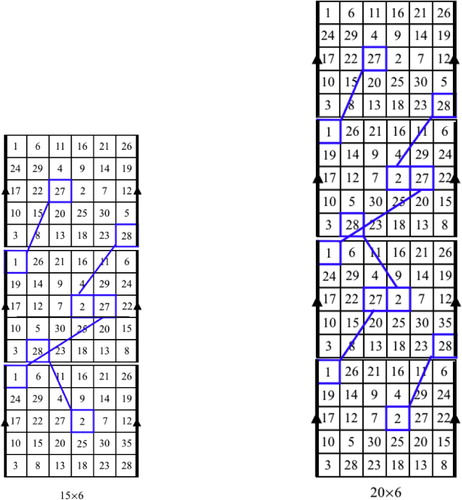
Fig. 4 illustrates closed $(2,3)$-knight’s tours on 15 × 6 and 20 × 6 cylinder chessboards.

Fig. 4 Illustrated closed $(2,3)$-knight’s tours on 15 × 6 and 20 × 6 cylinder chessboards.

For the $9\times n$ cylinder chessboard, we consider $n\le 13$.

Lemma 2

Let $n\in \{1,2,3,6\}$ . Then, the $9\times n$ cylinder chessboard admits no closed $(2,3)$ -knight’s tours.

Proof

Let $n\in \{1,2,3,6\}$ and $G$ be a graph representing the $9\times n$ cylinder chessboard. For $j\in \{1,2,3,\dots ,n\}$, let $B_j=\{(1,j),(3,t)|t\equiv j+3\left(\text{mod}n\right)\}$ and $C_j=\{(7,j),(9,t)|t\equiv j+3\left(\text{mod}n\right)\}$n. Let $S=\{(4,j),(5,j),(6,j)|j\in \{1,2,3,\dots ,n\}\}$. Then, $\left|S\right|=3n$ and $G-S$ contains $2n$ isolated from the 2nd and 8th rows, $G\left[B_j\right]$ and $G\left[C_j\right]$ where $j\in \{1,2,3,\dots ,n\}$. By Theorem 4, $G$ contains no Hamiltonian cycles. □

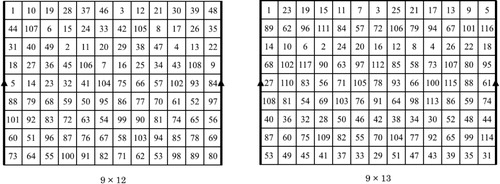
Theorem 7

Let $n$ be an integer such that $n\le 13$ . Then, the $9\times n$ cylinder chessboard admits a closed (2, 3)-knight’s tour if and only if $n\notin \{1,2,3,6\}$ .

Proof

If $n\in \{1,2,3,6\}$, then by Lemma 2, the $9\times n$ cylinder chessboard admits no closed (2, 3)-knight’s tours. Closed (2, 3)-knight’s tours on the $9\times n$ cylinder chessboard where $n\in \{4,5,7,8,9,10,11,12,13\}$ are shown in Figs. 5 and 6. □

Fig. 5 Closed (2, 3)-knight’s tours on the $9\times n$ cylinder chessboard where $n\in \{4,5,7,8,9,10,11\}$.

Fig. 6 Closed (2, 3)-knight’s tours on the $9\times n$ cylinder chessboard where $n\in \{12,13\}$.

Theorem 8

Suppose that $n\le 13$ and $n\notin \{1,2,3,6\}$ . Then, the $9k\times n$ cylinder chessboard admits a closed $(2,3)$ -knight’s tour for any positive integer $k$ .

Proof

If $k=1$, then a closed $(2,3)$-knight’s tour is obtained by Theorem 7. Suppose that $k\ge 2$. The $9k\times n$ cylinder chessboard is obtained from the $k$ copies of $9\times n$ cylinder chessboards by putting each copy from the top to the bottom. We count all copies from the top to the bottom. Since each copy contains a closed $(2,3)$-knight’s tour, we combine each tour of each $9\times n$ cylinder chessboard to a single tour by deleting one edge from the top and the bottom and two edges from the $i$th copy where $i\in \{2,3,4,\dots ,k-1\}$ and then joining each piece to a single cycle.

Case 1: $n=4$. Delete edge 29–30 of the $i$th copy and edge 1–2 of the $(i+1)$th copy and then join $29$ (respectively $30$) of the $i$th copy to $1$ (respectively $2$) of the $(i+1)$th copy for all $i\in \{1,2,3,\dots ,k-1\}$.

Case 2: $n=5$. Delete edge 12–13 of the $i$th copy and edge 1–2 of the $(i+1)$th copy and then join $12$ (respectively $13$) of the $i$th copy to $1$ (respectively $2$) of the $(i+1)$th copy for all $i\in \{1,2,3,\dots ,k-1\}$.

Case 3 : $n\ge 7$. Let $A$ be a number $X$ of $(n-2,3)$. Then, for each $n$, the number $X+1$ or $X-1$ is on $(n,6)$. Assume that $B\in \{X+1,X-1\}$. Delete edge $A-B$ of the $i$th copy and edge 1–2 of the $(i+1)$th copy and then join $A$ (respectively $B$) of the $i$th copy to $1$ (respectively $2$) of the $(i+1)$th copy for all $i\in \{1,2,3,\dots ,k-1\}$. □

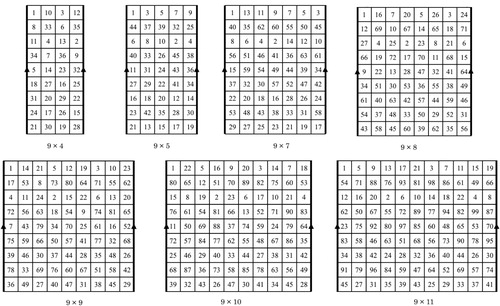
Fig. 7 illustrates closed (2,3)-knight’s tours on the $27\times 4$, $27\times 5$ and $27\times 7$ cylinder chessboards. In future research, we will try to see whether the $9k\times n$ cylinder chessboard has a closed $(2,3)$-knight’s tour or not.

Fig. 7 Illustrated closed (2, 3)-knight’s tours on the $27\times 4,27\times 5$ and 27 × 7 cylinder chessboards.

Acknowledgments

I would like to thank the referees for their comments and suggestions on the manuscript.