A note on comaximal ideal graph of commutative rings

Abstract

Let $R$ be a commutative ring with identity. The comaximal ideal graph $\mathbb{G}\left(R\right)$ of $R$ is a simple graph with its vertices are the proper ideals of R which are not contained in the Jacobson radical of $R$, and two vertices $I_1$ and $I_2$ are adjacent if and only if $I_1+I_2=R$. In this paper, a dominating set of $\mathbb{G}\left(R\right)$ is constructed using elements of the center when $R$ is a commutative Artinian ring. Also we prove that the domination number of $\mathbb{G}\left(R\right)$ is equal to the number of factors in the Artinian decomposition of $R$. Also, we characterize all commutative Artinian rings(non local rings) with identity for which $\mathbb{G}\left(R\right)$ is planar.

Keywords:

• Comaximal ideal graph
• Artinian ring
• Nilpotency
• Domination number
• Planar

1 Introduction

In recent years, the interplay between ring structure and graph structure is studied by many researchers. For such kind of study, researchers define a graph whose vertices are a set of elements in a ring or a set of ideals in a ring and edges are defined with respect to a condition on the elements of the vertex set. A graph is defined out of nonzero zero divisors of a ring and is called zero-divisor graph of a ring [1]. Interesting variations are also defined like comaximal graph [2], total graph [3] and unit graph [4] associated with rings. In ring theory, the structure of a ring $R$ is closely tied to ideal’s behavior more than elements, and so it is deserving to define a graph with vertex set as ideals instead of elements. In view of this, M. Behboodi and Z. Rakeei [5,6] have introduced and investigated a graph called the annihilating-ideal graph of a commutative ring. The annihilating-ideal graph $\mathbb{AG}\left(R\right)$ of $R$ is defined as the graph with the vertex set $\mathbb{A}{\left(R\right)}^{\ast }$ and two distinct vertices $I_1$ and $I_2$ are adjacent if and only if $I_1{I}_2=\left(0\right)$. In 2012, M. Ye and T. Wu defined a new graph structure on commutative rings in [7]. They used ideals instead of elements of a ring, and they named such a graph structure, the comaximal ideal graph. The comaximal ideal graph $\mathbb{G}\left(R\right)$ of $R$ is a simple graph with its vertices the proper ideals of R which are not contained in the Jacobson radical of $R$, and two vertices $I_1$ and $I_2$ are adjacent if and only if $I_1+I_2=R$.

In 2016, Azadi et al. [8] studied the graph structure defined by M. Ye and T. Wu. They investigated the planarity and perfection of comaximal ideal graph. Later, Visweswaran et al. [9] studied the same and independently characterized commutative ring whose comaxial ideal graph is planar. The graphs constructed from rings help us to study the algebraic properties of rings using graph theoretical tools and vice-versa.

Let $G=(V,E)$ be a simple graph. The distance between two vertices $x$ and $y$, denoted $d(x,y)$, is the length of the shortest path from $x$ to $y$. The diameter of a connected graph $G$ is the maximum distance between two distinct vertices of $G$. The eccentricity of $x$, denoted $e\left(x\right)$, is the maximum of the distances from $x$ to the other vertices of $G$. The set of vertices with minimum eccentricity is called the center of the graph $G$, and this minimum eccentricity value is the radius of $G$. The status of $v$ is sum of the distance from $v$ to other vertices of $G$ and is denoted by $s\left(v\right)$. The set of vertices with minimal status is called the median of the graph $G$. For basic definitions on graphs, one may refer [10].

In this paper, we find certain central sets in the comaximal ideal graph and use the same to obtain the value of certain domination parameters of the comaximal ideal graph. Also, we discuss about the planarity condition of the comaximal ideal graph of a commutative ring. The following results are useful for further reference in this paper.

Theorem 1.1

[11, Theorem 8.7] An Artinian ring is uniquely (up to isomorphism) a finite direct product of Artinian local rings.

Theorem 1.2

[7, M. Ye and T. Wu] Let $R$ be a commutative ring. Then $\mathbb{G}\left(R\right)$ is the empty graph if and only if $R$ is a local ring.

Theorem 1.3

[7, M. Ye and T. Wu] Let $R$ be a commutative ring. Then the following statements are equivalent:

$\left(i\right)$ $\mathbb{G}\left(R\right)$ is a complete graph

$\left(ii\right)$ $diam\left(\mathbb{G}\left(R\right)\right)=1$

$\left(iii\right)$ $\mathbb{G}\left(R\right)=K_2$

$\left(iv\right)$ $R=F_1\times F_2$ , where $F_1$ and $F_2$ are fields.

Theorem 1.4

[7, M. Ye and T. Wu] For a ring $R$ , the following statements are equivalent:

$\left(i\right)$ $\mathbb{G}\left(R\right)$ is a complete bipartite graph

$\left(ii\right)$ $\mathbb{G}\left(R\right)$ is a bipartite graph

$\left(iii\right)$ $R$ has only two maximal ideals.

In view of Theorem 1.2, all rings are assumed to be non-local with identity, i.e., there are at least two maximal ideals in the ring.

2 Central sets in $\mathbb{G}\left(R\right)$

In 2016, Azadi et al. [8] studied the comaximal ideal graph and determined conditions for the distance between two vertices is 1 or 2 or 3. By using these results one can conclude the central sets. But unfortunately, after finalising our manuscript for publication we came across this journal. Though we share the same results provided by us is independent.

In this section, we determine independently certain central sets in the comaximal ideal graph and use the same to obtain the value of certain domination parameters of the comaximal ideal graph. By Theorem 1.4, if $\left|Max\left(R\right)\right|=2$, then the radius of $\mathbb{G}\left(R\right)$ is either one or two. Hence in this section, we assume that $R$ is a finite commutative ring with $\left|Max\left(R\right)\right|\ge 3$.

Remark 2.1

By Theorem 1.3, the radius of $\mathbb{G}\left(R\right)$ is one if and only if $R=F_1\times F_2$, where $F_1$ and $F_2$ are fields.

Let $R=R_1\times \cdots \times R_n\times F_1\times \cdots \times F_m$ be a finite commutative ring with $\left|Max\left(R\right)\right|\ge 3$, where each $(R_i,{\mathfrak{m}}_i)$ is a local ring but not a field and $F_j$ is a filed. Then $Max\left(R\right)=\{M_1,\dots ,M_n,M_1^{\prime },\dots ,M_m^{\prime }\}$, where $M_i=R_1\times \cdots \times R_{i-1}\times {\mathfrak{m}}_i\times R_{i+1}\times \cdots \times R_n\times F_1\times \cdots \times F_m$ and $M_k^{\prime }=R_1\times \cdots \times R_n\times F_1\times \cdots \times F_{k-1}\times \left(0\right)\times F_{k+1}\times \cdots \times F_m$ for $1\le i\le n$ and $1\le k\le m$.

Remark 2.2

Let $R=R_1\times \cdots \times R_n\times F_1\times \cdots \times F_m$ be a finite commutative ring with $\left|Max\left(R\right)\right|\ge 3$, where each $(R_i,{\mathfrak{m}}_i)$ is a local ring but not a field and $F_j$ is a filed. Then $\Delta \left(\mathbb{G}\left(R\right)\right)=de{g}_{\mathbb{G}\left(R\right)}\left(M\right)$ for some $M\in Max\left(R\right)$.

Theorem 2.3

Let $R=R_1\times \cdots \times R_n\times F_1\times \cdots \times F_m$ be a finite commutative ring with $\left|Max\left(R\right)\right|\ge 3$ , where each $(R_i,{\mathfrak{m}}_i)$ is a local ring but not a field and $F_j$ is a filed. Then the radius of $\mathbb{G}\left(R\right)$ is $2$ and the center of $\mathbb{G}\left(R\right)$ is $Max\left(R\right)$ .

Proof

Let $I={\prod }_{i=1}^n{I}_i\times {\prod }_{k=1}^m{I}_k^{\prime }$ be any ideal of $R$ with $I⊈\mathcal{J}\left(R\right)$, where $I_i$ is an ideal in $R_i$ and $I_k^{\prime }$ is an ideal in $F_k$.

Case 1. $m=0$. Then $I={\prod }_{i=1}^n{I}_i$.

By the assumption that $\left|Max\left(R\right)\right|\ge 3$, $n\ge 3$. For any ideal $K$ in $\mathbb{G}\left(R\right)$, $K$ is adjacent to some maximal ideal in $R$ and $M_i+M_j=R$ for $i\ne j$.

Suppose $I$ is maximal. Then $I=M_i$ for some $i$. Note that each $M_i$ is only not adjacent to $J=R_1\times \cdots \times R_{i-1}\times I_i\times R_{i+1}\times \cdots \times R_n$ for every ideal $I_i\subset {\mathfrak{m}}_i$. Then by definition, $J+M_k=R$ for all $k\ne i$ and so $I-M_k-J$ is a path of length $2$ in $\mathbb{G}\left(R\right)$. Hence $e\left(I\right)=2$ and so $e\left(I\right)=2$ for all $I\in Max\left(R\right)$.

Suppose $I$ is not maximal. Then $I\subset M_i$ for some $i$ and so $M_i+I\ne R$. If $I=R_1\times \cdots \times R_{i-1}\times I_i\times R_{i+1}\times \cdots \times R_n$ for $I_i\subset {\mathfrak{m}}_i$, then there exist an ideal $I^{\prime }=R_1\times \cdots \times R_{i-1}\times I_i\times R_{i+1}\times \cdots \times R_{j-1}\times I_j\times R_{j+1}\times R_n$ ($i\ne j$) for some $I_j\subset {\mathfrak{m}}_j$ such that $I^{\prime }+M_j\ne R$, $I+I^{\prime }\ne R$ and $I+M_j=R$. Since $I^{\prime }+M_k=R$ for some $k\ne i,k$, $I-M_j-M_k-I^{\prime }$ is a path of length $3$ and hence $e\left(I\right)=3$. From this, we have $e\left(I\right)=3$ for all ideal $I⊈\mathcal{J}\left(R\right)$ and $I\notin Max\left(R\right)$.

Case 2. $n=0$. Then $m\ge 3$ and $I={\prod }_{k=1}^m{I}_k^{\prime }$.

Suppose $I$ is maximal. Then $I=M_k^{\prime }$ for some $k$ and $I$ is not adjacent to $J$ for all $J={\prod }_{k=1}^m{J}_k^{\prime }$ with $J_k^{\prime }=\left(0\right)$, $J\ne M_k^{\prime }$ and $J⊈\mathcal{J}\left(R\right)$. Since $J+M_t^{\prime }=R$ for some $t$, $I-M_t^{\prime }-J$ is a path of length $2$, $e\left(I\right)=2$ and hence $e\left(I\right)=2$ for all $I\in Max\left(R\right)$.

If $I$ is not maximal, then $I_i^{\prime }=\left(0\right)$ and $I_t^{\prime }=\left(0\right)$ for some $i\ne t$ and so $I+M_i^{\prime }\ne R$, $I+M_t^{\prime }\ne R$. Since $m\ge 3$, there exist an ideal $I^{\prime }={\prod }_{\ell =1}^m{J}_{\ell }^{\prime }⊈\mathcal{J}\left(R\right)$ with $J_t^{\prime }=\left(0\right)$ such that $I+I^{\prime }\ne R$, $I^{\prime }+M_t\ne R$ and $I^{\prime }+M_i^{\prime }$. Since $I^{\prime }+M_j^{\prime }=R$ for $j\ne i,t$, $I-M_j-M_i^{\prime }-J$ is a path of length $3$ and so $e\left(I\right)=3$. From this, we have $e\left(I\right)=3$ for all ideal $I⊈\mathcal{J}\left(R\right)$ and $I\notin Max\left(R\right)$.

Case 3. $n\ge 1$ and $m\ge 1$. Then $n+m\ge 3$.

Let $I$ be any nonzero ideal of $R$ with $I⊈\mathcal{J}\left(R\right)$. Suppose $I$ is maximal. Note that any ideal is adjacent to some maximal ideal. If $J$ is an ideal not adjacent to $I$, then $J+M=R$ for some maximal ideal $M$ in $R$ and $M\ne I$ and so $I-M-J$ is a path of length $2$. Hence $e\left(I\right)=2$ for all $I\in Max\left(R\right)$.

Suppose $I$ is not maximal. Then $I\subset M$ for some $M\in Max\left(R\right)$. As in the proof of case 1 and case 2, we can find an ideals $I^{\prime }⊈\mathcal{J}\left(R\right)$ and $M^{\prime },M^{″}\in Max\left(R\right)$ such that $I^{\prime }$ is not maximal and $I-M^{\prime }-M^{″}-I^{\prime }$ is a path of length $3$ and hence $e\left(I\right)=3$. From this, we have $e\left(I\right)=3$ for all ideal $I⊈\mathcal{J}\left(R\right)$ and $I\notin Max\left(R\right)$.

Hence in all cases, the center of $\mathbb{G}\left(R\right)$ is $Max\left(R\right)$. □

Theorem 2.4

Let $R=R_1\times \cdots \times R_n\times F_1\times \cdots \times F_m$ be a finite commutative ring with $\left|Max\left(R\right)\right|\ge 3$ , where each $(R_i,{\mathfrak{m}}_i)$ is a local ring but not a field and $F_j$ is a filed. Then the median is a subset of the center of $\mathbb{G}\left(R\right)$ .

Proof

By Theorem 2.3, the radius of $\mathbb{G}\left(R\right)$ is $2$ and the center of $\mathbb{G}\left(R\right)$ is $Max\left(R\right)$. Let $k$ be the number of proper ideals in $\mathbb{G}\left(R\right)$. Let $I$ be any ideal in $R$ with $I⊈J\left(R\right)$. Suppose $I$ is maximal. Then (1) $$s\left(I\right)=de{g}_{\mathbb{G}\left(R\right)}\left(I\right)+2(k-1-de{g}_{\mathbb{G}\left(R\right)}\left(I\right))=2k-de{g}_{\mathbb{G}\left(R\right)}\left(I\right)-2$$(1) Note that Eq. (1) implies that all the vertices of the median must have the same degree. If $J$ is any ideal in $\mathbb{G}\left(R\right)$ but $J$ is not maximal, then there exists an ideal $J^{\prime }$ such that $d(J,J^{\prime })=3$ and so (2) $$s\left(J\right)>de{g}_{\mathbb{G}\left(R\right)}\left(J\right)+2(k-1-de{g}_{\mathbb{G}\left(R\right)}\left(J\right))=2k-de{g}_{\mathbb{G}\left(R\right)}\left(J\right)-2$$(2) Thus there is a maximal ideal $I$ with $s\left(I\right)<s\left(J\right)$ for $J\notin Max\left(R\right)$ and so any ideal not in the center of $\mathbb{G}\left(R\right)$ cannot be in the median of $\mathbb{G}\left(R\right)$. Hence the median is a subset of the center of $\mathbb{G}\left(R\right)$. □

Corollary 2.5

Let $R=R_1\times \cdots \times R_n\times F_1\times \cdots \times F_m$ be a finite commutative ring with $\left|Max\left(R\right)\right|\ge 3$ , where each $(R_i,{\mathfrak{m}}_i)$ is a local ring but not a field and $F_j$ is a filed. Then the median of $\mathbb{G}\left(R\right)$ is $\{M_j^{\prime }:1\le j\le m\}$ .

Proof

Let $k_i$ be the number of ideals in $R_i$ for $1\le i\le n$. Then $k_i\ge 3$. Clearly by the definition of $\mathbb{G}\left(R\right)$, $de{g}_{\mathbb{G}\left(R\right)}\left(M_i\right)=2^m{\prod }_{\stackrel{t=1}{t\ne i}}^n{k}_i-1$, $de{g}_{\mathbb{G}\left(R\right)}\left(M_j^{\prime }\right)=2^{m-1}{\prod }_{t=1}^n{k}_i-1$ and so $de{g}_{\mathbb{G}\left(R\right)}\left(M_i\right)<de{g}_{\mathbb{G}\left(R\right)}\left(M_j^{\prime }\right)$. By Eq. (1), $s\left(M_j^{\prime }\right)<s\left(M_i\right)$. Since $de{g}_{\mathbb{G}\left(R\right)}\left(M_j^{\prime }\right)=de{g}_{\mathbb{G}\left(R\right)}\left(M_{\ell }^{\prime }\right)$ for all $j\ne \ell$, $s\left(M_j^{\prime }\right)=s\left(M_{\ell }^{\prime }\right)$ for all $j\ne \ell$ and hence the median of $\mathbb{G}\left(R\right)$ is $\{M_j^{\prime }:1\le j\le m\}$. □

Corollary 2.6

Let $R=F_1\times \cdots \times F_m$ be a finite commutative ring with $\left|Max\left(R\right)\right|\ge 3$ , where each $F_i$ is a filed. Then the median and center of $\mathbb{G}\left(R\right)$ are equal.

Proof

This follows from Corollary 2.5. □

Theorem 2.7

Let $R=R_1\times \cdots \times R_n$ be a finite commutative ring with $\left|Max\left(R\right)\right|\ge 3$ , where each $(R_i,{\mathfrak{m}}_i)$ is a local ring but not a field. Let $k_i$ be the number of ideals in $R_i$ for $1\le i\le n$ . Then the median and center of $\mathbb{G}\left(R\right)$ are equal if and only if $k_i=k_j$ for all $i\ne j$ .

Proof

Suppose $k_i=k_j$ for all $i\ne j$. Then by definition of $\mathbb{G}\left(R\right)$, $de{g}_{\mathbb{G}\left(R\right)}\left(M_i\right)=de{g}_{\mathbb{G}\left(R\right)}\left(M_j\right)$ for all $i\ne j$. By Theorems 2.3 and 2.4, the median of $\mathbb{G}\left(R\right)$ is $Max\left(R\right)$.

Conversely, assume that the median and center of $\mathbb{G}\left(R\right)$ are equal. As in proof of Theorem 2.3, the median of $\mathbb{G}\left(R\right)$ is $Max\left(R\right)$. Suppose $k_i\ne k_j$ for some $i\ne j$. Without loss of generality, we assume that $k_i<k_j$. Then $de{g}_{\mathbb{G}\left(R\right)}\left(M_j\right)<de{g}_{\mathbb{G}\left(R\right)}\left(M_i\right)$ and so $s\left(M_i\right)<s\left(M_j\right)$, a contradiction. □

The following result proved by Meng Ye et al. [7, Theorem 4.8] is used frequently and hence given below.

Theorem 2.8

[7, Theorem 4.8] $\left(1\right)$ For a ring $R$ , $\mathbb{G}\left(R\right)$ is the finite complete bipartite graph $K_{n,m}$ (where $n$ and $m$ are finite integers) if and only if $R\cong R_1\times R_2$ , where $R_1$ and $R_2$ are artinian local rings with $n+1$ and $m+1$ ideals respectively.

$\left(2\right)$ For a ring $R$ , $\mathbb{G}\left(R\right)$ is a finite star graph $K_{1,n}$ if and only if $R\cong F\times R_1$ , where $F$ is a field and $R_1$ is an artinian local ring with exactly $n+1$ ideals.

In view of Theorem 2.8(2), we have the following, $\gamma \left(\mathbb{G}\left(R\right)\right)=1$ if and only if $R\cong F\times R_1$, where $F$ is a field and $R_1$ is an artinian local ring.

Also $\gamma \left(\mathbb{G}\left(R\right)\right)=2$ if and only if $R\cong R_1\times R_2$, where each $R_i$ is an artinian local ring but not a field.

Theorem 2.9

Let $R=R_1\times \cdots \times R_n\times F_1\times \cdots \times F_m$ be a finite commutative ring with $\left|Max\left(R\right)\right|\ge 3$ , where each $(R_i,{\mathfrak{m}}_i)$ is a local ring but not a field and $F_j$ is a filed. Then $\gamma \left(\mathbb{G}\left(R\right)\right)=\left|Max\left(R\right)\right|$ .

Proof

Let $D=\{M_1,\dots ,M_n,M_1^{\prime },\dots ,M_m^{\prime }\}=Max\left(R\right)$. Let $I$ be any ideal in $\mathbb{G}\left(R\right)$. Then by definition, $I$ is adjacent to some maximal ideal in $R$. Hence $D$ is a dominating set of $\mathbb{G}\left(R\right)$ and so $\gamma \left(\mathbb{G}\left(R\right)\right)\le n+m$.

Suppose $S$ is a dominating set for $\mathbb{G}\left(R\right)$. Since $\mathbb{G}\left(R\right)$ has no vertex adjacent to all others, $\left|S\right|\ge 2$. For each $k=1,2,\dots ,n+m$, let $A_k={\prod }_{i=1}^{n+m}{I}_i$, where $I_k\ne \left(0\right)$ or $F_k$ and $I_j=R_j$ or $F_j$ for all $j\ne k$. For each $k=1,2,\dots ,n+m$, let $B_k={\prod }_{i=1}^{n+m}{I}_i$, where $I_k=R_k$ or $F_k$ and $I_j\ne R_j$ or $F_j$ for all $j\ne k$. Then, each $A_k$ and $B_k$ is a vertex of $\mathbb{G}\left(R\right)$. For each $k=1,2,\dots ,n+m$, the element $B_k$ is only adjacent with the element $A_k$. That is, for each $k$, either $A_k\in S$ or $B_k\in S$. Thus $S$ contains at least $n+m$ elements and so $\gamma \left(\mathbb{G}\left(R\right)\right)=n+m$. □

In view of Theorem 2.9, we have the following, $Max\left(R\right)$ is a $\gamma$-set of $\mathbb{G}\left(R\right)$.

Theorem 2.10

Let $R=R_1\times \cdots \times R_n\times F_1\times \cdots \times F_m$ be a finite commutative ring with $\left|Max\left(R\right)\right|\ge 3$ , where each $(R_i,{\mathfrak{m}}_i)$ is a local ring but not a field and $F_j$ is a filed. Then $i\left(\mathbb{G}\left(R\right)\right)\le \left|V\left(\mathbb{G}\left(R\right)\right)\right|-\Delta \left(\mathbb{G}\left(R\right)\right)$ .

Proof

For each $M\in Max\left(R\right)$, $V\left(\mathbb{G}\left(R\right)\right)-N_{\mathbb{G}\left(R\right)}\left(M\right)$ is an independent set of $\mathbb{G}\left(R\right)$. Let $M\in Max\left(R\right)$ with $\Delta \left(\mathbb{G}\left(R\right)\right)=de{g}_{\mathbb{G}\left(R\right)}\left(M\right)$. Then $V\left(\mathbb{G}\left(R\right)\right)-N_{\mathbb{G}\left(R\right)}\left(M\right)$ is an independent dominating set of $\mathbb{G}\left(R\right)$ and so $i\left(\mathbb{G}\left(R\right)\right)\le \left|V\left(\mathbb{G}\left(R\right)\right)\right|-\Delta \left(\mathbb{G}\left(R\right)\right)$. □

3 Isomorphism properties of $\mathbb{G}\left(R\right)$ and planarity of $\mathbb{G}\left(R\right)$

Consider the question: If $R$ and $S$ are two rings with $\mathbb{G}\left(R\right)\cong \mathbb{G}\left(S\right)$, then do we have $R\cong S?$ The following example shows that the above question is not valid in general.

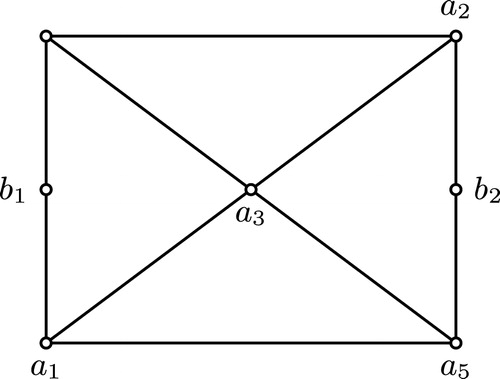
Example 3.1

Let $R={\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{Z}}_5$ and $S={\mathbb{Z}}_7\times {\mathbb{Z}}_{11}\times {\mathbb{Z}}_{13}$. Then $\mathbb{G}\left(R\right)\cong \mathbb{G}\left(S\right)$ (see. Fig. 3.1). But $R$ and $S$ are not isomorphic.

Fig. 3.1. $\mathbb{G}\left(R\right)\cong \mathbb{G}\left(S\right)$

Theorem 3.2

Let $R={\prod }_{i=1}^n{R}_i\times {\prod }_{j=1}^m{F}_j$ and $S={\prod }_{i=1}^n{R}_i^{\prime }\times {\prod }_{j=1}^m{F}_j^{\prime }$ be finite commutative rings with $n+m\ge 2$ , where each $(R_i,{\mathfrak{m}}_i)$ and $(R_i,{\mathfrak{m}}_i^{\prime })$ are local rings but not field and each $F_i$ and $F_j^{\prime }$ are field. Let $k_i$ be the number of ideals in $R_i$ and $k_i^{\prime }$ be the number of ideals in $R_i^{\prime }$ . Then $\mathbb{G}\left(R\right)\cong \mathbb{G}\left(S\right)$ if and only if $k_i=k_i^{\prime }$ for all $i$ , $1\le i\le n$ .

Proof

If $R\cong S$, then the result is obvious. Assume that $R\ncong S$. Suppose $k_i=k_i^{\prime }$ for all $i$, $1\le i\le n$. Then $\left|V\left(\mathbb{G}\left(R\right)\right)\right|=\left|V\left(\mathbb{G}\left(S\right)\right)\right|$. Let $I_j\left(R_j\right)=\{I_{1j}=\left(0\right),I_{2j}={\mathfrak{m}}_j,I_{3j},\dots ,I_{k_{j}j}=R_j\}$ be the set of ideals in $R_j$ and $I_j^{\prime }\left(R_j^{\prime }\right)=\{I_{1j}^{\prime }=\left(0\right),I_{2j}^{\prime }={\mathfrak{m}}_j,I_{3j}^{\prime },\dots ,I_{k_{j}j}^{\prime }=R_j^{\prime }\}$ be the set of ideals in $R_j^{\prime }$. Then the map $I_{tj}\to I_{tj}^{\prime }$ is a bijection from $I_j\left(R_j\right)$ onto $I_j^{\prime }\left(R_j^{\prime }\right)$. Define $\varphi :V\left(\mathbb{G}\left(R\right)\right)⟶V\left(\mathbb{G}\left(S\right)\right)$ by $\varphi ({\prod }_{i=1}^n{I}_{ti}\times {\prod }_{j=1}^m{J}_j)={\prod }_{i=1}^n{I}_{ti}^{\prime }\times {\prod }_{j=1}^m{J}_j^{\prime }$ where $$J_j^{\prime }=\left\{\begin{array}{cc}{F}_j^{\prime }\hfill & \text{if}{J}_j=F_j\hfill \\ \left(0\right)\hfill & \text{if}{J}_j=\left(0\right)\hfill \end{array}\right.$$Then $\varphi$ is well-defined and bijective. Let $I={\prod }_{i=1}^n{I}_i\times {\prod }_{j=1}^m{J}_j$ and $J={\prod }_{i=1}^n{A}_i\times {\prod }_{j=1}^m{B}_j$ be two non-zero ideals in $R$. Suppose $I$ and $J$ are adjacent in $\mathbb{G}\left(R\right)$. Then $I+J=R$ and so $I_i+A_i=R_i$ and $J_j+B_j=F_j$ for all $i,j$. Let $f\left(I\right)={\prod }_{i=1}^n{I}_i^{\prime }\times {\prod }_{j=1}^m{J}_j^{\prime }$ and $f\left(J\right)={\prod }_{i=1}^n{A}_i^{\prime }\times {\prod }_{j=1}^m{B}_j^{\prime }$. By definition of $\varphi$, $I_i^{\prime }+A_i^{\prime }=R_i^{\prime }$ and $J_j^{\prime }+B_j^{\prime }=F_j$ for all $i,j$ and so $f\left(I\right)+f\left(J\right)=S$. Hence $f\left(I\right)$ and $f\left(J\right)$ are adjacent in $\mathbb{G}\left(S\right)$. Similarly one can prove that $f$ preserves non-adjacency also. Hence $\mathbb{G}\left(R\right)\cong \mathbb{G}\left(S\right)$.

Conversely, assume that $\mathbb{G}\left(R\right)\cong \mathbb{G}\left(S\right)$. Suppose $k_i\ne k_i^{\prime }$ for some $i$. Then $\left|V\left(\mathbb{G}\left(R\right)\right)\right|\ne \left|V\left(\mathbb{G}\left(S\right)\right)\right|$, a contradiction. Hence $k_i=k_i^{\prime }$ for all $i$. □

Example 3.3

Let $R={\mathbb{Z}}_4\times {\mathbb{Z}}_2$ and $S={\mathbb{Z}}_9\times {\mathbb{Z}}_3$. Then $\mathbb{G}\left(R\right)\cong \mathbb{G}\left(S\right)\cong K_{1,2}$ (by Theorem 2.8). But $R$ and $S$ are not isomorphic.

Using Theorem 3.2, one can have the following corollary.

Corollary 3.4

Let $R_1={\prod }_{i=1}^n{F}_i$ and $R_2={\prod }_{j=1}^n{F}_i^{\prime }$ , where each $F_i$ and $F_j^{\prime }$ are fields and $n\ge 2$ . Then $\mathbb{G}\left(R_1\right)\cong \mathbb{G}\left(R_2\right)$ .

Corollary 3.5

Let $R={\prod }_{i=1}^n{R}_i$ and $S={\prod }_{i=1}^n{R}_i^{\prime }$ be finite commutative rings with $n\ge 2$ , where each $(R_i,{\mathfrak{m}}_i)$ and $(R_i,{\mathfrak{m}}_i^{\prime })$ are local rings but not field. Let $k_i$ be the number of ideals in $R_i$ and $k_i^{\prime }$ be the number of ideals in $R_i^{\prime }$ . Then $\mathbb{G}\left(R\right)\cong \mathbb{G}\left(S\right)$ if and only if $k_i=k_i^{\prime }$ for all $i$ , $1\le i\le n$ .

In view of the above it is natural to consider the question that whether the comaximal-ideal graph is isomorphic to the zero-divisor graph or the annihilating ideal graph. In [7], it has been proved that for a finite commutative ring $R={\prod }_{i=1}^n{F}_i$, where $F_i$ is field and $n\ge 2$, the co-maximal graph $\mathbb{G}\left(R\right)$ of $R$ is isomorphic to the zero-divisor graph of ${\mathbb{Z}}_2^n$. In this section, we prove that the comaximal ideal graph of a particular ring is isomorphic to the annihilating-ideal graph of an another ring.

Theorem 3.6

Let $R_1={\mathbb{Z}}_2^n$ and $R_2={\prod }_{k=1}^n{F}_k$ where each $F_i$ is a field and $n\ge 2$ . Let $\Gamma \left(R_1\right)$ be the zero-divisor graph of $R_1$ . Then $\mathbb{G}\left(R_2\right)\cong \mathbb{AG}\left(R_2\right)\cong \Gamma \left(R_1\right)$ .

Proof

Note that $V\left(\mathbb{AG}\left(R_2\right)\right)=\{I={\prod }_{i=1}^n{I}_i:I_i\in \{\left(0\right),F_i\},1\le i\le n\}\setminus ︀\{\left(0\right),R_2\}$, $V\left(\Gamma \left(R_1\right)\right)=\{a=(a_1,a_2,\dots ,a_n):a_i\in \{0,1\},1\le i\le n\}\setminus ︀\{(0,0,\dots ,0),(1,1\dots ,1)\}$ and $\left|V\left(\mathbb{AG}\left(R_2\right)\right)\right|=\left|V\left(\Gamma \left(R_1\right)\right)\right|=2^n-2$.

Define $f:V\left(\mathbb{AG}\left(R_2\right)\right)⟶V\left(\Gamma \left(R_1\right)\right)$ by $f\left({\prod }_{i=1}^n{I}_i\right)=(a_1,a_2,\dots ,a_n)$ where $$a_i=\left\{\begin{array}{cc}1\hfill & \text{if}{I}_i=F_i\hfill \\ 0\hfill & \text{if}{I}_i=\left(0\right)\hfill \end{array}\right.$$Clearly $f$ is well-defined and bijective. Let $I={\prod }_{i=1}^n{I}_i$ and $I^{\prime }={\prod }_{i=1}^n{I}_i^{\prime }$ be two non-zero ideals in $R_2$. Suppose $I$ and $I^{\prime }$ are adjacent in $\mathbb{AG}\left(R_2\right)$. Then $I{I}^{\prime }=\left(0\right)$ and so $I_i{I}_i^{\prime }=\left(0\right)$ for all $i$. Hence $I_i=\left(0\right)$ or $I_i^{\prime }=\left(0\right)$ for all $i$. Suppose $f\left(I\right)=(b_1,b_2,\dots ,b_n)$ and $f\left(I^{\prime }\right)=(c_1,c_2,\dots ,c_n)$. Then either $b_i=0$ or $c_i=0$ and so $b_i{c}_i=0$ for all $i$. i.e, $f\left(I\right)f\left(I^{\prime }\right)=0$ and so $f\left(I\right)$ and $f\left(I^{\prime }\right)$ are adjacent in $\Gamma \left(R_1\right)$. Similarly one can prove that $f$ preserves non-adjacency also. Hence $\mathbb{AG}\left(R_2\right)\cong \Gamma \left(R_1\right)\cong \mathbb{G}\left(R_2\right)$. □

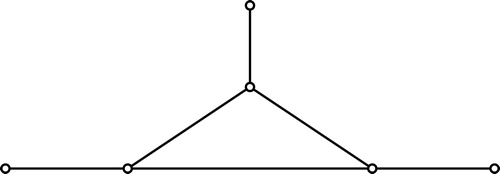
In [8], Azadi et al. have proved that the comaximal ideal graph is planar, when $\left|max\left(R\right)\right|=4$. But here we proved that the comaximal ideal graph is non-planar, when $\left|max\left(R\right)\right|\ge 4$ by the simple observation of the following remark. In [9], Visweswaran et al. have characterized the commutative ring whose comaxial ideal graph is planar. Here we give a simple proof of the same.

Remark 3.7

Note that if $n\ge 4$, then $\Gamma \left({\mathbb{Z}}_2^n\right)$ is nonplanar. Hence if $R={\prod }_{i=1}^n{F}_i$ where $F_i$ is field and $n\ge 2$. Then $\mathbb{G}\left(R\right)$ is planar if and only if $R\cong F_1\times F_2$ or $R\cong F_1\times F_2\times F_3$.

Theorem 3.8

Let $R={\prod }_{i=1}^n{R}_i\times {\prod }_{j=1}^m{F}_j$ be a finite commutative ring with $n+m\ge 2$ , where each $(R_i,{\mathfrak{m}}_i)$ is a local ring but not field and each $F_i$ is a field. Then $\mathbb{G}\left(R\right)$ is planar if and only if $R$ satisfies any one of the following conditions: $\left(i\right)$ $F_1\times F_2\times F_3$ or $R_1\times F_1\times F_2$ and ${\mathfrak{m}}_1$ is the only nonzero proper ideal in $R_1$ $\left(ii\right)$ $F_1\times F_2$ or $R_1\times F_1$ $\left(iii\right)$ $R_1\times R_2$ where $R_1$ has at most $3$ nonzero ideals and $R_2$ has at most $2$ nonzero ideals and $R_1$ has at most $2$ nonzero ideals and $R_2$ has at most $3$ nonzero ideals.

Proof

Suppose $\mathbb{G}\left(R\right)$ is planar. Note that $\Gamma \left({\mathbb{Z}}_2^{n+m}\right)$ is a subgraph of $\mathbb{G}\left(R\right)$. Suppose $n+m\ge 4$. Since $\Gamma \left({\mathbb{Z}}_2^{n+m}\right)$ is nonplanar, $\mathbb{G}\left(R\right)$ is nonplanar and hence $n+m\le 3$.

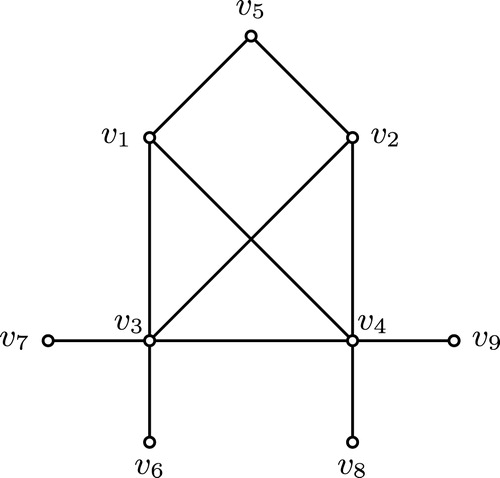
Case 1.Suppose $n+m=3$.

subcase 1. $n=0$ and $m=3$. Then by Remark 3.7, $R=F_1\times F_2\times F_3$.

subcase 2. $m=0$ and $n=3$. Let $\Omega =\{x_1,x_2,x_3,y_1,y_2,y_3,z_1,z_2,z_3\}$ where $x_1={\mathfrak{m}}_1\times R_2\times R_3$, $x_2=R_1\times {\mathfrak{m}}_2\times R_3$, $x_3=R_1\times R_2\times {\mathfrak{m}}_3$, $y_1=\left(0\right)\times R_2\times R_3$, $y_2=R_1\times \left(0\right)\times R_3$, $y_3=R_1\times R_2\times \left(0\right)$, $z_1=R_1\times \left(0\right)\times \left(0\right)$, $z_2=\left(0\right)\times R_2\times \left(0\right)$, $z_3=\left(0\right)\times \left(0\right)\times R_3$. Then $〈\Omega 〉$ is a subgraph of $\mathbb{G}\left(R\right)$, $〈\Omega 〉$ contains a subdivision of $K_{3,3}$ (see Fig. 3.2(a)) and hence $\mathbb{G}\left(R\right)$ is nonplanar.

Fig. 3.2(a). ($〈\Omega 〉$) is a subgraph of $\mathbb{G}\left(R\right)$

subcase 3. If $n=2$ and $n=1$, then $R=R_1\times R_2\times F_1$.

Let ${\Omega }^{\prime }=\{a_1,a_2,a_3,a_4,a_5,b_1,b_2\}$ where $a_1={\mathfrak{m}}_1\times R_2\times F_1$, $a_2=R_1\times {\mathfrak{m}}_2\times F_1$, $a_3=R_1\times R_2\times \left(0\right)$, $a_4=\left(0\right)\times R_2\times F_1$, $a_5=R_1\times \left(0\right)\times F_1$, $b_1=R_1\times \left(0\right)\times \left(0\right)$, $b_2=\left(0\right)\times R_2\times \left(0\right)$. Then $〈{\Omega }^{\prime }〉$ is a subgraph of $\mathbb{G}\left(R\right)$, $〈{\Omega }^{\prime }〉$ contains a subdivision of $K_5$ (see Fig. 3.2(b)) and hence $\mathbb{G}\left(R\right)$ is nonplanar.

Fig. 3.2(b). ($〈{\Omega }^{\prime }〉$) is a subgraph of $\mathbb{G}\left(R\right)$

subcase 4. If $m=1$ and $n=2$, then $R=R_1\times F_1\times F_2$. Suppose $I$ is any nonzero proper ideal in $R_1$ and $I\subset {\mathfrak{m}}_1$. Let ${\Omega }^{″}=\{d_1,d_2,d_3,e_1,e_2,e_3\}$ where $d_1={\mathfrak{m}}_1\times F_1\times F_2$, $d_2=I\times F_1\times F_2$, $d_3=\left(0\right)\times F_1\times F_2$, $e_1=R_1\times \left(0\right)\times \left(0\right)$, $e_2=R_1\times \left(0\right)\times F_2$, $e_2=R_1\times F_1\times \left(0\right)$. Then $〈{\Omega }^{″}〉$ is a subgraph of $\mathbb{G}\left(R\right)$, $〈{\Omega }^{″}〉$ contains a $K_{3,3}$ as a subgraph and so $\mathbb{G}\left(R\right)$ is nonplanar. Hence ${\mathfrak{m}}_1$ is only nonzero proper ideal in $R_1$. Let $V\left(\mathbb{G}\left(R\right)\right)=\{v_1,\dots ,v_9\}$ where $v_1=\left(0\right)\times F_1\times F_2$, $v_2={\mathfrak{m}}_1\times F_1\times F_2,v_3=R_1\times \left(0\right)\times F_2,v_4=R_1\times F_1\times \left(0\right),v_5=R_1\times \left(0\right)\times \left(0\right)$, $v_6=\left(0\right)\times F_1\times \left(0\right),v_7={\mathfrak{m}}_1\times F_1\times \left(0\right)$, $v_8=\left(0\right)\times \left(0\right)\times F_2$, $v_9={\mathfrak{m}}_1\times \left(0\right)\times F_2$. Since $\mathbb{G}\left(R\right)$ is planar and by Fig. 3.2(c), $R\cong R_1\times F_1\times F_2$ and ${\mathfrak{m}}_1$ is only nonzero proper ideal in $R_1$.

Fig. 3.2(c). $\mathbb{G}\left(R\right)$

Case 2. $n+m=2$. Then by Theorem 2.8, $\mathbb{G}\left(R\right)$ is a complete bipartite graph. Since $\mathbb{G}\left(R\right)$ is planar, $R\cong R_1\times F_1$ or $F_1\times F_2$.

If $R\cong R_1\times R_2$, then by Theorem 2.8, $\mathbb{G}\left(R\right)\cong K_{t,k}$ where $t$ and $k$ are number of nonzero ideals in $R_1$ and $R_2$ respectively. Since $\mathbb{G}\left(R\right)$ is planar, either $t\le 3$ and $k\le 2$ or $t\le 2$ or $k\le 3$.

Converse is obvious. □

Acknowledgments

The authors wish to record their sincere thanks to the anonymous referees for carefully reading the manuscript and making suggestions that improve the content and presentation of the paper.