A new matrix representation of multidigraphs

Abstract

In this article, we introduce a new matrix associated with a multidigraph, named as the complex adjacency matrix. We study the spectral properties of bipartite multidigraphs corresponding to the complex adjacency matrix. It is well known that a simple undirected graph is bipartite if and only if the spectrum of its adjacency matrix is symmetric about the origin (with multiplicity). We show that the result is not true in general for multidigraphs and supply a class of non-bipartite multidigraphs which have this property. We describe the complete spectrum of a multi-directed tree in terms of the spectrum of the corresponding modular tree. As a consequence, we get a class of Hermitian matrices for which the spectrum of a matrix in the class and the spectrum of the modulus (entrywise) of the matrix are the same.

Keywords:

• Multidigraph
• Complex adjacency matrix
• Complex adjacency spectrum
• SO-property

1 Introduction

Throughout this article, we consider multidigraphs without having self-loops. By a multidigraph, we mean a digraph (directed graph), where multiple directed edges between pair of vertices are allowed (see [1]). Two vertices in a multidigraph are said to be adjacent if there is at least one directed edge between them. Treating each undirected edge as equivalent to two oppositely oriented directed edges with the same end vertices, the class of all undirected graphs may be viewed as a subclass of the class of multidigraphs.

The adjacency matrix is a popular matrix representation of a graph and the relationship between the eigenvalues of adjacency matrix with the graph structure has been studied by many researchers in the past, see for example [1,2]. For a multidigraph $G$ on $n$ vertices, the adjacency matrix of $G$ is defined [1] as the $n\times n$ matrix $A\left(G\right)=\left[a_{ij}\right]$, whose $ij$th entry $a_{ij}$ is equal to the number of directed edges originating from the vertex $i$ and terminating at the vertex $j$. From the definition, it is clear that the adjacency matrix of a multidigraph is not symmetric, in general. So it may have complex eigenvalues. As a result, the comparison of eigenvalues for different multidigraphs is not possible because the interlacing results [3] cannot be applied. Furthermore, it is known that not only the eigenvalues but also the eigenvectors of different matrix representations of an undirected graph carry information about the structure of a graph, see for example [4–6] and the references therein. Moreover, a graph is completely determined by its adjacency eigenvalues and the corresponding eigenvectors. This is evident from the fact that a graph $G$ is uniquely determined by $A\left(G\right)$. If $G$ is an undirected simple graph, then $A\left(G\right)$ is symmetric. Thus, if $x_1,x_2,\dots ,x_n$ are $n$ linearly independent eigenvectors of $A\left(G\right)$ corresponding to the eigenvalues ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$, respectively, consider the $n\times n$ matrix $\mathcal{V}$ with columns as $x_i$, then $A\left(G\right)=\mathcal{V}\Lambda {\mathcal{V}}^T$, where $\Lambda =\text{diag}({\lambda }_1,\dots ,{\lambda }_n)$. 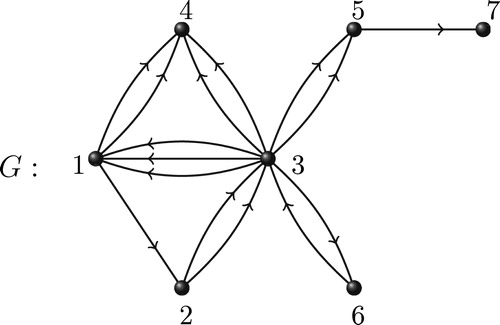But, the adjacency matrix of a multidigraph most often fails to possess a complete set of linearly independent eigenvectors. There may be some eigenvalues of the matrix for which geometric multiplicity is less than its algebraic multiplicity. For example, consider the following multidigraph.

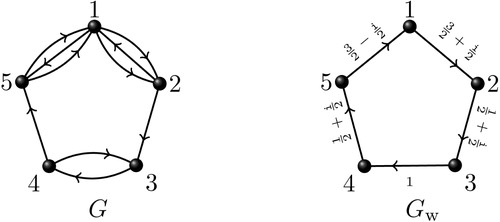
Example 1

Consider the multidigraph $G$ in Fig. 1. The known adjacency matrix of $G$ is given by $$A\left(G\right)=\left[\begin{array}{ccccccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill 2\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$$Notice that it is an asymmetric real matrix of order $7$ and its characteristic polynomial is given by $$\varphi (A\left(G\right),x)=x^7-x^5-6x^4=x^4(x-2)(x+1-\sqrt{2}i)(x+1+\sqrt{2}i).$$So the eigenvalues of $A\left(G\right)$ are $2,-1-\sqrt{2}i,-1+\sqrt{2}i$ and $0$ (algebraic multiplicity of $0$ is $4$ and that of other eigenvalues is $1$ each). The corresponding eigenvectors are given by $$\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 2\hfill \\ \hfill 2\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{c}\hfill \frac{-1+\sqrt{2}i}{3}\hfill \\ \hfill 1\hfill \\ \hfill \frac{-1-\sqrt{2}i}{2}\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill \frac{1}{2}\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{c}\hfill \frac{-1}{1-\sqrt{2}i}\hfill \\ \hfill 1\hfill \\ \hfill \frac{-1+\sqrt{2}i}{2}\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill \frac{1}{2}\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill -3\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{c}\hfill 0\hfill \\ \hfill -2\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \\ \hfill -2\hfill \\ \hfill 0\hfill \end{array}\right)\text{and}\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \\ \hfill -2\hfill \\ \hfill 0\hfill \end{array}\right),$$respectively. The last three linearly independent eigenvectors correspond to the $0$ eigenvalue. Note here that the geometric multiplicity of $0$ is one less than its algebraic multiplicity.

Fig. 1 A multidigraph $G$ on $7$ vertices.

To avoid the above described difficulty, we associate a new Hermitian matrix to a multidigraph, which reduces to the usual adjacency matrix in case of an undirected simple graph, when each undirected edge is treated as a pair of oppositely oriented edges. Let $i$ denote $\sqrt{-1}$, the imaginary unit.

Definition 2

Let $G=(V,E)$ be a multidigraph with $V=\{1,2,\dots ,n\}$. Let $b_{ij}$ and $f_{ij}$ denote the number of directed edges from $j$ to $i$ and from $i$ to $j$, respectively. Then the complex adjacency matrix $A_{ℂ}\left(G\right)$ of $G$ is an $n\times n$ matrix $A_{ℂ}\left(G\right)=\left[a_{ij}\right]$ whose rows and columns are indexed by $V$ and the $ij$th entry is given by $$a_{ij}=\frac{(f_{ij}+b_{ij})}{2}+\frac{(f_{ij}-b_{ij})}{2}\times i.$$

The eigenvalues and eigenvectors of $A_{ℂ}\left(G\right)$ are called the $A_{ℂ}$-eigenvalues and $A_{ℂ}$-eigenvectors of $G$, respectively. The spectrum of $A_{ℂ}\left(G\right)$ is called the complex adjacency spectrum (or in short $A_{ℂ}$-spectrum ) of $G$ and is denoted by ${\sigma }_{A_{ℂ}}\left(G\right)$. Note that $A_{ℂ}\left(G\right)$ is Hermitian, so all its eigenvalues are real and we have a complete set of linearly independent eigenvectors.

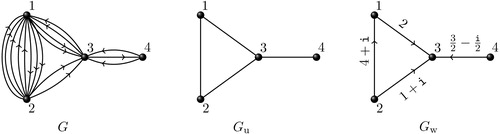
Example 3

Consider the multidigraph $G$ in Fig. 1. The complex adjacency matrix of $G$ is given by $$A_{ℂ}\left(G\right)=\left[\begin{array}{ccccccc}\hfill 0\hfill & \hfill \frac{1}{2}+\frac{i}{2}\hfill & \hfill \frac{3}{2}-\frac{3i}{2}\hfill & \hfill 1+i\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{1}{2}-\frac{i}{2}\hfill & \hfill 0\hfill & \hfill 1+i\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{3}{2}+\frac{3i}{2}\hfill & \hfill 1-i\hfill & \hfill 0\hfill & \hfill 1+i\hfill & \hfill 1+i\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1-i\hfill & \hfill 0\hfill & \hfill 1-i\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1-i\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{2}+\frac{i}{2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{2}-\frac{i}{2}\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].$$It is a complex Hermitian matrix of order $7$ and its characteristic polynomial is given by $$\varphi (A_{ℂ}\left(G\right),x)=x^7-\frac{29}{2}{x}^5-3x^4+\frac{37}{2}{x}^3+\frac{3}{2}{x}^2-\frac{15}{4}x.$$The eigenvalues of $A_{ℂ}\left(G\right)$ (correct to $4$ places of decimals) are $-3.4903,-1.1707,-0.5319$, $0,0.4670,0.9885$ and 3.7375, and the corresponding eigenvectors are $$\left(\begin{array}{c}\hfill -0.4316-0.2239i\hfill \\ \hfill 0.2859-0.2217i\hfill \\ \hfill 0.0000+0.6701i\hfill \\ \hfill -0.0042-0.2515i\hfill \\ \hfill -0.2002-0.2002i\hfill \\ \hfill 0.0000-0.1920i\hfill \\ \hfill 0.0574\hfill \end{array}\right),\left(\begin{array}{c}\hfill -0.5163+0.0457i\hfill \\ \hfill 0.0203-0.0593i\hfill \\ \hfill 0.0000-0.2116i\hfill \\ \hfill 0.5827-0.2993i\hfill \\ \hfill 0.2845+0.2845i\hfill \\ \hfill -0.0000+0.1807i\hfill \\ \hfill -0.2430\hfill \end{array}\right),\left(\begin{array}{c}\hfill -0.1172+0.0784i\hfill \\ \hfill -0.2352+0.0879i\hfill \\ \hfill 0.0000-0.1445i\hfill \\ \hfill 0.3447-0.0960i\hfill \\ \hfill -0.3542-0.3542i\hfill \\ \hfill -0.0000+0.2717i\hfill \\ \hfill 0.6659\hfill \end{array}\right),\left(\begin{array}{c}\hfill -0.0000+0.0000i\hfill \\ \hfill -0.3082+0.4144i\hfill \\ \hfill 0.0000+0.0000i\hfill \\ \hfill 0.1541-0.2072i\hfill \\ \hfill 0.0000+0.0000i\hfill \\ \hfill -0.4674-0.6694i\hfill \\ \hfill 0\hfill \end{array}\right),$$ $$\left(\begin{array}{c}\hfill 0.0217-0.1952i\hfill \\ \hfill -0.5390+0.1210i\hfill \\ \hfill 0.0000+0.1649i\hfill \\ \hfill -0.0184-0.1111i\hfill \\ \hfill -0.2732-0.2732i\hfill \\ \hfill 0.0000+0.3532i\hfill \\ \hfill -0.5850\hfill \end{array}\right),\left(\begin{array}{c}\hfill -0.0585-0.4222i\hfill \\ \hfill -0.4299+0.0028i\hfill \\ \hfill 0.0000+0.1846i\hfill \\ \hfill -0.2995-0.1811i\hfill \\ \hfill 0.3824+0.3824i\hfill \\ \hfill 0.0000+0.1867i\hfill \\ \hfill 0.3868\hfill \end{array}\right)\text{and}\left(\begin{array}{c}\hfill -0.2615-0.4318i\hfill \\ \hfill 0.0815-0.1970i\hfill \\ \hfill 0.0000-0.6511i\hfill \\ \hfill -0.3597-0.2198i\hfill \\ \hfill -0.1807-0.1807i\hfill \\ \hfill 0.0000-0.1742i\hfill \\ \hfill -0.0483\hfill \end{array}\right),\text{respectively.}$$

Thus, all the eigenvalues of $A_{ℂ}\left(G\right)$ are real and we have exactly $7$ mutually orthogonal eigenvectors.

Notice that, twice the real part of the $ij$th entry of $A_{ℂ}\left(G\right)$ is equal to the total number of directed edges between $i$ and $j$ and the imaginary part stands for the effective/resultant orientation of directed edges from $i$ to $j$. So, if we view an undirected graph as a multidigraph by considering an edge of the graph same as two oppositely oriented directed edges, then the complex adjacency matrix of a graph is same as its adjacency matrix. Given a multidigraph $G$, the adjacency matrix $A\left(G\right)$ and the complex adjacency matrix $A_{ℂ}\left(G\right)$ of a multidigraph $G$ are related in the following way: $$A\left(G\right)=\text{Re}\left(A_{ℂ}\left(G\right)\right)+\text{Im}\left(A_{ℂ}\left(G\right)\right).$$In a more descriptive way, if $A_{ℂ}\left(G\right)=\left[c_{ij}\right]$ and $A\left(G\right)=\left[a_{ij}\right]$, then $$c_{ij}=\left(\frac{a_{ij}+a_{ji}}{2}\right)+\left(\frac{a_{ij}-a_{ji}}{2}\right)i.$$

Now that we have a Hermitian matrix associated to a multidigraph, we can always compare complex adjacency spectra of two multidigraphs on a given number of vertices. Using the interlacing results for Hermitian matrices [3], we have the following immediate results.

Lemma 4

Let $G$ be a multidigraph on vertices $1,\dots ,n$ and $H$ be a multidigraph produced from $G$ by deleting a directed edge $e$ from $G$ . If ${\lambda }_1\left(G\right)\le {\lambda }_2\left(G\right)\le \cdots \le {\lambda }_n\left(G\right)$ and ${\lambda }_1\left(H\right)\le {\lambda }_2\left(H\right)\le \cdots \le {\lambda }_n\left(H\right)$ are the $A_{ℂ}$ -eigenvalues of $G$ and $H$ , respectively, then ${\lambda }_1\left(G\right)\le {\lambda }_2\left(H\right);{\lambda }_{i-1}\left(H\right)\le {\lambda }_i\left(G\right)\le {\lambda }_{i+1}\left(H\right)$ , for $i=2,\dots ,n-1$ , and ${\lambda }_{n-1}\left(H\right)\le {\lambda }_n\left(G\right)$ .

Proof

Suppose that the deleted directed edge of $G$ is $e=(i,j)$. Then $A_{ℂ}\left(G\right)=A_{ℂ}\left(H\right)+B$, where $B$ is the matrix with $b_{ij}=\frac{1}{2}(1+i)$, $b_{ji}=\frac{1}{2}(1-i)$ and all other entries zero. Since $B$ has exactly one positive eigenvalue and exactly one negative eigenvalue, the result follows by applying Weyl’s theorem [3].□

Lemma 5

Let $G$ be a multidigraph on $n+1$ vertices and $H$ be obtained by deleting one vertex from $G$ . If ${\lambda }_1\left(G\right)\le {\lambda }_2\left(G\right)\le \cdots \le {\lambda }_{n+1}\left(G\right)$ are the $A_{ℂ}$ -eigenvalues of $G$ written in nondecreasing order and ${\lambda }_1\left(H\right)\le {\lambda }_2\left(H\right)\le \cdots \le {\lambda }_n\left(H\right)$ are the $A_{ℂ}$ -eigenvalues of $H$ written in nondecreasing order, then $${\lambda }_1\left(G\right)\le {\lambda }_1\left(H\right)\le {\lambda }_2\left(G\right)\le \cdots \le {\lambda }_n\left(G\right)\le {\lambda }_n\left(H\right)\le {\lambda }_{n+1}\left(G\right).$$

Proof

Observe that $A_{ℂ}\left(H\right)$ is a principal submatrix of $A_{ℂ}\left(G\right)$. In particular, $$A_{ℂ}\left(G\right)=\left[\begin{array}{cc}\hfill A_{ℂ}\left(H\right)\hfill & \hfill y\hfill \\ \hfill y^{\ast }\hfill & \hfill 0\hfill \end{array}\right],$$for some vector $y\in {ℂ}^n$. Now using Cauchy’s interlacing theorem [3], the result follows immediately.□

The above lemma ensures that if $\lambda$ is an $A_{ℂ}$-eigenvalue of the multidigraph $G$ with multiplicity at least $2$, then $\lambda$ is also an $A_{ℂ}$-eigenvalue of $H$ with multiplicity at least $1$.

To avoid drawing several arcs between a pair of vertices in a multidigraph, we use the following alternative. Take the underlying undirected simple graph of the multidigraph and give an arbitrary orientation to each of its edges. If in the new (oriented) graph, there is a directed edge from vertex $i$ towards vertex $j$, then assign that edge with weight equal to the $ij$th component of the complex adjacency matrix of that multidigraph.

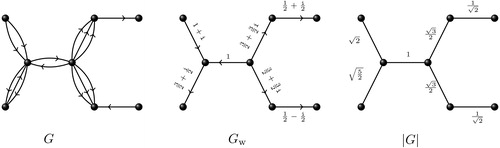
So in this way, we draw a weighted directed graph in place of a multidigraph, where the weights are complex numbers belonging to the set ${\mathbb{W}}_{+}=\left\{\frac{a}{2}+\frac{b}{2}i:a,b\in \mathbb{Z},a\ge \left|b\right|\ge 0\text{and}2|(a-b)\right\}\setminus \left\{0\right\}$. If $G$ is a multidigraph, then $G_{\mathrm{u}}$ and $G_{\mathrm{w}}$ denote its underlying undirected simple graph and associated weighted directed graph, respectively. Fig. 2 shows a multidigraph, its underlying undirected simple graph and the associated weighted directed graph.

Fig. 2 A multidigraph $G$, its underlying undirected simple graph $G_{\mathrm{u}}$ and associated weighted directed graph $G_{\mathrm{w}}$.

Remark 6

Note that, in the above process, if we fix the orientation of the edges of $G_{\mathrm{w}}$ in the following way, then we can get a unique weighted mixed graph associated with the multidigraph. For any edge $\{i,j\}$ in the underlying weighted graph, give an orientation from $i$ to $j$ (from $j$ to $i$) if the imaginary part of the $ij$th entry is positive (negative) and keep the edge $\{i,j\}$ as undirected if the $ij$th entry is real and positive.

Notice that, in this way, we can always associate a weighted digraph with a multidigraph such that the complex adjacency matrix of a multidigraph is same as the adjacency matrix of the associated weighted digraph. In the past decade, the spectral properties of complex weighted digraphs have been studied. In [7], Bapat, Kalita and Pati introduced the adjacency matrix for a weighted digraph with complex weights of unit modulus. Later, Kalita [8] gave a characterization of the unicyclic weighted digraphs $G$ with weights from the set $\{\pm 1,\pm i\}$ whose adjacency matrix $A\left(G\right)$ satisfies property (SR), i.e., “if $\lambda$ is an eigenvalue of $A\left(G\right)$, then $\frac{1}{\lambda }$ is also an eigenvalue of $A\left(G\right)$ with the same multiplicity”. Recently, Sahoo [9] considered complex adjacency matrix of a digraph and showed that not only its eigenvalues but also its eigenvectors carry a lot of information about the structure of the digraph.

We emphasize here that an undirected simple graph $H$ can be viewed as a multidigraph $G$. In that case, the adjacency matrix $A\left(H\right)$ is same as the complex adjacency matrix $A_{ℂ}\left(G\right)$. Hence, we may view the study of complex adjacency spectrum of a multidigraph as a general activity.

We write $i\stackrel{w}{⟶}j$ to mean that there are $\text{Re}\left(w\right)+\text{Im}\left(w\right)$ directed edges from $i$ to $j$ and $\text{Re}\left(w\right)-\text{Im}\left(w\right)$ directed edges from $j$ to $i$ in the multidigraph $G$. In this case, if $w\in {\mathbb{W}}_{+}$, then the vertices $i$ and $j$ in $G$ are called adjacent; otherwise they are nonadjacent. A multidigraph $G$ is said to be bipartite multidigraph if its underlying undirected simple graph is bipartite. Similarly, we can define a multi-directed tree, a path multidigraph, a star multidigraph, etc. Let $G$ be a multidigraph on vertices $1,2,\dots ,n$. Then the modular graph of $G$, denoted by $\left|G\right|$, is the weighted undirected graph obtained from $G_{\mathrm{w}}$ by replacing each of its edge weights by their modulus.

In this article, we supply some results on the complex adjacency spectra of multidigraphs. In Section 2, we compute the complex adjacency spectra of some special class of bipartite multidigraphs. It is well known that a simple undirected connected graph is bipartite if and only if its adjacency spectrum is symmetric about the origin (with multiplicity). We show that the result is not true, in general, for multidigraphs with respect to complex adjacency spectrum and supply a class of non-bipartite multidigraphs which have this property. In Section 3, we describe the complete $A_{ℂ}$-spectra of some special multi-directed trees. Further, given any multi-directed tree $T$, we prove that if we change the direction of any edge in the associated weighted tree $T_{\mathrm{w}}$ (that is, if we replace $i\stackrel{w}{⟶}j$ by $i\stackrel{\overline{w}}{⟶}j$ for two adjacent vertices $i$ and $j$) then the complete $A_{ℂ}$-spectrum of the corresponding new multi-directed tree remains unchanged. Furthermore, we prove that a multi-directed tree $T$ and its modular tree $\left|T\right|$ share the same $A_{ℂ}$-spectrum.

Following notations are being used in the rest of the paper. The $n\times 1$ vector with each entry $1$ (respectively, $0$) is denoted by ${\mathbf{1}}_n$ (respectively, ${\mathbf{0}}_n$). $M_n$ denotes the set of complex matrices of order $n$. By $I_n$, we denote the identity matrix of size $n$. For $z\in ℂ$, the set of all complex numbers, $\overline{z}$, $arg\left(z\right)$ and $\left|z\right|$ represent the conjugate, the argument and the modulus of $z$. We choose $arg\left(0\right)=0$, as a convention. By $x={\left(x_i\right)}_{i=1}^n$, we mean a column vector of length $n$. A vector, whose $i$th and the $j$th components are $1$ and $-1$, respectively and rest all components are $0$, is denoted by ${ϵ}_{i,j}$. The Euclidean norm of $x$ is denoted by $\Vert x\Vert$, while the Euclidean inner product of two vectors $x,y$ is denoted by $〈x,y〉$. The transpose and conjugate transpose of a matrix $A$ are denoted by $A^T$ and $A^{\ast }$, respectively.

2 $A_{ℂ}$–Spectra of bipartite multidigraphs

Note that, if $A=\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill B\hfill \\ \hfill B^{\ast }\hfill & \hfill \mathbf{0}\hfill \end{array}\right]$ is a square matrix and $x=\left(\begin{array}{c}\hfill x^{\left(1\right)}\hfill \\ \hfill x^{\left(2\right)}\hfill \end{array}\right)$ is an eigenvector for an eigenvalue $\lambda$, then $\hat{x}=\left(\begin{array}{c}\hfill -x^{\left(1\right)}\hfill \\ \hfill x^{\left(2\right)}\hfill \end{array}\right)$ is an eigenvector of $A$ for the eigenvalue $-\lambda$. In fact, if $x_1,\dots ,x_k$ are $k$ linearly independent eigenvectors of $A$, then ${\hat{x}}_1,\dots ,{\hat{x}}_k$ are also linearly independent. That is, the eigenvalues of $A$ are symmetric about the origin.

The complex adjacency matrix of a bipartite multidigraph $G$ has the above mentioned form and hence its $A_{ℂ}$-eigenvalues are symmetric about the origin. We say a multidigraph $G$ satisfies SO-property if the $A_{ℂ}$-spectrum of $G$ is symmetric about origin. Note that the converse of this is true for connected undirected graphs. But, in the case of multidigraphs it is not true in general. See the following example.

Example 7

Consider the multidigraph $G$ as shown in Fig. 3. One can check that the characteristic polynomial of $A_{ℂ}\left(G\right)$ is $$\varphi (A_{ℂ}\left(G\right),x)=x\left(x^2-\frac{7+3\sqrt{2}}{2}\right)\left(x^2-\frac{7-3\sqrt{2}}{2}\right).$$Thus the $A_{ℂ}$-spectrum of $G$ is symmetric about origin but $G$ is not bipartite (since its underlying undirected simple graph is a cycle on odd number of vertices).

Fig. 3 A non-bipartite multidigraph $G$ whose $A_{ℂ}$-spectrum is symmetric about origin and $G_{\mathrm{w}}$, the corresponding associated weighted cycle digraph.

Now, a natural question that arise here is “which non-bipartite multidigraphs satisfy the SO-property?”. Here we provide a class of non-bipartite multidigraphs with SO-property.

Let $G$ be a cycle multidigraph with vertices $1,\dots ,n$ and with the associated weighted digraph $G_{\mathrm{w}}$. If $i\stackrel{w_i}{⟶}(i+1)$ for $i=1,\dots ,n-1$ and $n\stackrel{w_n}{⟶}1$ in $G_{\mathrm{w}}$ and no other vertices are adjacent, then we denote the cycle multidigraph $G$ by $C_n\left(w\right)$, where $w={\left(w_i\right)}_{i=1}^n$. Depending on whether the number of vertices of a cycle multidigraph is odd or even, it can be categorized as odd or even cycle multidigraph. Since the even cycle multidigraphs are bipartite, hence they satisfy SO-property. To find out which odd cycle multidigraphs satisfy SO-property, we consider weight of a cycle multidigraph which is defined as the product of weights of all the directed edges of the associated weighted proper cycle digraph. (Note: A proper cycle digraph is a cycle digraph such that each of its directed edges are oriented either clockwise or anticlockwise.) Notice that the weight of the cycle multidigraph as shown in Fig. 3 is $\frac{5i}{4}$. The following theorem supplies a necessary and sufficient condition under which an odd cycle multidigraph satisfies SO-property.

Theorem 8

Let $G=C_n\left(w\right)$ be an odd cycle multidigraph on $n$ vertices, where $w={\left(w_i\right)}_{i=1}^n\in {\mathbb{W}}_{+}^n$ . Then the weight of $G$ is purely imaginary if and only if $G$ satisfies SO-property.

Proof

The complex adjacency matrix of $G$ can be expressed as $$A_{ℂ}\left(G\right)=\left[\begin{array}{cccccc}\hfill 0\hfill & \hfill w_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\overline{w}}_n\hfill \\ \hfill {\overline{w}}_1\hfill & \hfill 0\hfill & \hfill w_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\overline{w}}_2\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill w_{n-1}\hfill \\ \hfill w_n\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\overline{w}}_{n-1}\hfill & \hfill 0\hfill \end{array}\right].$$Let the characteristic polynomial of $A_{ℂ}\left(G\right)$ be given by $$\varphi (A_{ℂ}\left(G\right),x)=x^n+a_{n-1}{x}^{n-1}+\cdots +a_2{x}^2+a_{1}x+a_0.$$Now, suppose $w_1{w}_2\dots w_n=a+bi$, where $a,b\in \mathbb{R}$. Then $a_0=det\left(A_{ℂ}\left(G\right)\right)=w_1{w}_2\dots w_n+{\overline{w}}_1{\overline{w}}_2\dots {\overline{w}}_n=a+bi+a-bi=2a$. Hence, $a_0=0$ if and only if $a=0$. Furthermore, observe that all the principal minors of odd orders are zero. Therefore, the characteristic polynomial of $A_{ℂ}\left(G\right)$ becomes $$\varphi (A_{ℂ}\left(G\right),x)=x^n+a_{n-2}{x}^{n-2}+\cdots +a_3{x}^3+a_{1}x.$$Hence the result follows.□

Let $G=(V,E)$ be a multidigraph and $G_1=(V_1,E_1)$ be such that $V_1\subset V$, $E_1\subset E$. For $i,j\in V_1$, if $i\stackrel{w}{⟶}j$ in $G_1$ for $w\in {\mathbb{W}}_{+}$ implies $i\stackrel{w}{⟶}j$ in $G$, then we call $G_1$ as a sub-multidigraph of $G$. Let us call a multidigraph in which weights of all odd cycle sub-multidigraphs are purely imaginary as an im-bipartite multidigraph. Thus, all bipartite multidigraphs are also im-bipartite. The following theorem gives a further sufficient condition for the $A_{ℂ}$-spectrum of a multidigraph to be symmetric about the origin.

Theorem 9

An im-bipartite multidigraph satisfies SO-property.

Proof

Let $G$ be an im-bipartite multidigraph on vertices $1,2,\dots ,n$. Let $p\le n$ be an odd number and $B=\left[b_{ij}\right]$ be the principal submatrix of $A_{ℂ}\left(G\right)$ corresponding to $\{1,2,\dots ,p\}$. From Leibniz’s formula for the determinant of a matrix, we have $$det\left(B\right)=\sum _{\varsigma \in {\mathfrak{S}}_p}\text{sgn}\left(\varsigma \right)\prod _{i=1}^p{b}_{i{\varsigma }_i},$$where ${\mathfrak{S}}_p$ is the permutation group of $\{1,\dots ,p\}$ and ${\varsigma }_i=\varsigma \left(i\right)$. Since $p$ is odd, thus $\varsigma \in {\mathfrak{S}}_p$ is a product of disjoint cycles of which at least one must be odd. Select an odd cycle $O$ that contains the smallest possible label from $\{1,2,\dots ,p\}$. Now consider the permutation, ${\varsigma }^{\prime }$ obtained from $\varsigma$, by replacing $O$ with its inverse $O^{-1}$. Using the hypothesis, the total contribution of $\varsigma$ and ${\varsigma }^{\prime }$ towards $detB$ is $$\text{(weight of}O\text{+ weight of}{O}^{-1}\text{)}\prod \text{weight of other cycles}=0,$$as the weight of $O$ is purely imaginary. Hence $det\left(B\right)=0$. With a similar argument one can observe that the determinant of any principal submatrix of order $p$ is zero. It follows that, the coefficient of $x^{n-p}$ in the characteristic polynomial of $A$, is zero.□

Next we consider some special types of bipartite multidigraphs and characterize their $A_{ℂ}$-spectrum. In the case of undirected bipartite graphs, we have a special class of graphs called the complete bipartite graphs. The adjacency spectrum of a complete bipartite graph contains exactly two nonzero eigenvalues which can be obtained easily from the number of vertices in each part. Motivated by this, we define below some special classes of bipartite multidigraphs and obtain their $A_{ℂ}$-spectra .

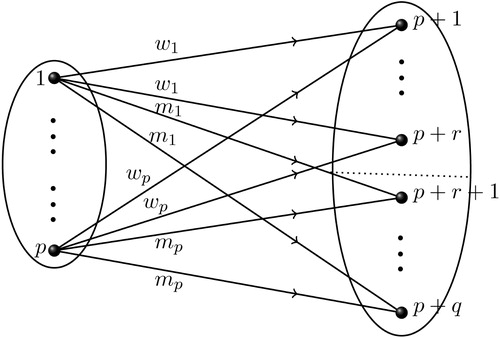
Let $w=\left(w_i\right),m=\left(m_i\right)\in {\mathbb{W}}_{+}^p$. Consider a bipartite multidigraph $G$ with $V_1=\{1,2,\dots ,p\}$ and $V_2=\{p+1,p+2,\dots ,p+q\}$ as its disjoint vertex set partition. If $i\stackrel{w_i}{⟶}j$ for all $i\in V_1$ and $j\in V_2$, then we call $G$ a type-I bipartite multidigraph and denote by $K_{p,q}\left(w\right)$. If $w_1=\cdots =w_p=\alpha$, then we call $G$ as a semi-regular bipartite multidigraph and denote by $\alpha$-$K_{p,q}$.

Further, if $V_2$ is again partitioned into two disjoint sets $S$ and $T$ with $\left|S\right|=r$ and if $i\stackrel{w_i}{⟶}j$ for $i\in V_1,j\in S$ and $i\stackrel{m_i}{⟶}j$ for $i\in V_1,j\in T$, then we call $G$ a type-II bipartite multidigraph and denote it by $K_{p,q}^r(w,m)$. Fig. 4 shows the associated weighted digraph of $K_{p,q}^r(w,m)$.

Fig. 4 The associated weighted digraph of a type-$2$ bipartite multidigraph $K_{p,q}^r(w,m)$.

Our next theorem describes the $A_{ℂ}$-spectrum of type-II bipartite multidigraph.

Theorem 10

Let $G=K_{p,q}^r(w,m)$ be a type-II bipartite multidigraph as described above. Then the $A_{ℂ}$ -spectrum of $G$ consists of

(i)	$0$ with multiplicity $p+q-4$ ,
(ii)	$\pm \sqrt{\frac{r\Vert w{\Vert }^2+(q-r)\Vert m{\Vert }^2\pm \sqrt{{(r\Vert w{\Vert }^2-(q-r)\Vert m{\Vert }^2)}^2+4r(q-r)〈w,m〉〈m,w〉}}{2}}$ each with multiplicity $1$ .

Proof

Consider the $p\times q$ matrix $B=\left[\begin{array}{cccccc}\hfill w\hfill & \hfill \cdots \hfill & \hfill w\hfill & \hfill m\hfill & \hfill \cdots \hfill & \hfill m\hfill \end{array}\right]$, with the first $r$ columns as vector $w$ and the rest $q-r$ columns as vector $m$. Then the adjacency matrix of $G$ can be expressed as $A=\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill B\hfill \\ \hfill B^{\ast }\hfill & \hfill \mathbf{0}\hfill \end{array}\right]$. Since $w,m\in {\mathbb{W}}_{+}^p$, there are at least $p-2$ linearly independent vectors say, $x_1,x_2,\dots ,x_{p-2}$ in ${\mathbb{W}}^p$, which are orthogonal to both $w$ and $m$. Now, consider the following $p+q-4$ linearly independent vectors $$\left(\begin{array}{c}\hfill {\mathbf{0}}_p\hfill \\ \hfill {ϵ}_{1,j}\hfill \\ \hfill {\mathbf{0}}_{q-r}\hfill \end{array}\right),\left(\begin{array}{c}\hfill {\mathbf{0}}_p\hfill \\ \hfill {\mathbf{0}}_r\hfill \\ \hfill {ϵ}_{1,k}\hfill \end{array}\right),\text{and}\left(\begin{array}{c}\hfill x_l\hfill \\ \hfill {\mathbf{0}}_r\hfill \\ \hfill {\mathbf{0}}_{q-r}\hfill \end{array}\right),$$for $j=2,3,\dots ,r;k=2,3,\dots ,q-r;l=1,2,\dots ,p-2$. Observe that $0$ is one eigenvalue of $A$ afforded by these $p+q-4$ eigenvectors.

Looking at the structure of the matrix $A$, let us consider a vector $v$ of the form $$v=\left(\begin{array}{c}\hfill k_1(w+m)\hfill \\ \hfill k_2{\mathbf{1}}_r\hfill \\ \hfill {\mathbf{1}}_{q-r}\hfill \end{array}\right),\text{where}{k}_1\text{and}{k}_2\text{are some constants}.$$Note that $v$ is orthogonal to the $p+q-4$ vectors mentioned above. Now, if $v$ is an eigenvector of $A$ corresponding to the eigenvalue $\lambda$ (say), then $v$ must satisfy the equation $Av=\lambda v$.

Now from the matrix equation, we get (1) $$k_{2}n{w}_i+(q-n)m_i=k_1(w_i+m_i)\lambda \text{for}i=1,\dots ,p;$$(1) (2) $$k_1\sum _{i=1}^p(w_i+m_i){\overline{w}}_i=k_2\lambda ;$$(2) (3) $$k_1\sum _{i=1}^p(w_i+m_i){\overline{m}}_i=\lambda ,$$(3) where $k_1,k_2$ and $\lambda$ are the unknowns.

Multiplying Eq. (1) by $w_i$ and $m_i$, separately, for $i=1,\dots ,p$, we have the following: (4) $$k_{2}n〈w,w〉+(q-n)〈m,w〉=k_1\lambda (〈w,w〉+〈m,w〉),$$(4) (5) $$k_{2}n〈w,m〉+(q-n)〈m,m〉=k_1\lambda (〈w,m〉+〈m,m〉).$$(5)

Further, Eqs. (2) and (3) can be restated as (6) $$k_1(〈w,w〉+〈m,w〉)=k_2\lambda ,$$(6) (7) $$k_1(〈w,m〉+〈m,m〉)=\lambda .$$(7)

Eliminating $k_1$, we get $$k_2{\lambda }^2=k_{2}r〈w,w〉+(q-r)〈m,w〉,{\lambda }^2=k_{2}r〈w,m〉+(q-r)〈m,m〉.$$Now eliminating $k_2$ from these two equations, we get an expression for $\lambda$ from which we can get the eigenvalues of $A$ and hence the result.□

By considering $r=q$, as an immediate corollary we get the following result which describes the $A_{ℂ}$-spectrum of a type-I bipartite multidigraph.

Corollary 11

Let $w=\left(w_i\right)\in {\mathbb{W}}_{+}^p$ . Then the $A_{ℂ}$ -spectrum of $K_{p,q}\left(w\right)$ consists of $0$ with multiplicity $p+q-2$ and $\pm \sqrt{q}\Vert w\Vert$ with multiplicity $1$ each. In particular, the spectrum of $\alpha$ - $K_{p,q}$ consists of $\pm \left|\alpha \right|\sqrt{pq}$ and $0$ with multiplicity $p+q-2$ .

Remark 12

Since each undirected edge between a pair of vertices can be considered as two oppositely oriented directed edges between those vertices, hence as a special case of Corollary 11 we get the spectrum of a complete bipartite undirected graph $K_{p,q}$. It consists of $\pm \sqrt{pq}$ and $0$ with multiplicity $p+q-2$.

3 Results on $A_{ℂ}$-spectra of multi-directed trees

This section contains results on the spectral properties of multi-directed trees.

A star multidigraph is a multidigraph whose underlying undirected simple graph is a star graph. Let $G$ be a star multidigraph on $n$ vertices with vertex $1$ as the central vertex. Let $w=\left(w_i\right)\in {\mathbb{W}}_{+}^{n-1}$. If $1\stackrel{w_i}{⟶}i$ for $i=1,\dots ,n-1$, then we denote $G$ by $S_n\left(w\right)$. If all the components of $w$ are equal, that is, $w_i=\alpha$ for all $i=1,\dots ,n-1$, then we call $S_n\left(w\right)$ as semiregular star multidigraph and denote by $\alpha$-$S_n$. The following corollary follows from Corollary 11 by considering $S_n\left(w\right)=K_{1,n-1}\left(w\right)$ which describes the complete $A_{ℂ}$-spectrum of a star multidigraph.

Corollary 13

Let $w=\left(w_i\right)\in {\mathbb{W}}_{+}^{n-1}$ . Let $S_n\left(w\right)$ be a star multidigraph with central vertex $1$ . Then the spectrum of $S_n\left(w\right)$ consists of $0$ with multiplicity $n-2$ and $\pm \Vert w\Vert$ with multiplicity $1$ each. More specifically, the spectrum of $\alpha$ - $S_n$ consists of $0$ with multiplicity $n-2$ and $\pm \left|\alpha \right|\sqrt{n-1}$ with multiplicity $1$ each.

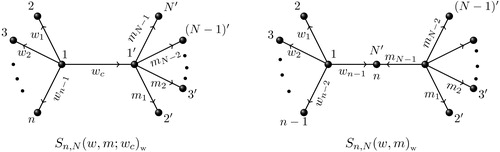
By a double star multidigraph, we mean a multidigraph $G$ for which $G_{\mathrm{u}}$ is a double star. Consider two star multidigraphs $S_n\left(w\right)$ and $S_N\left(m\right)$, where $w$ and $m$ are two vectors of length $n-1$ and $N-1$, respectively whose components belong to the set ${\mathbb{W}}_{+}$. Let $1$ and $1^{\prime }$ are the central vertices of $S_n\left(w\right)$ and $S_N\left(m\right)$, respectively. Let $w_c\in {\mathbb{W}}_{+}$. Then the multidigraph formed by joining the central vertices of $S_n\left(w\right)$ and $S_N\left(m\right)$ such that $1\stackrel{w_c}{⟶}{1}^{\prime }$, is known as a double star multidigraph and denoted by $S_{n,N}(w,m;w_c)$. Instead of joining the central vertices, if we merge a pendant vertex (say $n$) of $S_n\left(w\right)$ to a pendant vertex (say $N^{\prime }$) of $S_N\left(m\right)$, then the multidigraph thus produced is called a pendant-merge double star multidigraph and denoted by $S_{n,N}(w,m)$, see Fig. 5. Note that $S_{n,N}(w,m;w_c)$ and $S_{n,N}(w,m)$ have $n+N$ and $n+N-1$ number of vertices, respectively.

Fig. 5 The associated weighted digraphs of a double star multidigraph and a pendant-merge double star multidigraph.

Our next two results describe the $A_{ℂ}$-spectrum of a double star multidigraphs.

Theorem 14

Let $G=S_{n,N}(w,m;w_c)$ be a double star multidigraph. Then the $A_{ℂ}$ -spectrum of $G$ consists of

(i)	$0$ with multiplicity $n+N-4$ and
(ii)	$\pm \sqrt{\frac{{\left|w_c\right|}^2+\Vert w{\Vert }^2+\Vert m{\Vert }^2\pm \sqrt{{({\left|w_c\right|}^2+\Vert w{\Vert }^2+\Vert m{\Vert }^2)}^2-4\Vert w{\Vert }^2\Vert m{\Vert }^2}}{2}}$ each with multiplicity $1$ .

Proof

The complex adjacency matrix of $S_{n,N}(w,m;w_c)$ can be expressed as 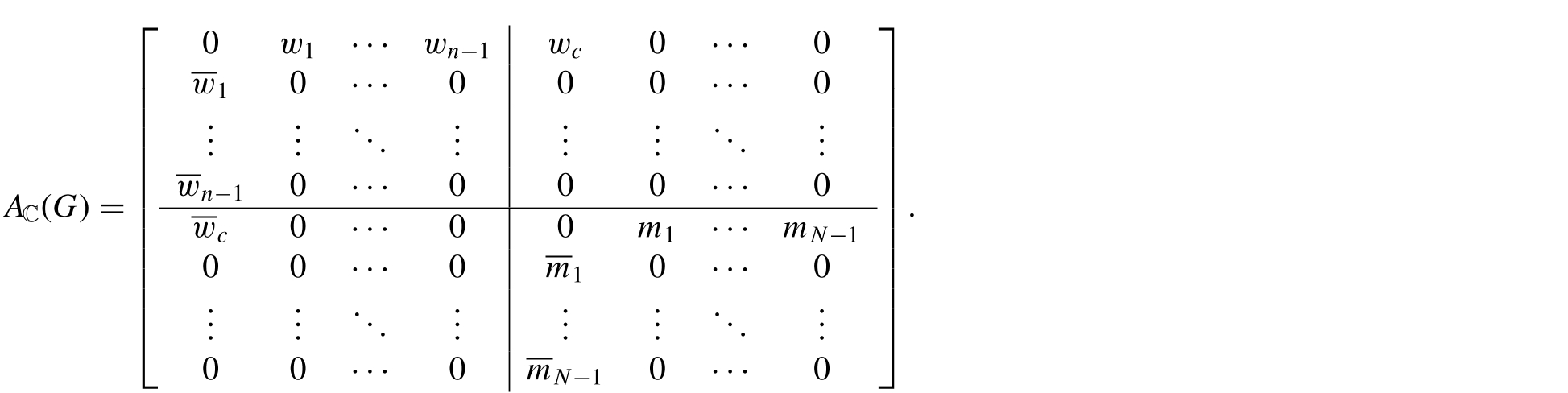Now, proof of part (i) is obvious by considering the nullity of $A_{ℂ}\left(G\right)$. To prove part (ii), consider the vector $$v={\left(\begin{array}{cccccccc}\hfill k_1\hfill & \hfill {\overline{w}}_1\hfill & \hfill \cdots \hfill & \hfill {\overline{w}}_{n-1}\hfill & \hfill k_2\hfill & \hfill k_3{\overline{m}}_1\hfill & \hfill \cdots \hfill & \hfill k_3{\overline{m}}_{N-1}\hfill \end{array}\right)}^T,$$where $k_1,k_2$ and $k_3$ are some constants. If $v$ happens to be an eigenvector corresponding to an eigenvalue $\lambda$ of $A_{ℂ}\left(G\right)$, then it must satisfy $A_{ℂ}\left(G\right)v=\lambda v$. From which we get $$\sum _{i=1}^{n-1}{w}_i{\overline{w}}_i+k_2{w}_c=k_1\lambda ,$$$$k_1{\overline{w}}_i={\overline{w}}_i\lambda ,\text{for}i=1,\dots ,n-1,$$$$k_1{w}_c+\sum _{i=1}^{N-1}{m}_i{\overline{m}}_i=k_2\lambda ,$$$$k_1{\overline{m}}_i=k_3{\overline{m}}_i\lambda ,\text{for}i=1,\dots ,N-1.$$ Now eliminating $k_1,k_2$ and $k_3$ from these equations, we have $${\lambda }^4-({\left|w_c\right|}^2+\Vert w{\Vert }^2+\Vert m{\Vert }^2){\lambda }^2+\Vert w{\Vert }^2\Vert m{\Vert }^2=0.$$Note that $\lambda \ne 0$ as $w$ and $m$ are nonzero vectors. Hence the result follows.□

The following result describes the complete spectrum of $S_{n,N}(w,m)$ in terms of $n,N$ and the norms of the weight vectors $w,m$.

Theorem 15

Let $w=\left(w_i\right)\in {\mathbb{W}}_{+}^{n-1},m=\left(m_i\right)\in {\mathbb{W}}_{+}^{N-1}$ . Let $G=S_{n,N}(w,m)$ be a pendant-merge double star multidigraph. If $\widehat{w}={(w_1,\dots ,w_{n-2})}^T,\widehat{m}={(m_1,\dots ,m_{N-2})}^T$ and $t=\left(\begin{array}{c}\hfill w\hfill \\ \hfill m\hfill \end{array}\right)$ , then the $A_{ℂ}$ -spectrum of $S_{n,N}(w,m)$ consists of

(i)	$0$ with multiplicity $n+N-5$ ,
(ii)	$\pm \sqrt{\frac{\Vert t{\Vert }^2\pm \sqrt{\Vert t{\Vert }^4-4({\left|w_{n-1}\right|}^2\Vert \widehat{w}{\Vert }^2+{\left|m_{N-1}\right|}^2\Vert \widehat{m}{\Vert }^2+\Vert \widehat{w}{\Vert }^2\Vert \widehat{m}{\Vert }^2)}}{2}}$ each with multiplicity $1$ .

Proof

The complex adjacency matrix of $G=S_{n,N}(w,m)$ can be expressed as Proof of part (i) is immediate by observing the nullity of $A_{ℂ}\left(G\right)$. To prove part (ii), consider a vector $v$ of the form ${\left(\begin{array}{ccccccccc}\hfill k_1\hfill & \hfill {\overline{w}}_1\hfill & \hfill \cdots \hfill & \hfill {\overline{w}}_{n-2}\hfill & \hfill k_2\hfill & \hfill k_3\hfill & \hfill k_4{\overline{m}}_1\hfill & \hfill \cdots \hfill & \hfill k_4{\overline{m}}_{N-2}\hfill \end{array}\right)}^T$, where $k_1,k_2,k_3$ and $k_4$ are some constants. If $v$ is an eigenvector of $A_{ℂ}\left(G\right)$ corresponding to an eigenvalue (say) $\lambda$, then from $A\left(G_{\mathrm{w}}\right)v=\lambda v$ we have the following equations: $$\Vert w{\Vert }^2+k_2{w}_n=k_1\lambda ,$$$$k_1=\lambda ,$$$$k_1{\overline{w}}_n+k_3{\overline{m}}_N=k_2\lambda ,$$$$k_4\Vert m{\Vert }^2+k_2{\overline{m}}_N=k_3\lambda ,$$$$k_3=k_4\lambda .$$ Eliminating $k_1,k_2,k_3$ and $k_4$ from the above system of equation, we get $${\lambda }^4-(\Vert w{\Vert }^2+\Vert m{\Vert }^2){\lambda }^2+{\left|w_n\right|}^2\Vert w{\Vert }^2+{\left|m_N\right|}^2\Vert m{\Vert }^2+\Vert w{\Vert }^2\Vert m{\Vert }^2=0.$$Note that $\lambda \ne 0$ as $w$ and $m$ are nonzero vectors. Hence the result follows.□

A path multidigraph is a multidigraph $G$ for which $G_{\mathrm{u}}$ is a path. Let $G$ be a path multidigraph on vertices $1,2,\dots ,n$. If $i\stackrel{w_i}{⟶}(i+1)$ for $i=1,\dots ,n-1$ in $G$ and $w=\left(w_i\right)\in {\mathbb{W}}_{+}^{n-1}$, then we denote $G$ by $P_n\left(w\right)$. If $w_1=\cdots =w_{n-1}=\alpha$, then we call the path multidigraph as the semi-regular path multidigraph and denote by $\alpha$-$P_n$. Since the complex adjacency matrix of a semi-regular path multidigraph is a tridiagonal Toeplitz matrix [10], we have the following immediate lemma.

Lemma 16

Let $\alpha$ - $P_n$ be a semi-regular path multidigraph on $n$ vertices. If $\alpha =r{e}^{i\theta }$ in polar form, then the $A_{ℂ}$ -spectrum of $\alpha$ - $P_n$ consists of $2rcos\left(\frac{j\pi }{n+1}\right)$ for $j=1,\dots ,n$ .

Next, we study the effect on the $A_{ℂ}$-spectrum of a multi-directed tree by reversing the orientation of any of its edge. The following is an important observation which is true for a more general class of multidigraphs.

Theorem 17

Let $G$ be a multidigraph on vertices $1,2,\dots ,n$ . Suppose that $i$ and $j$ be two vertices in $G$ such that $i\stackrel{w}{⟶}j$ , for some $w\in {\mathbb{W}}_{+}$ and by removing all the arcs between vertices $i$ and $j$ , $G$ becomes disconnected (that is, $i\stackrel{w}{⟶}j$ is a cut arc in $G_{\mathrm{w}}$ ). Let $H$ be the multidigraph obtained from $G$ by changing $i\stackrel{w}{⟶}j$ to $i\stackrel{\overline{w}}{⟶}j$ . Then $G$ and $H$ have the same $A_{ℂ}$ -spectra.

Proof

Suppose that $\lambda$ is an eigenvalue of $A_{ℂ}\left(G\right)$ with corresponding eigenvector $x={\left(x_k\right)}_{k=1}^n$. That is, $A_{ℂ}\left(G\right)x=\lambda x$. Since by deleting all the directed edges between $i$ and $j$ the multidigraph $G$ becomes disconnected, hence we get two components of $G$, say $G_1$ and $G_2$. Suppose that $i\in V\left(G_1\right)$ and $j\in V\left(G_2\right)$. Now choose such that . 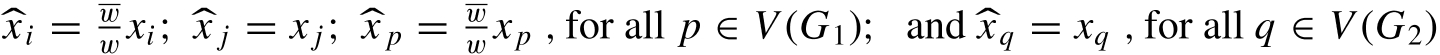Then it can be observed that is an eigenvector corresponding to the eigenvalue $\lambda$ of $A_{ℂ}\left(H\right)$. Hence the result follows.□

Since by deleting all the arcs between any two adjacent vertices of a multi-directed tree, the resulting multidigraph is disconnected, we have the following immediate corollary.

Corollary 18

Let $T$ be a multi-directed tree on vertices $1,\dots ,n$ . Let $i$ and $j$ be two adjacent vertices in $T$ such that $i\stackrel{w}{⟶}j$ , for some $w\in {\mathbb{W}}_{+}$ . Let $H$ be the multi-directed tree obtained from $T$ by changing $i\stackrel{w}{⟶}j$ to $i\stackrel{\overline{w}}{⟶}j$ . Then $T$ and $H$ have the same complex adjacency spectra.

Let $G$ be a multidigraph on vertices $1,2,\dots ,n$. Then the modular graph of $G$, denoted by $\left|G\right|$, is the weighted undirected simple graph obtained from $G_{\mathrm{w}}$ by replacing each of its edge weights by their modulus. That is, if $i\stackrel{w}{⟶}j$ in $G$ for some $w\in {\mathbb{W}}_{+}$, then the edge $\{i,j\}$ has weight $\left|w\right|$ in $\left|G\right|$. Observe that the adjacency matrix of $\left|G\right|$ is $A\left(\left|G\right|\right)=\left|A_{ℂ}\left(G\right)\right|$, where by $\left|A\right|$ we mean the entrywise modulus of a matrix $A$. See Fig. 6 for more clarification.

Fig. 6 Example of a multidigraph $G$, its weighted digraph $G_{\mathrm{w}}$ and corresponding modular graph $\left|G\right|$.

The following theorem gives a relationship between the $A_{ℂ}$-spectra of a multi-directed tree and its modular tree.

Theorem 19

Let $T$ be a multi-directed tree on $n$ vertices and $\left|T\right|$ be its modular tree. Let $A_{ℂ}\left(T\right)$ and $A\left(\left|T\right|\right)$ be the complex adjacency matrix and the adjacency matrix of $T$ and $\left|T\right|$ , respectively. Then both $T$ and $\left|T\right|$ share same $A_{ℂ}$ -spectrum, that is $${\sigma }_{A_{ℂ}}\left(T\right)={\sigma }_{A_{ℂ}}\left(\left|T\right|\right).$$ Furthermore, if $x$ and $y$ are eigenvectors of $A_{ℂ}\left(T\right)$ and $A\left(\left|T\right|\right)$ , respectively, corresponding to an eigenvalue $\lambda$ , then $\left|x\right|=\left|y\right|$ .

Proof

Let $y={\left(y_i\right)}_{i=1}^n$ be an eigenvector of $A\left(\left|T\right|\right)={\left[a_{ij}\right]}_{n\times n}$ corresponding to an eigenvalue $\lambda$. Now from the matrix equation $A\left(\left|T\right|\right)y=\lambda y$, we have $$\sum _{k=1}^n{a}_{ij}{y}_j=\lambda y_i\text{for}i=1,\dots ,n.$$Let $A_{ℂ}\left(T\right)={\left[c_{ij}\right]}_{n\times n}$. Notice that $\left|A_{ℂ}\left(T\right)\right|=A\left(\left|T\right|\right)=A_{ℂ}\left(\left|T\right|\right)$ where by $\left|A\right|$, we mean entry-wise modulus of a matrix $A$. Hence we have $a_{ij}=\left|c_{ij}\right|=c_{ij}{e}^{arg\left({\overline{c}}_{ij}\right)}$. Thus, $$\sum _{k=1}^n{c}_{ij}{y}_j{e}^{iarg\left({\overline{c}}_{ij}\right)}=\lambda y_i.$$Choose a vector $x={\left(x_i\right)}_{i=1}^n$ such that $\left|x\right|=\left|y\right|$ and for $i\stackrel{w}{⟶}j$ in $T$, $$x_j=\left\{\begin{array}{cc}\left|y_j\right|e^{i\theta },\hfill & \text{if}{y}_i{y}_j\ge 0\hfill \\ \left|y_j\right|e^{i(\theta +\pi )},\hfill & \text{otherwise}\hfill \end{array}\right.$$where $\theta =arg\left(x_i\right)+arg\left(\overline{w}\right)$ and $arg\left(x_1\right)=0$. This is possible, as there is no cycle sub-multidigraphs. Hence $x_j$, for $j=1,2,\dots ,n$, gets a unique valuation. Now, it is easy to observe that $x$ is an eigenvector of $A_{ℂ}\left(T\right)$ corresponding to the eigenvalue $\lambda$ and hence we are done.□

From the well known Perron–Frobenius theorem [11], we know that the spectral radius of a nonnegative irreducible matrix is simple and positive. Further, it tells that each component of the eigenvector corresponding to the largest eigenvalue, commonly known as Perron vector, is positive. Using this idea, we have the following immediate remark to state.

Remark 20

Since $A\left(\left|T\right|\right)$ is a nonnegative irreducible matrix of the modular graph $\left|T\right|$ of a multi-directed tree $T$, from Theorem 19, the largest eigenvalue of $A_{ℂ}\left(T\right)$ is simple and positive. Furthermore, if $x$ is an eigenvector of $A_{ℂ}\left(T\right)$ corresponding to its largest eigenvalue, then since $\left|\mathrm{Arg}\left(w\right)\right|\le \frac{\pi }{4}$ for any $w\in {\mathbb{W}}_{+}$, therefore the absolute values of the difference between the principal arguments of any two components of $x$ whose corresponding vertices are adjacent can never be greater than $\frac{\pi }{4}$.

Given any Hermitian matrix $A=\left[a_{ij}\right]$ of order $n\times n$ whose all diagonal entries are zero, we can associate with it a graph $G$ on $n$ vertices such that two vertices $i$ and $j$ are adjacent in $G$ if and only if $a_{ij}\ne 0$. The following theorem is one of our main results which gives a sufficient condition under which $A$ and $\left|A\right|$ have the same set of eigenvalues, where $A$ is a Hermitian matrix. The proof of the result is very similar to that of Theorem 19. Especially, from the proof of Theorem 19, notice that the values of the entries of $A_{ℂ}\left(T\right)$ do not play any role, rather the zero pattern present in this matrix accounts. Hence we have the following result which is the most important result of this section.

Theorem 21

Let $A$ be a Hermitian matrix of order $n\times n$ with all its diagonal entries zero such that its associated graph is a tree. Then $A$ and $\left|A\right|$ have the same set of eigenvalues. More generally, if $D$ is a real diagonal matrix of order $n\times n$ , then $D+A$ and $D+\left|A\right|$ also have the same set of eigenvalues.

Example 22

Let $$P=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill -\sqrt{2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\sqrt{2}\hfill & \hfill 3\hfill & \hfill 1-3i\hfill & \hfill 0\hfill & \hfill i\hfill \\ \hfill 0\hfill & \hfill 1+3i\hfill & \hfill -1\hfill & \hfill 0.5\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0.5\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -i\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1.8\hfill \end{array}\right].\text{So}\left|P\right|=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill \sqrt{2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \sqrt{2}\hfill & \hfill 3\hfill & \hfill \sqrt{10}\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill \sqrt{10}\hfill & \hfill -1\hfill & \hfill 0.5\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0.5\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1.8\hfill \end{array}\right].$$Notice that the matrix $P$ satisfies the condition given in Theorem 21. From computation through matlab, we get the spectra of $P$ and $\left|P\right|$ as $$\sigma \left(P\right)=\left(-3.0229,-0.2406,0.1424,1.6478,5.2734\right)=\sigma \left(\left|P\right|\right)$$which agrees with the result given in Theorem 21.

4 Conclusion

Even though associating a complex Hermitian matrix to a digraph is not new, the use of such matrices for a multidigraph is new to the literature. The real part of the complex adjacency matrix provides information about the total number of directed edges between any two vertices of a multidigraph, while the imaginary part gives the effective direction of any multi-directed edge.

In case of a multi-directed tree $T$, the complex adjacency spectrum of $T$ is same as the adjacency spectrum of its modular graph $\left|T\right|$. Besides, the eigenvectors of the complex adjacency matrix of $T$ specify the effective orientation of any multi-directed edge in $T$. Furthermore, we have got a class of Hermitian matrices for which the spectrum of a matrix in the class and the spectrum of the modulus (entrywise) of the matrix are the same.

We get a class of non-bipartite multidigraphs whose eigenvalues are symmetric about origin. In the process, we attempt to find the class of all Hermitian matrices whose eigenvalues are symmetric about origin. Here we get partial answers to this class of matrices.

Acknowledgments

The authorssincerely thank the reviewer for many valuable suggestions which improved the presentation of the article. The corresponding author acknowledges SERB, Government of India for financial support through grant (MTR/2017/000080). The second author acknowledges SERB, Government of India for financial support through grant (PDF/2018/000519).