Independent point-set dominating sets in graphs

Abstract

In this paper, we study graphs which possess an independent point-set dominating set (in short, ipsd-set). We call such a graph as an ipsd-graph. We first provide general structural characterization of separable ipsd-graphs and thereafter, in our quest to characterize such graphs, we establish that girth of an ipsd-graph is at most 5. We further characterize ipsd-graphs with girth 5 and $C_5$-free ipsd-graphs of girth 4. Then, we exhibit a class of ipsd-graphs with girth $g\left(G\right)=4$ containing $C_5$ as an induced subgraph and in the process, we introduce a new graph equivalence relation termed as duplicated equivalence.

Keywords:

• Domination
• Point-set domination
• Independent set
• Equivalence relation
• Duplicated equivalent

1 Introduction

For standard terminology and notation in graph theory, as also for pictorial representations of graphs, we refer the standard text-books such as F. Harary [1] and Chartrand [2]. For domination related concepts we refer the book by Haynes et al. [3,4]. Further, unless mentioned otherwise, graphs will be assumed to be finite and connected.

For any given graph $G=(V,E)$, we will denote the vertex set of $G$ by $V\left(G\right)$ (or simply $V$) and edge set of $G$ by $E\left(G\right)$ (or $E$). The neighborhood of a vertex $v$ in a graph $G$, denoted by $N_G\left(v\right)$, is the set of all vertices in $G$ adjacent with the vertex $v$. The set $N_G\left(v\right)\cup \left\{v\right\}$ is the closed neighborhood of vertex $v$ in $G$ and is denoted by $N_G\left[v\right]$. The distance $d_G(u,v)$ between two vertices $u$ and $v$ of graph $G$ is the length of shortest path joining them. The diameter of $G$ is given by $diam\left(G\right)=max\{d(u,v):u,v\in V\}$. A cycle of length $n$ will be called an $n$-cycle. If $G$ is a separable graph, then the set of all non-trivial blocks of $G$ will be denoted by ${\mathcal{B}}_G$.

E. Sampathkumar and Pushpa Latha [5] in 1993 defined a set $D\subseteq V$ to be a point-set dominating set (or in short psd-set) of graph $G$ if for every non-empty subset $S$ of $V\setminus D$ there exists a vertex $v\in D$ such that the induced subgraph $〈S\cup \left\{v\right\}〉$ is connected. This definition can be seen as a natural extension of the concept of domination (cf. [3,4]) by using the interpretation that a subset $D$ of the vertex set $V$ of $G$ is a dominating set if and only if for every singleton subset $\left\{s\right\}$ of $V\setminus D$, there exists a vertex $d$ in $D$ such that the induced subgraph $〈\left\{s\right\}\cup \left\{d\right\}〉$ is connected.

Though point-set domination as a concept was introduced purely from theoretical interest, it can be applied to many real life situations. One such real life context where the notion of point-set domination can be noticed is discussed in [6] when a set ($D$) of supervisors amongst the employees in a business organization ($V$) is needed to be identified so that each group ($W$) of workers amongst the rest ($V\setminus D$) forms a task group under the leadership of at least one of the supervisors (say $u$) irrespective of hierarchical relationships (adjacencies) existing within the group of workers—the task group so formed may be visualized as the set $W\cup \left\{u\right\}$. Obviously, this task group needs to be connected in order that each individual in the group be “relevant” in relation to others in the group towards its collective performance of the task(s).

Another motivation to study point-set domination is discussed in [7] which is inspired from the facility location application of domination (cf. [3]), where we want that for any chosen area (set of vertices) there should exist a station providing facility for the whole area.

Definition 1.1

A subset $D$ of the vertex set $V$ of graph $G$ is a point-set dominating set (or in short psd-set) of graph $G$ if for every non-empty subset $S$ of $V\setminus D$ there exists a vertex $v\in D$ such that the induced subgraph $〈S\cup \left\{v\right\}〉$ is connected.

Definition 1.2

[8] A set $I$ in a graph $G$ is an independent set if $〈I〉$ is totally disconnected. The independence number $\alpha \left(G\right)$ of $G$ is the maximum cardinality among all independent sets of G.

Note that some authors use ${\beta }_0\left(G\right)$ (cf. [9]) instead of $\alpha \left(G\right)$ to represent independence number.

Definition 1.3

A set $D$ in a graph $G$ is an independent point-set dominating set (or in short an ipsd-set) of graph $G$ if $D$ is independent and point-set dominating set of $G$.

In domination theory, by a well known result of Berge [10], every maximal independent set in a graph $G$ is an independent dominating set of $G$. Hence every finite graph has an independent dominating set. However, as noted in [5,6], a graph may or may not possess an independent point-set dominating set. Thus the study of graphs possessing an ipsd-set is an important problem in the theory of point-set domination in graphs.

Definition 1.4

A graph is said to be an ipsd-graph if it has an independent point-set dominating set (or psd-set), otherwise it will be referred to as a non-ipsd graph.

In [5], it was proved that there does not exist any independent psd-set in a graph with diameter greater than or equal to $5$.

Proposition 1.5

[5] If a connected graph $G$ possesses an independent psd-set, then its diameter does not exceed $4$ .

However, the condition is not sufficient and the cycle $C_6$ is such an example. The diameter of the cycle $C_6$ is $3$ and yet it does not possess an ipsd-set. Thus it is interesting to characterize graphs having independent psd-sets. The following are some useful results on ipsd-graphs.

Proposition 1.6

[5] Let $D$ be a psd-set of a graph $G$ and $u,v\in V\setminus D$ . Then $d(u,v)\le 2$ .

Proposition 1.7

[6] A graph $G$ has an independent psd-set if there exists a vertex $u\in V\left(G\right)$ such that $V\left(G\right)\setminus N\left(u\right)$ is independent.

Proposition 1.8

[6] If $G$ is a separable ipsd-graph and $D$ is an ipsd-set of $G$ such that $V\setminus D⊈B$ for every $B\in {\mathcal{B}}_G$ , then there exists a cut vertex $u\in V\left(G\right)$ such that $V\setminus D=N\left(w\right)$ . In particular, in this case $V\setminus N\left(w\right)$ is independent.

Theorem 1.9

[6] A tree $T$ has an independent psd-set if and only if $diam\left(T\right)\le 4$ .

Theorem 1.10

[6,11] Every independent point-set dominating set of a graph $G$ is a minimal point-set dominating set.

Acharya and Gupta [6,12] made an extensive study on the problem of determining graphs which possess an independent psd-set (or an ipsd-set). In particular, they studied structure of separable graphs admitting ipsd-sets by classifying the set ${\mathfrak{D}}_{ips}\left(G\right)$ of all independent psd-sets of a separable graph $G$ into three classes as follows: $${\mathfrak{D}}_{ips}(G;X)=\{D\in {\mathfrak{D}}_{ips}\left(G\right):\exists B\in {\mathcal{B}}_G\text{with}V\setminus D⊊V\left(B\right)\}$$$${\mathfrak{D}}_{ips}(G;Y)=\{D\in {\mathfrak{D}}_{ips}\left(G\right):\exists B\in {\mathcal{B}}_G\text{with}V\setminus D=V\left(B\right)\}$$$${\mathfrak{D}}_{ips}(G;Z)=\{D\in {\mathfrak{D}}_{ips}\left(G\right):V\setminus D\text{contains vertices of different blocks}\}.$$

For a separable graph $G$, if $D\in {\mathfrak{D}}_{ips}(G;X)$ and $B\in {\mathcal{B}}_G$ is such that $V\setminus D⊊V\left(B\right)$, then in [13], it was noted that $V\left(B\right)\cap D$ may or may not be an ipsd-set of $B$. On this basis, the set ${\mathfrak{D}}_{ips}(G;X)$ was further partitioned into two subclasses: $${\mathfrak{D}}_{ips}(G;X_1)≔\{D\in {\mathfrak{D}}_{ips}(G;X):V\left(B\right)\cap D\text{is an ipsd-set of}B\};$$$${\mathfrak{D}}_{ips}(G;X_2)≔\{D\in {\mathfrak{D}}_{ips}(G;X):V\left(B\right)\cap D\text{is not an ipsd-set of}B\}.$$

Thus $${\mathfrak{D}}_{ips}\left(G\right)={\mathfrak{D}}_{ips}(G;X_1)\cup {\mathfrak{D}}_{ips}(G;X_2)\cup {\mathfrak{D}}_{ips}(G;Y)\cup {\mathfrak{D}}_{ips}(G;Z).$$

Acharya and Gupta then obtained structural characterization of separable graphs admitting ipsd-set of each type separately.

Theorem 1.11

[6] For any separable graph $G$ with $\left|{\mathcal{B}}_G\right|\ge 1$ , ${\mathfrak{D}}_{ips}(G;X_1)\ne 0̸$ if and only if $\left|{\mathcal{B}}_G\right|=1$ and if ${\mathcal{B}}_G=\left\{B\right\}$ , then

1:	$B$ has independent psd-set $F$ and
2:	$V\left(G\right)\setminus V\left(B\right)$ consists of pendant vertices with their supports lying in $V\left(B\right)\setminus F$.

Theorem 1.12

[6] For any separable graph $G$ , ${\mathfrak{D}}_{ips}(G;X_2)\ne 0̸$ if and only if $\left|{\mathcal{B}}_G\right|=1$ and if ${\mathcal{B}}_G=\left\{B\right\}$ , then $V\left(B\right)$ can be partitioned into three non-empty subsets $V_1,V_2$ and $V_3$ satisfying following properties:

1:	$〈V_1〉$ is complete and for each $x\in V_1$ one has $N\left(x\right)\cap V_2=V_2$ , $N\left(x\right)\cap V_3=0̸$ and $N\left(x\right)\cap (V\left(G\right)\setminus V\left(B\right))\ne 0̸$ ;
2:	$V_3$ is an independent psd-set of $〈V_2\cup V_3〉$ and
3:	$V\left(G\right)\setminus V\left(B\right)$ consists of pendant vertices with their supports lying in the set $V\left(B\right)\setminus V_3=V_1\cup V_2$ .

Theorem 1.13

[6] For any separable graph $G$ , ${\mathfrak{D}}_{ips}(G;Y)\ne 0̸$ if and only if $\left|{\mathcal{B}}_G\right|=1$ and if ${\mathcal{B}}_G=\left\{B\right\}$ , then

1:	$〈V\left(B\right)〉$ is complete and ;
2:	for each $x\in V\left(B\right)$ , $N\left(x\right)\cap (V\left(G\right)\setminus V\left(B\right))\ne 0̸$ and consists of pendant vertices only.

Theorem 1.14

[6] For any separable graph $G$ with $\left|{\mathcal{B}}_G\right|\ge 1$ , ${\mathfrak{D}}_{ips}(G;Z)\ne 0̸$ if and only if there exists a cut vertex $w$ in $G$ such that

1:	$d(w,V\left(G\right))\le 2$ ,
2:	$V\left(B\right)\setminus N\left(w\right)$ is an ipsd-set of $B$ for every $B\in {\mathcal{B}}_G$ and
3:	if $\left|{\mathcal{B}}_G\right|\ge 2$ , then ${\bigcap }_{B\in {\mathcal{B}}_G}V\left(B\right)=\left\{w\right\}$ .

These theorems provide structural information of separable graphs possessing ipsd-sets. But, in general, the problem of characterizing graphs containing independent psd-sets is still open. In fact, it was noted by Acharya and Gupta in [6] that characterizing an ipsd-graph containing a triangle and/or pentagon is one of the most important unsolved problems in this area of the theory of domination in graphs.

Further, since any graph $G$ can be embedded as an induced subgraph into a graph containing independent psd-sets by adding a new vertex in $G$ adjacent to all the vertices of $G$, it is not possible to obtain a necessary and sufficient condition involving forbidden subgraphs that characterizes graphs containing an independent psd-set.

In this paper, we extend the work done by Acharya et al. in [6,11–17] on point-set domination, in particular, the work in [6] by focusing on the girth and circumference of ipsd-graphs.

The following observations on the distance of vertices in an ipsd-graph will be useful for further study on ipsd-graphs.

Observation 1.15

Let $D$ be an ipsd-set of a graph $G$ and $u,v\in V\left(G\right)$ be any two vertices.

(a)	If $u,v\in V\setminus D$ , then $d(u,v)\le 2$ .
(b)	If $d(u,v)=3$ , then at least one of $u$ and $v$ is in $D$ .
(c)	If $d(u,v)=4$ , then both $u$ and $v$ are in $D$ .
(d)	If $\mathcal{M}=\{u\in V\left(G\right):d(u,v)=4\text{for some}v\in V\left(G\right)\}$ , then $\mathcal{M}\subseteq D$.

Since our focus is on girths of ipsd-graphs, the following result due to Min-Jen Jou [8] will be helpful.

Theorem 1.16

[8] For cycle $C_n$ with $n\ge 3$ , $$\alpha \left(C_n\right)=\lfloor \frac{n}{2}\rfloor .$$

2 General results on IPSD graphs

In this section, we proceed with our investigation on graphs possessing an independent point-set dominating set (in short, ipsd-set). We first provide general structural characterization of separable ipsd-graphs.

Theorem 2.1

Let $G$ be a separable graph with $\left|{\mathcal{B}}_G\right|\ge 1$ . Then $G$ is an ipsd-graph if and only if exactly one of the following two conditions hold:

(i)

$\left|{\mathcal{B}}_G\right|=1$ and if ${\mathcal{B}}_G=\left\{B\right\}$ , then one of the following holds (a) $B$ has an ipsd-set $F$ and $V\left(G\right)\setminus V\left(B\right)$ consists of pendant vertices with their supports lying in $V\left(B\right)\setminus F$ (b) there exists a cut vertex $w$ in $G$ such that $V\left(B\right)\setminus N\left(w\right)$ is an ipsd-set of $B$ and $V\left(G\right)=N\left(N\left[w\right]\right)$ .

(ii)

$\left|{\mathcal{B}}_G\right|\ge 2$ and there exists a cut vertex $w$ in $G$ such that (a) ${\cap }_{B\in {\mathcal{B}}_G}V\left(B\right)=\left\{w\right\}$ , (b) $V\left(G\right)=N\left(N\left[w\right]\right)$ and (c) $V\left(B\right)\setminus N\left(w\right)$ is an ipsd-set of $B$ for every $B\in {\mathcal{B}}_G$ .

Proof

Let $G$ be an ipsd-graph and $D$ be an ipsd-set of $G$. We have three cases:

Case I. $V\setminus D⊊B$ for some $B\in {\mathcal{B}}_G$.

Then $\left|{\mathcal{B}}_G\right|=1$ and $D\in {\mathfrak{D}}_{ips}(G;X)$. If $D\in {\mathfrak{D}}_{ips}(G;X_1)$, then condition (i)(a) follows from Theorem 1.11 and we are done.

If $D\in {\mathfrak{D}}_{ips}(G;X_2)$, then ${\mathcal{B}}_G=\left\{B\right\}$ and $V\left(B\right)$ can be partitioned into three non-empty subsets $V_1,V_2$ and $V_3$ satisfying the conditions of Theorem 1.12. Then any vertex $w\in V_1$ is a cut vertex in $G$ and satisfies (i) (b).

Case II. $V\setminus D=B$ for some $B\in {\mathcal{B}}_G$.

Then $D\in {\mathfrak{D}}_{ips}(G;Y)$. From Theorem 1.13, ${\mathcal{B}}_G=\left\{B\right\}$ and

A	$〈V\left(B\right)〉$ is complete and ;
B	for each $x\in V\left(B\right)$, $N\left(x\right)\cap (V\left(G\right)\setminus V\left(B\right))\ne 0̸$ and consists of pendant vertices only.

Then it is easy to see that any vertex $w\in V\left(B\right)$, satisfies the condition (i)(b).

Case III. $V\setminus D$ contains vertices of different blocks.

Then $D\in {\mathfrak{D}}_{ips}(G;Z)$. From Theorem 1.14, if $\left|{\mathcal{B}}_G\right|=1$, then (i)(b) is satisfied and if $\left|{\mathcal{B}}_G\right|\ge 2$ (ii) is satisfied.

Conversely, suppose either condition (i) or (ii) holds. If (i)(a) is satisfied, then $F\cup (V\left(G\right)\setminus V\left(B\right))$ forms an ipsd-set of $G$. If (i)(b) or (ii) is satisfied, then $V\left(G\right)\setminus N\left(w\right)$ forms an ipsd-set of $G$. Thus in either case $G$ is an ipsd-graph.□

Next is an immediate but important consequence of the above theorem.

Corollary 2.2

If $G$ is an ipsd separable graph, then every block of $G$ is an ipsd-block.

Proof

Follows immediately from Theorem 2.1(b).□

Another interesting result can be derived for triangle free separable ipsd-graphs having at least two non-trivial blocks from Theorem 2.1.

Corollary 2.3

If $G$ is a triangle free ipsd separable graph with $\left|{\mathcal{B}}_G\right|\ge 2$ , then $G$ is $C_5$ -free.

Proof

Since $\left|{\mathcal{B}}_G\right|\ge 2$, by Theorem 2.1, there exists a cut vertex $w$ such that $V\left(G\right)\setminus N\left(w\right)$ is an independent set in $G$. Suppose $G$ is not $C_5$-free graph, then there exists $B^{\ast }\in {\mathcal{B}}_G$ such that $C_5$ is an induced subgraph of $B^{\ast }$. As $G$ is triangle free, there exist adjacent vertices $u_1,u_2\in V\left(B^{\ast }\right)$ such that $d(u_i,w)\ge 2$ for $i=1,2$. Then $u_1,u_2\in V\left(G\right)\setminus N\left(w\right)$, a contradiction to the fact that $V\left(G\right)\setminus N\left(w\right)$ is an independent set. Thus $G$ is $C_5$-free.□

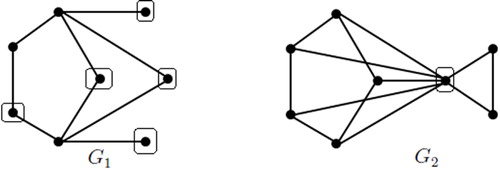
It is important to note that neither of the conditions i.e., being triangle free or having at least two non-trivial blocks can be dropped, otherwise separable ipsd-graph might fail to be $C_5$-free. For example the graphs $G_1$ and $G_2$ in Fig. 1 are both ipsd-graphs but fail to be $C_5$-free. The graph $G_1$ is triangle free but have a unique non-trivial block. While the graph $G_2$ has two non-trivial blocks but has $C_3$ as a subgraph.

Fig. 1 Ipsd-graphs $G_1$ and $G_2$.

Next, we proceed to prove that girth of an ipsd-graph is less than or equal to $5$.

Theorem 2.4

If $G$ is an ipsd graph, then $girth\left(G\right)\le 5$

Proof

Let $G$ be an ipsd-graph such that $girth\left(G\right)=k\ge 6$ and $D$ be an ipsd-set of $G$. Let $C$ be any $k$-cycle in $G$. From Theorem 1.16, $\alpha \left(C\right)=\lfloor k∕2\rfloor$, it follows that $|(V\setminus D)\cap V\left(C\right)|\ge 3$. If $|(V\setminus D)\cap V\left(C\right)|\ge 4$, then there exist vertices $u,v\in (V\setminus D)\cap V\left(C\right)$ such that $d_C(u,v)\ge 3$. As $D$ is an ipsd-set, there exists a vertex $x\in D\setminus V\left(C\right)$ such that $\{u,v\}\subseteq N\left(x\right)$ But then we get a cycle in $G$ of length less than or equal to $\lfloor k∕2\rfloor +2$, a contradiction to minimality of $C$. Thus $|(V\setminus D)\cap V\left(C\right)|=3$. Consequently, $|D\cap V\left(C\right)|=3$, $\left|V\left(C\right)\right|=6$ and $(V\setminus D)\cap V\left(C\right)$ is an independent subset of $V\left(C\right)$.

Since $(V\setminus D)\cap V\left(C\right)$ is independent, there exists $x^{\prime }\in D\setminus V\left(C\right)$ such that $(V\setminus D)\cap V\left(C\right)\subseteq N\left(x^{\prime }\right)$. But then $〈V\left(C\right)\cup x^{\prime }〉$ contains a $4$-cycle, again a contradiction to the minimality of $C$. Hence our assumption is wrong and $girth\left(G\right)\le 5$. □

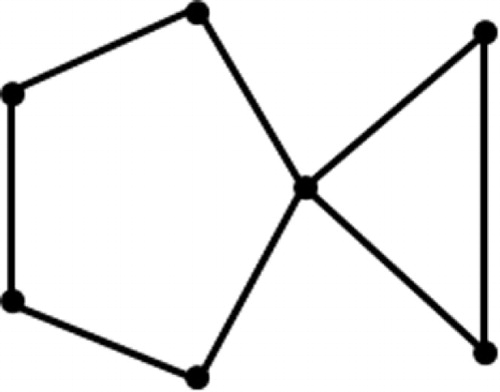
The condition in Theorem 2.4 is necessary but it is not sufficient. There exist graphs with girth less than or equal to $5$ that are not $ipsd$ graphs. In fact the graph in Fig. 2 is a graph with girth $3$

Fig. 2 Non-ipsd graph of girth $3$.

and yet is not an ipsd graph.

This result provides a new direction to the problem of characterizing ipsd-graphs. As trees are already characterized, the problem of characterizing ipsd-graphs narrows down to considering ipsd graphs of girth 3,4 and $5$, which we tackle in the sections to follow.

3 Classes of IPSD graphs

In this section, we characterize ipsd-graphs of girth $5$ and thereafter, present few classes of ipsd-graphs of girth $3$ and $4$. We first introduce following definition and notations.

Definition 3.1

[18] To subdivide an edge $e$ means to delete $e$, add a vertex $x$ and then join $x$ to the end vertices of $e$ (when $e$ is a link, this amounts to replacing $e$ by a path of length two). Any graph derived from a graph $G$ by a sequence of edge subdivisions is called a subdivision of $G$ or a $G$-subdivision.

Notation 3.2

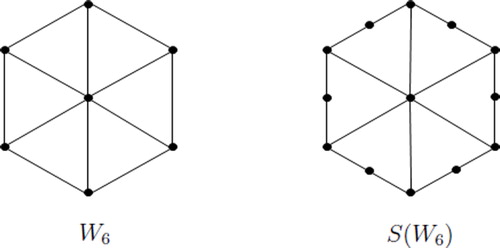
For any positive integer $n\ge 3$ , we denote by $S{K}_n$ , the graph obtained by subdividing each edge of a hamiltonian cycle of complete graph $K_n$ exactly once (see Fig. 3 ).

Fig. 3 Illustration of graphs $S{K}_n$ for $n=2,3$.

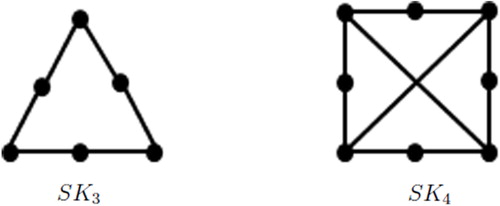
Theorem 3.3

A $2$ -connected graph $G$ with girth $5$ is an ipsd graph if and only if $G$ is isomorphic to either $C_5$ or $S{K}_4$ .

Proof

Let $G(\ncong C_5)$ be an ipsd-graph and $D$ be an ipsd set of $G$. Let $C=(v_1,v_2,v_3,v_4,v_5,v_1)$ be a $5$-cycle in $G$. Since $D$ is independent, $|D\cap V\left(C\right)|\le 2$.

Claim 1. $|D\cap V\left(C\right)|=2$.

If $|D\cap V\left(C\right)|=0$, then for $\{v_1,v_3\}\subset V\setminus D$, there exists $w\in D$ such that $\{v_1,v_3\}\subseteq N\left(w\right)$. Hence $〈\{v_1,v_2,v_3,w\}〉$ contains $4$-cycle, a contradiction. If $|D\cap V\left(C\right)|=1$, w.l.o.g we can assume that $D\cap V\left(C\right)=\left\{v_1\right\}$, then for the independent set $\{v_2,v_5\}$ in $V\setminus D$ there exists $w^{\prime }\in D$ such that $\{v_2,v_5\}\subseteq N\left(w^{\prime }\right)$. But, in that case, $〈\{v_1,v_2,w^{\prime },v_5\}〉$ contains either $C_3$ or $C_4$, a contradiction. Thus $|D\cap V\left(C\right)|=2$. Let $D\cap V\left(C\right)=\{v_1,v_4\}$.

Claim 2. $d\left(v_1\right)=d\left(v_4\right)=2$.

Suppose $d\left(v_1\right)\ge 3$ or $d\left(v_4\right)\ge 3$. W.l.o.g assume that $d\left(v_1\right)\ge 3$. Then there exists $z\in (N\left(v_1\right)\setminus V\left(C\right))\cap (V\setminus D)$. Since $D$ is an ipsd-set, for the independent set $\{z,v_3,v_5\}$ in $V\setminus D$, there exists $w\in D$ such that $\{z,v_3,v_5\}\subseteq N\left(w\right)$. Then $〈\{w,v_3,v_4,v_5\}〉\cong C_4$, a contradiction. Thus $d\left(v_1\right)=d\left(v_4\right)=2$.

Consequently, since $G\ncong C_5$, we must have $D\setminus V\left(C\right)\ne 0̸$ and $(V\setminus D)\setminus V\left(C\right)\ne 0̸$.

Claim 3. $|D\setminus V\left(C\right)|=2$ and $|(V\setminus D)\setminus V\left(C\right)|=1$.

First we show that $d\left(v\right)=2$ for each $v\in D\setminus V\left(C\right)$. Let, if possible, there exists $x\in D\setminus V\left(C\right)$ such that $d\left(x\right)\ge 3$. As girth of $G$ is $5$ and $v_4\in D$, $|N\left(x\right)\cap N\left(v_3\right)|=1$ and $|N\left(x\right)\cap N\left(v_5\right)|=1$. Then it is easy to see that there exists $z^{\ast }\in N\left(x\right)$ such that $\{z^{\ast },v_3,v_5\}$ is an independent set. Since $D$ is psd-set, there exists $w^{\ast }\in D\setminus V\left(C\right)$ such that $\{z^{\ast },v_3,v_5\}\subseteq N\left(w^{\ast }\right)$. Then $〈\{w^{\ast },v_3,v_4,v_5\}〉\cong C_4$, a contradiction. Thus $d\left(v\right)=2$ for each $v\in D\setminus V\left(C\right)$.

Next we show that $x\in N\left(v_5\right)\setminus N\left(\{v_2,v_3\}\right)$ for all $x\in (V\setminus D)\setminus V\left(C\right)$. Since $g\left(G\right)=5$, $x\notin N\left(v_2\right)\cap N\left(v_3\right)$. W.l.o.g assume that $x\notin N\left(v_3\right)$. Then there exists $y\in D\setminus \{v_1,v_4\}$ such that $\{x,v_3\}\subseteq N\left(y\right)$. If $x\in N\left(v_2\right)$, then $〈\{x,v_2,v_3,y\}〉\cong C_4$, a contradiction. Thus $x\notin N\left(v_2\right)$. If $x\notin N\left(v_5\right)$, then there exists $y^{\ast }\in D\setminus \{v_1,v_4\}$ such that $\{x,v_3,v_5\}\subseteq N\left(y^{\ast }\right)$. Therefore, $d\left(y^{\ast }\right)\ge 3$, a contradiction. Thus $x\in N\left(v_5\right)\setminus N\left(\{v_2,v_3\}\right)$ for all $x\in (V\setminus D)\setminus V\left(C\right)$.

Finally we proceed to prove our claim that $|(V\setminus D)\setminus V\left(C\right)|=1$. Suppose on the contrary, there exist distinct vertices $x_1,x_2\in (V\setminus D)\setminus V\left(C\right)$. Then $x_1,x_2\in N\left(v_5\right)\setminus N\left(\{v_2,v_3\}\right)$. Obviously, $x_1$ and $x_2$ are not adjacent, for otherwise, $〈\{x_1,x_2,v_5\}〉\cong C_3$. Since $D$ is a psd-set, there exists $d\in D$ such that $\{x_1,x_2\}\subseteq N\left(d\right)$. But in that case $〈\{x_1,d,x_2,v_5\}〉\cong C_4$, a contradiction. Hence our assumption is wrong and $|(V\setminus D)\setminus V\left(C\right)|=1$.

Let $(V\setminus D)\setminus V\left(C\right)=\left\{u\right\}$. Then $u\in N\left(v_5\right)\setminus N\left(\{v_2,v_3\}\right)$ and as $D$ is an ipsd-set, there exist $u_1,u_2\in D$ such that $\{u,v_2\}=N\left(u_1\right)$ and $\{u,v_3\}=N\left(u_2\right)$. Now to prove that $|D\setminus V\left(C\right)|=2$, observe that for each set $S\subseteq V\setminus D$ such that $\left|S\right|=2$, there exists $z\in \{v_1,v_4,u_1,u_2\}$ such that $S\subseteq N\left(z\right)$. Thus to avoid a $4$-cycle in $G$, we must have $D=\{v_1,v_4,u_1,u_2\}$. Hence $G=〈D\cup (V\setminus D)〉\cong S{K}_4$ and the necessity follows.

Conversely, suppose either $G\cong C_5$ or $G\cong S{K}_4$. If $G\cong C_5$, then any maximal independent set of $G$ is an ipsd-set. If $G\cong S{K}_4$, then the set consisting of all vertices of degree $2$ in $G$ is an ipsd-set of $G$. Thus in either case graph $G$ is an ipsd-graph.□

Remark 3.4

It is interesting to note that every $\alpha$-set of $C_5$ is an ipsd-set of $C_5$, while in case of $S{K}_4$, there is unique ipsd-set consisting of all vertices of degree $2$, which also happens to be unique $\alpha$-set of $S{K}_4$.

Next we characterize separable ipsd-graphs of girth $5$. As noted in Corollary 2.2, if $G$ is a separable ipsd-graph of girth $5$, then every block of $G$ must be an ipsd-block. From Theorem 2.4, every block of $G$ must be of girth $5$. Further, as every triangle free ipsd-graph having at least two non-trivial is $C_5$-free (Corollary 2.3), the graph $G$ must have a unique non-trivial block isomorphic to either $C_5$ or $S{K}_4$.

Theorem 3.5

Let $G$ be a separable graph with girth 5. Then $G$ is an ipsd graph if and only if the following conditions hold:

(a)	$G$ has unique non-trivial block $B$ isomorphic to either $C_5$ or $S{K}_4$ and
(b)	every vertex in $V\left(G\right)\setminus V\left(B\right)$ is a pendant vertex having its support in $V\left(B\right)\setminus Q$ where $Q$ is an $\alpha$ -set of $B$ .

Proof

Let $G$ be an ipsd-graph. Since $g\left(G\right)=5$, $G$ is not $C_5$-free, hence from Corollary 2.3, it follows that $G$ has unique non-trivial block (say) $B$. As $G$ is an ipsd-graph, from Corollary 2.2, $B$ is an ipsd-block in $G$. Consequently, from Theorem 3.3, $B$ is isomorphic to either $C_5$ or $S{K}_4$. Since $B\cong C_5$ or $S{K}_4$, there does not exist any vertex $w\in V\left(B\right)$ such that $V\left(B\right)\setminus N\left(w\right)$ is independent. Consequently from Theorem 2.1, $B$ has an ipsd-set $F$ and $V\left(G\right)\setminus V\left(B\right)$ consists of pendant vertices with their supports lying in $V\left(B\right)\setminus F$. Let $P$ be the set of all support vertices in $G$. Since $B\cong C_5$ or $S{K}_4$ and $F$ is an ipsd-set of $B$, it is easy to see that $F$ is an $\alpha$-set of $B$. Consequently, $Q=F\cup (V\left(G\right)\setminus V\left(B\right))$ is an $\alpha$-set of $G$. As $P\subseteq V\left(B\right)\setminus Q$, all the three conditions (a), (b) and (c) follow.

Conversely, assume that (a), (b) and (c) are satisfied. Then it is easy to see that the set $(V\left(G\right)\setminus V\left(B\right))\cup Q$ forms an ipsd-set for graph $G$. Hence the theorem.□

Remark 3.6

Since ${\gamma }_{ips}\left(C_5\right)=\alpha \left(C_5\right)=2$ and ${\gamma }_{ips}\left(S{K}_4\right)=\alpha \left(S{K}_4\right)=4$, from Remark 3.4 and Theorem 3.5, for any ipsd-graph $G$ of girth $5$, $${\gamma }_{ips}\left(G\right)=\alpha \left(G\right)=\left\{\begin{array}{cc}\hfill e+2& \text{if}B\cong C_5,\hfill \\ \hfill e+4& \text{if}B\cong S{K}_4.\hfill \end{array}\right.$$where $B$ is the unique block of $G$ and $e$ is the number of pendant vertices in $G$.

Having characterized ipsd-graphs of girth $5$, we proceed to characterize ipsd-graphs of girth $4$. Again since girth $4$ graphs are triangle free graphs, from Corollary 2.3 and Theorem 2.4, every block of an ipsd-graph of girth $4$ is an ipsd-block of girth $4$. In view of Theorem 2.1, to have complete information about ipsd-graphs of girth $4$, it is enough to characterize $2$-connected ipsd-graphs of girth $4$. Moreover, if $G$ is an ipsd-graph of girth $4$ having at least two non-trivial blocks, then every block of $G$ is $C_5$-free ipsd-block of girth $4$. Thus to achieve our objective, we first consider $2$-connected $C_5$-free ipsd-graphs with $girth\left(G\right)=4$.

Theorem 3.7

Let $G$ be a $2$ -connected $C_5$ -free graph with $girth\left(G\right)=4$ . Then $G$ is an ipsd-graph if and only if one of the following holds:

1.

There exists $w\in V\left(G\right)$ such that $V\left(G\right)\setminus N\left(w\right)$ is independent.

2.

There exist non-adjacent vertices $u,v$ such that $N\left(u\right)$ , $N\left(v\right)$ are disjoint independent subsets of $V\left(G\right)$ and $〈N\left(u\right)\cup N\left(v\right)〉\cong K_{m,n}$ , where $m=\left|N\left(u\right)\right|$ and $n=\left|N\left(v\right)\right|$ . Moreover, for any vertex $w\in V\left(G\right)\setminus (N\left[u\right]\cup N\left[v\right])$ either $N\left(w\right)\subset N\left(u\right)$ or $N\left(w\right)\subset N\left(v\right)$ .

Proof

For the sufficient part, observe that if (1) is satisfied, then from Proposition 1.7, $G$ is an ipsd-graph. If (2) holds, then $D=V\left(G\right)\setminus (N\left(u\right)\cup N\left(v\right))$ is an ipsd-set of graph $G$.

Now to prove necessary part, let $G$ be an ipsd-graph and $D$ be an ipsd set of $G$. If $G$ satisfies condition (1), then we are through. Therefore let condition (1) is not satisfied.

Claim 1. There exists a cycle $C\cong C_4$ of length $4$ such that two non-adjacent vertices of $C$ are in $D$.

Since $girth\left(G\right)=4$, there exists a cycle $C^1$ of length $4$ in $G$. If two non adjacent vertices of $C^1$ are in $D$, then $C^1$ is the required cycle and we are done with our claim. Thus let $C^1=(u_1,u_2,u_3,u_4,u_1)$ be such that $u_1,u_2,u_3\in V\setminus D$. Since (1) is not satisfied, there exist adjacent vertices $x_1,x_2\in V\left(G\right)\setminus N\left(u_2\right)$. Since $D$ is independent, both $x_1$ and $x_2$ cannot be in $D$. If both $x_1$ and $x_2$ are in $V\setminus D$, then as $x_1,x_2\notin N\left(u_2\right)$ and $D$ is ipsd-set, there exists $d_i\in D$ such that $x_i,u_2\in N\left(d_i\right)$ for each $i=1,2$. If $d_1=d_2$, then $〈x_1,x_2,d_1〉\cong C_3$, a contradiction to the fact that $girth\left(G\right)=4$. But then $〈u_2,d_1,x_1,x_2,d_2〉\cong C_5$, again a contradiction as $G$ is $C_5$-free. Thus exactly one of $x_1$ and $x_2$ is in $D$.

Without loss of generality, assume that $x_1\in D$ and $x_2\in V\setminus D$. Since $x_2,u_2\in V\setminus D$, there exists $d$ in $D$ such that $x_2,u_2\in N\left(d\right)$. Since $G$ is $2$-connected, there exists $x_3\in N\left(x_1\right)\cap (V\setminus D)$. Clearly, $x_3$ and $x_2$ are non-adjacent. For otherwise, $〈x_1,x_2,x_3〉\cong C_3$, a contradiction. If $x_3\in N\left(u_2\right)$, then $〈u_2,x_3,x_1,x_2,d,u_2〉\cong C_5$, contradiction. Thus $x_3\notin N\left(u_2\right)$. Now $\{x_3,x_2,u_2\}$ is an independent subset of $V\setminus D$, therefore there exists $d^{\ast }\in D$ such that $\{x_3,x_2,u_2\}\subseteq N\left(d^{\ast }\right)$. If $d=d^{\ast }$, then $C^2=〈x_1,x_2,d,x_3〉\cong C_4$ such that two non adjacent vertices $d$ and $x_1$ of the cycle are in $D$. If $d\ne d^{\ast }$, then $C^3=〈x_2,d,u_2,d^{\ast }〉\cong C_4$ and $d,d^{\ast }\in D$. Hence the claim.

Let $C=(v_1,v_2,v_3,v_4,v_1)$ be the cycle of length $4$ and $v_1,v_3\in V\left(C\right)\cap D$. Let $X=(V\setminus D)\cap N\left(v_2\right)\cap N\left(v_4\right)$ and $Y=(V\setminus D)\setminus [N\left(v_2\right)\cup N\left(v_4\right)]$.

Claim 2. $V\setminus D=X\cup Y$ and $X$, $Y$ are independent sets.

Suppose there exists $x\in V\setminus D$ such that $x\in N\left(v_2\right)\setminus N\left(v_4\right)$. Since $girth\left(G\right)=4$ and $x,v_1,v_3\in N\left(v_2\right)$, therefore $x\notin N\left(v_1\right)\cup N\left(v_3\right)$. Since $\{x,v_4\}$ is an independent set in $V\setminus D$, there exists $d\in D\setminus \{v_1,v_3\}$ such that $\{x,v_4\}\subset N\left(d\right)$. But then $〈v_1,v_2,x,d,v_4〉\cong C_5$, contradiction. Hence $V\setminus D=X\cup Y$.

If $x_1,x_2\in X$ be two adjacent vertices, then $〈x_1,x_2,v_2〉\cong C_3$, contradiction. Hence $X$ is independent set. If $Y$ is not independent, there exist two adjacent vertices $y_1,y_2\in Y$. Since $y_1,y_2\notin N\left(v_2\right)$, there exists $d_1,d_2\in D$ such that $\{y_i,v_2\}\subseteq N\left(d_i\right)$ for each $i$. But then $〈v_2,d_1,y_1,y_2,d_2,v_2〉\cong C_5$, a contradiction. Hence $Y$ is independent.

Claim 3. $〈X\cup Y〉\cong K_{\left|X\right|,\left|Y\right|}$ and $X=N\left(u\right)$, $Y=N\left(v\right)$ for some $u,v\in D$.

Since $D$ is ipsd-set and $X$, $Y$ are independent sets in $V\setminus D$, there exists $u,v\in D$ such that $X\subseteq N\left(u\right)$ and $Y\subseteq N\left(v\right)$. Suppose there exists $x\in X$ and $y\in Y$ such that $x$ and $y$ are not adjacent. As $D$ is ipsd-set, there exists a vertex $d_3\in D$ such that $x,y\in N\left(d_3\right)$. But then $〈v_2,v,y,d_3,x〉\cong C_5$, a contradiction. Thus $〈X\cup Y〉=K_{\left|X\right|,\left|Y\right|}$. Since $u\in D$, $N\left(u\right)\subseteq V\setminus D$. If $y^{\ast }\in Y\cap N\left(u\right)$, then $〈x^{\ast },u,y^{\ast }〉\cong C_3$ for any $x^{\ast }\in X$, contradiction. Thus $X=N\left(u\right)$. Similarly, $Y=N\left(v\right)$.

Claim 4. For any $w\in V\left(G\right)\setminus (N\left[u\right]\cup N\left[v\right])$ either $N\left(w\right)\subset N\left(u\right)$ or $N\left(w\right)\subset N\left(v\right)$.

Since $V\setminus D=X\cup Y$, therefore $V\left(G\right)\setminus (N\left[u\right]\cup N\left[v\right])⊊D$. Let $w\in V\left(G\right)\setminus (N\left[u\right]\cup N\left[v\right])$ be any vertex. Then $w\in D$. Consequently, $N\left(w\right)\subseteq V\setminus D=N\left(u\right)\cup N\left(v\right)$. If $x\in N\left(u\right)\cap N\left(w\right)$ and $y\in N\left(v\right)\cap N\left(w\right)$, then $〈x,w,y〉\cong C_3$, contradiction. Thus either $N\left(w\right)\subset N\left(u\right)$ or $N\left(w\right)\subset N\left(v\right)$. Hence the condition (2) holds. Therefore necessity part follows. □

From Theorems 2.1 and 3.7, following theorem on separable $C_5$-free ipsd-graphs of girth $4$ can be easily obtained.

Theorem 3.8

Let $G$ be a $C_5$ -free separable graph with girth $4$ . Then $G$ is an ipsd-graph if and only if exactly one of the following holds:

(i)

$\left|{\mathcal{B}}_G\right|=1$ and one of the following holds (a) there exists $w\in V\left(G\right)$ such that $V\left(G\right)\setminus N\left(w\right)$ is independent (b) there exist non-adjacent vertices $u,v$ such that $N\left(u\right)$ , $N\left(v\right)$ are disjoint independent subsets of $V\left(G\right)$ and $〈N\left(u\right)\cup N\left(v\right)〉\cong K_{m,n}$ , where $m=\left|N\left(u\right)\right|$ and $n=\left|N\left(v\right)\right|$ . Moreover, for any vertex $w\in V\left(G\right)\setminus (N\left[u\right]\cup N\left[v\right])$ either $N\left(w\right)\subset N\left(u\right)$ or $N\left(w\right)\subset N\left(v\right)$ .

(ii)

$\left|{\mathcal{B}}_G\right|\ge 2$ and there exists a cut vertex $w$ in $G$ such that $V\left(G\right)\setminus N\left(w\right)$ is independent

Having characterized $C_5$-free ipsd-graphs $G$ with $girth\left(G\right)=4$, what can we say about ipsd-graphs of girth $4$ containing an induced subgraph isomorphic to $C_5$? In what follows we make a partial answer to this question by focusing on circumference of ipsd-graphs.

Note that circumference of an ipsd-graph of girth $5$ is either $5$ or $8$. But in case of ipsd-graphs of girth $4$, for any positive integer $k$, there always exists an ipsd-graph of girth $4$ having circumference greater than $k$. In fact, for an instance, for any integer $n$, the graph $S\left(W_n\right)$ (see Fig. 4) obtained from wheel $W_n$ by subdividing each edge of the cycle $C_n$ of $W_n$ is an ipsd-graph of girth $4$ and circumference $2n$.

Fig. 4 Graph $S\left(W_6\right)$ obtained from wheel $W_6$ by subdividing each edge of the cycle.

If we consider 2-connected ipsd-graphs with girth $4$ and circumference $5$, then we have its complete structural information. Thus giving partial information about graphs with girth $4$ containing an induced 5-cycle. But before characterizing such graphs, we introduce an equivalence relation on graphs using the notion of duplicate vertices [8].

Definition 3.9

[8] Two vertices $u$ and $v$ (need not be distinct) in a graph $G$ are said to be duplicated if $N\left(u\right)=N\left(v\right)$.

If vertices $u$ and $v$ are duplicated in $G$, then we say that $u$ and $v$ are duplicates of each other. By definition, every vertex is a duplicate vertex of itself. It is evident that the concept of duplicate vertices in a graph $G$ partitions the vertex set $V\left(G\right)$ into disjoint equivalence classes. For a vertex $u$ in graph $G$, let $$\left[u\right]=\{v\in V\left(G\right):v\text{is a duplicate of}u\}$$denote the equivalence class containing the vertex $u$. It is interesting to note that each equivalence class is an independent set. Also, for any graph $G$, $d\left(x\right)=d\left(u\right)$ for all $x\in \left[u\right]$.

Notation 3.10

For any graph $G$ and any vertex $u\in V\left(G\right)$ , let ${\left[u\right]}^{\ast }=\left[u\right]\setminus \left\{u\right\}$ .

Observation 3.11

If $u$ and $v$ are adjacent vertices of degree $2$ in a graph $G$ , then ${\left[u\right]}^{\ast }\ne 0̸$ and ${\left[v\right]}^{\ast }\ne 0̸$ if and only if $G\cong C_4$ .

Proof

Suppose ${\left[u\right]}^{\ast }\ne 0̸$ and ${\left[v\right]}^{\ast }\ne 0̸$ and let $u^{\ast }\in {\left[u\right]}^{\ast }$ and $v^{\ast }\in {\left[v\right]}^{\ast }$. Then $N\left(u\right)=\{v,v^{\ast }\}$, $N\left(v\right)=\{u,u^{\ast }\}$ and $〈u,v,u^{\ast },v^{\ast }〉\cong C_4$. Since degree of each vertex $u,u^{\ast },v,v^{\ast }$ is $2$, therefore $G\cong C_4$. Hence the necessity. Sufficient part is trivial. □

Definition 3.12

Vertex Identification [18] To identify non-adjacent vertices $u$ and $v$ of a graph $G$ is to replace these vertices by a single vertex adjacent to all the vertices which were adjacent in G to either $u$ or $v$.

Definition 3.13

$H$-Duplicate We will call a graph $G$ to be duplicate of graph $H$ or $H$-duplicate if $H$ can be obtained from $G$ by identifying all vertices in each degree-$2$ equivalence class of duplicate vertices.

Note that if a graph $G$ is duplicate of graph $H$, then $H$ can be treated as a subgraph of $G$. In that case, $d_G\left(u\right)=2$ for all $u\in V\left(G\right)\setminus V\left(H\right)$ and $$V\left(G\right)=\bigcup _{u\in V\left(H\right)}{\left[u\right]}_G,$$where ${\left[u\right]}_G$ is the set of all duplicate vertices of $u$ in $G$.

Definition 3.14

Duplicated Equivalent Two graphs $G_1$ and $G_2$ will be called duplicated equivalent if there exists a graph $G$ such that both $G_1$ and $G_2$ are $G$-duplicate. If $G_1$ is duplicated equivalent to $G_2$, then we will denote it as $G\asymp G_2$. It is easy to see that the relation $\asymp$ is an equivalence relation on graphs.

Lemma 3.15

A $2$ -connected graph $G$ is $C_5$ duplicated if and only if either $G\cong C_5$ or there exists an induced subgraph $C$ of $G$ isomorphic to $C_5$ and an $\alpha$ -set $\{u,v\}$ of $C$ such that $V\left(G\right)\setminus V\left(C\right)={\left[u\right]}^{\ast }\cup {\left[v\right]}^{\ast }$ .

Proof

Let $G$ be $C_5$ duplicated. If $G\cong C_5$, then we have nothing to prove. Let $G\ncong C_5$, then as $G\asymp C_5$, there exists an induced subgraph $C=(u_1,u_2,u_3,u_4,u_5,u_1)$ of $G$ isomorphic to $C_5$ such that $$V\left(G\right)\setminus V\left(C\right)={\cup }_{i=1}^5{\left[u_i\right]}^{\ast }\text{and}d\left(x\right)=2\forall x\in V\left(G\right)\setminus V\left(C\right).$$

Let $y\in V\left(G\right)\setminus V\left(C\right)$. Then $y\in {\left[u_i\right]}^{\ast }$ for some $i=1,2,\dots ,5$. W.l.o.g assume that $y\in {\left[u_1\right]}^{\ast }$. Since $u_1\in N\left(u_2\right)\cap N\left(u_5\right)$, $y\in N\left(u_2\right)\cap N\left(u_5\right)$. Consequently, ${\left[u_2\right]}^{\ast }={\left[u_5\right]}^{\ast }=0̸$. Thus $$V\left(G\right)\setminus V\left(C\right)={\left[u_1\right]}^{\ast }\cup {\left[u_3\right]}^{\ast }\cup {\left[u_4\right]}^{\ast }.$$

If both ${\left[u_3\right]}^{\ast }$ and ${\left[u_4\right]}^{\ast }$ are non-empty set, then $d\left(u_3\right)=d\left(u_4\right)=2$, which contradicts Observation 3.11. Hence at least one of ${\left[u_3\right]}^{\ast }$ and ${\left[u_4\right]}^{\ast }$ is an empty set. W.l.o.g assume that ${\left[u_3\right]}^{\ast }=0̸$. Then $V\left(G\right)\setminus V\left(C\right)={\left[u_1\right]}^{\ast }\cup {\left[u_4\right]}^{\ast }$. Hence the necessity. Sufficiency is trivial.□

Theorem 3.16

Let $G$ be a 2-connected graph with girth $g\left(G\right)=4$ and circumference $c\left(G\right)=5$ , then $G$ is an ipsd-graph if and only if $G\asymp C_5$ and $G\ncong C_5$ .

Proof

Let $G$ be an ipsd-graph girth $4$ and circumference $5$. Trivially, $G\ncong C_5$. In view of Lemma 3.15, to prove necessity, we need to show the existence of an induced subgraph $C$ of $G$ isomorphic to $C_5$ and an $\alpha$-set $\{u,v\}$ of $C$ such that $V\left(G\right)\setminus V\left(C\right)={\left[u\right]}^{\ast }\cup {\left[v\right]}^{\ast }$.

Since circumference $c\left(G\right)=5$ and girth $g\left(G\right)=4$, $G$ has an induced subgraph isomorphic to $C_5$. Let $C=(u_1,u_2,u_3,u_4,u_5,u_1)$ be any induced $5$-cycle in $G$. Let $D$ be an ipsd-set of $G$. Since $D$ is independent, $|V\left(C\right)\cap D|\le 2$.

Claim: $|V\left(C\right)\cap D|=2$.

Suppose, on the contrary, $|V\left(C\right)\cap D|\le 1$. W.l.o.g assume that $\{u_2,u_3,u_4,u_5\}\subseteq V\setminus D$. Then $\{u_2,u_4\}$ and $\{u_3,u_5\}$ are independent sets in $V\setminus D$. Since $D$ is an ipsd-set and $g\left(G\right)=4$, there exist two distinct vertices $x,y\in D$ such that $\{u_2,u_4\}\subseteq N\left(x\right)$ and $\{u_3,u_5\}\subseteq N\left(y\right)$. But then $(u_2,x,u_4,u_5,y,u_3,u_2)$ is a 6-cycle in $G$, contradiction to the fact that $c\left(G\right)=5$. Thus $|V\left(C\right)\cap D|=2$.

W.l.o.g we assume that $V\left(C\right)\cap D=\{u_1,u_3\}$. Two cases arise:

Case 1. $\left|D\right|=2$ i.e., $D=\{u_1,u_3\}$

Claim 1: $V\left(G\right)\setminus V\left(C\right)\subseteq N\left(u_1\right)$ or $V\left(G\right)\setminus V\left(C\right)\subseteq N\left(u_3\right)$.

On the contrary, let $x\in [V\left(G\right)\setminus V\left(C\right)]\setminus N\left(u_1\right)$ and $y\in [V\left(G\right)\setminus V\left(C\right)]\setminus N\left(u_3\right)$. As $x\in N\left(u_3\right)\setminus N\left(u_1\right)$, $y\in N\left(u_1\right)\setminus N\left(u_2\right)$ and $D$ is an ipsd-set, $x$ and $y$ must be adjacent vertices. But then $(u_1,u_5,u_4,u_3,x,y)$ forms a 6-cycle, contradiction. Hence either $V\left(G\right)\setminus V\left(C\right)\subseteq N\left(u_1\right)$ or $V\left(G\right)\setminus V\left(C\right)\subseteq N\left(u_3\right)$.

W.l.o.g assume that $V\left(G\right)\setminus V\left(C\right)\subseteq N\left(u_1\right)$.

Claim 2: $V\left(G\right)\setminus V\left(C\right)\subseteq N\left(u_3\right)\cup N\left(u_4\right)$.

Let, if possible, there exists $x\in [V\left(G\right)\setminus V\left(C\right)]\setminus (N\left(u_3\right)\cup N\left(u_4\right))$. But then as $\{x,u_4\}$ is an independent subset of $V\setminus D$, $\{u_4,x\}⊈N\left(u_1\right)$ and $\{u_4,x\}⊈N\left(u_3\right)$, we arrive at a contradiction due to the fact that $D$ is an ipsd-set. Hence $V\left(G\right)\setminus V\left(C\right)\subseteq N\left(u_3\right)\cup N\left(u_4\right)$.

Thus $V\left(G\right)\setminus V\left(C\right)=N\left(u_1\right)\cap (N\left(u_3\right)\cup N\left(u_4\right))$. As $G$ is $C_3$-free, $V\left(G\right)\setminus \{u_1,u_3,u_4\}$ is an independent set and every vertex in $V\left(G\right)\setminus \{u_1,u_3,u_4\}$ has degree $2$. Hence $V\left(G\right)\setminus V\left(C\right)={\left[u_2\right]}^{\ast }\cup {\left[u_5\right]}^{\ast }$. Thus, from Lemma 3.15, $G$ is $C_5$-duplicated.

Case 2. $\left|D\right|\ge 2$ i.e., $\{u_1,u_3\}⊊D$.

Claim 1: $D\subseteq N\left(\{u_2,u_4,u_5\}\right)$.

Suppose, on the contrary, there exists $x\in D\setminus N\left(\{u_2,u_4,u_5\}\right)$. As $d\left(x\right)\ge 2$ and $G$ is $C_3$-free, there exist non-adjacent vertices $y,z\in N\left(x\right)$. Again, as $G$ is $C_3$-free, $y\notin N\left(u_4\right)\cap N\left(u_5\right)$. W.l.o.g we can assume that $y\notin N\left(u_4\right)$. Since $\{y,u_4\}$ is an independent set in $V\setminus D$, there exists $d\in D$ such that $\{y,u_4\}\subseteq N\left(d\right)$. If $z\in N\left(u_5\right)$, then $(z,u_5,u_4,d,y,x,z)$ is a 6-cycle in $G$, contradiction. If $z\notin N\left(u_5\right)$, there exists $d^{\ast }\in D$ such that $\{z,u_5\}\subseteq N\left(d^{\ast }\right)$. Since $G$ is $C_3$-free, $d^{\ast }\ne d$. Consequently, $(z,x,y,d,u_4,u_5,d^{\ast },z)$ is a 7-cycle in $G$, a contradiction. Hence $D\subseteq N\left(\{u_2,u_4,u_5\}\right)$.

Claim 2: $D\subseteq N\left(u_2\right)$.

Let, if possible, there exists $x\in D\setminus N\left(u_2\right)$. As $G$ is $C_3$-free and $D\subseteq N\left(\{u_2,u_4,u_5\}\right)$, $x\in N\left(u_4\right)△N\left(u_5\right)$. W.l.o.g assume that $x\in N\left(u_4\right)\setminus N\left(u_5\right)$. Since $d\left(x\right)\ge 2$, there exists $y(\ne u_4)\in N\left(x\right)$. If $y\in N\left(u_2\right)$, then $(y,x,u_4,u_5,u_1,u_2,y)$ is a 6-cycle, a contradiction. Hence $y\notin N\left(u_2\right)$. Then $\{u_4,y,u_2\}$ is an independent set in $V\setminus D$ and therefore there exists $d\in D$ such that $\{u_4,y,u_2\}\subseteq N\left(d\right)$. But then $(y,x,u_4,u_5,u_1,u_2,d,y)$ is a 7-cycle, yielding a contradiction. Hence our assumption is wrong and $D\subseteq N\left(u_2\right)$.

Claim 3: $N\left(u\right)⊊\{u_2,u_4,u_5\}$ for all $u\in D\setminus \{u_1,u_3\}$.

On the contrary, let $w\in D\setminus \{u_1,u_3\}$ such that $N\left(u\right)⊈\{u_2,u_4,u_5\}$. Let $y\in N\left(w\right)\setminus \{u_2,u_4,u_5\}$. As $w\in N\left(u_2\right)\cap [N\left(u_4\right)△N\left(u_5\right)]$, w.l.o.g assume that $w\in N\left(u_2\right)\cap N\left(u_4\right)$ and $w\notin N\left(u_5\right)$. If $y\in N\left(u_5\right)$, then $(y,u_5,u_1,u_2,u_3,u_4,w,y)$ is a 7-cycle in $G$, a contradiction. If $y\notin N\left(u_5\right)$, then there exists $d\in D$ such that $u_5,y\in N\left(d\right)$. But then $(y,d,u_5,u_4,u_3,u_2,w,y)$ is a 7-cycle in $G$, again a contradiction. Hence $N\left(u\right)\subseteq \{u_2,u_4,u_5\}$ and $d\left(u\right)=2$ (as $G$ is $C_5$-free) for all $u\in D\setminus \{u_1,u_3\}$.

Subcase I. $V\setminus D=\{u_2,u_4,u_5\}$

In this case ${\left[u_1\right]}^{\ast }=N\left(u_5\right)\setminus \{u_1,u_4\}$, ${\left[u_3\right]}^{\ast }=N\left(u_4\right)\setminus \{u_3,u_5\}$ and $d\left(x\right)=2$ for every $x\in D$. It follows from Lemma 3.15 that $G$ is $C_5$-duplicated.

Subcase II. $\{u_2,u_4,u_5\}⊊V\setminus D$

Since $\{u_1,u_3\}⊊D$, there exists $w\in D\setminus \{u_1,u_3\}$. Then $d\left(w\right)=2$ and either $N\left(w\right)=\{u_2,u_4\}$ or $N\left(w\right)=\{u_2,u_5\}$. W.l.o.g we assume that $N\left(w\right)=\{u_2,u_4\}$. Then $C^{\ast }=(u_1,u_2,w,u_4,u_5)$ is a 5-cycle in $G$ having two vertices in $D$. By interchanging the roles of $u_3$ and $w$, from Case 1, it follows that $N\left(u_3\right)=\{u_2,u_4\}$ and $d\left(u_3\right)=2$.

Claim: $(V\setminus D)\setminus \{u_2,u_4\}=N\left(u_1\right)\cap N\left(u_4\right)$.

Since $N\left(x\right)\subseteq \{u_2,u_4,u_5\}$ for every $x\in D\setminus \left\{u_1\right\}$ and $D$ is a dominating set, therefore $(V\setminus D)\setminus \left\{u_4\right\}=N\left(u_1\right)$. Further, since $G$ is $2$-connected $C_5$-free graph, $(V\setminus D)\setminus \{u_2,u_4\}\subseteq N\left(u_4\right)$. It follows that $(V\setminus D)\setminus \{u_2,u_4\}=N\left(u_1\right)\cap N\left(u_4\right)$ and every vertex in $(V\setminus D)\setminus \{u_2,u_4\}$ has degree $2$.

Next we claim that $D\setminus \left\{u_1\right\}=N\left(u_2\right)\cap N\left(u_4\right)$. Suppose, on the contrary, there exists $w^{\prime }\in D\setminus \left\{u_1\right\}$ such that $w^{\prime }\notin N\left(u_2\right)\cap N\left(u_4\right)$. Then $w^{\prime }\in N\left(u_2\right)\cap N\left(u_5\right)$ and for any $y\in (V\setminus D)\setminus \{u_2,u_4,u_5\}$, the cycle $(u_5,w^{\prime },u_2,u_3,u_4,y,u_1)$ is a 7-cycle in $G$, contradiction. Thus $D\setminus \left\{u_1\right\}=N\left(u_2\right)\cap N\left(u_4\right)$.

Observe that ${\left[u_5\right]}^{\ast }=(V\left(G\right)\setminus D)\setminus \{u_2,u_4,u_5\}$ and ${\left[u_3\right]}^{\ast }=D\setminus \{u_1,u_3\}$. Thus $V\left(G\right)\setminus V\left(C\right)={\left[u_3\right]}^{\ast }\cup {\left[u_5\right]}^{\ast }$ and hence $G$ is $C_5$-duplicated.

Conversely, suppose $G\asymp C_5$ and $G\ncong C_5$, then by Lemma 3.15, there exists an induced 5-cycle $C$ in $G$ such that $V\left(G\right)\setminus V\left(C\right)={\left[u\right]}^{\ast }\cup {\left[v\right]}^{\ast }$, where $\{u,v\}$ is a maximal independent set in $C$. Then it is evident that $D=\{u,v\}$ is an ipsd-set of $G$. Hence $G$ is an ipsd-graph.□

Remark 3.17

If $G$ is duplicated equivalent to $C_5$ and $C=(u_1,u_2,u_3,u_4,u_5,u_1)$ is an induced $5$-cycle in $G$ such that $V\left(G\right)\setminus V\left(C\right)={\left[u_1\right]}^{\ast }\cup {\left[u_3\right]}^{\ast }$, then $$\alpha \left(G\right)=\Delta \left(G\right)=d\left(u_2\right)\text{and}{\gamma }_{ips}\left(G\right)=2.$$

In fact, the collection $\mathfrak{I}=\left\{\{u_2,u_5\},\{u_2,u_4\},\left[u_1\right]\cup \left\{u_4\right\},\left[u_3\right]\cup \left\{u_5\right\},\left[u_1\right]\cup \left[u_3\right]\right\}$ is the set of all maximal independent sets in $G$. Moreover, $\mathfrak{I}$ is also the set of all ipsd-sets of $G$.

The following theorem characterizes separable ipsd-graphs with girth $g\left(G\right)=4$ and circumference $c\left(G\right)=5$.

Theorem 3.18

Let $G$ be a separable graph with girth $g\left(G\right)=4$ and circumference $c\left(G\right)=5$ , then $G$ is an ipsd-graph if and only if the following conditions hold:

(a)	$G$ has unique non-trivial block $B(\ncong C_5)$ duplicated equivalent to $C_5$ and
(b)	every vertex in $V\left(G\right)\setminus V\left(B\right)$ is a pendant vertex having its support in $V\left(B\right)\setminus Q$ where $Q$ is an $\alpha$ -set of $B$ .

Proof

Suppose $G$ is an ipsd-graph. Since $g\left(G\right)=4$ and $c\left(G\right)=5$, $G$ is triangle free but not $C_5$-free. From Corollary 2.3, $G$ has a unique non-trivial block (say) $B$. Then from Corollary 2.2, $B$ is an ipsd-block of $G$. Obviously, girth of $B$ is $4$ and circumference of $B$ is $5$. Consequently, from Theorem 3.16, $B\ncong C_5$ and $B\asymp C_5$. Then there does not exist any $w\in G$ such that $V\left(G\right)\setminus N\left(w\right)$ is an independent set. Hence from Theorem 2.1, $B$ has an ipsd-set $Q$ and $V\left(G\right)\setminus V\left(B\right)$ consists of pendant vertices with their supports lying in $V\left(B\right)\setminus Q$. As noted in Remark 3.17, every ipsd-set of $B$ is an $\alpha$-set of $B$. Hence the necessity follows.

For the sufficiency, observe that the set $(V\left(G\right)\setminus V\left(B\right))\cup Q$ forms an ipsd-set of $G$. Hence $G$ is an ipsd-graph.□

4 Concluding remarks

In this paper, we first proved that girth of an ipsd-graph is always less than equal to $5$ and thereafter, characterized ipsd-graphs with girth $5$. We could characterize $C_5$-free ipsd-graphs of girth $4$. Also, using the graph equivalence relation, duplicated equivalence, we exhibited a class of ipsd-graphs of girth $4$ having $C_5$ as an induced subgraph. But the general problem of characterizing ipsd-graphs of girth $4$ having $C_5$ as an induced subgraph is still open.

Problem 1

Characterize ipsd-graphs of girth $4$ containing $C_5$ as an induced subgraph.

Also, we are yet to explore ipsd-graphs of girth $3$ and it would be interesting to characterize them. As we have seen in case of separable ipsd-graphs of girth $4$, that characterizing separable graphs boils down to the problem of characterizing $2$-connected ipsd-graphs. Thus to tackle the problem of characterizing ipsd-graphs of girth $3$, one must first consider $2$-connected ipsd-graphs of girth $3$.

Problem 2

Characterize $2$-connected ipsd-graphs of girth $3$.

In this paper, we introduced a graph equivalence relation, called duplicated equivalent. In Lemma 3.15, we presented equivalence class of $C_5$ w.r.t duplicated relation. It would be interesting to find equivalence classes of various other well known graphs. In [19], graph equations (w.r.t graph equivalence relation for isomorphism) for line graphs, total graphs, middle graphs and quasi-total graphs were solved. Similar graph equations w.r.t duplicated equivalence relation can be considered.

Problem 3

Under what condition a graph pair $(G,H)$ is a solution to the following equation: $$[1.]L\left(G\right)\asymp M\left(H\right)[2.]L\left(G\right)\asymp T\left(H\right)[3.]L\left(G\right)\asymp P\left(H\right)[4.]L\left(G\right)\asymp M\left(H\right)[5.]L\left(G\right)\asymp T\left(H\right)[6.]L\left(G\right)\asymp P\left(H\right)$$ where $L\left(G\right),M\left(G\right),T\left(G\right)$ and $P\left(G\right)$ represent line graph, middle graph, total graph and quasi-total graph, respectively, of graph $G$.