Compressive deformation of liquid phase-sintered porous silicon carbide ceramics

Peer review under responsibility of The Ceramic Society of Japan and the Korean Ceramic Society.

Abstract

Porous silicon carbide ceramics were fabricated by liquid phase sintering with 1 wt% Al₂O₃–1 wt% Y₂O₃ additives during hot-pressing at 1400–1900 °C. The longitudinal strain at compressive fracture increased at a higher porosity and was larger than the lateral strain. The compressive Young's modulus and the strain at fracture depended on the measured direction, and increased with the decreased specific surface area due to the formation of grain boundary. However, the compressive strength and the fracture energy were not sensitive to the measured direction. The compressive strength of a porous SiC compact increased with increasing grain boundary area. According to the theoretical modeling of the strength–grain boundary area relation, it is interpreted that the grain boundary of a porous SiC compact is fractured by shear deformation rather than by compressive deformation.

Keywords:

• Compressive strength
• Porosity
• Liquid phase sintering
• Silicon carbide

1 Introduction

Porous ceramics have been widely used as a filter, a separation membrane, a catalyst support or an electrode of electrochemical cell because of its high thermal, mechanical and chemical stability. In our previous papers, gas permeability of porous alumina and SiC ceramics [1,2] was measured for H₂, CO₂, N₂ and Ar gases to understand the influence of pore structure on the flux of gas transported. We have also developed useful porous electrochemical cells, which promote the formation of hydrogen by reforming of biogas (CH₄ + CO₂ → 2H₂ + 2CO) [3–5] or by water-gas shift reaction (CO + H₂O → H₂ + CO₂) [6], and the decomposition of CO and CO₂ gases to solid carbon and O₂ gas (CO → C + ½O₂) [7].

In addition to the chemical interaction between the pores of a material and supplied gas molecules, the mechanical properties of a porous ceramics have been studied. Eq. (1)(1) $\sigma ={\sigma }_0\exp (-bP)$(1) shows an empirical relation of the fracture strength (σ) and porosity (P) [8],(1) $\sigma ={\sigma }_0\exp (-bP)$(1) where σ₀ and b are the strength at P = 0% and the experimental parameter, respectively. The empirical relation has been often observed in porous alumina, silicon carbide [9] and hydroxyapatite ceramics [10]. Recently, we clarified that the compressive strength of porous alumina ceramics is related to the neck area between adjacent two grains and the number of grains packed in the calcined powder compact. In this paper, the deformation behavior, Young's modulus and compressive strength were measured in parallel and perpendicular directions to the hot-pressing direction of liquid phase-sintered SiC. A porous SiC ceramics is an important material as a diesel particulate filter. Significant anisotropic mechanical properties were observed in the hot-pressed porous SiC compacts.

2 Experimental

SiC powder produced by Yakushima Electric Industry (Kagoshima, Japan) was used with following properties: chemical composition, 0.66 mass% SiO₂, 0.37 mass% free C, 0.004 mass% Al, 0.013 mass% Fe, median size 800 nm, specific surface area 15.85 m²/g, isoelectric point pH 2.5. As sintering additives, Al₂O₃ powder (purity Al₂O₃ > 99.99 mass%, median size 310 nm, specific surface area 10.8 m²/g, isoelectric point pH 8.0, Sumitomo Chemical Industry Co., Ltd., Tokyo, Japan) and Y₂O₃ powder (purity Y₂O₃ > 99.9 mass%, median size 290 nm, specific surface area 15.0 m²/g, isoelectric point pH 7.5, Shin-Etsu Chemical Industry Co., Ltd., Tokyo, Japan) were employed. These powders were mixed at a weight ratio of SiC:Al₂O₃:Y₂O₃ = 1:0.01:0.01 and dispersed in double-distilled water at a solid content of 30 vol% at pH 5.0. The suspension was stirred for 24 h and then consolidated on a gypsum board. The consolidated powder compact was placed in a carbon mold and hot-pressed at 1400–1900 °C for 2 h under a pressure of 39 MPa in an argon atmosphere (FVPHP-5-R, Fuji Dempa Kogyo Co., Ltd., Osaka, Japan). The sintered SiC sample was cut into a rectangular prism of 5 × 5 × 6 mm. The bulk density of sintered sample was measured by the Archimedes method using a kerosene medium. The specific surface area was measured using the Brunauer–Emmett–Teller (BET) method (Flow Sorb II 2300, Shimadzu Co., Japan). The microstructure of SiC was observed using a field emission scanning electron microscope (FE-SEM, S-4100H, Hitachi High-Technologies Co., Japan) after the chemical etching by heating the sintered SiC sample in an aqueous solution of 85 mol% NaCl–15 mol% NaOH at 800 °C for 20 min.

In a compression test, the SiC sample was sandwiched between two laminates composed of copper-plate (20 × 20 × 1 mm), sintered-SiC-plate (20 × 18 × 7 mm) and copper-plate (20 × 20 × 1 mm), and then compressed at a crosshead speed of 0.1 mm/min under a load <6 kN [11]. The mechanical properties of SiC sample were measured in two directions parallel and perpendicular to the hot-pressing direction. During the compression test, the longitudinal and lateral strains of sample were measured to evaluate the Poisson's ratio (Sensor Interface, PCD-300B-F, Kyowa Electronic Instruments Co., Ltd., Japan). The compression test was carried out four times for each hot-pressing condition to examine the reproducibility of the measurement.

3 Results and discussion

3.1 Densification of SiC compact

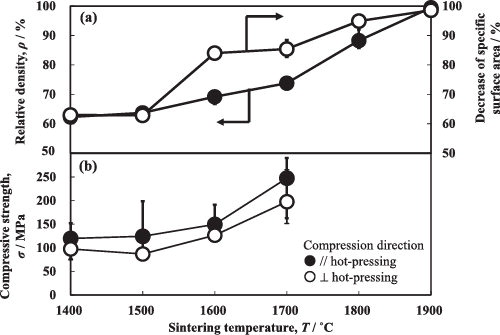
Fig. 1(a) shows the relative density and the decrease in the specific surface area during the hot-pressing at 1400–1900 °C. The decrease in the specific surface area is based on the value of 15.85 m²/g of the starting SiC powder. The densification of SiC by the liquid phase sintering with SiO₂–Al₂O₃–Y₂O₃ liquid [12] was accompanied by the decrease of the specific surface area. This tendency was different from the solid state sintering of an alumina compact [11]. The relative density of the alumina compact was almost constant (60–63% relative density) at 500–1000 °C but the specific surface area decreased with increasing sintering temperature. The decreased specific surface area of alumina compact at low temperatures is related to the increase of grain boundary area. In the SiC compact, the grain boundary development and densification occurred simultaneously. Fig. 2 shows the microstructures of SiC hot-pressed at 1400–1900 °C for 2 h. At all the hot-pressing temperatures, the SiC particles were tightly packed and the apparent grain growth occurred at 1900 °C.

Fig. 1 (a) Relative density and the decrease of specific surface area and (b) compressive strength for the SiC hot-pressed at 1400–1900 °C.

Fig. 2 Microstructures of SiC hot-pressed at 1400–1900 °C for 2 h.

3.2 Deformation behavior of SiC compact

Fig. 3 shows the typical relationship between compressive stress and strain for SiC hot-pressed at 1400–1900 °C. Fig. 3(a) and (b) shows the results parallel and perpendicular to the hot-pressing direction, respectively. The longitudinal strains (compressive strains) in both the directions were larger than the lateral strains (tensile strains). The non-linear deformation was sometimes observed in the porous SiC samples hot-pressed at 1400–1700 °C. A similar deformation was also observed in the porous alumina compacts in our previous study [11]. As seen in Fig. 3, the magnitude of the strain decreased as the densification proceeded. That is, the degree of deformation, especially in the longitudinal direction, became larger in the porous SiC compact.

Fig. 3 Relationship between compressive stress and strain for SiC hot-pressed at 1400–1900 °C. The compression direction is (a) parallel and (b) perpendicular to the hot-pressing direction.

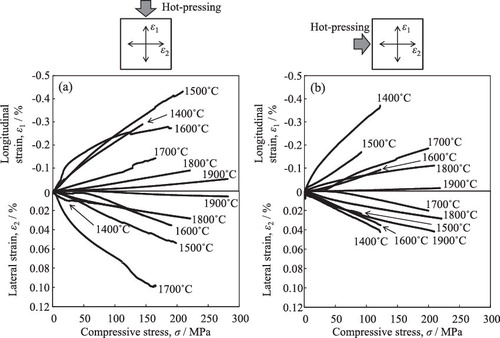
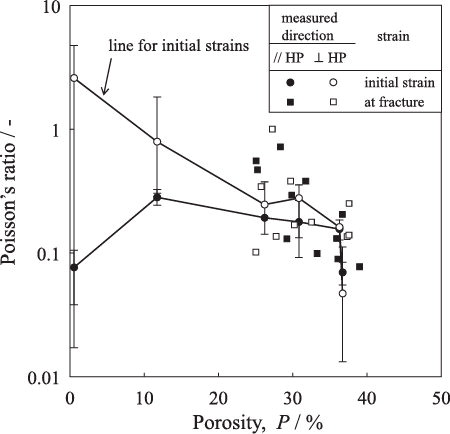
Fig. 4 shows the relationship between the strains at the compressive fracture and porosity of the SiC hot-pressed at 1400–1900 °C. In the SiC compacts with porosity smaller than 12%, the strains at the loading limitation of 6 kN are plotted because of no fracture. The longitudinal strains were in the range of 0.1–0.3% and increased at a higher porosity. Compared to the longitudinal strain, the lateral strains were not sensitive to the porosity and observed around 0.05%.

Fig. 4 Porosity dependence of strains at the compressive fracture of SiC. See Fig. 3 for the definition of longitudinal and lateral strains.

Fig. 5 shows the relationship between the Poisson's ratio (ɛ₂/ɛ₁ ratio) and porosity of the SiC hot-pressed at 1400–1900 °C. The Poisson's ratio was determined from (a) the initial strain range in Fig. 3 where the strain was proportional to the applied stress and (b) the strains at the compressive fracture. The Poisson's ratio measured in the hot-pressing direction was almost independent of the porosity but the Poisson's ratio measured perpendicular to hot-pressing direction increased at a lower porosity. This result was caused by a large lateral strain of dense SiC in the direction perpendicular to the hot-pressing direction shown in Fig. 3(b).

Fig. 5 Relationship between the Poisson's ratio and porosity of the SiC hot-pressed at 1400–1800 °C.

3.3 Young's modulus and compressive strength

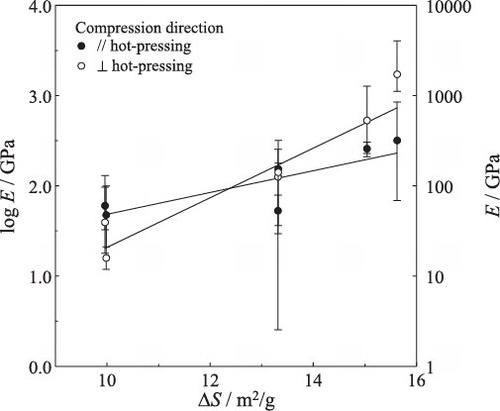
Fig. 6 shows the relationship between the Young's modulus and the decreased specific surface area (ΔS) due to the formation of grain boundary. The Young's modulus was determined in a small strain range where the strain was proportional to the applied stress. The Young's modulus increased with decreasing specific surface area of SiC. In the compression direction perpendicular to the hot-pressing direction, a significantly large Young's modulus (2570 ± 1460 GPa) was measured at ΔS = 15.6 m²/g (relative density 99.5%). The anisotropic Young's modulus is under investigation.

Fig. 6 Dependence of the Young's modulus on the decrease of specific surface area for the SiC hot-pressed at 1400–1900 °C.

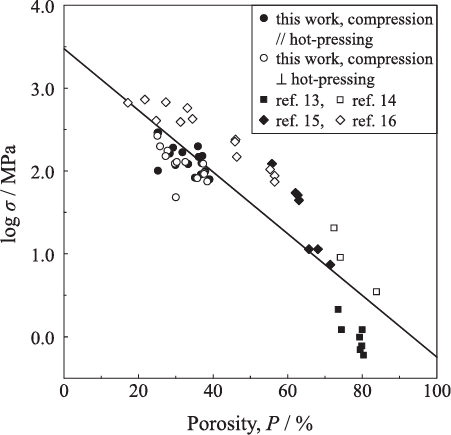
Fig. 7 shows the relationship between compressive strength and porosity of the porous SiC compact fabricated using a pore former (ex. polymer microsphere) at 1700–1950 °C in Refs. [13–16]. The porosity in Fig. 7 represents the total porosity of open pores and closed pores, and is close to the open porosity because of open porosity ≫ closed porosity. The pore structures of reported SiC compacts are characterized by bimodal pores of large pores (10–1000 μm diameter) corresponding to the pore former and small pores (<1 μm diameter) formed between SiC grains. The straight line for all the data was plotted according to Eq. (1)(1) $\sigma ={\sigma }_0\exp (-bP)$(1) by the least mean square method. Although the present SiC compacts formed significantly different pore structures compared to the reported porous microstructures, a similar compressive strength–porosity relation by Eq. (1)(1) $\sigma ={\sigma }_0\exp (-bP)$(1) was observed in Fig. 7. That is, the influence of pore size distribution on the compressive strength of porous SiC would be small. The reason is that the applied mechanical force is loaded on the grain boundary areas between adjacent SiC grains. The relationship between the compressive strength and grain boundary area is plotted in Fig. 8 and discussed in Section 3.4. The strength at 0% porosity in Fig. 7 was estimated to be 2.7 GPa, which was three times higher than the bending strength of 911 MPa of dense SiC in our previous paper [17].

Fig. 7 Relationship between compressive strength and porosity of porous SiC compacts.

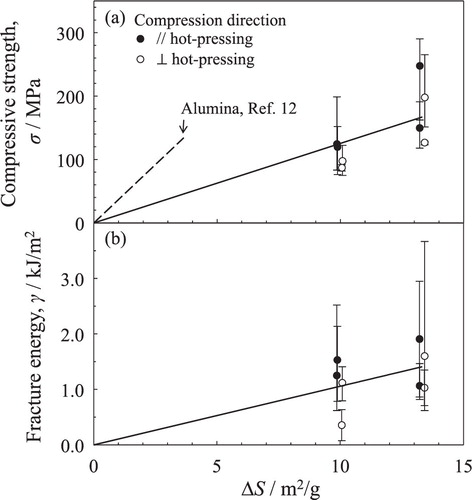
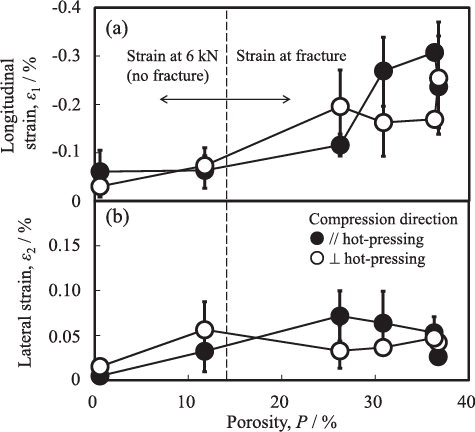
Fig. 8 shows the dependences of (a) compressive strength and (b) fracture energy (corresponding to the area surrounded by the stress–strain curve in Fig. 3) on the decrease of specific surface area for the SiC hot-pressed at 1400–1700 °C. Both the compressive strength (Fig. 1(b)) and fracture energy increased with decreasing specific surface area. Although the hot-pressing direction provided the larger strain than the direction perpendicular to the hot-pressing direction, a similar strength and a similar fracture energy were measured in both the directions, reflecting the influence of the Young's modulus in Fig. 6.

Fig. 8 Dependences of (a) compressive strength and (b) fracture energy on the decrease of specific surface area for the SiC hot-pressed at 1400–1700 °C.

3.4 Theoretical interpretation of compressive strength

In our previous paper, it was clarified that the compressive strength of porous alumina compact increased proportionally to the grain boundary area calculated from the decrease of specific surface area [11]. Hereafter we discuss again the compressive strength of a porous SiC compact based on the grain boundary area. Fig. 9 shows the relationship between relative density and shrinkage of SiC compact during the hot-pressing for the model structures with the particle coordination number of 6 (i.e. the simple cubic structure), 8 (body-centered structure) and 12 (close packing structure). The initial density (d₀) and the density (d) during hot-pressing of a SiC compact are related to the height (H) of consolidated compact by Eqs. (2)(2) $d_0=\frac{W}{H_{0}S}$(2) and (3)(3) $d=\frac{W}{HS}$(3) , respectively,(2) $d_0=\frac{W}{H_{0}S}$(2) (3) $d=\frac{W}{HS}$(3) where W and S are the weight of sample powder and the cross-sectional area of hot-pressing, respectively. The relative density (D = d/d_th, d_th: theoretical density) of SiC compact is related to the one-dimensional shrinkage (α = (H₀ − H)/H₀) and the initial relative density (D₀) of green SiC compact by Eq. (4)(4) $D=\frac{D_0}{1-\alpha }$(4) using the relationships of Eqs. (2)(2) $d_0=\frac{W}{H_{0}S}$(2) and (3)(3) $d=\frac{W}{HS}$(3) . In the cases of simple cubic, body-centered and close packing structures, D₀ values (i.e. the packing density of particles) are 52.4%, 68.0% and 74.1%, respectively:(4) $D=\frac{D_0}{1-\alpha }$(4)

Fig. 9 Relative density–shrinkage relation during hot-pressing of SiC compacts and for model structures of (a) close packing structure (coordination number of particles n = 12), (b) body-centered structure (n = 8) and (c) simple cubic structure (n = 6).

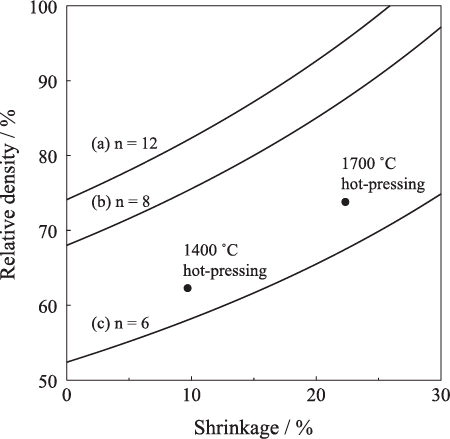
The measured data in Fig. 9 were close to the densification curve for a simple cubic structure. That is, the grain boundary area of SiC is discussed based on the simple cubic structure. The grain boundary area (A) for each grain is related to the decrease of surface area of starting SiC powder (ΔS m²/g) by Eq. (5)(5) $A=\frac{\Delta SW}{N}$(5) when the total grain number (N) in one SiC compact is kept to be a constant value during the initial sintering stage,(5) $A=\frac{\Delta SW}{N}$(5) where W is the mass of an SiC compact. The total number N is expressed by Eq. (6)(6) $N=\frac{W}{(4/3)\pi r_0^3\rho }$(6) ,(6) $N=\frac{W}{(4/3)\pi r_0^3\rho }$(6) where r₀ is the radius of starting SiC particles and ρ, the true density of SiC particles. That is, the coupling of Eqs. (5)(5) $A=\frac{\Delta SW}{N}$(5) and (6)(6) $N=\frac{W}{(4/3)\pi r_0^3\rho }$(6) provides Eq. (7)(7) $A=\frac{4}{3}\pi r_0^3\rho \Delta S$(7) :(7) $A=\frac{4}{3}\pi r_0^3\rho \Delta S$(7)

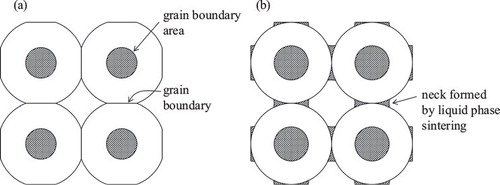
On the other hand, the number of grains (n) per unit area (m²) is given by Eq. (8)(8) $n={\left(\frac{N}{V}\right)}^{2/3}$(8) ,(8) $n={\left(\frac{N}{V}\right)}^{2/3}$(8) where V is the volume of SiC compact. Since the number of grain boundary per U m² of a compressive plane in a simple cubic structure is equal to the number of grains included in U m² (Fig. 10), the measured fracture strength (σ) is expressed by Eq. (9)(9) $\sigma =\frac{F}{U}=\frac{{\sigma }_{0}AnU}{U}={\sigma }_{0}An$(9) ,(9) $\sigma =\frac{F}{U}=\frac{{\sigma }_{0}AnU}{U}={\sigma }_{0}An$(9) where F is the applied load and σ₀ is the compressive fracture strength for dense SiC compact. The substitution of Eqs. (6)–(8) for Eq. (9)(9) $\sigma =\frac{F}{U}=\frac{{\sigma }_{0}AnU}{U}={\sigma }_{0}An$(9) results in Eq. (10)(10) $\sigma =\frac{4}{3}\pi r_0^3\rho \Delta S{\left(\frac{N}{V}\right)}^{2/3}{\sigma }_0=\frac{W\Delta S{\sigma }_0}{N^{1/3}{V}^{2/3}}$(10) :(10) $\sigma =\frac{4}{3}\pi r_0^3\rho \Delta S{\left(\frac{N}{V}\right)}^{2/3}{\sigma }_0=\frac{W\Delta S{\sigma }_0}{N^{1/3}{V}^{2/3}}$(10)

Fig. 10 Scheme showing (a) the grain boundary structure formed by solid state sintering (Al₂O₃ compact) and (b) the neck structure formed by liquid phase sintering (SiC compact).

Eq. (10)(10) $\sigma =\frac{4}{3}\pi r_0^3\rho \Delta S{\left(\frac{N}{V}\right)}^{2/3}{\sigma }_0=\frac{W\Delta S{\sigma }_0}{N^{1/3}{V}^{2/3}}$(10) indicates that the fracture strength increases linearly with increasing ΔS value at a same W/(N^1/3V^2/3) value. This model explains well the measured tendency in Fig. 8(a). The σ₀ value determined from the slop of linear approximation of the data in Fig. 8(a) was only 24 MPa and significantly lower than the compressive strength (2.7 GPa) at P = 0% in Fig. 7. In Fig. 8(a), the compressive strength of porous alumina compacts in Ref. [11] is also plotted as a reference. The σ₀ value (0.83 GPa) determined in the initial sintering stage of alumina compacts was 1/4–1/3 times of the compressive strength (2.2–3.3 GPa) of dense alumina compacts [11]. Fig. 10 shows the difference of grain boundary structures for (a) alumina by solid state sintering and (b) SiC by liquid phase sintering (dissolution–precipitation mechanism). The weak structure of a porous SiC compact as compared with the porous alumina compact would reflect the shear fracture during the deformation under compressive test. The shear strength of Si–Ti–C–O fabric/polytinanocarbosilane/mullite composites is reported to be 5–35 MPa [18]. These values are close to the σ₀ value of a porous SiC compact. Therefore, the deformation of porous alumina compacts (solid state sintering) under compressive test provides the strength of grain boundary formed perpendicular to the compressive direction. However, the compressive test of liquid phase-sintered SiC provides the strength related to the shear deformation.

4 Conclusions

The porosity of SiC compact with Al₂O₃–Y₂O₃ additives was controlled in the range of 0–40% by hot-pressing temperature (1400–1900 °C). Densification through a dissolution–precipitation mechanism of SiC was accompanied by the decrease in the specific surface area. The longitudinal strain at compressive fracture was in the range 0.1–0.3% and increased with increasing porosity. However, the lateral strain was independent of porosity and about 0.05%. The Poisson's ratio measured perpendicular to the hot-pressing direction increased with decreasing porosity. However, the Poisson's ratio measured parallel to the hot-pressing direction was almost independent of the porosity. The Young's modulus and compressive strength of SiC increased with decreasing specific surface area due to the formation of grain boundary. Although the Young's modulus and the strain at fracture depended on the measured directions, the fracture strength and fracture energy were almost independent of the measured directions. The compressive strength of a porous SiC compact increased with increasing grain boundary area. According to the theoretical modeling of the strength–grain boundary relation, the true compressive strength of dense SiC with no pores was calculated to be only 24 MPa. This value was about 1/100 times lower than the compressive strength (2.7 GPa) estimated for 0% porosity of SiC. It is interpreted that the grain boundary of liquid phase-sintered porous SiC is fractured by shear deformation under compressive test.

Notes

Peer review under responsibility of The Ceramic Society of Japan and the Korean Ceramic Society.